利用图卷积神经网络的道路网选取方法
2023-01-15朱余德晏雄锋
朱余德 杨 敏 晏雄锋
(1. 广东国地规划科技股份有限公司, 广东 广州 510650; 2. 武汉大学 资源与环境科学学院, 湖北 武汉 430079; 3. 同济大学 测绘与地理信息学院, 上海 200092)
0 引言
道路网是关键的基础地理数据,是交通、军事、经济等领域的重要研究对象。在多尺度地理数据库构建过程中,道路数量多、语义信息丰富、空间关系复杂,因此道路网综合一直是重要且复杂的问题。道路网综合包括目标选取和形状化简两个主要操作[1],目标选取是控制小比例尺地图上最终保留的道路目标,形状化简则是对保留目标进行形态上的简化处理。由于目标选取涉及多目标甚至全局目标之间关联关系的分析与判断,因此相对形状化简而言,往往更具难度。
道路网选取包括两个问题:选多少和选哪些。前者即数量控制,可通过开方根模型依据样图和制图经验,确定综合前后比例尺下较为合理的道路长度或数量保留比例[2]。后者即结构化选取,需要综合考虑道路目标的语义信息、几何结构、拓扑关系、空间分布以及关联要素等[3]。现有道路网选取方法主要以道路结点、弧段、网络或stroke为处理单元开展[4-5],其中stroke方法更关注道路之间的连通性,通过引入格式塔视觉感知中的良好连通性原则将一组连续性较好的道路弧段作为一个完整的处理单元,有效地兼顾了网络连接度、中心度等特征,还可以灵活地加入道路等级、类型等参量信息[2]。
机器学习方法被广泛用于道路网选取的自动化[6],例如,自组织映射[7]、神经网络[8]、本体知识推理[9]、遗传算法[10]等,这些方法改善了选取质量,但在特征表达能力上存在一定的局限性,可能对复杂道路网处理效果不佳。此外,传统机器学习方法不能直接自动提取道路的空间信息,依赖于专家知识建立道路选取的规则,例如,对长度大于给定阈值的道路予以保留[11],这一定程度上增加了选择过程的复杂性和主观性。近年来,深度学习得到了快速发展并逐渐成为遥感、制图等领域的重要组成部分[12-14]。深度学习通过多层神经元结构自动从数据中提取特征,相比传统机器学习具备了更强的特征挖掘和表征能力,且避免了人工特征提取,因此也被成功应用于地图综合,例如,建筑物综合[15]、道路模式识别[16]、形状表达与化简[17-19]等。本文将建立一种利用深度学习的道路网选取方法,利用道路网stroke模型构建图,利用图卷积神经网络(graph convolutional network, GCN)处理构建的图,并通过半监督学习方式预测节点的保留或删除状态实现道路网选取,以改进现有方法中特征表达能力有限以及过度依赖专家规则的不足。
1 方法
本文基本思想是将道路网选取问题转化为图节点的分类问题,即对输入道路网构建图结构,并通过GCN输出每个节点对应道路是否保留或删除,主要包括三部分:①stroke模型构建;②图模型构建;③GCN预测。
1.1 道路网stroke模型构建
道路网stroke模型构建即判断拓扑相连的弧段是否属于同一个stroke[2]。主要判断标准包括:①语义一致性,即道路属性(如名称、等级、车道数等)一致的相连弧段可判定为同一stroke,例如图1(a)中,弧段e1、e4、e5语义一致形成stroke。②几何一致性,夹角大于一定阈值的相连弧段被认为符合良好连通性原则,可判别为同一stroke。例如,图1(b)中,弧段e1和e3相交于结点P,相连直线段PA、PB形成的夹角α即弧段e1、e3的夹角。夹角越接近180°,弧段之间的延续性越强,其阈值取120 °~150°较为适宜。

(a)语义一致性

(b)几何一致性

(c)stroke模型图1 道路网stroke模型构建
上述两个标准中,语义一致性优先级较高,即语义一致的相连弧段在夹角不满足阈值条件下仍可判定为同一stroke。但考虑到数据库中语义信息的不完备性,仍需要结合几何一致性判断视觉上连通的弧段。对此,本文提出基于深度遍历搜索的stroke构建算法:①建立道路网的拓扑关系,并得到弧段集合E{e1,e2,…,en};②遍历E,计算其元素ei一侧的相连且不在集合E的弧段,如弧段数量≤1,判断是否符合几何一致性原则,符合将该弧段加入ei的stroke,并从E中剔除该弧段后返回,不符合则直接返回;如弧段数量>1,则按照语义一致性、几何一致性优先级,判断最符合连通性原则的弧段,加入ei的stroke,从E中剔除该弧段并以其为计算目标重复该步骤;③在ei一侧计算返回后,重复下一侧,直到集合E遍历完毕;④按照依据stroke连接关系将E中弧段分组,得到stroke集合S{s1,s2, …}。构建的stroke结果如图1(c)所示。
1.2 图模型构建
图是一种描述对象及其关系的数据结构,定义为G=(V,E,W),其中V={v0,v1,…,vn-1}是由n个节点构成的集合,E是连接节点的边的集合,W是n×n的邻接矩阵,表示每对节点之间的边的权重,如果节点之间存在边,则权重为1,否则为0。邻接矩阵W的拉普拉斯矩阵L定义为L=D-W,其中D为节点度di构成的对角矩阵D=diag(d0,d1,…,dn-1)。每个节点可包含一个或多个特征,组成n×m的特征矩阵f表示定义在图上的函数,其中m为特征数量。
本文以stroke为节点、stroke之间的空间相连关系为边构建图,如图2所示。该方法可以充分利用stroke增强弧段之间的连通性,例如一个stroke可能与数十个stroke相连,而道路节点或弧段最多存在数个节点或弧段相连,这种高连通度可以提升道路网信息之间的传递。

图2 针对道路stroke的图模型构建

1.3 GCN模型
本文利用半监督学习的GCN模型处理上述构建的图实现道路网选取。GCN模型采用分层设计思想[20],除输入层和输出层外,还包含两个卷积层。输入即拉普拉斯矩阵L以及节点特征矩阵f。卷积层即利用多个卷积核对上一层信息进行处理,每一个卷积核处理后得到一个新特征,多个卷积核组成一个完整的卷积层。整体架构如图3所示。
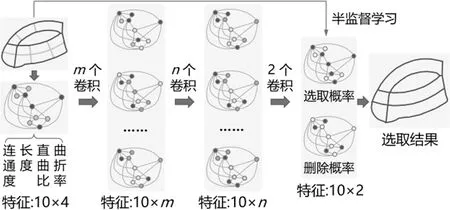
图3 利用半监督图卷积神经网络模型的道路网选取
卷积层之间的运算通过基于傅里叶变换的图卷积完成[18,20],消息传递过程为
(1)

以图3架构为例,输入特征f经m个卷积核运算后得到12×m维特征向量的特征层,m即新一层的节点特征维度,即图的数量。多次卷积后,最后一个卷积层中使用两个卷积核,以输出12×2维特征向量分别表示12个节点保留或者删除的预测值。如果某一节点保留的概率大于舍弃的概率,则对应stroke将保留;否则,将被删除。
半监督学习方法被用于训练GCN模型,即随机挑选一部分节点进行标注,标签值y为 [1, 0]或[0, 1],分别表示保留或删除该节点对应的stroke。训练时,模型处理后输出每一个节点的状态预测值Z=[z1,z2],利用交叉熵计算随机挑选出的部分节点的预测值和标签值之间的差异。由于每次预测时,全部的节点特征是作为整体输出的,通过最小化这部分节点的特征可以不断优化模型,最终其他节点的特征也将借助节点之间的空间关系得到优化。
2 实验分析
实验数据选自中国西部地区1∶10 000比例尺数据,包括3 624条道路,总长度1 390 km。首先对数据进行相交打断、断线及悬挂线连接等预处理,以保证拓扑正确性。构建stroke时,为了避免冗余节点干扰弧段夹角的计算,所有道路采用阈值为5 m的道格拉斯算法处理;夹角阈值设置为150°,最终得到1 317个stroke。计算每个stroke的四个指标作为图节点特征,并用Z-score方法归一化每个特征。GCN模型包含两层128个卷积核的卷积层,考虑到stroke连通性强,卷积核阶数设为2;模型学习率、dropout值、训练最大次数分别为0.000 2、0.2、20 000。随机选择25%的道路stroke作为训练数据,并设置60%和30%两个选取比例,结果如图4所示。

(a)选取60%

(b)选取30%图4 道路网选取结果
可以看到:①模型在不同选取比例下都能较好地保留等级较高、长度较长的stroke;②尽管是图节点级的预测,但道路连通性整体上保持得较好,这得益于stroke连接关系的有效利用;③在一些较密集的区域,如城市街道,删除的道路弧段较多,而道路较为稀少的区域,如郊区道路,删除的道路弧段较少,密度保持较为稳定变化。总体而言,选取结果总体上是符合预期的。
为了详细分析提出方法的优劣,本文与人工选取结果进行对比,该结果由两名具备专业知识的人员相互独立完成并交叉验证后得到,对比结果见表1。可以看到,GCN与手工选取结果的一致性占比分别为84.7%和79%。GCN在两个选取比例下保留的道路长度均略长于人工选取的道路长度,这表明GCN方法趋向于保留较长的stroke,可能原因是考虑了stroke长度特征,并且对于较长的stroke,其连通度一般也较大,因此在选取时呈现较强的保留趋势。手工选取时,考虑到连通性要求,对较短的stroke保留得较多。此外,GCN选取与人工选取也存在一些不一致,人工选取针对农村形态弯曲的道路形成了延展性更强的道路连接关系,而GCN对这种连通性特征考虑较少。

表1 GCN方法与手工选取的结果对比
道路分布密度保持是选取质量评估的重要因素。为了定量化选取前后的密度变化,本文采用格网化分析方法,将实验区域均匀划分为20×20的网格,并计算每个格网内道路的长度,通过最大最小方法均一化得到密度分布图;进一步,计算每个格网选取前后密度的差值,并取全部格网密度差的平均值作为整体密度变化指标(density change, DC),计算为
(2)

本文选取前后的密度分布如图5所示,变化情况见表2。当选取60%时,密度总体变化不大,D值为0.051,优于人工选取;右侧是城市街道区域,道路分布较为稠密,选取后仍然保持较高的密度分布;整体的连续性分布保持也和原始密度图较为一致。当选取30%时,D值为0.12,略高于人工选取;左侧出现了较大区域的低密度区域,与原始密度图差异较大,表明该区域的道路被删除较多,分析原因可能是农村道路弯曲多样、形态复杂,基于局部几何关系分析的连通性交叉,因此构建的stroke较短,在保留被予以删除。

(a)选取前

(b)选取60%

(c)选取30%图5 道路网选取前后密度图

表2 选取后道路整体密度变化情况
3 结束语
本文提出一种stroke模型和GCN模型支持下的道路网自动选取方法。该方法以stroke为图节点、stroke间的连接关系为图的边构建道路网的图结构,并利用GCN模型通过半监督学习方式预测节点的保留或删除状态,实现道路网选取。实验表明,该方法能得到整体上与人工选取较为一致的多尺度道路网选取结果,能有效地保持局部道路的连接性以及整体的密度分布特征。该方法保留较小比例道路时,农村地区复杂弯曲道路相较人工选取结果删除稍微偏多,该问题可以考虑通过采用更完备的stroke构建指标形成延展性更强的道路连接关系予以改进。
