除臭通风空间负压分析模拟

屈志敏，吕蒙

（中城院（北京）环境科技有限公司，北京 100120)

1 引言

近年来，在国家碳中和及碳达峰的“双碳”目标背景下，环保要求同步提高。有机垃圾处理厂作为重要的大气污染物排放源，其除臭系统近年来规模大幅提高。除臭规模的增加一定程度上能够提高除臭效果，但也带来了高能耗，这与节能减碳的目标背道而驰。在保证除臭效果的基本前提下，降低除臭系统规模，减小除臭系统能耗是有机垃圾处理厂除臭系统面临的一个重要现实问题。

计算流体动力学（Computational Fluid Dynamics,CFD）已经被普遍作为科学研究和工程设计中有力的预测仿真工具，可以用来研究通风房间的气流组织和负压度等。

本文通过对通风房间进行CFD仿真模拟，在排风口风量及风速一定的条件下，用3种不同大小的自然补风口模拟维护结构缝隙不同的漏风面积，通过这3种典型模拟，探讨不同的漏风面积对室内负压度的影响。同时利用理想流体伯努利方程来计算理论负压，另外参考GB 50073—2013《洁净厂房设计规范》中给出的工程经验算法，来确定相同条件下的经验负压，对比上述3种方式得出的负压结果，确定能够应用于实际工程设计中比较有效简便的负压计算的工程应用方法，从而对有机垃圾处理厂除臭系统规模的确定提供技术支撑。

2 通风房间模型描述

2.1 物理模型及初始条件

本文主要研究的是除臭通风车间内，在一定除臭排风量的条件下，补风口或者维护结构漏风面积大小对车间内负压度的影响。为节省算力资源，提高计算精度，通风车间选用一个小型通风房间进行研究，该通风房间基本尺寸为7 m（长）×5 m（宽）×3 m（高）。通风形式为机械排风，自然补风。排风口设置在屋顶，维护结构漏风设置为补风口设置在两侧墙体下沿距地0.2 m。其中，排风口尺寸为0.18 m×0.2 m，排风口面积0.036 m2。自然补风口设置3种工况，分别为补风口总面积0.2 m2、0.1 m2、0.05 m2，如图1所示对应3种模型。

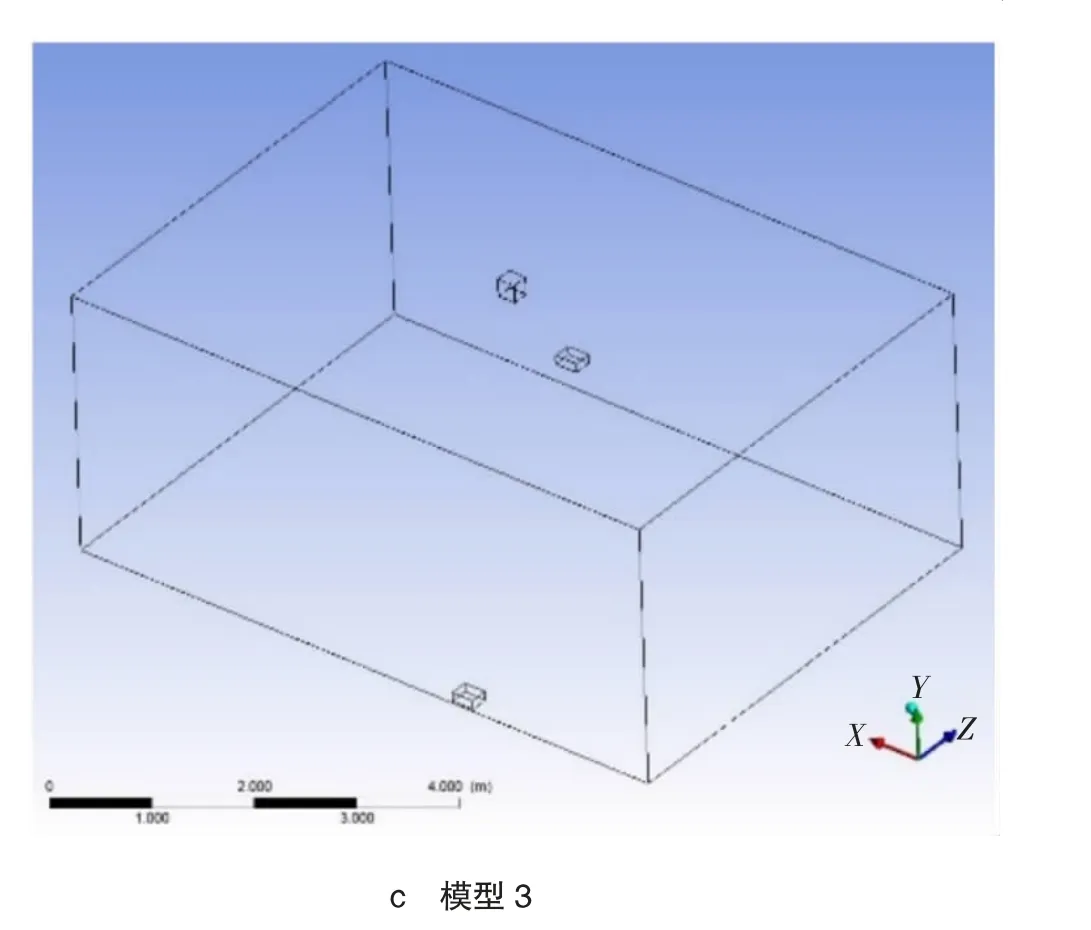
图1 3种通风模型三维结构示意图

房间机械排风量为5次换气/h，计算排风量为525 m3/h，3种模型对应排风口及补风口面积与风速如表1所列。

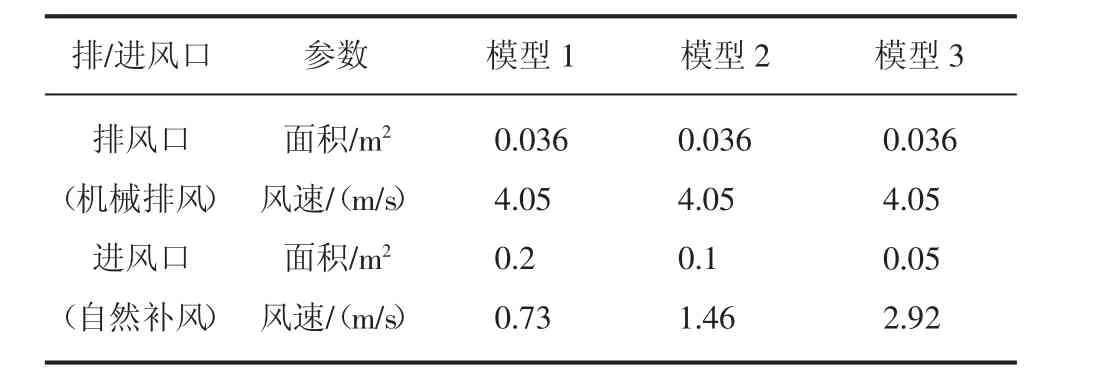
表1 物理模型初始条件表

2.2 假设条件及理论基础

2.2.1 假设条件

为简化数值模拟计算，需要进行如下合理假设条件：

1）温度对负压研究无影响，故假设进排风均为等温射流。

2）辐射换热对负压研究无影响，不考虑辐射换热。

3）流体按流动参数是否随时间变化分为定常流动和非定常流动，模拟室内空气稳态流动，为减少计算因子，将室内空气假定为定常流动。

4）流体分为可压缩流体及不可压缩流体两种，空气作为一种可压缩流体，由于压强研究范围仅在0～50 Pa，空气分子的可压缩性对负压度的研究影响可忽略，为简化连续性方程，不考虑空气密度的影响，假定室内空气为不可压缩流体。

2.2.2 理论计算方程

1）连续性方程

流体为定常流动，不考虑时间因子的影响：

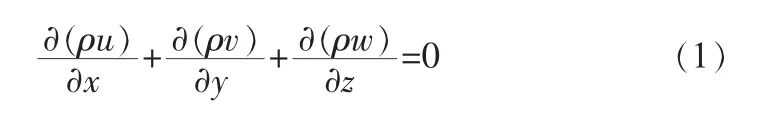
式中，u、v、w分别为流体微元在3个方向x、y、z的速度；ρ为流体密度。

不考虑流体密度的变化，流体假定为不可压缩流体，则连续性方程可得到进一步简化：

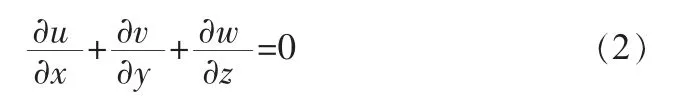
2）动量方程

根据动量定理，流体系统流动的时间变化率等于作用在系统上的外力矢量和，即：

式中，m为流体质量；V1、V2分别为t1、t2时刻的流体速度；Δt=t2-t1。

根据不可压缩流体一维流动连续性方程，流体在总流进出口的流量相等，可得出不可压缩流体定常流动的一维流动动量方程：

式中，qv为流体体积。

三维定常流体的动量方程即：

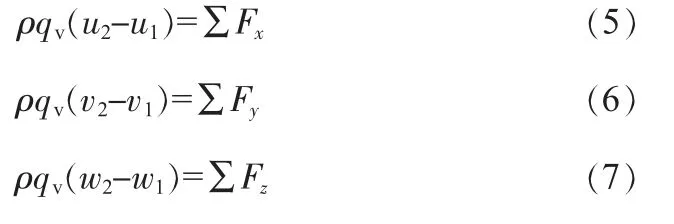
3 模拟条件及结果

3.1 模拟条件

3.1.1 计算模型

机械通风空气为高雷诺数湍流流动，适用k-epsilon标准模型，壁面选择标准壁面函数。重点研究通风量对负压度的影响，不考虑辐射换热与温度对空气流场的影响。

3.1.2 边界条件

壁面选择气流无滑移静止壁面，不考虑壁面粗糙度影响。机械排风口设置为速度入口，速度为-4.05 m/s，自然补风口设置为压力出口。 赵福云[1]、赵斌[2]、凌继红[3]等通过理论计算、相关实验与验证均认为湍流强度对室内空气流动的影响可忽略，故不考虑湍流强度对气流出入口的影响。模型中速度入口与压力出口湍流强度均设置为4%，回流水力直径0.5 m。

3.1.3 求解方法

气流组织分析一般采用SIMPLE方法，采用压力与速度相互校正强制质量守恒并获取压力场。PISO方法适用于过渡计算和高度倾斜网格计算，不适用于本次数值模拟。SIMPLEC方法虽然能够更快得到收敛结果，但容易产生不稳定。另外一种算法为耦合求解，更合适用于高速可压缩流动，不适用于本次数值模拟。

3.1.4 初始化

本次数值模拟的对象为通风房间空气流动，为单相流体，采用混合初始化求解。

3.2 模拟结果分析

对上述模型进行迭代求解，可以直观得到室内气流组织速度流场，具体速度场模拟结果如图2所示。

如图2所示，最大风速在排风口中心处约5 m/s作用，排风口初始条件4.05 m/s为风口平均速度。自然补风口模型1到模型3的补风口面积逐步减小，在此基础上，模拟计算空间负压，计算结果如图3所示。

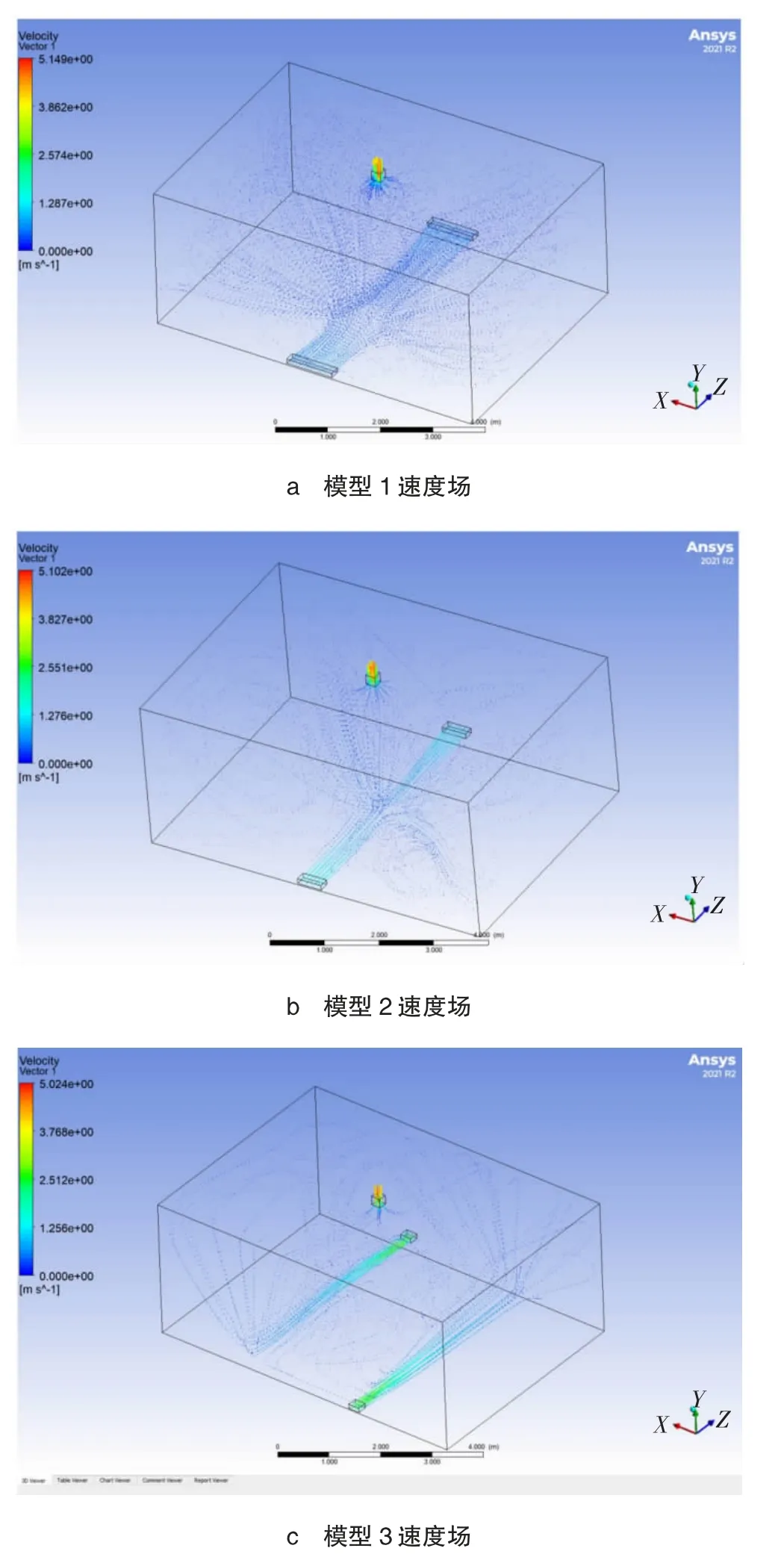
图2 3种模型速度场示意图

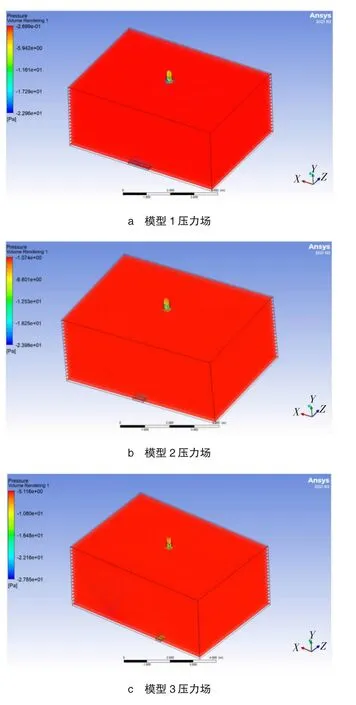
图3 3种模型压力场示意图

如压力场模拟计算结果所示，模型1模拟负压结果为-0.27 Pa，模型2模拟负压结果为-1.07 Pa，模型2模拟负压结果为-5.12 Pa。

综合模拟初始条件排风口面积一致条件下的数据结果对比，如表2所示。

表2 数值模拟结果分析表

从表2结果分析可知，随着进风口面积的减小，进风口风速逐渐增加，负压度也相应增加。且增加幅度远大于进风口风速增幅。故而可以认为维护结构的密闭性对通风房间负压度起到决定性影响。

4 其他方法负压计算分析

4.1 理论负压计算分析

在计算流体动力学中，理想流体的运动微分方程在假定流体为不可压缩理想流体的定常流动，质量力只有重力作用，且沿同一微元流束积分的假定简化条件下，得到理想流体微元流束的伯努利方程[4]：

式中，z0、z1为单位重力流体的位势能；p0/ρg、p1/ρg为单位重力流体的压强势能；V02/2g、V12/2g为单位重力流体的动能。

将入口通风气流段看作微元流束，室外大气看作流束入口，房间内气流入口看作流束出口，室内空间负压度为相对压力，故室外压力即流束入口压力取值为0 Pa，室外空气作为流束入口风速为0 m/s，流束出口压力即室内负压，流束出口流速即房间气流入口风速。忽略位势能的影响，可以简化计算室内负压与气流出口风速之间的数值关系，伯努利方程可以改进得出：

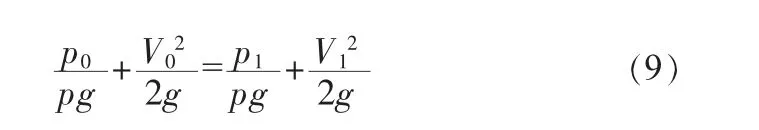
式中，p0为大气压力，取值0 Pa；V0为室外空气风速，取值0 m/s；V1为气流出口风速，m/s；p1为房间负压值，Pa；ρ为常压下空气密度，取值1.2 kg/m3；g为重力加速度，取9.81 m2/s。

可以得流束出口风速与房间负压值的关系式如式（10）：

代入3种模型的初始条件，对比模拟计算结果分析见表3。

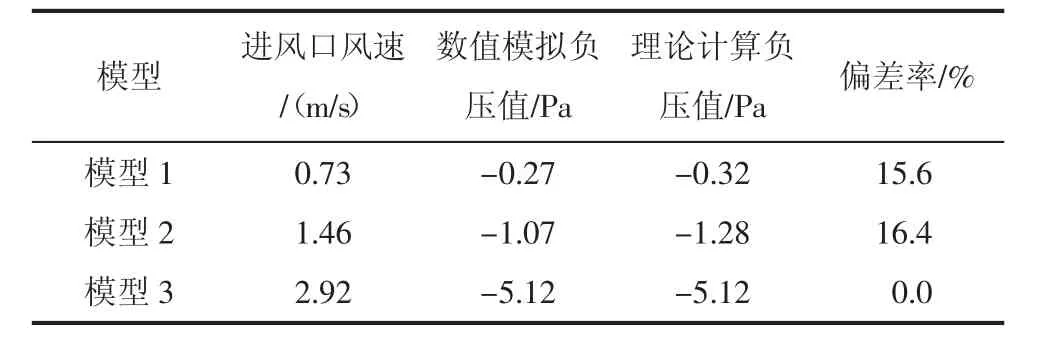
表3 数值模拟与理论计算对比分析表

上述结果表明，运用简化的理想流体伯努利方程来计算负压值，与数值模拟结果的偏差率在15%左右，且理论计算结果小于数值模拟负压值结果。

4.2 经验负压计算分析

在GB 50037—2013《洁净厂房设计规范》[5]中，有关洁净区与周围空间需要维持一定压差的规定，给出了缝隙法计算维持洁净室压差值所需的压差风量。对非密闭门试验数据进行分析，如表4所示。

表4 非密闭门漏风量试验数据

洁净室非密闭门缝隙按1.6 mm验算压差与漏风量之间的关系，可以验算得出压差与漏风量满足上述理论计算式。

5 数值模拟与其他计算方法结果对比分析

5.1 室内负压度的影响因素

经前述数值模拟可以看出，设有机械排风的除臭通风房间，负压度主要与维护结构的开口面积大小有关，且开口面积的大小对负压度的影响相当明显。模型1～模型3的3种模型压力场显示，室内负压度均匀，室内负压度与缝隙所在位置无关，即气流组织不影响室内负压度。

5.2 室内负压值的确定

通过数值模拟得出的进风口风速与负压值的关系，结合简化的理想流体微元流束的伯努利方程，在理论计算的基础上附加一定的系数来契合模拟结果，能够作为一种更简单的工程实际应用的计算方法。

实际工程中需要用负压值来控制通风量，为保证负压效果，采用理论计算值直接作为估算除臭通风风量是可行的。通过模拟数值来看，其结果相当于在维持一定负压的条件下所需的实际除臭风量的基础上附加了15%，这在实际工程中作为常用的保证系数具有可靠性。

6 结论

1）除臭通风车间负压值在除臭风量一定的条件下，仅与维护结构漏风面积相关。漏风面积越大，室内负压程度越小，越不利于室内污染物的外溢控制。室内负压度与渗漏风口的风速直接相关，数值关系对应简化的微元流体伯努利方程。

2）工程设计应用中，可以采用两种方法来确定室内除臭风量。其一，确定常用不同类型的门窗及维护结构缝隙宽度值，通过缝隙长度估算维护结构漏风面积，进而通过所需控制的室内负压值计算进风风速，从而确定除臭通风风量。其二，确定不同类型的门窗及维护结构单位长度缝隙在维持一定压差条件下所需的压差风量，从而估算除臭通风风量。这两种方法均有前置条件，也是在今后的工作中需要进一步调研与研究的重要内容。

3）有机垃圾处理厂作为重要的污染排放源，如何有效控制污染物的扩散外溢以及降低控制成本，是一个具有相当现实意义的问题。强化围护结构的密闭性，能够有效降低除臭系统初投资成本及运营成本。投资成本与节能减碳的经济效益的平衡，也是今后工作中需要进一步研究分析的问题，这对于指导工程建设实施，充分响应国家“双碳”目标具有重要的现实意义。