基于CAPM模型对互联网金融板块的实证分析

徐争荣　韩星灿

摘 要：随着互联网技术的快速发展，互联网金融行业也迅速发展壮大，互联网金融自身所具有的优势必将对传统的商业银行间的竞争和经营行为带来巨大的影响。为进一步验证资本资产定价模型在股票市场的有效性，选取互联网金融行业的股票，利用其在2015年12月31日—2020年12月31日的月交易数据进行实证研究分析。利用统计学相关软件进行回归检验，验证CAPM模型在互联网金融板块的适用性，得出结论并给出建议。

关键词：资本资产定价模型；互联网金融；适用性；实证检验

一、引言

互联网技术不断创新、深化发展，在不断地促进金融业的发展。互联网金融很好地实现了互联网科技与金融业的结合，不但方便快捷而且普惠性较强、成本也低，从而可以提高资源配置的效率，促进中小型企业的发展，增加就业机会。互联网金融的发展对我国经济的稳定健康运行产生了重要的影响。但是出于规避风险的考虑，也为了更好地服务消费群众，继续推进金融改革与技术创新是必须完成的任务。

资本资产定价模型（Capital Asset Pricing Model，CAPM）是现代社会中金融研究发展的基石，其在经济的理论发展中具有重要的意义。从资本资产定价模型的理论内涵看，其以一种简单的线性模型揭示了资产的收益与风险之间的均衡关系。从方法论角度来看，CAPM模型基于对投资者和市场的一系列假设，通过严谨的理论推导，得到了资产与资产组合的风险收益均衡关系。尽管CAPM模型的结论在许多情况下与实证检验的结果不一致，但由于其应用简单和精准度高等优点，在许多重要实践中仍被广泛应用。

多年以来，许多学者对CAPM模型在我国股市中的有效性进行了实证分析和理论研究，对我国股市的发展起到了一定的推动作用。因此本文旨在运用CAPM模型对我国互联网金融板块的股票进行实证检验，并探究其有效性。基于此，为该模型的适用和其行业的发展提出一些建议措施，以期促进行业稳定健康发展，营造安全稳定的金融环境。

二、文献综述

对CAPM模型的研究最早始于国外，自20世纪70年代，国外学者就开展了大量的实践研究，其中，Black et al为了验证模型的有效性，将选取的数据以时间序列的方式进行了检验。他们发现，股票的收益率水平与β系数之间有正相关的线性关系。他们的实验不仅得到了这个结论，还发现了非系统性风险在其中发挥的作用。

随后，Fama和Macbeth也对CAPM模型开展研究，他们利用多元线性回归的方法发现了收益率与β系数间具有的关系，即呈现出正相关线性关系，却并没有发现Black等得到的额外结论。Fama和French的研究更使人信服，他们使用数据将股票按照财务能力和规模进行了分类，然后在每组中按照β值大小再次分成小组，却无法发现两者变量之间的相关关系。他们又在分析指标中加入了公司规模情况，经过实证分析，发现公司状况和市场收益基本能够解释股票收益率的变化，而β系数并不能很好地解释股票的报酬率。

中国证券期货2022年9月

第3期基于CAPM模型对互联网金融板块的实证分析

对CAPM模型的研究中，我国学者也发挥了难以忽视的作用。最早的研究起始于施東晖所做的实验，他整理了沪市1993年4月到1996年5月50只股票的历史收盘价数据，经过大量分析后认为，股票的收益率与系统风险之间没有显著关系，却发现非系统风险对股票收益率发挥了非常重要的作用。经过实验的论证，得出理论上的资本资产定价模型并不适用于我国实际的证券市场情况，甚至产生相反的结论。换言之，我国证券市场的运行中，系统性风险占比过高，非系统风险占比较低，投资者几乎不能通过分散投资来规避风险。

陈小悦和孙爱军运用根据财务规模进行分类分组的方式对我国证券市场的收益状况进行了实验分析，在控制好一定的规模后，得出结论：β系数不能准确合适地解释股票收益状况，从而得出资产定价模型在我国股票市场并不适用的结论。而孙鹏飞等进行的研究证明，在股票市场中，并不是只有系统风险这一个决定收益的因素存在，成交量、财务规模、流通比率也会影响股票的收益率情况。

此外，杨朝军和邢靖也针对CAPM模型的检验做了相关实验，认为若在CAPM模型中加入其他影响股票的因素，可能会对模型有更好的解释。他们在上海股票市场中选取了时间跨度为3年期的所有A股股票，通过传统的CAPM模型检验和加入其他可能影响股票收益的因素形成的CAPM模型进行检验，结果说明，与传统的CAPM理论模型并不一致，在沪市股票市场中不仅有系统风险可以决定股票收益率，还有财务规模、流通比率等指标也会影响股票的收益率水平，并且由于时间在变动，各因素对收益的影响程度也在变动。高永涛和牟新建两位经济学家将招商银行和上海浦东发展银行作为实验对象进行分析，得出的实验结果表明，CAPM模型现在还不能够完全适用于我国证券市场，从侧面也说明，目前我国的证券市场发展不够成熟。

三、模型简介及数据变量选取

（一）CAPM模型简介

CAPM模型围绕资本市场发展理论来研究在证券市场中股票的预期收益率与风险之间的关系。无风险利率条件下CAPM模型的标准形式如下：

E（rp）-rf=α+βim［E（rm）-rf］

式中，E（rp）为资产在t时期的期望收益率；E（rm）表示市场组合的收益率；rf为无风险收益率；βim为资产对应的β系数；α为截距项，即定价的误差项。

CAPM模型要想实现，需要的假设条件如下：

（1）在一个投资周期内，评估投资组合的价值需要用到股票收益率与标准差两个指标。

（2）收益率越高，投资者选择机会越大。

（3）标准差越低，投资者选择机会越大。

（4）投资者可以任意决定买卖资产或者组合的任何部分。

（5）不考虑税收政策和任何可能出现的交易费用，模型理想化。

（6）投资者获得和使用的外部信息是相同的即每个人投资时间相等，无风险利率相等。

（7）不论哪种资产，不同投资者对同一资产的预期收益与风险状况都有同一预期。

基于这些假设，资产定价模型假设现实生活中投资的行为是这样的：每个人都了解相同的信息，具有相同的处理问题的能力，对证券有一致的了解；证券市场是一个完整的市场，不妨碍投资。通过观察市场中所有投资者的统一的行为方式，可以得到证券的风险与收益率均衡关系的特点。

（二）数据的来源与选取

本文以没有违规行为及剔除ST股票等为筛选条件，从体现样本数据选择的普遍性与适用性的角度，利用Choice金融终端从上海证券市场互联网金融板块中选取了30只股票。包括重庆百货、栖霞建设、安源煤业、雅戈尔、高伟达、三联虹普、赢时胜、三六五网、拓尔思、鸿利智汇、派生科技、数码视讯、金财互联、华斯股份、大金重工、中粮资本、大北农、千方科技、海宁皮城、罗莱生活、世联行、久其软件，凌志软件、生意宝、恒生电子、安硕信息、指南针、大智慧、神州信息、同花顺。时间跨度为2015年12月31日到2020年12月31日。

鉴于时间跨度较长，从2015年12月31日到2020年12月31日为期5年，如果把日作为分析周期，中间可能因为某个事件出现股价异常。为避免出现不实际或者没有意义的结论，本文采用月度数据作为分析周期进行实证检验。数据来源于Choice金融终端，收益率按每股月末最后-交易日收盘价计算。同时，为了避免股利分配的偏差，本文选择了经过前复权的月收盘价。

运用Excel软件对数据进行初步处理，将原始股票的当月收盘价减去上一月度收盘价之后再除以上一月度收盘价，用这一方式计算股票的期望收益率。

（三）模型变量的设定

1.无风险利率

本文所用到的无风险收益率数据来自我国金融机构一年期存款基准利率，该指标在2016—2020年基本维持在1.5%，即年无风险收益率是1.5%，则月无风险利率为0.125%，认定该数据为所需指标数值。

2.市场收益率

上证综指可以准确地反映股市的发展趋势，具有良好的市场代表性，作为一种价值加权指数，也符合CAPM模型关于市场组合在结构上的要求。并且由于选取的30只个股样本均在沪市进行交易，因此，市场收益率便用上证综指的股票收益率情况来表示，计算出其月度收益率。记E（rm）为t时的市场组合收益率。

四、CAPM模型回归分析

对CAPM模型的回归分析主要体现在对检验的结果中三个方面进行分析：回归直线方程的截距项是否为0；β系数是否为1，是否可以体现投资组合与市场组合收益变动情况；市场组合的风险溢价数值是否为正。

在进行回归分析之前，首先构建资产组合的时间序列并计算收益率，在对股票市场研究的基础上，将选取的30只股票通过随机抽样的方式分为5组，每组6只股票，投资组合的期望收益率采用单个组合期望收益率的等权重均值，即用计算平均值的方法分别计算6只股票的平均数来代表投资组合的收益率。

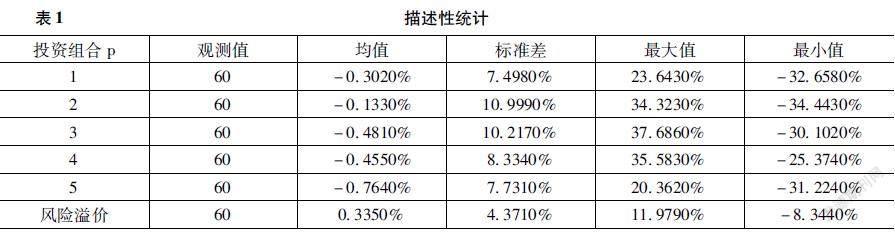
（一）描述性统计

用Excel软件对投资组合进行描述性统计统计结果如表1所示。投资组合与风险溢价的观测数据均为60个数据，投资组合均值较低，基本为负数，表示选取的互联网金融板块的股票收益率大多数会比无风险收益率要低，收益较小；而风险溢价基本大于0，认为市场组合的收益率基本是高于无风险收益率的，满足了CAPM模型的检验条件；各个投资组合的标准差相差无几但都大于风险溢价的标准差，说明数据组合没有上证综指的收益率稳定，数据组合会有较大差别。同时，投资组合的最大值均比风险溢价大，最小值均比风险溢价小，说明各个组合内单只股票收益率数据变化较大。

（二）单位根检验

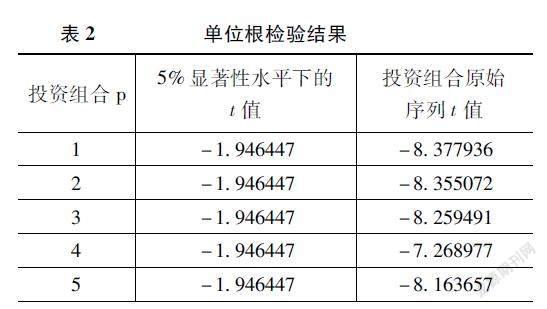
通过Eviews软件对每个投资组合的收益率数据进行ADF检验即单位根检验。检验其序列是否为平稳序列，這是进行实证研究的前提。单位根检验结果如表2所示。

用Eviews软件进行ADF检验，通过上述实验结果我们可以得到，组合原始序列的t值均小于在5%显著性水平条件下所对应的t值，则通过检验，应该拒绝原假设，认为该序列为平稳序列，并不存在单位根。

（三）最小二乘法检验

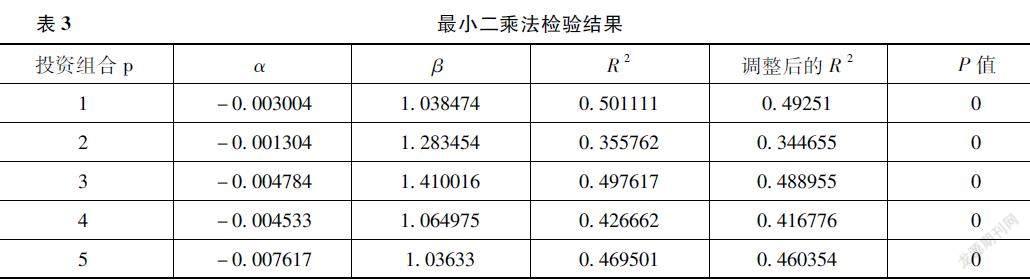
本文通过对5组月平均期望收益率的数据运用最小二乘法方法进行回归分析，可得各组的β系数以及R2、P值等情况。回归结果如表3所示。

回归系数的显著性检验：对以上实验所得出的结果进行分析，这5个股票组合检验出的β系数的P值均为0，比显著性水平0.05小，要拒绝原假设，β系数很明显不为0；检验结果中5个投资组合的β值均大于1，但接近于1，可以认为各个投资组合的收益率变动与市场组合的收益率变动趋于一致，则解释变量对被解释变量的影响显著，也能够得出互联网金融板块股票收益率与上证指数收益率存在显著线性相关关系，其收益率显著受市场的影响。

可决系数R2：R2的数据显示出系统性风险在总风险中所占的比例。根据上面回归结果可以知道，5个投资组合中只有1个投资组合的R2大于0.5，剩下的R2数值都稍微小于0.5，在0.4附近徘徊，可决系数稍低，最低的可决系数为0.355762，而大于0.5的也仅有0.501111。实证检验的结果可以说明该方程整体的拟合优度较差，β系数并不能较好地表示出两变量之间的线性关系，同时这表明β系数并不能有效地解释出互联网金融行业股票收益率的变化，这进一步表明除系统性风险外，依然存在着其他影响互联网金融板块股票收益率的因素。

对截距项α的分析：α不等于0意味着市场中存在着不完全均衡的定价。由以上研究结果可得，5个投资组合的截距项都在-0.005左右，数值不大，可以看出互联网金融板块的市场基本均衡。

（四）稳定性检验

为了检验本文采用的模型的稳定性，本文将改变分组的方式来进行稳定性检验。将之前随机抽样的方式分成5组改变分组方式，仍然是6只股票，再进行一遍CAPM模型回归分析，单位根检验最小乘法检验。结果证明模型可靠、检验结果依然显著，模型具有稳定性。

通过以上回归检验，可以总结出以下实验结果：首先选取的数据序列经过单位根检验证实为平稳序列，这是进行实验的前提。然后通过最小二乘法回归检验分析，回归直线方程的截距项基本在0，则表示出互联网金融板块的市场基本均衡；在显著性水平0.05的条件下，投资组合的β系数很明显接近于1，表现出变量之间显著的线性关系，也表现出互联网金融板块股票收益率与市场组合收益率的变动趋于一致，β系数也表达出系统性风险的经济含义，表明系统性风险对资产定价的影响程度；而R2数值在0.5左右表明回归直线的拟合优度整体较差，说明自变量对因变量的解释力度不大，β系数并不能很好地描述它们之间的线性关系，除系统性风险会对收益产生影响外，还存在其他影响因变量的因素。

五、结论与建议

本文通过对互联网金融板块的股票进行CAPM模型的实证分析，现阶段β系数对我国互联网金融板块股票收益率与资本定价的解释还不充分，存在除此之外其他影响收益率的因素。目前的实证显示当前的CAPM模型并不适合对我国互联网金融业进行分析。CAPM模型作为一个理想模型，对假设有着严格要求，这与我国股票市场的现状出入较大。我国互联网金融行业的价格波动剧烈，目前的情况还远远不是理论上所要求的条件。因此，CAPM模型在实际应用过程中存在很大的局限性，包括我国互联网金融市场的发展，反映出其还不够成熟的状况。因此，当前的CAPM模型并不适用于分析我国互联网金融板块股票的收益率情况。

传统的CAPM模型假设太过理想化，很多条件在实际的市场中几乎不能得到满足，同时我国证券市场发展相对较慢，互联网金融板块的价格波动较大，当前证券市场不成熟的发展现状与模型严格的理论要求相差较大。我国股票市场的信息披露不完全，或者投资者结构不合理这些因素都影响着CAPM发挥实际作用，这也导致了模型的回归结果没有得出理想的结论。然而，事实上理想的、完全符合CAPM假设的市场也是不存在的，我们所能做到的只是使实验的条件尽可能地接近理想条件，但不能达到完全的等同。因此在实际模型的运用过程中，CAPM模型存在着很多局限性。

因此，本文根据研究现状与所做的实证分析，提出如下几点建议。

（1）对于相关监管部门与政府机构来说，要完善信息披露制度，提高信息的真实性，确保投资者能得到准确的信息，为模型提供更加理想化的条件。

（2）政府与监管部门要加大监管力度，降低个人投资者的比例，适当增加集体投资占比，使投资结构更加合理。

（3）增加市场灵活性，使市场更加适合现阶段发展状况。

（4）对于投资者来说，要树立良好的价值观念，进行合理投资，促进证券市场的稳定运行。

本文以互联网金融行业作为研究样本，因此针对互联网金融行业提出以下几点建议。

（1）鼓励创新，促进互联网金融稳步发展。积极推进互联网金融平台开展创新活动，以创新激发市场活力，引导金融机构学习宣传并广泛开发互联网技术，实现服务的跨越升级，使金融服务活动不局限于传统的金融体验，鼓励各机构广泛开展合作，利用自身资源推陈出新，以获得互补利益。

（2）明确互联网金融监管责任，强化消费者权益保护意识。在保护消费者的权益方面，各部门要研究出台一些政策措施，编写针对保护互联网金融消费者权益方面的文件，并及时传播，使消费者得到相关知识的教育，了解互联网金融融资问题，加强宣传。此外，要有一个专门解决金融消费争端的渠道，不论投资者本身资金是否充裕，都不需要因冗长的时间成本与较高的诉讼成本担忧，出现问题后双方可以通过私下协商化解矛盾冲突，跨越地域限制，降低成本，提高效率。除此之外，对互联网金融消费者进行合理教育也是一个保护其正当权益不受侵犯的有效方法，全方位地提高互联网用户的风险防范意识和自我保护能力。

（3）切实保障网络与信息安全，营造安全稳定的互联网金融环境。开发商与安全运营商应有效提高技术要求，安装高效的安全防火墙，妥善保护客户信息，对交易信息做好保密工作，不参与未经授权的交易或客户个人身份的披露；金融监管部门以及国家安全部门要做好对相关从业机构的网络安全进行监管，建立统一的安全保障标准，保障网络与信息安全有序。

参考文献

［1］BLACK F，JENSEN M，SCHOLES M.The Capital Asset Pricing Model：Some empirical tests［J］.Studies in the Theory of Capital Markets Praeger，New York，NY，1972：79-121.

［2］FAMA E F，MACBETH J D.Risk，return，and equilibrium：empirical tests［J］.The Journal of Political Economy，1973，81（3）：607-636.

［3］FAMA E F，FRENCH K R.The cross-section of expected stock returns［J］.The Journal of Finance，1992，47（2）：427-465.

［4］施東晖.上海股票市场风险性实证研究［J］.经济研究，1996（10）：44-48.

［5］杨朝军，邢靖.上海证券市场CAPM实证检验［J］.上海交通大学学报，1998（3）：61-66.

［6］陈小悦，孙爱军.CAPM在我国股市的有效性检验［J］.北京大学学报（哲学社会科学版），2000，37（4）：28-37.

［7］孙鹏飞，苏莉媛，沈晔.资本资产定价模型在中国股市的拟合程度分析［J］.商业时代，2006（5）：51-52.

［8］高永涛，牟新建.关于CAPM模型的实证研究——以我国上市银行个股为例［J］.商场现代化，2010（4）：7.

［9］张虎，邹媛媛.基于CAPM模型的上海股票市场适应性检验［J］.统计与决策，2016（14）：164-166.

［10］方涛.基于CAPM模型对中国高铁板块股票的实证研究［J］.北京印刷学院学报，2017，25（4）：93-94，83.