金属期货价格与股票价格动态关联效应研究

李子厚

摘 要：有色金属行业上市企业的收益和原材料价格及金属产成品价格密切相关，两者的价格变化会造成企业净收益的波动，而利用期货套期保值可以合理地规避原材料成本波动风险及产成品收益风险，帮助企业更好地实现利润最大化。本文使用DCC-GARCH 模型分析铝期货收益率和相关上市公司的股票价格指数收益率之间的条件相关性。结果表明，铝期货价格对于铝行业上、下游上市企业股票价格均具有单向冲击效应，并且历史收益波动率在短期和长期都具有显著的持久性影响。此外，本文描绘了两种资产收益波动率间的动态条件相关系数，从而为做出合理的套期保值策略或套利策略提供了参考。

关键词：有色金属期货价格；股票价格；波动率；动态关联效应

一、引言

有色金属期货市场是我国资本市场的重要组成部分，其对金属价格的发现功能和套期保值功能是相关产业乃至金融市场得以平稳发展的“稳定器”。从全国范围来看，有色金属行业的企业大都位于矿产开采、金属冶炼、原材料生产和有色金属材料加工等的一个或几个产业链环节上。有色金属期货的价格波动会对相关行业上市公司的经营利润和股票价格产生直接且明显的影响。

铝现货方面，我国铝产能及铝产量常年位居世界第一，产量、消费量和净出口量巨大。国家统计局数据显示，2020年，氧化铝、电解铝、铝材产量分别为7313万吨、3708万吨、5779万吨，分别同比增长0.3%、4.9%、8.6%，贸易总额达272亿元，同比增长3.4%。铝期货方面，2020年上海期货交易所铝期货合约成交5286.47万手（单边），同比2019年的交易量3275.76万手（单边）上升61.38%。长期来看，铝现货和铝期货的价格虽然波动幅度会有不同，但其变动趋势和方向具有一致性，随着期货合约到期日的臨近，两者价格逐渐聚合，基差接近于0。铝行业上市企业的利润及股票价格与金属铝价格波动联系密切，以及上市公司股票价格变动具有行业板块内的联动特性。可知铝原材料价格及产成品价格显著影响企业的预期利润进而影响股票价格。2021年第一季度末至第二季度，伴随美联储等各国央行宽松的货币政策及各国经济复苏，全球大宗商品价格普遍持续上涨，带动我国铝行业股票价格一度疯涨。因此探究有色金属期货市场价格和与之相关的上市公司股票之间关联性具有较强的理论意义及现实意义。首先可为相关行业的企业提供套期保值信息，从而帮助企业有效避免原材料的价格波动对其生产经营活动的影响。其次可为上市企业股票市值管理提供决策依据。再次可为股票投资者的交易提供参考。最后为金融主管部门提供合理的期货市场建设建议，促进资本市场的完善和发展。

二、文献综述

关于大宗商品价格和股票价格间的相关性分析自20世纪80年代末以来逐步成为学术热点之一。主要有以下两个方面。一方面，一国国内期货市场和股票市场间的关联效应研究。Geczy等的研究结果显示，上市公司参与期货交易的目的与该公司的经营现况有密切联系。Francis和Kim以小波分析法探究股票价格和股票价格指数期货价格的联动关系，结果表明两者收益率关系具有一定的持续性。Büyüksahin等分析了商品期货和股票指数关联性，得出两者之间存在正相关关系。石智超等基于产业链这一独特视角研究我国商品期货市场和股票市场间的联动关系，最终得出铝、锌和铜等有色金属期货价格的涨跌和上游及下游产业上市公司股票价格涨跌存在双向风险溢出关系。周伟和龙美芳选取2007年1月4日至2015年10月9日的铜行业股票价格、现货及期货数据，运用Granger因果检验、广义脉冲响应函数等方法研究了铜行业上市公司股票价格、期现货和铜货铜之间的交叉影响，研究结果显示，江西铜业和铜现货、铜期货、铜产业股票价格指数都无显著Granger因果关系。为进一步探讨股票市场和商品期货市场之间存在的双向溢出效应，Karanasos等的研究结果表明在金属期货收益率的波动溢出效应具有时间上的惯性。TIWARI等研究了原油期货、黄金期货与中国十大行业股票市场之间的非对称收益溢出，结果表明，商品期货收益率和十大行业的股票收益率之间存在时变的不对称溢出。邹绍辉和张甜的实证研究显示了能源股票市场、能源期货市场和碳市场三者间表现出结构变化及一定的非线性特质。另一方面，国际大宗商品期货市场和股票市场间的关联效应研究。金洪飞和金荦使用双因子GED-GARCH（1，1）-M模型，以2001年1月到2009年12月的国际油价数据和股票数据为样本研究了国际石油价格与中国14个行业的股票收益率之间的关系。结果显示，国际油价对天然气产业的股票收益率有正影响。Mensi Walid等利用2000年1月14日至2017年3月31日的周度数据研究了石油—股票的回报波动率相关性。为了更加稳健，该文章同时使用了WTI和布伦特原油石油价格，运用不同的滞后结构和不同的预测范围来检查整体溢出指数的敏感性，得出总溢出持续性在主要股票市场的回报和波动率系列中具有动态波动特性。王佳等的研究表明，TVTP-DCC-GARCH模型在套期保值有效性上比其他模型更优，在多元GARCH模型中引入时变状态转移概率可优化套期保值结果。

中国证券期货2022年9月

第3期金属期货价格与股票价格动态关联效应研究

从现有研究来看，有关商品期货市场和股票市场的关联性研究非常活跃，研究对象主要涵盖了两者之间有无显著相关性、国际大宗商品市场对一国股票市场的冲击、期货价格对股票价格的非对称冲击等方面。但值得注意的是，现有研究存在如下不足：第一，缺乏期货市场波动对具体产业的股票价格冲击的影响研究；第二，大部分研究验证两者价格之间相关性但没有计算出收益率的动态相关系数；第三，较少有学者将一个产业的上市公司分成上游企业组和下游企业组，并分别研究处于产业链不同环节上市公司的股票价格和期货价格的联动效应。为此，本文基于既有研究，以铝期货为例，对上述问题进行拓展分析。

三、样本选取与指标体系构建

（一）期货数据选取及指标构建

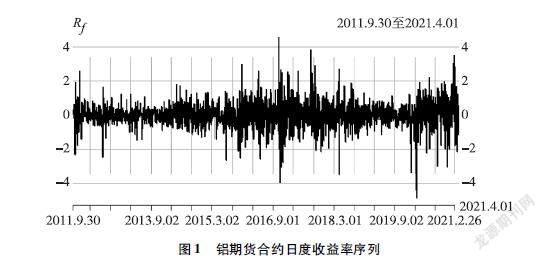
本文选取锐思数据库（RESSET）中2011年9月30日至2021年4月1日（共计2307个交易日）的铝主力期货合约的日结算价Pf_Al作为铝期货合约价格序列。参考郑振龙和杨伟的做法，定义Rf为铝期货合约的日度收益率序列（下同），其为铝期货对数收益率的100倍。

铝期货合约日度收益率序列Rf的时序图如图1所示：

（二）股票数据选取及指标构建

1.股票数据选取

截至完稿，我国铝行业上市公司共21家，本文依照鋁产业链中生产经营状况良好以及主营业务收入中铝产品占比较高的基本原则选取研究样本。从国泰安数据库里选取铝行业上游上市公司6家，分别是焦作万方、南山铝业、神火股份、新疆众和、云铝股份、中国铝业；下游上市公司6家，分别是常铝股份、宏创控股、闽发铝业、明泰铝业、宁波富邦、亚太科技。以上述12家上市公司的日度股票价格数据为基础样本，样本区间为2011年9月30日至2021年4月1日，该区间包括了2015年的牛市及股灾、2016年元旦后的熔断以及新冠肺炎疫情暴发期和后疫情时代，比较具有代表性。

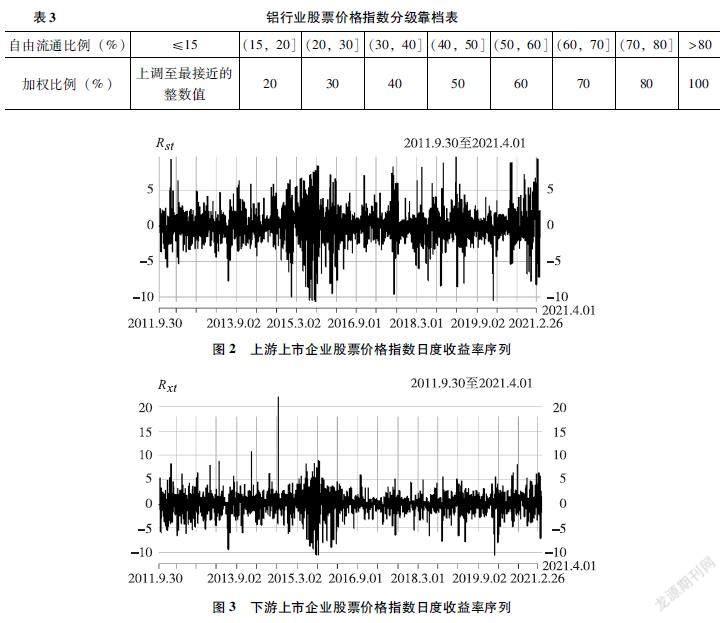
上、下游各6家上市公司的基本概况如表1和表2所示。

2.股票数据指标构建

为规避股票价格非同步波动和上市公司停牌的影响，本文将上、下游各6家上市公司股票价格序列严格按照《中证指数有限公司股票指数计算与维护细则》编制成股票价格指数，基期为2011年9月30日，基期值为100点。

指数计算公式：

报告期指数=报告期样本的调整市值基期市值×100（2）

其中，调整市值 = ∑（证券价格×调整股本数）。指数计算中的调整股本数系根据分级靠档的方法对样本股本进行调整而获得。要计算调整股本数，需要确定自由流通量和分级靠档两个因素。为反映市场中实际流通股份的变动情况，本文创建的股票价格指数剔除了上市公司股本中的限售股份，以及由于战略持股或其他原因导致的基本不流通股份，剩下的股本称为自由流通股本，即自由流通量。本文所构建的指数样本的加权比例按照表3确定。

定义Rs为上游上市企业股票价格指数的日度收益率序列，定义Rx为下游上市企业股票价格指数的日度收益率序列。

四、股票市场和有色金属期货市场关联效应研究

Engle提出ARCH模型用于刻画金融资产收益率时间序列数据的特征，如收益率“波动聚集”性、序列自相关性、“尖峰厚尾”性等。在ARCH模型的基础上，Bollerslev提出GARCH模型，除可减少待估模型参数外，该模型更具一般性。为研究多变量之间的收益和风险关系问题，GARCH被扩展到多元GARCH过程，即向量GARCH过程，其中一个典型代表就是CCC-GARCH模型（常数条件相关GARCH模型），由Bollerslev在1990年提出。Engle对CCC-GARCH模型的相关系数矩阵为非时变相关系数矩阵这一假设进行了改进，新的模型假设为多变量间的相关系数矩阵是时变相关系数矩阵，提出了DCC-GARCH模型（动态条件相关GARCH模型），可得动态相关系数时序图，用于刻画变量之间的动态联动效应。

（一）DCC-GARCH模型

本文采用DCC-GARCH模型来研究铝期货价格和相关上市公司股票价格之间的动态关联效应，该模型的原理方程和建模过程如下。

1.模型原理方程

其中，式（5）为均值方程，rt是均值为0的N×1维的收益率向量，Ωt-1为t-1时刻可获得信息集，Dt=diag（σ1t，σ2t，…，σNt）为对角矩阵，Rt为时变的动态条件相关系数矩阵。式（6）中ωi为不随时间变化的正标量，λi为平滑系数。式（7）中εt～N（0，Rt）。式（8）中Qt为标准化残差序列条件协方差矩阵，S为非条件相关系数矩阵，I为单位向量，°为Hadamard积，A和B为系数矩阵。

本文列明了DCC参数的估计方法，和静态模型相比动态相关模型的不同之处仅在于允许R随时间变化。

除了条件方差矩阵是标准化矩阵外，Rt的参数化要求同Ht。

极大似然估计过程如下：

根据式（11）中正态性的假设列出如下似然函数，即方程（12）。若无上述假设，该方程仍将具有拟极大似然函数的特性。方程（6）仅说明每项资产都服从单变量GARCH过程的假设。

其中，Qt为协方差矩阵；Q—为标准化残差求得的无条件协方差矩阵；Qt*为Qt中对角元素的算数平方根构造的对角矩阵。αm和βn分别是DCC-GARCH模型中前期残差平方项的系数和前期条件方差的系数；m和n分别为残差平方项的滞后阶数和条件方差的滞后阶数。约束条件：αm≥0，βn≥0且∑Mm=1αm+∑Nn=1βn<1。

2.计算过程

第一步先分别对Rst、Rxt和Rft三个收益率序列进行单变量的GARCH模型估计，得条件方差的估计值，进而得到标准化残差序列；第二步将第一步得到的标准化残差序列进行估计来获得DCC-GARCH模型动态条件相关系数图。

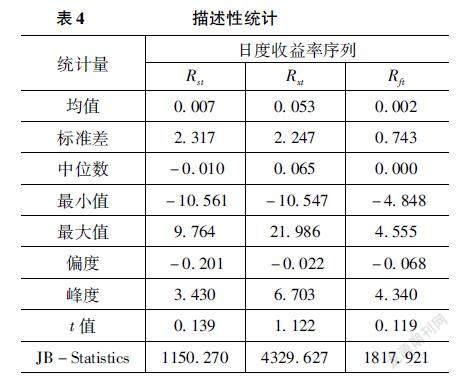
（二）描述性统计

表4列明了Rst、Rxt、Rft三个日度收益率序列的基本统计特征。根据表4中的偏度值均为负数来看，上述三个收益率序列呈现明显的左偏特性。三者的峰度值均大于标准正态分布的峰度值3，表明三个收益率序列都具有尖峰特性。此外，JB-Statistics亦表明三个收益率序列的分布呈现显著非正态性。

（三）单位根检验及ARCH效应检验

1.单位根检验

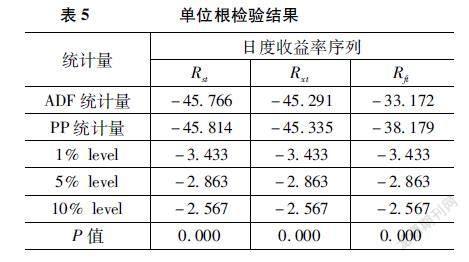
时间序列的平稳特征是建立时间序列模型的一个基本前提条件，在建立GARCH模型前，先对收益率序列进行平稳性检验。本节分别用ADF检验、PP检验来验证数据的平稳性，结果如表5所示。

ADF检验和PP检验的原假设为原时间序列为非平稳序列。从表5的统计结果可以看出三个时间序列的ADF统计量和PP统计量的绝对值远大于它们在1%显著性水平下临界值的绝对值，则拒绝原假设。Rst、Rxt和Rft三者均不存在单位根，都是平穩序列。

2.ARCH效应检验

本部分用ARCH LM-Test方法来分别检验Rst、Rxt和Rft这三个日度收益率序列是否存在ARCH效应（ARCH Effects），其原假设为不存在ARCH效应。

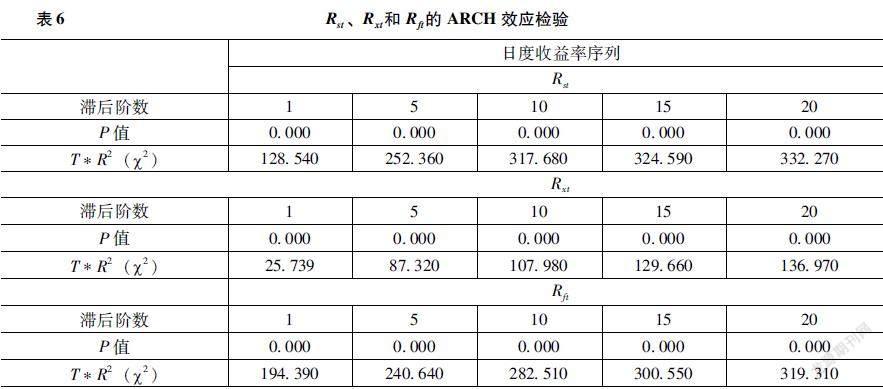
ARCH效应的检验结果如表6所示。

表6中的ARCH（LM）=T*R2，其中T为样本容量，R2为ARCH LM检验中辅助回归方程的拟优合度，T*R2服从渐进分布。

日度收益率时间序列Rst、Rxt和Rft的LM统计量的数值，即T*R2值均大于临界值，则拒绝原假设，得出3个收益率序列存在显著的ARCH效应。这为后续建立GARCH模型和DCC-GARCH模型提供了基础。

（四）GARCH模型及参数估计

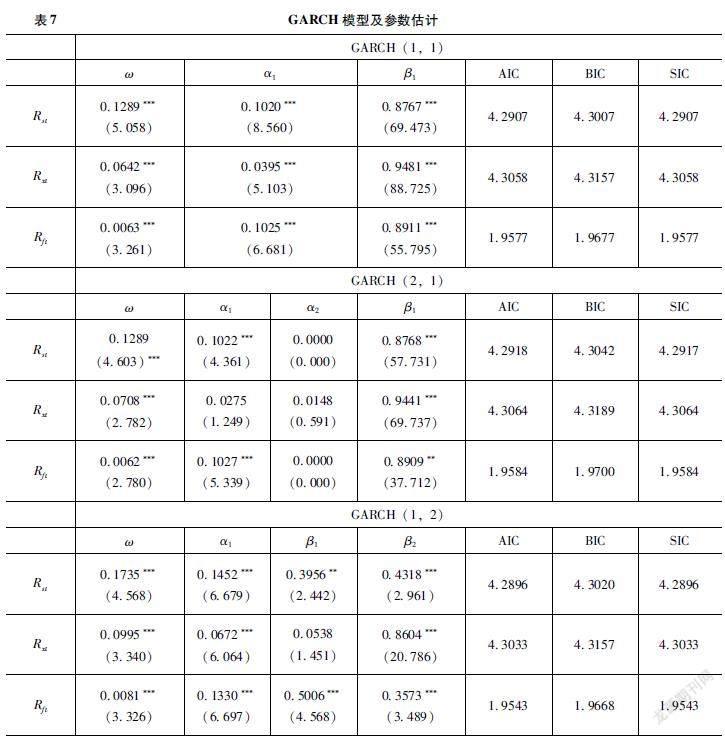
对Rst、Rxt和Rft分别建立GARCH（p，q）过程，为了确定模型的最优滞后阶数p*和q*，下面依次尝试建立GARCH（1，1），GARCH（2，1），和GARCH（1，2）模型，通过综合对比AIC准则、BIC准则和SIC准则来得出最优的滞后阶数，结果如表7所示。

由表7实证结果可知，以上3个波动率方程中的系数ω、α1和β1均在1%的显著性水平下显著异于0且均为正数。另外，α1+β1<1，模型是平稳的。

（五）DCC-GARCH模型参数估计

基于GARCH模型的实证结果，本节运用DCC-GARCH模型分别测度铝期货收益率和铝行业上游上市公司股票指数收益率以及铝行业下游上市公司股票指数收益率的动态关联效应。

首先采用极大似然估计法（Maximum Likelihood）估计方程（16）。

Qt=Q—（1-α-β）+αεt-1ε′t-1+βQt-1 （16）

方程（16）中，α为前期标准化无条件协方差矩阵的系数，表征滞后一期的标准化残差乘积对动态相关系数的影响，β为条件前期条件协方差矩阵系数，表征相关性的惯性，两者的数量关系满足α+β＜1。

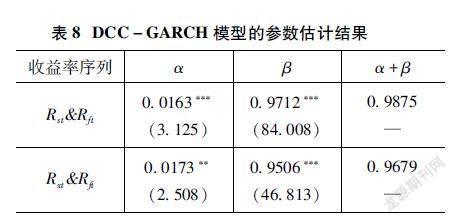
表8报告了基于多元的DCC-GARCH模型的铝行业上游上市公司股票价格指数收益率和铝期货收益率之间的DCC参数结果以及铝行业下游上市公司股票价格指数收益率和铝期货收益率之间的DCC参数结果。

表8DCC-GARCH模型的参数估计结果

收益率序列αβα+β

Rst&Rft0.0163***（3.125）0.9712***（84.008）0.9875—

Rxt&Rft0.0173**（2.508）0.9506***（46.813）0.9679—

由表8可知，α的估计值都比较小，但t值均超过了5%显著性水平下的t临界值1.96，表明动态相关系数受滞后一期的标准化残差乘积的影响较小。β的估计值都比较大，且均在1%的显著性水平下显著，说明前一期的收益率序列之间的相关系数对当期的相关系数有显著影响。此外，两者的α与β和均接近于1，说明Rst和Rft之间以及Rxt和Rft之间的相关性均具有较强的持续性。综上可知，铝行业上、下游企业股票价格和期货价格存在明显的关联效应。

（六）动态关联效应分析

1.动态相关系数R的描述性统计

两组动态相关系数R的描述性统计如表9所示。

由表9可知，R1的均值为0.2783，最小值为0.0422，说明铝行业上游股票价格指数收益率和铝期货收益率相关性较高，具有显著的正向效应，即随着铝期货价格的波动，铝行业上游企业股票价格随之发生同向波动。R2的均值为0.1783，最小值为-0.0103，但R2的2307个值中，仅有1个为负数，说明铝行业下游股票价格指数收益率和铝期货收益率相关性较高，亦具有显著的正向效应。

R1和R2对比来看，R1的均值大于R2的均值，说明铝行业上游上市公司股票价格与铝期货价格的动态关联性强于铝行业下游上市公司股票价格与铝期货价格的动态关联性。R1的标准差大于R2的标准差，可知上游公司股票价格和铝期货价格的动态时变的特征相对更加明显。

2.动态相关系数图分析

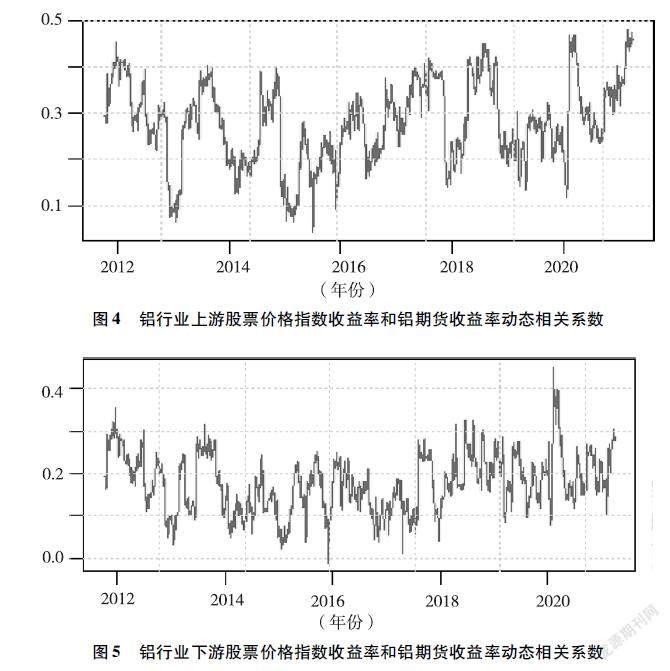
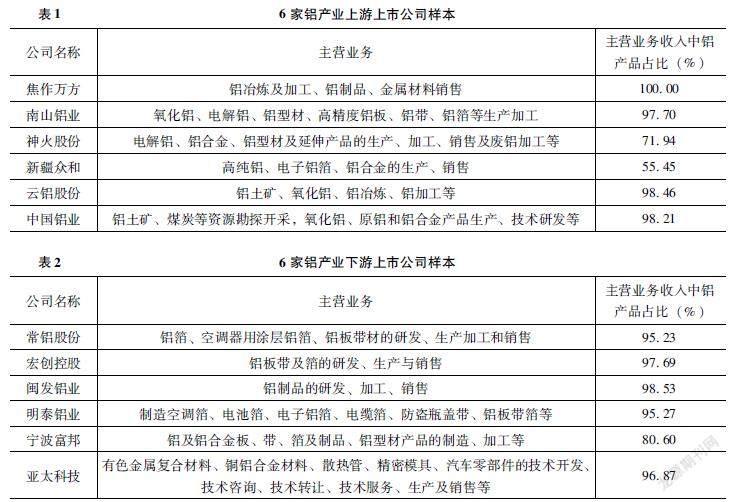
将DCC-GARCH模型估计出的动态相关系数制成动态相关系数图，图4和图5分别是铝行业上、下游股票价格指数收益率与铝期货收益率之间的动态相关系数图。

图4和图5反映了R1和R2总体变动趋势，可知上游企业的股票价格受期货价格的影响比下游企业显著。上游企业主要从事铝矿开采，铝冶炼，铝锭、铝板、铝带等产品制造，在一定产量下，这些产品的价格几乎决定了企业的销售收入，并且产品价格和铝期货价格走势在一定时期内基本一致。而下游企业以上游企业的产成品为原材料，主要生产电池箔、电子铝箔、电缆箔、有色金属复合材料、铝制汽车零部件等，随着期货价格升高，下游企业成本上升利润率降低，股票价格和上升的期货价格关联性降低。

另外，两个动态相关系数在特殊历史时期均处于比较低的水平，比如，2015年6月15日到9月25日的股灾时期和2016年1月4日至7月4日熔断时期，上、下游企业股票价格纷纷下挫，均已与期货价格关联度降低。

最后，进入2021年来，随着以美联储为代表的全球各大央行的量化宽松政策落地及后疫情时代的经济复苏，大宗商品价格持续走高，利好铝行业板块股票，使得铝行业上下游企业股票价格与铝期货价格关联性走强。

五、研究结论及相关建议

（一）研究结论

从长远看来，积极发挥期货市场的价格发现功能和套期保值功能是稳定经济发展的应有之义，如何使各行业的企业利用期货市场控制成本、稳定利润是金融界一直探索的问题。本文以金属铝作为有色金属的代表，用上、下游各6家上市公司近10年的股票价格按照《中证指数有限公司股票指数计算与维护细则》分别编制成股票价格指数，使用DCC-GARCH模型分别分析

图4 铝行业上游股票价格指数收益率和铝期货收益率动态相关系数

图5 铝行业下游股票价格指数收益率和铝期货收益率动态相关系数

上、下游股票价格指数收益率序列分别和铝期货收益率之间的相关性，以此来探究我国有色金属期货价格与关联行业股票价格的动态关联效应，进而提出相应的政策建议和投资建议。本文得出如下结论。

（1）从理论层面上看，大宗商品期货价格影响企业利润，进而影响企业股票价格波动，同时实证结果亦表明铝期货价格波动和铝行业股票价格波动存在显著且持久的单向波动溢出效应，同理论分析相符。

（2）2011年到2021年近10年的时期内，铝行业上游股票价格指数收益率和铝期货收益率动态相关系数R1的均值为0.2783，最小值为0.0422；铝行业下游股票价格指数收益率和铝期货收益率动态相关系数R2的均值为0.1783，最小值为-0.0103，说明铝行业上、下游企业股票价格和铝期货价格相关性较高，具有显著的正向效应，且呈现出明显的时变特征。

（3）铝期货价格波动对于铝行业上、下游企业股票价格的作用机制不同，影响程度不同，进而造成动态相关系数R1和R2的波动差异性，位于铝产业链不同位置的企业应采取不同的套期保值策略。

（二）相关建议

1.政策建议

期货市场对于稳定实体企业经营的重要性不言而喻，但目前大多数实体企业内部缺乏参与期货交易的专业部门和专业人才。建议期货交易所和期货业协会会同期货公司建立定期期货培训制度，辅导企业以相对较低的成本建立专业化的期货人才队伍。

此外，对于参与套期保值的企业可根据企业参与期货市场规模、企业的信用等级等指标，建立梯级保证金制度，参与规模越大并且信用评级越好的企业保证金比例越低。同时适度降低套期保值者的手续费，从而降低企业参与期货交易的门槛和成本。

2.投资建议

有色金属期货价格和与其相关联行业的上市公司之间股票价格具有显著的关联效应，对于投资有色金属板块股票的投资者来说，可将期货价格变动趋势作为买卖股票的重要参考信息之一，亦可开发股票市场和期货市场的套利策略。

投资者也可根据国内外相关联行业的企业经营情况来判断大宗商品期货市场的基本走势，进而建立跨市场、跨时期的多元套期保值或投机策略，以适应不断变化的市场行情。

参考文献

［1］ENGLE R F.Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation ［J］.Econometrica，1982，50（4）：987-1007.

［2］GECZY C，MINTON B A，SCHRAND C.Why firms use currency derivatives［J］.The Journal of Finance，1997，52（4）：1323-1354.

［3］ENGLE R F.Dynamic conditional correlation—A simple class of multivariate GARCH models［J］.Journal of Business and Economic Statistics，2002，17（5）：425-446.

［4］FRANCIS IN，SANGBAE KIM.The Hedge Ratio and the Empirical Relationship between stock and future Market：A new approach using Wavelet analysis ［J］.Journal of Business，2006，79（2）：799-820.

［5］BYKSAHIN  B，HARRIS J H.Do speculators drive crude oil futures prices［J］.The Energy Journal，2011，32（2）：167-202.

［6］KARANASOS M，ALI F M MARGARONIS Z，et al.Modelling time varying volatility spillovers and conditional correlations across commodity metal futures［J］.International Review of Financial Analysis，2018（57）：246-256.

［7］TIWARI A K，NASREEN S，ULLAH S，et al.Analysing spillover between returns and volatility series of oil across major stock markets［J］.International Journal of Finance & Economics，2020，26（2）：2458-2490.

［8］MENSI WALID，AL RABABAA ABDEL RAZZAQ，VO XUAN VINH，et al.Asymmetric spillover and network connectedness between crude oil，gold，and Chinese sector stock markets［J］.Energy Economics，2021，98（c）：105262.

［9］金洪飛，金荦.国际石油价格对中国股票市场的影响——基于行业数据的经验分析［J］.金融研究，2010（2）：173-187.

［10］郑振龙，杨伟.金融资产收益动态相关性：基于DCC多元变量GARCH模型的实证研究［J］.当代财经，2012（7）：41-49.

［11］石智超，许争，陈瑞.中国股票市场与商品期货市场传导关系的实证分析——基于风险Granger因果检验的研究［J］.金融理论与实践，2016（2）：82-89.

［12］周伟，龙美芳.我国期货铜和现货铜对证券市场铜行业上市公司股票价格变动的交叉影响分析［J］.金融理论与实践，2016（11）：92-98.

［13］王佳，金秀，王旭，等.基于时变Markov的DCC-GARCH模型最小风险套期保值研究［J］.中国管理科学，2020，28（10）：13-23.

［14］邹绍辉，张甜.能源期货市场、能源股票市场与碳市场非线性关系动态分析［J］.系统工程，2020，38（5）：1-13.