天绘二号双星InSAR成像与DSM生成技术
2023-01-14向建冰吕孝雷付希凯薛飞扬
向建冰,吕孝雷,付希凯,薛飞扬,云 烨,叶 宇,何 可
1. 中国科学院空天信息创新研究院,北京 100194; 2. 中国科学院大学电子电气与通信工程学院,北京 100049; 3. 中国科学院空天信息创新研究院空间信息处理与应用系统技术重点实验室,北京 100190; 4. 中国资源卫星应用中心,北京 100094
合成孔径雷达(synthetic aperture radar,SAR)是利用微波获取地面信息的主动式传感器,它不受天气条件限制,能够穿透雨雪雾,全天候、全天时获取数据,成为了高分辨率对地观测和全球资源管理不可或缺的手段之一,已广泛用于测绘、监测和水文学等领域[1]。星载合成孔径雷达干涉技术(InSAR)是对星载SAR图像进行干涉处理的一种技术,它可以生成数字地表模型图(DSM)、监测地形形变和实现三维重建,是全球大范围地形测绘最有效的观测技术之一。目前世界上能够用于InSAR处理的卫星主要有加拿大的RADARSAT系列,意大利的COSMO-SkyMed以及德国的TerraSAR-X/TanDEM-X系统[2]。文献[3—4]分别用ERS-1/2数据,TanDEM-X系统的数据利用InSAR技术实现了地形提取。而目前国产的SAR影像主要来源于高分三号,但高分三号重访周期长且轨道误差较大,时间去相干和大气去相干严重[5-6],大部分的高分数据不满足干涉测量条件,国内对于InSAR数据需求迫切。天绘二号是国内首个编队飞行的X波段合成孔径雷达卫星,相比于传统InSAR系统,编队飞行能够克服时间去相干和大气去相干等相干源,获得高精度的干涉对,对于提升我国遥感观测能力具有重大意义[7]。
卫星编队是指卫星在非常接近的轨道面上协同飞行,通过调整卫星飞行轨道的偏心率、近地点角和升交点赤经等,可以使双星具有3种灵活工作模式[8],分别为跟飞模式、双站模式和双站交替模式,其中双站模式是其中一颗卫星作为脉冲发射卫星,两颗卫星同时接收回波信号,即一发双收模式。与传统重轨干涉相比,双站模式具有0 s基线的独特优势,能够消去时间去相干源和大气去相干源[9],极大提高了有效干涉数据的质量和数量。
在双星SAR中,目标的距离历程与收发卫星均有关,其距离历程表现为双根式,使得无法准确解析驻定相位点,难用表达式表示回波信号的频域形式,而经典成像算法(如ω-k算法、CS算法、RD算法)的导出均基于回波信号的二维频域表达式。近年来,很多学者对于双站模式下的成像算法做了相关研究,文献[10]提出了适用于任何构型双基SAR的时域成像方法,这种方法可以产生最佳的图像质量但同时也带来了巨大的计算复杂性。与时域成像方法相比,频域成像算法能极大地提高处理效率,其中求解点目标的二维频谱是算法推导中重要的一步。文献[11—13]将平行构型的双基SAR斜距历程等效成单基SAR的形式,进而可以运用传统的单基SAR成像方法,例如Range-Doppler(RD)算法处理双基数据。文献[14]提出Loffeld 's bistatic formula (LBF)方法对收发相位历程在各自驻相点处二阶泰勒展开,得到任意构形下双基SAR点目标的二维近似频谱。文献[15—16]基于LBF方法并利用二维逆变标傅里叶变换(inverse scaled fast Fourier transform,ISFT)和chirp scaling (CS)算法聚焦双基数据。此外,文献[17]采用级数反演法(method of series reversion,MSR)来求解任意构形双基地SAR点目标的二维频谱。其中单站等效法可近似解析双星SAR二维频谱,同时后续处理可沿用传统单基成像算法,具有高效便利的优势,适合实际工程中双星SAR条带模式成像。
本文针对天绘二号干涉成像处理及三维重建进行了研究和试验,首先介绍了基于双曲等效的双星干涉成像扩展线性调频变标(extended chirp scaling,ECS)算法,并引入预滤波处理混合基线带来的图像间相干性降低和干涉相位误差等问题。然后阐述了干涉处理方法,设计了用InSAR技术重建DSM的技术流程。最后用天绘二号原始数据进行了干涉成像试验和干涉处理,并对成像结果和干涉处理结果进行了分析,验证了成像算法的聚焦性和保相性,以及干涉处理和三维重建的能力。
1 双星InSAR干涉成像
天绘二号SAR工作模式为条带模式,这种模式可以覆盖较大的幅宽,有利于完成大范围测绘任务[9]。双站模式下的天绘二号的轨道构型与TanDEM-X/TerraSAR-X系统类似[7],近似为一个螺旋式轨道,在一次成像时间内,两颗卫星可看作平移不变构型,即两颗卫星速度一致且基线保持不变。在双星成像算法中,双曲等效算法将单站等效算法扩展到了斜视情况并适用于平移不变构型[13],可以便利地求解平移不变构型下双基SAR点目标的二维近似频谱。因此笔者将双曲等效法和ECS成像算法结合来处理双星SAR数据。主辅星相对于目标的斜距历程可以表示为
(1)
式中,RT(t)和RR(t)分别表示主星和辅星相对目标的斜距历程;tc为场景中心时刻;t为方位向时间;Rm、Vm、φm分别表示双曲等效后的斜距、速度和斜视角;Rx,c、vx和φx,c(x=T,R)分别表示主辅星相对于目标点的斜距、速度和斜视角。
等效参数的计算如式(2)—式(4)所示的双曲等效方法完全等效了双星斜距历程的常数、线性和二次项,同时也补偿了部分三次及以上项[13]
Rm=(RT,c+RR,c)/2
(2)
(3)

(4)
将上述等效参数代入单站ECS成像算法中即可以实现辅星ECS聚焦成像,同时由于主星是自发自收,其成像方法可采用单星成像方法。
编队飞行的主辅星之间不可避免地存在沿航向基线和垂直航向基线,称之为混合基线。混合基线将引起主辅星回波数据间方位向多普勒谱偏移和距离波束谱偏移,导致主辅SAR图像间相干性降低和干涉相位误差等问题。
针对垂直航向基线引起的距离波束谱偏移导致的主辅图像间相干性降低和干涉相位误差问题,本文采用距离预滤波技术滤除不重叠的距离波束谱,即根据反射率谱移动量,截取公共的距离波数谱,再对具有公共距离波数谱的信号进行距离压缩处理。垂直航向基线导致距离波数谱偏移的解释如下:SAR天线接收的回波数据可以看作是地面反射率与入射信号的卷积,从频域上看是地面反射率谱与信号谱的乘积,其表达式如下
(5)
(6)
式中,R(ω)为地面反射率的傅里叶变换;ω0为雷达中心频率;θ1和θ2分别为两颗卫星的下视角;θ=(θ1+θ2)/2;β为地面坡度;W(ω)为SAR系统发射和接收的带通滤波器,其带宽为B。不同下视角之间的地面反射率谱的偏移量为
(7)
式中,Δθ为视角差;f0为雷达载频。不重叠谱段(非相干谱段)相当于重叠谱段(相干谱段)的噪声,从而降低了相干性。因此必须切除不重叠谱段同时保留重合谱段。
针对沿航向基线引起的多普勒谱偏移导致的主辅图像间相干性降低和干涉相位误差问题,本文采用方位预滤波技术滤除不重叠的方位多普勒谱。具体实现方法如下:根据主辅卫星回波数据的多普勒谱中心频率和多普勒带宽确定出重叠的多普勒谱,并滤除非重叠部分的多普勒谱。
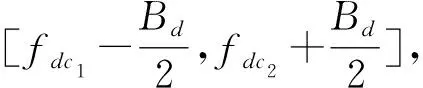
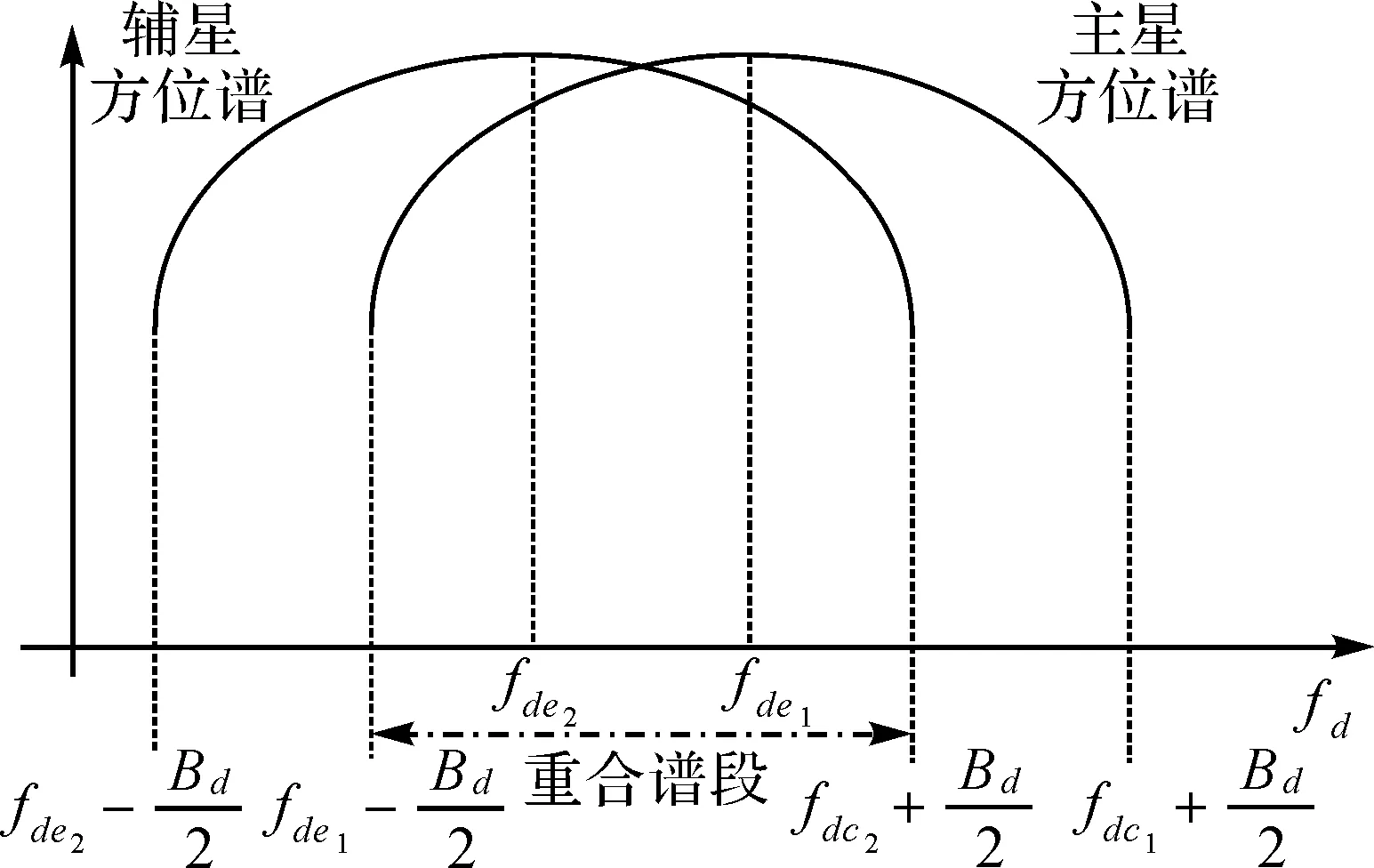
图1 方位预滤波多普勒谱段Fig.1 Diagram of azimuth pre-filtering Doppler spectrum
2 DSM生成方法
InSAR利用干涉相位信息,对同一区域的两幅SAR单视复图像进行干涉处理,生成DSM数据。InSAR处理要求两幅SAR图像具有较好的相干性,数字地表模型图(DSM)为干涉处理结果之一[18-19],它反映了图像区域的高度信息。双星模式下InSAR测量几何如图3所示,两卫星同时照射同一区域,去除了时间去相干性和大气去相干等去相干源,产生的图像对能直接用于干涉处理。

图2 干涉成像算法流程Fig.2 The flowchart interferometry imaging algorithm
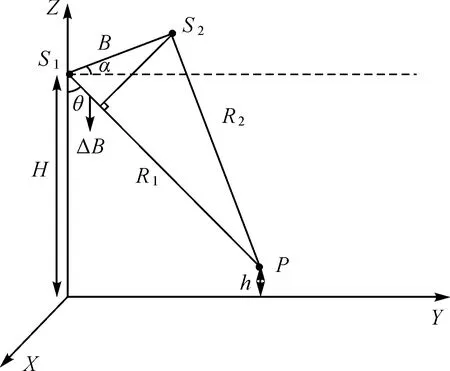
图3 InSAR测量几何Fig.3 The geometry of InSAR
图3中P点为A星、B星照射的同一目标点,P点的高程为h,S1、S2分别表示A星和B星在照射P点时的位置,R1、R2分别表示A星和B星到P点的斜距,B表示A星和B星之间的基线矢量,ΔB表示平行基线,α表示B与水平方向的夹角,θ为A星照射点的下视角,根据图2所示的几何关系可以把P点的高程表示为
h=H-R1·
(8)
由于干涉测量需要同一地区的两幅相干性很高的SAR图像,同时干涉相位不能直接从复图像中得到,实现DSM生成需要通过复图像配准、干涉图生成、干涉相位滤波、相位解缠、基线估计及DSM重建等步骤。因此本文设计了如图4所示的干涉处理流程来完成DSM生成。
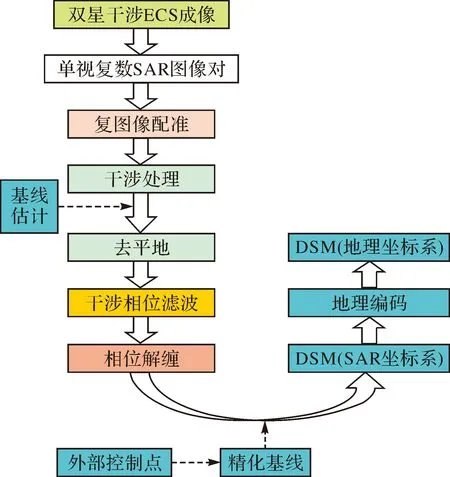
图4 DSM生成流程Fig.4 The flowchart of DSM generation
复数图像配准是干涉处理第1步,包括两幅单视复图像之间的偏移值多项式计算和复影像重采样[20-22],两幅影像配准精度要优于0.1像元,然后对配准好的复图像进行干涉处理,得到干涉条纹图。配准后干涉所形成的相位条纹密度一般较大,不利于后续相位滤波和解缠处理,通过基线估计计算条纹频率来去除平地相位得到去平地后的干涉条纹图。为了抑制干涉相位图中的噪声,提高相位解缠的效率和精度,本文采用自适应滤波对相位进行降噪处理[23-24]。在得到解缠相位图后,通过外部控制点精化基线重建DSM,其中基线是干涉处理中的一个重要参数,基线的长度和指向直接影响着图像的相干性、测高灵敏度等,它也是影响DSM重建的精度的最重要误差源之一[25-27],在干涉处理中先通过轨道法和快速傅里叶变换法估计基线来去除平地相位[28-30],后续通过引入外部控制点精化基线。
其中基于轨道法的基线估计是从基线的空间几何关系出发,利用已知的卫星轨道状态矢量来获得基线分量的一类方法,得到的基线只能是真实基线的一个近似解。基于快速傅里叶变换法的基线估计主要利用干涉图中蕴含的信息如干涉条纹、干涉相位差等来估算基线分量。在轨道信息不完整或者精度较差的情况下,采用基于快速傅里叶变换的基线估计方式可以很好克服这个影响。相位与基线的关系满足
(9)
代入卫星高度H=R1cosθ得
(10)
则有
(11)
令
则有
(12)
式中,rmin和rmax对应边缘像元的斜距;kmin和kmax分别是干涉条纹相对应的函数谱,可从如下解缠相位的傅里叶变换中得
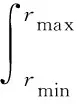
基线精估计是基于解缠相位、对应地面高度、基线之间的关系建立起来的方程,通过解这个方程可以求解出基线信息。对于地面点Ti的干涉相位观测值为
式中,φi为Ti的解缠相位;φc为常数相位;rmi和rsi分别为地面点Ti至主影像和辅影像的斜距。斜距关系为
式中,Bx、By、rmix和rmiy分别为基线距rmi的x、y分量,则有
(13)
式中,θi为地面点Ti的视角;H为雷达高度;hi为地面点高度;rg为地球半径。由于参数Bx、By、H和φc的变化率很小且呈线性。当已知至少7个地面控制点时,可以解出未知参数Bx0、Bx1、By0、By1、H0、H1和φc。地面外部控制点的精度对最终的结果有一定的影响,并且控制点的数量也会有一定的影响,通过合适地选择控制点,能够精确地算出基线信息,而且该基线结果还能消除由于初始基线不准确引起的DSM相对偏移和倾斜。
在生成DSM时,由于双星编队下辅星成像几何与主星自发自收的情况不同,需要结合干涉相位方程、斜距方程和多普勒方程求解三维定位,此处可采用双基等效相位中心法或联合主图像信息的等效相位中心法[31]。
3 试验结果与分析
3.1 成像试验
本文所选试验区为某试验场山地区域,A星和B星工作模式为双站模式,其中B星为主星,A星为辅星,两星均用同一波位观测。对原始回波解压缩后用基于双曲等效的双星干涉ECS成像算法处理,图5为该地区的成像结果。

图5 跟飞模式下双星成像幅度Fig.5 Amplitude figure of two satellites imaging in follow-flight mode
在A星成像幅度图的红色矩形框圈出的区域中找到一个角反射器,如图6(a)所示,对它插值128倍,结果如图6(b)所示,可见辅星聚焦质量很好。
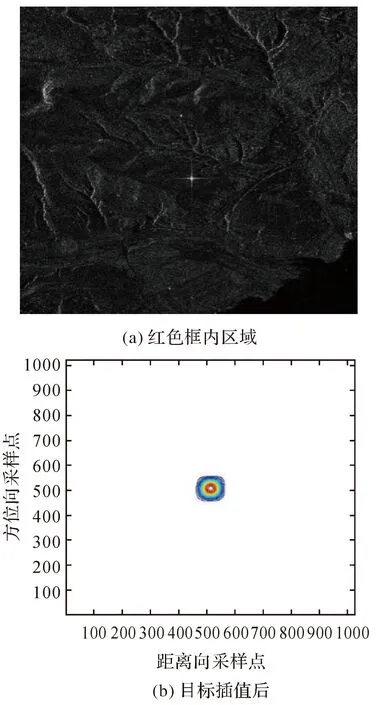
图6 角反射器成像结果Fig.6 Imaging result of corner reflector
3.2 干涉处理与DSM生成
选取3.1节中的双星模式下的复数SAR图像对进行干涉处理,干涉处理技术流程如图4所示。首先需要对复数SAR图像对进行裁剪和配准,配准后距离向配准精度为0.051像元,方位向为0.02像元,满足干涉处理要求。相干性是影响地形提取的重要因素,图7是截取区域配准后的相干性图,图中红色区域为相干系很好的区域,绿色和蓝色区域表示相干性较差区域,可以看出SAR图像对整体相干性非常好,双星模式下的双星SAR图像具有很好的相干性。
图8显示了干涉处理结果,其中图8(a)是干涉条纹图,对其进行去平地处理,得到如图8(b)所示的地形高程变化引起的相位变化。数据所对应的基线为556.628 1 m。然后,用最小费用流法(MCF)对滤波后的去平地后相位进行相缠,得到如图8(c)所示的解缠相位图。在求解三维定位后,采用精化后的基线生成数字高程图,并转换到地图投影坐标系下得到图9中地理编码后的RAWDSM。

图7 相干性示意Fig.7 Coherence illustration
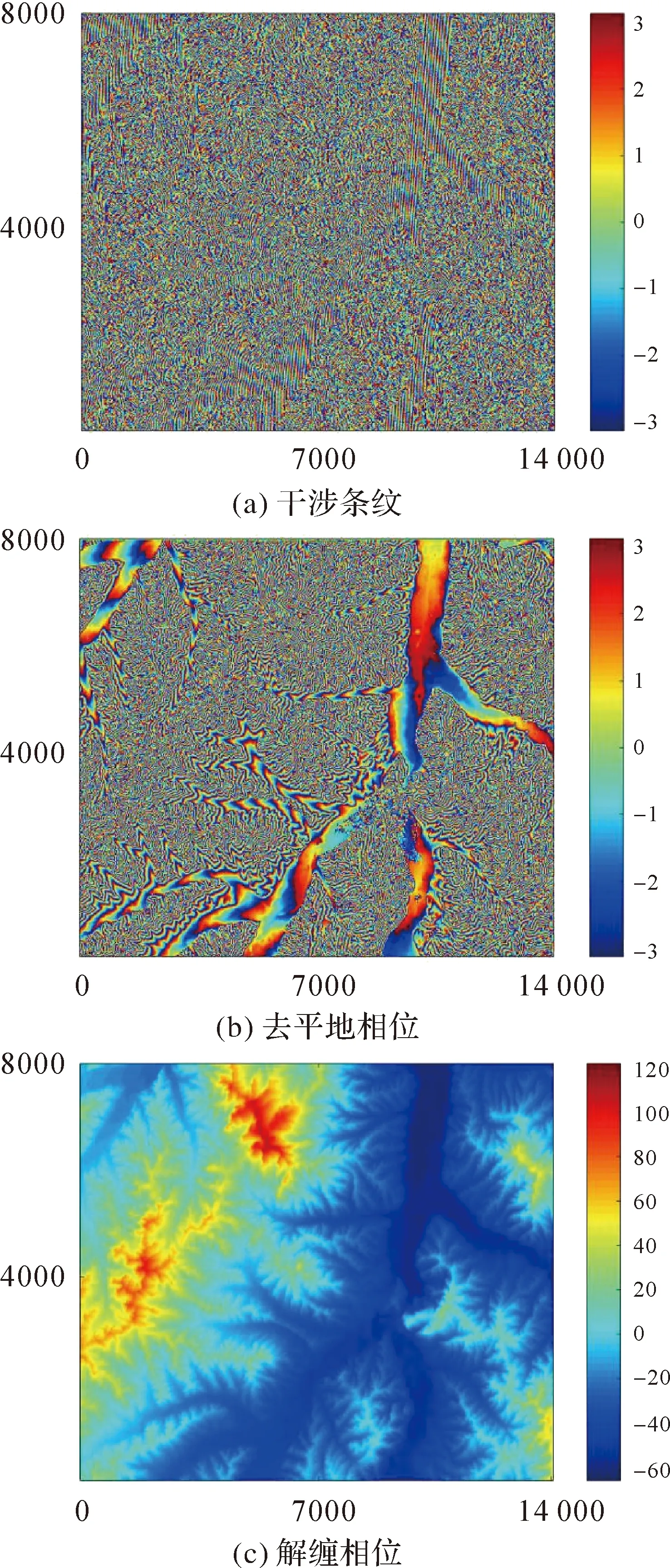
图8 干涉条纹与解缠相位Fig.8 Interference fringes and unwrapped phase
图9(a)为利用试验场山地区域SAR图像数据进行干涉处理和DSM重建后得到的该地区的数字高程图,图9(b)为同一地区的SRTM DSM,可以看到,本文处理生成的DEM与SRTM的DSM相比,整体地形轮廓与变化趋势及细节几乎一致,验证了成像算法的保相性和数据的干涉测量以及三维重建能力。

图9 数字地表模型图(DSM)Fig.9 Digital surface model (DSM)
4 总 结
本文对双星模式下的InSAR干涉成像和三维重建进行了研究和试验。首先介绍了基于双曲等效的双星干涉ECS成像算法,然后阐述了DSM重建原理与技术流程。本文选取了天绘二号双星模式下的某试验场附近区域数据进行了成像试验和DSM重建试验,成像试验结果验证了干涉成像算法的良好聚焦性,配准后的数据的相干性图反映了双星模式下的天绘二号数据的高相干性,最后干涉处理与DSM重建结果验证了干涉成像算法的保相性和天绘二号的良好InSAR能力。
