天绘二号卫星双基成像几何模型改正算法
2023-01-14钱方明刘志铭楼良盛
陈 刚,钱方明,刘志铭,楼良盛
1. 地理信息工程国家重点实验室,陕西 西安 710054; 2. 西安测绘研究所,陕西 西安 710054
天绘二号卫星于2019年4月发射,通过双星绕飞编队、一发多收的工作模式获取高相干性回波数据[1],可应用于地形测绘、形变和灾害监测[2-4]。由于辅星与主星沿飞行方向最大存在约800 m的距离,为了确保成像精度,辅星在成像时采用了收发分置的双基成像几何模型(bistatic imaging geometric model)[5]。为了成像算法统一,主星成像时也采用了双基成像几何模型。主辅星成像几何模型直接影响着InSAR数据处理的多个环节,包括影像概略配准、去平地效应、InSAR定位、基线定标、区域网平差、正射纠正等。对于影像概略配准、去平地效应、InSAR定位等环节,采用双基成像模型只是增加了算法的复杂度,而对于基线定标环节,这带来了新的挑战:①现有基线定标算法均针对单基几何模型[6-18],无法直接应用到天绘二号中;②天绘二号主辅星收发分置成像,两两组合会形成4条基线,在进行基线定标时,4条基线存在相关性,导致定标精度降低,无法满足实际应用需求。
为了保证基线定标精度,必须对主辅星成像几何模型进行简化,使其转化为单基模型。对于辅星而言,通常构建等效相位中心模型,将辅星双基模型转换为自发自收模式[19-20]。文献[21]提出了联合主辅图像信息的辅图像等效相位中心法,该方法具有无须假设地面高程、精度高等优点,但等效后改变了辅星位置,无法用于后续基线定标。文献[22]提出了基于几何构形的等效相位中心方法,不用改变辅星位置,但对定标模型改正精度分析不够充分,并且也缺乏实际数据验证。
针对天绘二号主辅星成像模型改正需求和现有改正方法存在的问题,本文提出了主辅星双基成像几何模型的改正方法。对于主星,提出了将场景起始时刻向前移动一个斜距传播时间的方法,使主星变为单基模型。对于辅星,提出了对每个点进行干涉相位补偿的方法将其变为单基模型,并对补偿精度进行了分析:①在有地面控制点时,直接利用主辅星位置和控制点之间的距离差来计算待补偿干涉相位。②在无地面控制点时,利用辅星接收时刻斜距、速度、主星位置之间的几何关系,直接计算待补偿的干涉相位。利用天绘二号两景试验数据进行改正精度验证,试验结果表明,主星修正前后模型完全等效,辅星修正后InSAR定位精度会略有下降,损失在厘米量级,能够满足后续定标需求。
1 天绘二号卫星成像几何模型
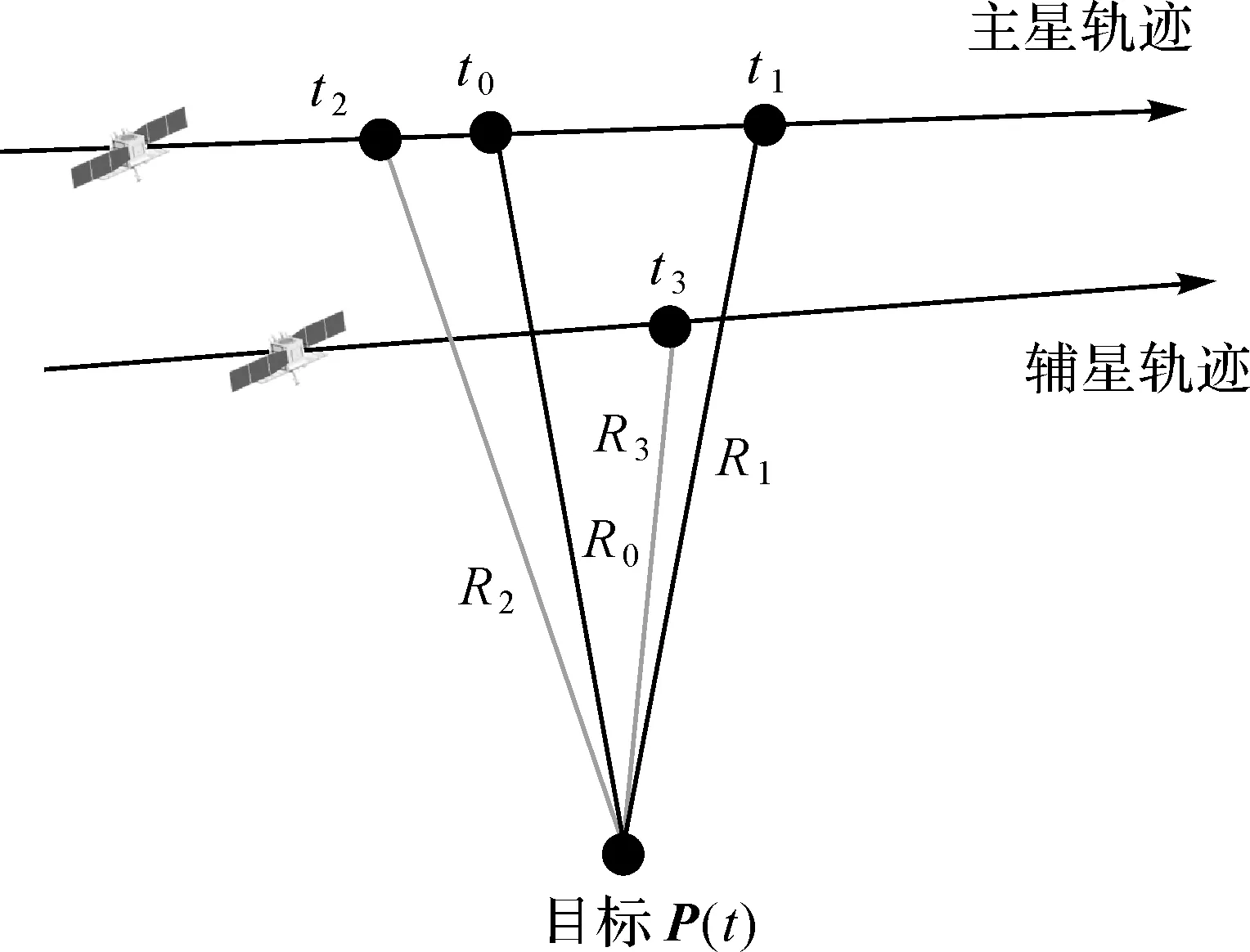
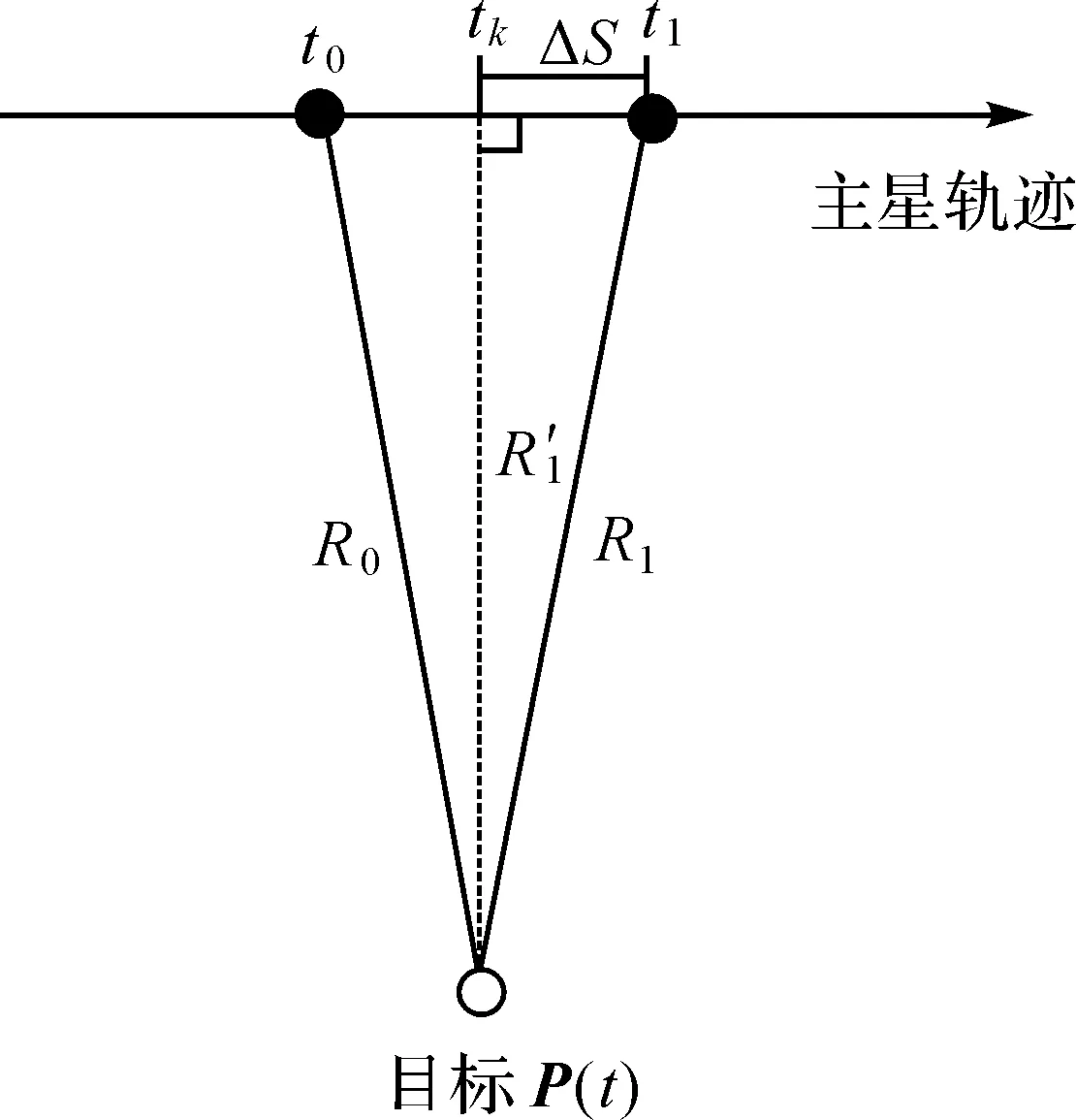
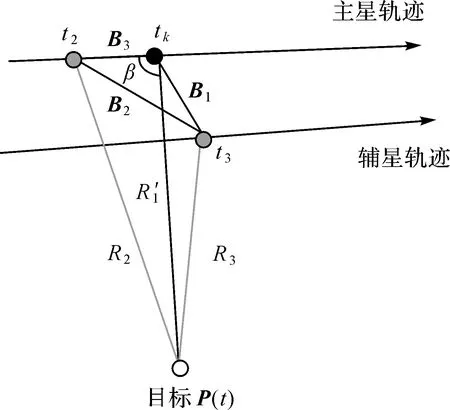
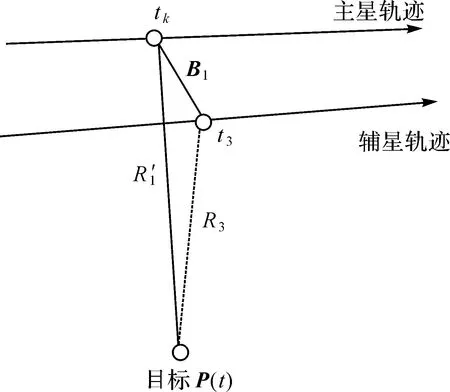
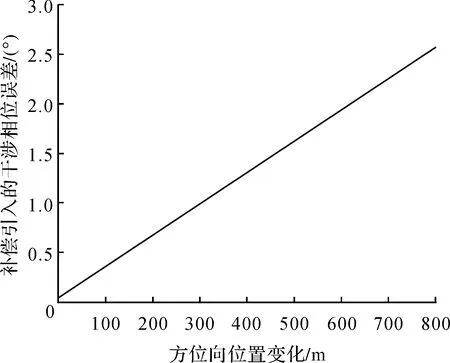
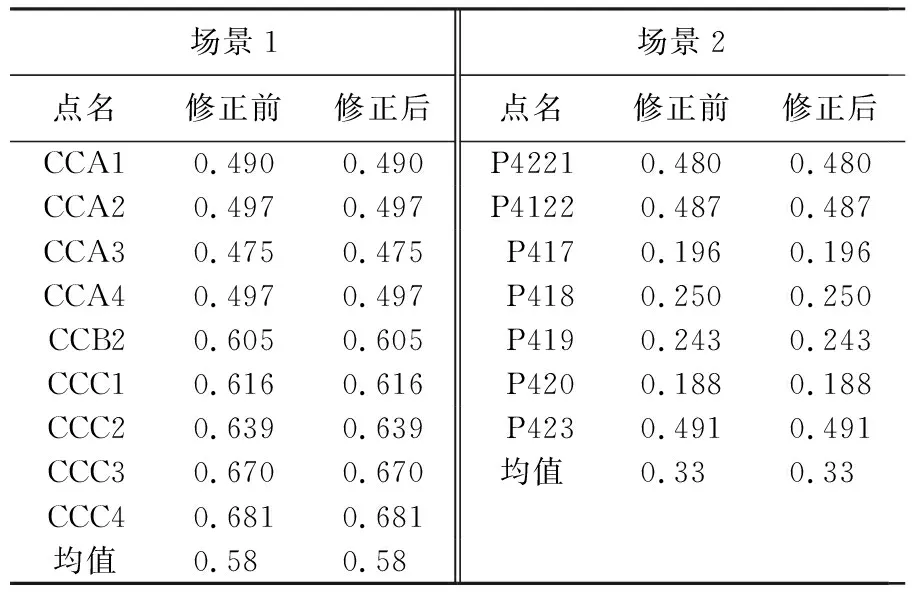
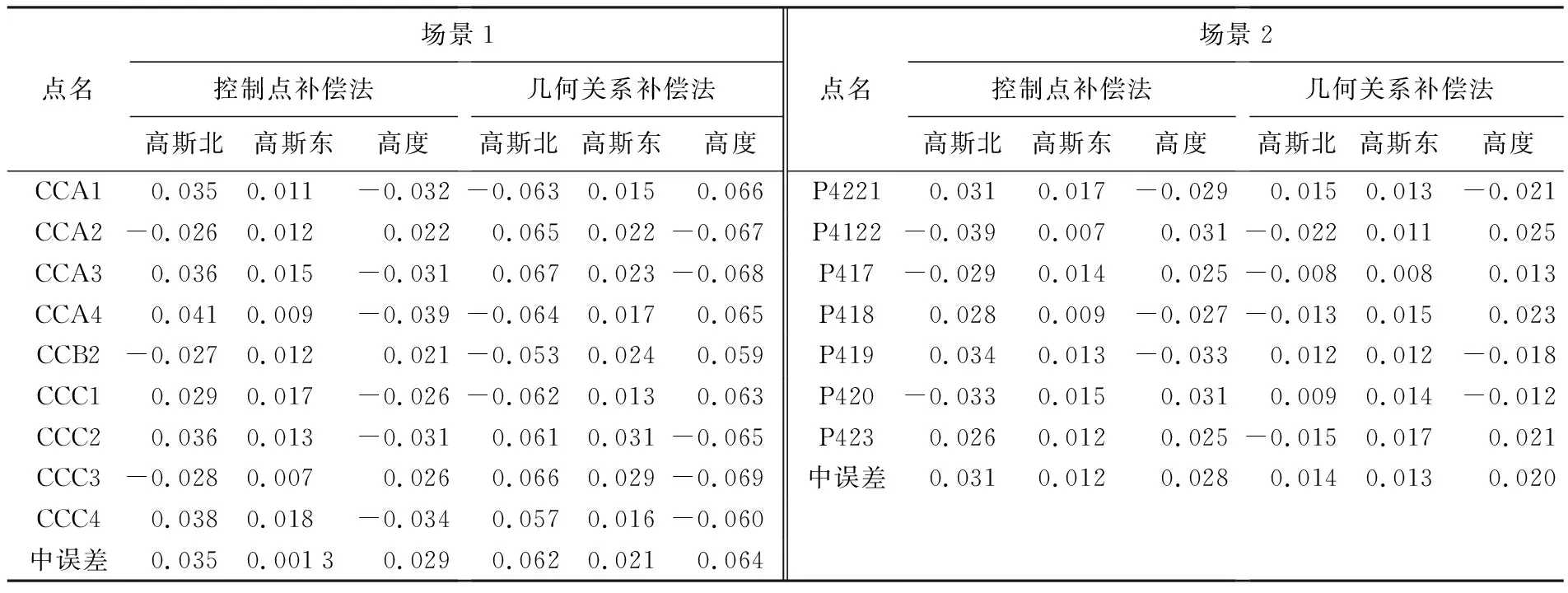
如图1所示,不失一般性,设主星在后,辅星在前。对于主星,在t1时刻接收主星t0时刻发射的信号,对于辅星,在t3时刻接收主星t2时刻发射信号,且t3 |P(t)-Pm(t0)|+|P(t)-Pm(t1)|=R0+R1 (1) (2) |P(t)-Pm(t2)|+|P(t)-Ps(t3)|=R2+R3 (3) (4) 图1 卫星成像几何Fig.1 Satellite imaging geometry 根据干涉测量原理,式(3)可以进一步表示为[24] |P(t)-Pm(t2)|+|P(t)-Ps(t3)|= (5) 式中,φ是绝对相位。联立方程式(1)、式(2)、式(5),通过迭代即可完成P(t)的求解。 主星成像几何模型修正的目的是将收、发统一至一个时刻(设为tk),并使修正后的fdm=0,此时P(t)与Pm(tk)连线垂直于主星轨迹,如图2所示。当P(t)坐标已知时,可以根据式(6)多普勒方程,准确找到tk (6) 图2 主星成像时刻Fig.2 Master satellite imaging time (7) 主星成像几何模型经过修正后,式(5)需要相应变化,变为 |P(t)-Pm(t2)|+|P(t)-Ps(t3)|= (8) 在将主星修正为单基模型后,主辅星成像几何模型如图3所示,此时仍会存在B1和B2两条基线。对于定标而言,两条基线之间依然相关,无法标定。考虑到B2是由于辅星收发位置不一致产生,因此必须将其消除。 对式(8)进行变换,考虑到|P(t)-Pm(t2)|=R2,则有 (9) 图3 主星等效后成像几何模型Fig.3 Equivalent imaging geometric model of master satellite (10) 对比式(10)与常规InSAR距离差方程[24,25],可以看出,只需要对当前点补偿一个干涉相位φcmp,那么辅星就可以变成单基成像几何模型,如图4所示。 图4 修正后辅星成像几何模型Fig.4 Fixed imaging geometric model of slave satellite 2.2.1 控制点补偿法 (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) 图5 补偿引入的干涉相位误差Fig.5 Compensation for the interferometric phase error introduced 由图5可以看出,利用控制点进行修正引入的干涉相位误差与方位向基线长度基本成正比,方位向基线越长,补偿引入的误差越大。最大误差为2.7°左右,按照高程模糊度30 m计算,引起的高程误差为0.22 m,基本可以忽略不计。 2.2.2 几何关系补偿法 设B3=Pm(t2)-Pm(tk),根据三角定律,可得 (21) 当t2与tk时刻较近时,可以认为Pm(tk)与Pm(t2)的连线与速度V(tk)的方向相同,而根据式(7)可知 (22) 此时,式(11)可变为 (23) 需要指出的是,利用多普勒方程来求解β的前提是t2与tk时刻较近。当t2与tk时刻较远时,利用多普勒方程计算出的夹角和实际夹角有一个差异。经过对在轨实际数据的统计,两个角度差异最大可达0.002°。 影响φcmp的主要误差源有斜距误差mR、基线B3模值测量误差m|B|、速度模值误差m|Vm|,各误差对φcmp的误差传递系数如下 (24) (25) (26) 轨道高度为514 km、速度为7.4 km/s、斜距为640 km、速度精度为0.002 m/s(三轴)、斜距误差mR为1 m,B3基线模值变化范围为[-800 m,800 m]。与2.2.1节一样,m|B|误差与方位向基线变化相关,补偿引入的干涉相位误差mφ与方位向基线B3之间的关系如图6所示。可以看出,该方法引起的误差较控制点补偿法小,但这是没有考虑β角近似的情况。以β角近似引起0.000 01°误差为例,在B3变化范围为[-800 m,800 m]时,引起的干涉相位最大误差为1.6°。因此如果考虑β角近似引起的误差,那么该方法引起的误差大于控制点补偿法。 图6 补偿引入的干涉相位误差Fig.6 Compensation for the interferometric phase error introduced 为了验证本文方法的有效性,利用两景天绘二号卫星数据进行试验。场景1地点为河北赤诚,获取时间为2019年9月26日,入射角为41.19°、斜距为701.33 km、影像采样间隔为2.027×0.936 m(方位向×距离向)、高程模糊度为27.09 m,共布设了9个控制点,一景内主辅星沿方位向距离变化范围在110~130 m之间,原始影像、概略覆盖范围分别如图7(a)、(b)所示。场景2地点为新疆哈密,获取时间为2019年9月26日,入射角为34.16°、斜距为626.15 km、影像采样间隔为1.53×0.936 8 m(方位向×距离向),高程模糊度为20.54 m,共布设了7个控制点,一景内主辅星沿方位向距离变化范围在86~91 m之间,原始影像和概略覆盖范围分别如图7(c)、(d)所示。 图7 试验数据Fig.7 Experimental data 评价主星成像几何模型修正精度方法是比较修正前后多普勒方程的残差,修正前后分别利用式(2)、式(7)计算,表1给出了比较结果和最终统计均值。 表1 主星成像几何模型修正精度对比 由表1可以看出,无论是场景1还是场景2,修正后多普勒方程残差与修正前完全相同,在0值附近,说明本文提出主星成像几何模型修正后与原方程等效,没有引入新误差。 评价辅星成像几何模型修正精度方法是比较修正前与修正后控制点InSAR测量坐标之差,即联立式(1)—式(3)求解每个控制点修正前坐标,再联立式(1)、式(2)、式(10)求解修正后坐标,然后计算修正前后坐标之差。由于比较的是修正前后控制点InSAR测量坐标之差,而不是比较InSAR测量坐标与控制点外业测量坐标之差,因此在修正模型精度高的情况下,其差值很小(表2)。 表2 辅星成像几何模型修正前后定位精度 采用控制点法进行补偿,根据主辅星一景内沿方位向距离的变化,计算出理论上引起的干涉相位误差最大分别为0.5°、0.4°,再根据各自景的高程模糊度,计算出理论上对应高程误差为0.037、0.023 m,而实际处理结果分别为0.029、0.028 m,与2.2节理论分析吻合,说明了方法的有效性。采用几何关系法进行补偿,如果只看图6,引起的干涉相位误差量级在0.001°,等效前后应该相等。但在2.2.2节也指出,该方法利用多普勒方程计算出的夹角β和实际夹角有一个差异,对两个场景所有控制点β角进行统计,场景1和场景2的夹角差异的均值分别为0.000 035°、0.000 011°,由于β角近似引入的干涉相位误差分别为0.9°和0.31°,对应高程误差分别为0.066、0.21 m,控制点实际处理结果分别为0.064和0.020 m,也说明了本文方法的有效性。 由表2还可以看出,无论哪种方法,其补偿引起的误差与地形关系不大。采用控制点补偿法,补偿结果较为稳定,其精度主要取决于轨道、控制点和速度精度,而几何关系补偿法主要取决于夹角β近似引起的误差。需要指出的是,辅星是通过逐点补偿干涉相位来进行模型修正,由式(11)、式(21)可知,补偿的干涉相位与主星位置、基线三轴分量、主星斜距等因素相关,每个点的补偿结果不一样,当前场景的补偿结果无法应用到下一场景。对于基线定标,场景中会布设高精度控制点,此时两种补偿方法都可使用,但控制点法精度更高;对于其他应用如区域网平差,场景中只有少量控制点甚至没有控制点,此时可以采用几何关系法对每景数据进行补偿。 天绘二号卫星主辅星均采用双基成像几何模型,对于后续基线定标带来困难。为了简化定位模型,保证基线定标的精度,本文提出了主辅星成像几何模型修正方法,并从理论上分析了修正精度。修正后,主辅星成像几何模型均变为单基成像几何模型。利用天绘二号两景数据对修正精度进行了试验,试验结果表明,主星修正后与修正前完全等价,辅星修正后系统定位精度有所下降,下降在厘米量级,基本可忽略不计。利用修正后的成像几何模型进行基线定标,定标后绝对平面和高程精度分别提升了34%和44%。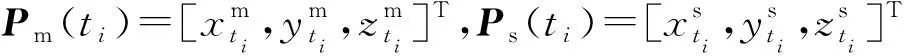
2 成像几何模型修正
2.1 主星成像几何模型修正

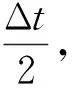
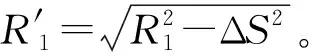
2.2 辅星成像几何模型修正

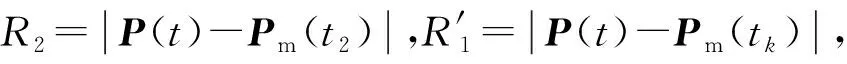

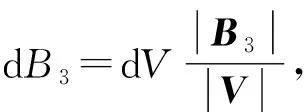


3 试 验
3.1 试验数据介绍

3.2 主星成像几何模型修正精度
3.3 辅星成像几何模型修正精度
4 结 语
