改进麻雀搜索算法优化支持向量机的井漏预测

王鑫， 张奇志*

(1.西安石油大学电子工程学院， 西安 710065； 2.陕西省油气井重点测控实验室， 西安 710065)

在钻井作业过程中，受到复杂地层、司钻操作失误等因素的影响，在钻井作业的任何阶段都有可能发生井漏。井漏事故不仅污染环境，还极有可能造成设备故障、威胁钻井人员安全等。如果在出现井漏后没有及时发现并采取堵漏措施，任凭其发展下去，严重的会发生井喷现象，可能会引起诸多连锁反应，从而导致井眼报废[1-2]。因此，在钻井过程中，能够及时预测井漏事故，显得尤为重要。

早期，针对井漏事故的预测，只能靠相关技术人员通过传感器采集到的实时数据进行人为判断。但这需要技术人员有着丰富的经验。而且，人为判断有着较大的主观因素。近年来，随着智能算法的不断发展，中外学者提出了许多井漏事故预测智能方法。这些方法更加科学，能够更准确地预测井漏事故。

耿志强等[3]使用移动窗稀疏主元分析法对钻井事故数据进行分析并建立了井漏案例库，将案例库中的钻井数据与实时钻井数据中的异常部分进行对比，从而判断可能发生的故障类型；刘彪等[4]使用破裂压力、孔隙度、原生裂缝方向等钻井参数分别建立了基于高斯核函数和多项式核函数的支持向量回归的漏失量预测模型。结果表明，采用高斯核函数的预测模型误差更小，可以更好地对井漏的漏失量进行预测；Abbas等[5]分别使用人工神经网络和支持向量机建立了井漏事故预测模型。最终，通过现场数据的验证表明，支持向量机在井漏预测方面比传统人工神经网络表现更优，预测准确率更高。Agin等[6]建立了自适应神经模糊推理系统预测井漏的模型，并使用数据挖掘技术，对钻井数据进行分析，确定了对井漏事故发生有较大影响的特征参数，进一步提高了井漏预测的准确率；Aljubran等[7]建立了基于深度学习和时间序列分析的井漏事故预测模型。结果表明，使用一维卷积神经网络能够有效地对井漏事故进行预测。

麻雀搜索算法受自然界中麻雀觅食过程的启发。已经有大量实验证明，麻雀搜索算法在迭代时间、寻优精度、稳定性等方面都优于其他智能优化算法。因此，现建立改进麻雀搜索算法优化支持向量机的井漏预测模型，实现井漏事故的预测。

1 麻雀搜索算法

SSA算法主要受到自然界中麻雀捕食和遇到危险时做出的反捕食行为的启发[8]。麻雀种群中一般包括3种麻雀：发现者、追随者和警戒者。发现者搜寻食物，它为整个麻雀种群提供食物的位置信息。追随者通过发现者提供的食物位置信息进行食物的获取，并且不断监视发现者用以争夺食物。但发现者和追随者的身份并不是固定的，它们会根据实际情况的不同，自由地切换身份。在麻雀觅食期间，如果警戒者觉察到危险时，就会向麻雀种群发出警告，种群则立即做出反捕食的行为。

发现者按式(1)进行位置更新：

(1)

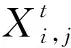
跟随者按式(2)进行位置更新：

(2)

警戒者按式(3)进行位置更新：

(3)

2 支持向量机

针对线性可分问题，使用支持向量机(support vector machine，SVM)进行分类时，旨在找到一个最优超平面将数据完全分离，并使得距离该平面最近的数据点到该平面距离最大。该过程可以理解为解决下述最优化问题。

(4)

式(4)中：i=1,2,…,l；ξi为松弛变量因子，且ξi≥0；ω为垂直于超平面的向量；b为偏移量；xi为第i个样本；yi为分类类别，取值为1或-1；C为惩罚因子，当出现错误分类时C就会增大。

为求解式(4)，首先需要引入拉格朗日函数：

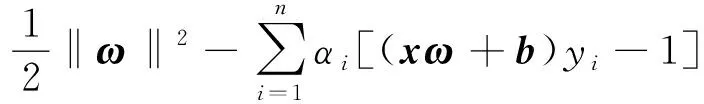
(5)

式(5)中：x为样本点构成的向量；α为拉格朗日方程的系数因子构成的向量；αi为拉格朗日方程的系数因子。

对式(5)中的ω和b分别求偏导并令其为0，解得式(4)的对偶问题：

(6)

式(6)中：aj为拉格朗日方程的系数因子；xj为第j个样本。

进一步解得，线性情况下的决策函数为

(7)

式(7)中：

为第i个拉格朗日乘子。

对于非线性问题，需要使用核函数将样本数据映射到高维空间中，从而变为线性可分。

核函数的表达式为

K(xi,xj)=φ(xi)φ(xj)

(8)

一般常使用径向基核函数，表达式为

(9)

式(9)中：g为核函数的宽度；‖x-y‖2为样本点x和样本点y之间的距离。

同理，可以得到对于非线性情况下的决策函数为

(10)

综上，使用SVM解决分类问题时，惩罚因子C和核参数g对分类结果有着较大的影响。

3 改进的麻雀搜索算法

SSA算法同样是群智能优化算法，其不可避免地存在群智能优化算法的普遍问题，即算法搜索到全局最优解附近时，种群多样性减少，容易陷入局部最优[9]。

3.1 自适应非线性惯性递减权重

分析发现者位置移动方式可以得出：发现者在寻找最佳觅食位置的过程中，移动的步长容易过大。这种“大步”的移动虽然能够在一定程度上缩短寻找最优解的时间，但这种方式容易错过全局最优解。大量的智能优化算法的研究表明，惯性权重参数对于增强全局搜索能力以及跳出局部最优解的能力起着较为积极的作用。因此，为了解决上述问题，受粒子群算法的启发，提出了一种自适应非线性惯性递减权重的策略，并将该策略引入发现者位置更新公式中。自适应非线性惯性递减权重ωm的计算公式为

(11)

式(11)中：ω1和ω2为惯性调整参数；取ω1=0.9，ω2=0.4。

引入惯性权重ωm后，发现者按照式(12)进行位置更新。

(12)

式(12)中：tmax为最大迭代次数。

根据式(11)可以看出，该自适应非线性惯性递减权重在迭代初期衰减缓慢，更加有利于进行全局搜索，确定最优解的位置，而在迭代的后期，衰减较为迅速，这有利于局部搜索并缩短找到最优解的时间。

3.2 莱维飞行策略

莱维飞行(Levy)通常以短距离和随机较长距离进行随机搜索。大量研究表明，自然界中很多动物的运动轨迹都符合莱维分布[10]。正是由于莱维飞行这种随机搜索的方式，使得其在智能优化算法寻找最优解的过程中，更加充分地进行全局搜索和局部搜索，同时更加容易跳出局部最优。

Levy的计算公式为

L=0.01s

(13)

式(13)中：s为Levy飞行步长。

(14)

式(14)中：

且

(15)

σv=1

(16)

引入Levy飞行策略的警戒者按照式(17)进行位置更新[11]。

(17)

4 ISSA算法性能测试

为验证ISSA算法在求解目标函数的极值问题中的可行性及优越性，将ISSA与SSA、GWO、GA算法在8个基准测试函数上进行对比测试。

4.1 基准测试函数

测试函数表达式如表1所示。其中f1～f3为高维单峰函数，f4～f6为高维多峰函数，f7～f8为低维多峰函数。高维单峰函数只有一个最优解，用于测试算法的收敛速度。多峰函数存在多个局部最优解，这种特性容易使算法陷入局部最优。因此，从高维和低维不同角度对算法跳出局部最优的性能进行测试。

4.2 算法性能对比分析

使用MATLAB R2019a对4种不同的算法进行对比实验。为避免单次实验出现偶然误差，进一步增强实验结果的可信度，实验中对8种基准测试函数分别独立运行30次，取平均值和标准差作为评价指标。本文研究中，统一设置种群维度为30，最大迭代次数为1 000。实验结果如表2所示。

分析表2的实验结果，可以得到：在3个高峰测试函数f1～f3中，ISSA算法的寻优精度以及稳定性均比其他算法有显著的提升，并且平均值和标准差相对于其他算法至少提升了2个数量级。在3个高维多峰函数f4～f6中，在求解f5和f6时，ISSA和SSA算法的平均值和标准差均为0，两种算法的寻优能力相同，ISSA相对于其他2种算法，寻优能力还是有显著提升。对于f4函数，ISSA算法的平均值最接近函数的最优值，并且标准差也是最小的，算法鲁棒性高。在2个低维多峰测试函数f7～f8中，对于f7的求解，ISSA在寻优精度以及稳定性方面比其他算法表现优异；在f7函数中，SSA算法在平均值和标准差方面均比ISSA算法表现良好，ISSA算法的优越性没有体现出来。但相较于其他算法有着显著提升。

表1 基准测试函数Table 1 Benchmark functions

表2 基准函数优化结果比较Table 2 Comparison of the results of benchmark function optimization

综上，ISSA算法虽然在某些情况下并不优异，但总体来看，ISSA算法在单峰和多峰、高维和低维函数上，相对于其他算法在求解精度上有一定提升，算法稳定性也更优。

5 ISSA优化SVM的井漏预测模型

5.1 ISSA优化SVM流程

将ISSA算法用于优化SVM的惩罚因子C和核参数g，对井漏事故进行预测。其优化流程图如图1所示。具体优化步骤如下。

(1)初始化种群，设置最大迭代次数tmax、种群规模D、发现者数量PD、警戒者数量SD、预警值R2、安全值ST等初始化参数。

(2)计算当前每只麻雀的适应度数值并对其进行排序，取适应度较好前PD只麻雀作为发现者。其余作为追随者。按照SD数值，在种群中随机选择一些麻雀作为警戒者。同时，记录每只麻雀的位置。

图1 ISSA优化SVM流程图Fig.1 ISSA optimized SVM flow chart

(3)根据式(12)更新发现者位置。

(4)根据式(2)更新追随者位置。

(5)根据式(17)更新警戒者位置。

(6)更新最佳适应度数值和最优位置。

(7)判断迭代是否完成，若没有完成，则重复步骤(2)。否则，输出最优参数。按照最优参数C和g构建SVM分类预测模型，输出预测结果。

5.2 ISSA优化SVM的井漏预测实现

实验所用的井漏数据来自国外某大型油田，从每日钻井报告(DDR)、每日泥浆报告(DMRs)和完井报告(FWRs)中收集了600组数据记录。其中，300组为正常情况的钻井数据，300组为发生井漏时的钻井数据。

这600组数据共有10个特征，它们分别是北向、东向、岩性、孔径、孔隙压力、破裂压力、剪切应力、凝胶强度、泵压和钻头转速。部分样本数据如表3所示。其中，岩性(地层类型)1、2、3分别代表Aghajery类型、Mishan类型以及Gachsaran 7类型。需要说明的是，这里的地层类型命名均是根据当地的地质构造决定的，因此本文不做解释。

将300组为正常情况的钻井数据，300组为发生井漏时的钻井数据，按照7∶3的比例分为训练集和测试集，进行井漏事故的分类预测。分别建立ISSA、SSA、GWO和GA算法优化SVM的分类预测模型。统一设置最大迭代次数为100次，种群数量为20。4种算法优化SVM的井漏分类预测的适应度曲线以及分类准确率结果分别如图2和图3所示。

由图2和图3可知，使用ISSA算法仅需要迭代6次，就可以达到分类准确率的最佳适应度。而SSA、GWO和GA算法分别需要迭代12次、10次和95次才可以达到各自对应的最佳适应度数值，并且均没有ISSA算法的最佳适应度数值高。这说明了ISSA相较于其他优化算法更加能够快速、准确地找出SVM的惩罚参数C和核参数g。

表3 部分样本数据Table 3 Part of the sample data

红色实线表示每次进化迭代过程中最佳适应度值；蓝色虚线表示每次进化迭代过程中种群的平均适应度值图2 4种算法优化SVM适应度曲线图Fig.2 Four algorithms to optimize SVM fitness curve

将4种算法分别用于优化SVM的惩罚参数C和核参数g，构建井漏分类预测模型，结果如表4所示。通过4种算法的对比分析，可以得出：ISSA-SVM的预测效果最好，预测准确率(Accuracy)可达到97.765 4%，相比于SSA-SVM、GWO-SVM和GA-SVM模型的预测准确率分别提高了0.558 7%、1.676%以及2.234 7%。结果表明，ISSA算法不仅在寻找最优参数方面速度快，结合SVM之后，它的分类预测准确率也比其他智能优化算法更高，ISSA算法效果显著。

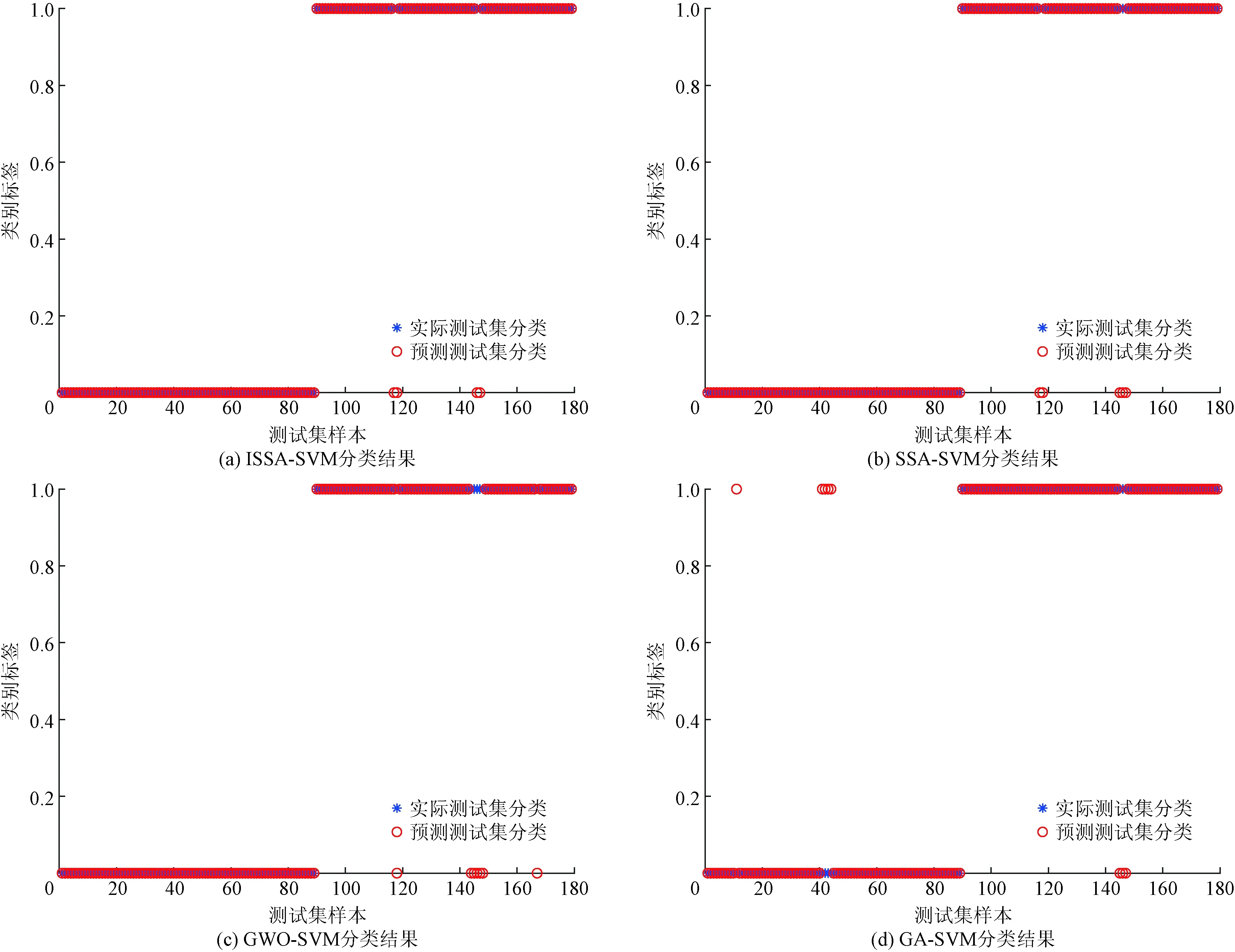
图3 4种算法优化SVM分类结果图Fig.3 Four algorithms to optimize the SVM classification result graph

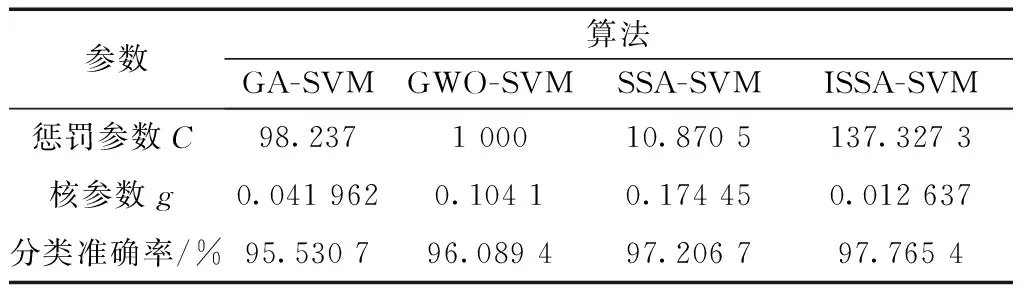
表4 4种算法对比Table 4 Comparison of four algorithms

6 结论

提出了一种ISSA算法并将其和SVM结合起来，建立了井漏事故的预测模型，得到以下结论。

(1)将ISSA算法与其他智能优化算法使用基准测试函数进行寻优性能分析，结果表明ISSA算法在收敛速度、寻优精度方面效果显著。

(2)提出的ISSA-SVM井漏预测模型，对于井漏的预测准确率可达到97.765 4%，相对于SSA-SVM、GWO-SVM以及GA-SVM井漏预测模型，在预测准确率和运算时间方面有较大的提升，鲁棒性更好。同时，为钻井过程中及时、准确的发现井漏事故，减少不必要的损失，提出了一种可行的方案，具有一定意义的参考价值。