基于t分布变异的自适应黏菌优化算法
2023-01-14李永毅张剑妹
李永毅,张剑妹,连 玮
(长治学院计算机系,山西长治 046011)
在科研、工程、经济、管理、国防乃至民生等领域中都存在优化问题。由于传统的优化算法很多属于凸优化范畴,有明确的问题描述和条件描述,已经不能满足解决复杂优化问题的需求。近年来,受自然界生物群体智能行为和自然界进化规律的启发,国内外学者提出了众多的元启发算法,其群智能优化算法是元启发算法的一种,包括一系列的优化算法,如混合蛙跳算法、飞蛾扑火优化算法、群居蜘蛛优化算法等。在AI 蓬勃发展的今天,群智能算法成为多种学科交叉融合的研究热点,并广泛应用于机器人路径规划、实时任务调度、多目标优化、分类、模式识别、信号处理、图像多阈值分割等众多领域[1-4]。2010 年2 月由日本北海道大学的Tero 教授提出黏菌的铁路网络涌现计算。2020 年,温州大学的李世民对黏菌涌现计算进行改进,提出了一种新的群智能优化算法,即黏菌优化算法(Slime mould algorithm,SMA),它是模拟自然界中黏菌觅食行为及形态变化的新型元启发式群智能优化算法[5]。黏菌算法与粒子群算法类似,也存在易陷入局部最优,收敛速度慢、寻优精度低等缺陷。提采用Levy 飞行算子改进黏菌优化算法,使得该算法的全局寻优能力增强,但经过测试发现Levy 飞行算子改进的黏菌算法,虽然使全局搜索能力增强,但寻优精度明显降低。目前国内外对其研究的文献很少。提出了一种基于t分布变异的自适应黏菌优化算法,简称tSMA 算法,来提高黏菌算法的寻优精度、收敛速度及鲁棒性。
1 基本黏菌优化算法
1.1 黏菌优化算法
黏菌优化算法灵感来自于黏菌的扩张和觅食行为。主要模拟了黏菌在觅食过程中的行为和形态变化,没有模拟黏菌完整的生命周期[5-6]。
黏菌的觅食行为:黏菌在生长及觅食过程中有许多静脉状管形成静脉状管网络,在其觅食过程,根据空气中食物的气味浓度,通过静脉状管延伸迁移寻找食物,食物浓度越高,黏菌的生物振荡器波越强,细胞质流动越快,黏菌静脉状管越粗,其离开该区域概率越低,其局部搜索能力越强;反之,食物浓度较低,黏菌的生物震荡器波减弱,细胞质流动变慢,静脉状管改变形体,静脉状管变地细而长,全局搜索模式增强,局部搜索能力减弱。黏菌的独特的生物模式(多条静脉状管)可以寻找多种食物来源。
1.2 模拟黏菌迁移模式
用数学公式表达黏菌的逼近食物行为,其数学公式如下:

1.2.1 控制参数p的计算公式

其中,i∈1,2...,n;S(i)是当前黏菌个体的适应度值,DF迭代到当前位置,获得黏菌的最佳适应度。
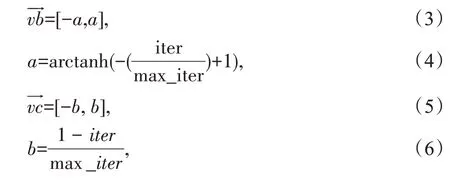
max_iter最大迭代次数,iter表示当前迭代次数。

r表示随机数,bF表示最佳适应度值,S(i)是黏菌个体的当前适应度值,wF表示黏菌个体的最坏适应度值,sort(S)表示对黏菌个体适应度值的排序序列。condition 表示黏菌个体适应度值排序在前一半的黏菌权重情况,others 表示黏菌个体适应度值排序在后一半的黏菌权重情况。
2 基于t分布的自适应黏菌优化算法tSAM
2.1 自适应t分布变异
t分布又称学生分布,含有参数自由度n,t分布曲线形态与自由度n有很大关系,当自由度较小时,曲线中间较平缓,隆起较低,随着自由度的增大,曲线中间部分逐渐隆起,当自由度为正无穷时,褪变为标准正态分布。在模拟仿真中,以迭代次数t作为自由度参数,当t较小时类似柯西变异具有较强的全局搜索能力,后期t较大时类似高斯变异具有较强的局部搜索能力。t分布的变异算子结合了高斯算子和柯西算子的优势,同时提高了算法的全局探索性和局部开发性[4-7]。
2.2 建立基于t分布的自适应黏菌优化算法tSAM
针对基本的黏菌优化算法存在的寻优精度低,收敛速度慢,易陷入局部最优等缺点,用t分布变异算子,改进迭代过程中黏菌搜索位置,当r<p时,加入t分布变异算子。
tSAM的算法设计如下:
对公式(1)进行改进,当r<p时,用t分布算子t(iter)进行扰动,更新后的公式(1),如公式(9)所示:

2.2.1tSMA伪码表示如下:

2.2.2tSMA算法流程如图1所示。

图1 tSMA算法流程
3 tSMA算法性能测试
3.1 测试函数及参数设置
为了验证tSMA算法的改进效果,对12个测试函数进行仿真,并与基本的黏菌算法SMA进行对比,在测试时,tSMA 与SMA 两种算法迭代次数、总群个数、维数等基本参数设置相同,参数设置如表1所示。
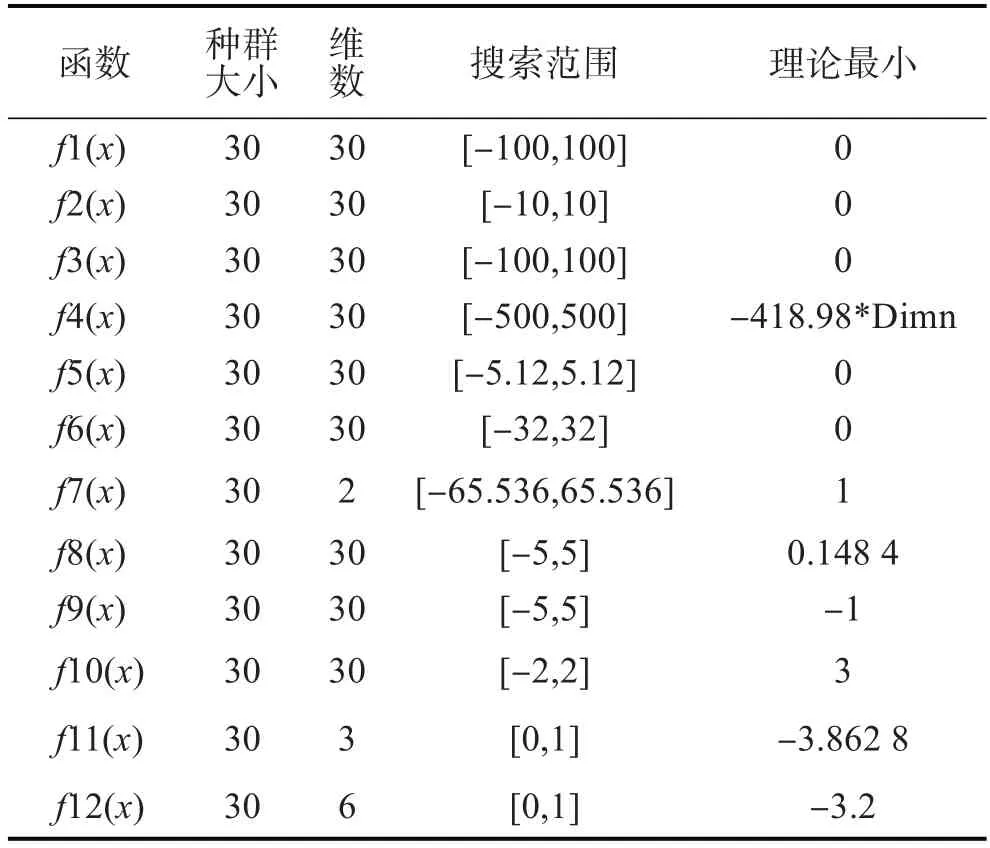
表1 测试函数的参数设置
12 个测试函数中,f1,f2,f3为单模态的基准测试函数,函数f4,f5,f6为多模态的基准测试函数,f7,f8,f9,f10,f11,f12复合基准测试函数;有的测试函数维数很高,较难找到全局最优值,有的测试函具有广泛的搜索空间,峰形高低起伏不定,有的测试函数多个极值点,很难找到全局最优值。测试函数:
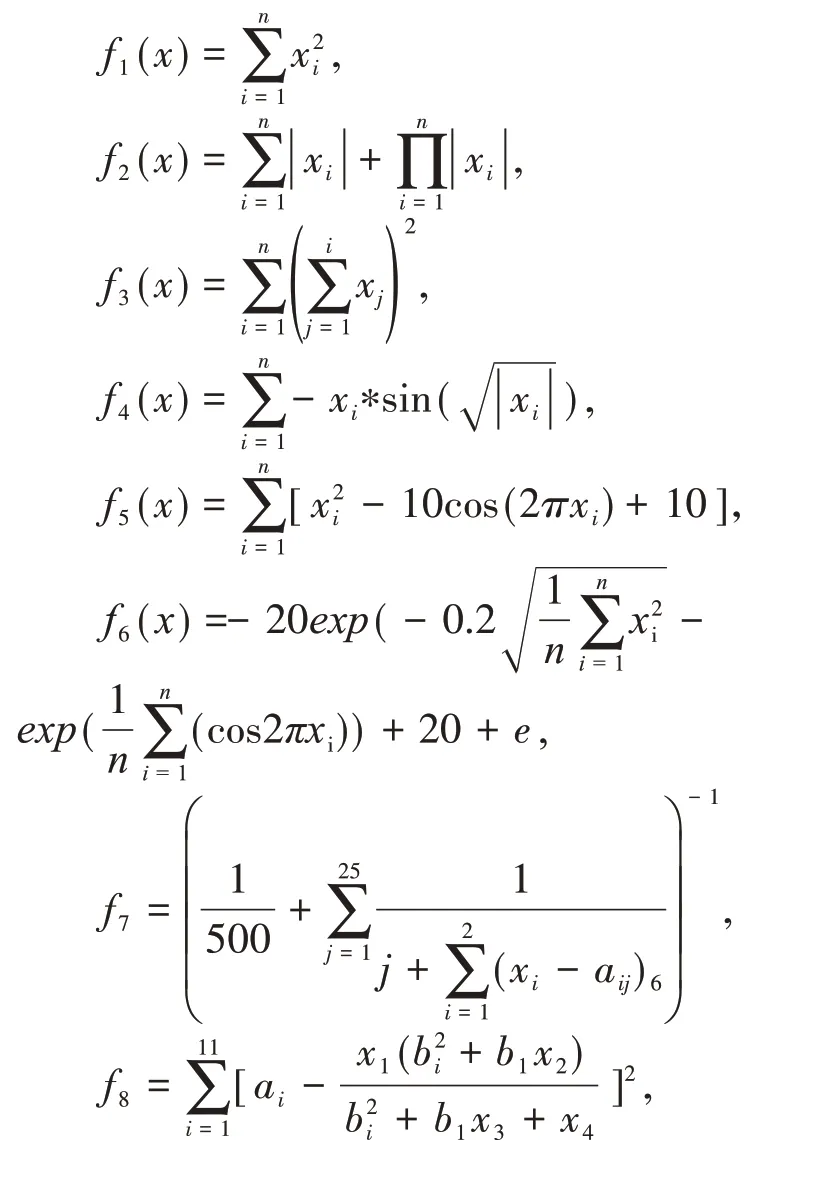
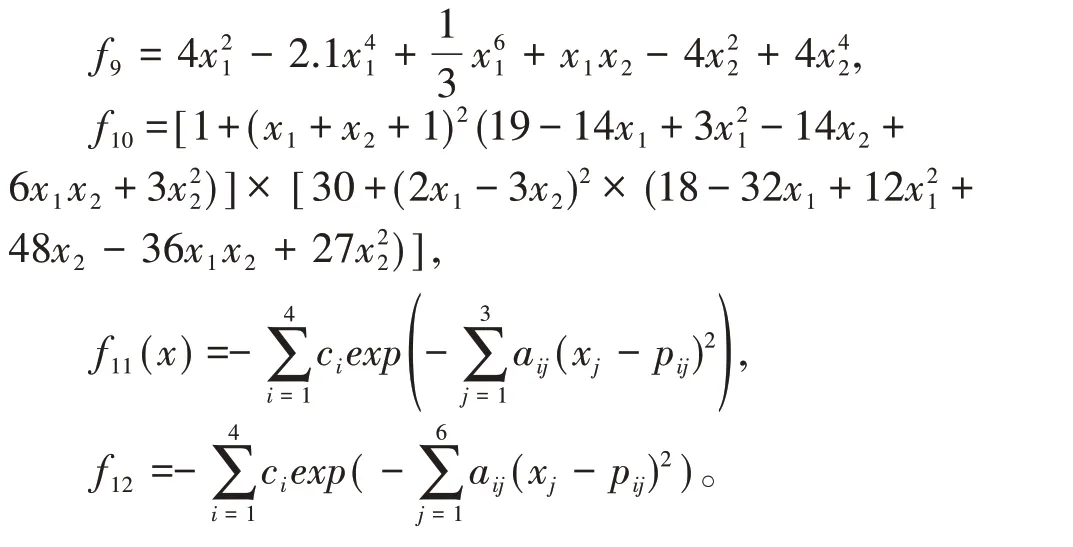
3.2 测试结果与分析
在模拟仿真测试中,tSMA 与SMA 设置相同的初始化参数,每种算法对测试函数运算15次,记录每种算法独立运行15 次的运行结果,计算运行结果的最优值、最差值、平均值、标准方差,结果如表2所示。

表2 测试函数的测试结果
测试结果表明,tSMA 与SMA两个函数都能找到或接近理论最优解,但是tSMA 算法的最优解等于或更接近理论最优解,说明tSMA 算法精度高于SMA算法;tSMA 算法测试结果的平均值等于或更接近于理论最优解,说明tSMA 算法稳定性等于或优于SMA算法,tSMA 算法测试结果的标准差小于或等于SMA算法,说明tSMA算法的鲁棒性优于或同于SMA算法。
4 tSMA 算法寻找多阈值图像分割点性能测试
4.1 基于最大熵的多阈值图像分割
多目标图像分割是图像分割领域热点工程问题。基于最大熵的单阈值图像分割算法是一种简单有效的图像分割算法,其核心思想是通过选择一个阈值,使分割后目标类与背景类的总熵最大,即信息量最大[7]。推广到多阈值分割为寻找一组阈值(t0,···,ts)使得总熵值最大,达到多目标图像分割效果。如果通过穷举遍历寻找阈值(t0,···,ts),使得总熵最大,其多阈值分割计算量极大,使用群智能优化(黏菌算法、改进黏菌)算法,寻找阈值,可以提高寻找阈值的速度。
基于最大熵的多阈值图像分割算法数学描述:
(1)计算灰度值i的统计概率:
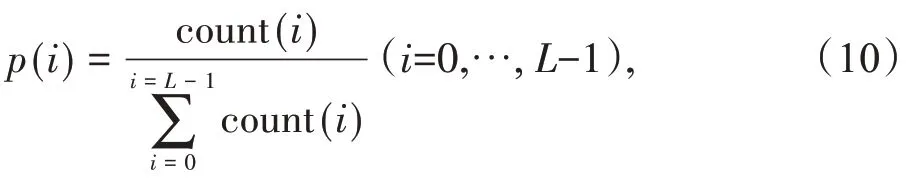
p(i)为灰度级i统计概率,i是灰度级,L是灰度级数,count(i)是灰度阶i的像素个数;tk为第k个分割点阈值。
(2)计算阈值区间的累积概率:

tk为第k个分割点阈值,

(3)计算阈值区间的熵:
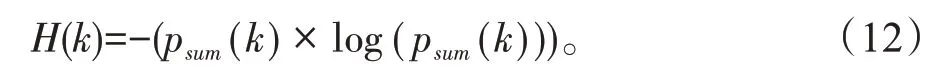
(4)计算区间熵的和:

s为阈值区间个数。
(5)计算各组阈值中最大熵:

4.2 tSMA算法寻找多阈值分割点测试
为了测试tSMA 的改进性能,对图像进行多阈值分割,寻找分割点的最优解。通过对基本的黏菌算法(SMA)、基于t分布的黏菌算法(tSMA)、莱维飞行改进的黏菌算法(LevySMA)进行测试比较。在基于最大熵的图像分割测试中,分割阈值为[0,255]之间的离散整数,而SMA、tSMA 及LevySMA 的原始算法处理的是连续数据。在测试中,对SMA、tSMA 及LevySMA 算法迁移位置进行了取整操作。通过对500*353 像素图像进行多阈值分割,设置分割阈值为5,即搜索维数为5,最大迭代次数为100,种群数为30,对SMA、tSMA 及LevySMA 算法测试15 次,测试结果如表3所示。
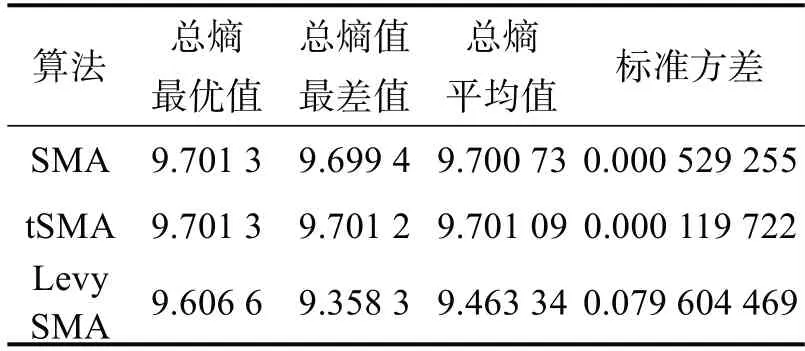
表3 基于最大熵多阈值分割测试结果
4.3 tSMA算法寻找多阈值分割点结果分析
表3 测试结果表明,基于改进的tSMA 算法标准差最小、总熵平均值最大,即tSMA算法最稳定。
为了更直观表达寻优速度,图2 给出了寻优收敛曲线,从图2 可以看出,tSMA 能够较快地找到或接近于最优解,这表明tSMA 的寻优精度及速度优于SMA 算法。说明tSMA 算法在基于最大熵的多阈值分割过程中有较好寻优性能,收敛速度快,且鲁棒性好,不易陷入局部最优解。测试发现基于莱维飞行优化SMA 算法简称LevySMA 的对于求多阈值图像分割的总熵,寻优精度及收敛性最差。
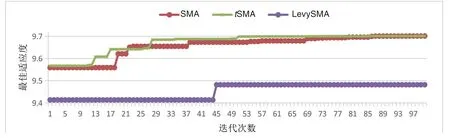
图2 三种算法在基于最大熵图像分割上的适应度进化曲线
5 结语
提出了基于t分布的自适应黏菌优化算法,通过对12个测试函数及基于最大熵的图像分割工程问题进行测试,表明基于t分布的自适应黏菌算法,有效地提高了黏菌算法的搜索能力,其寻优精度及收敛速度有所提高,鲁棒性更强。
