一类具有脉冲接种疾病模型的性态分析

张 珍

（山西大同大学数学与统计学院，山西大同 037009）

自然界中的连续渐变过程或系统中具有这样共同的特征，即系统经历一个不受本身控制的瞬间作用或系统的状态在很短的时间范围内发生快速变化，然而这个短暂的扰动时间与整个发展过程中所持续的时间相比，可以忽略不计，这种现象就称为脉冲现象。在疾病模型的研究中广泛存在，建立的模型就是对易感人群在固定时间点给与预防接种疫苗，即具有脉冲接种的传染病模型。有关脉冲接种的疾病病模型已有很多研究，见参考文献[1-7]。建立了如下的模型：

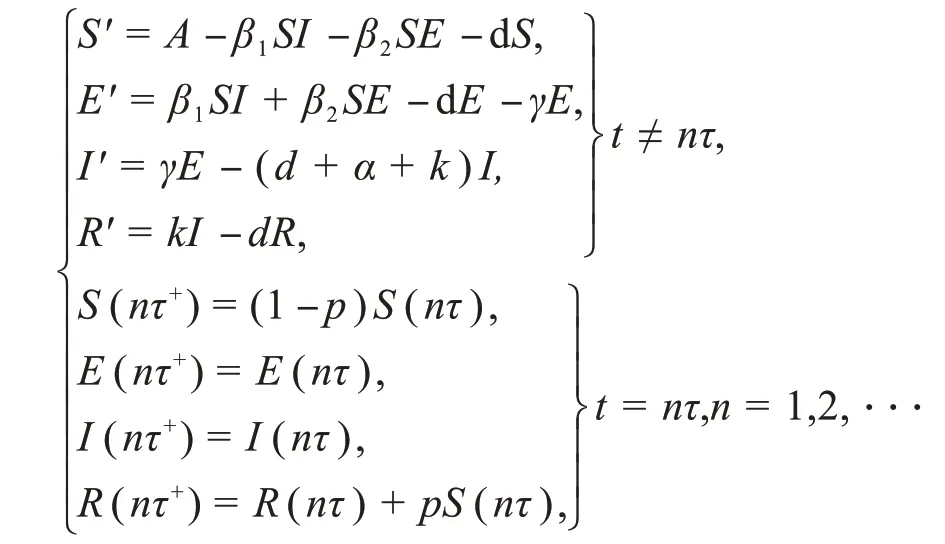
其中S(t),E(t),I(t),R(t)分别代表在t时刻易感者,潜伏者,染病者和恢复者的数量，N(t)代表t时刻总人口的数量值,且总人口数量满足方程N′=A-dN-αI。这里的A是常数移民人数，d是自然死亡率系数,α是因病死亡率系数，β1和β2分别表示S类与E类、I类的有效接触率系数，表示潜伏期，k是恢复率系数。

1 无病周期解的存在性

无病周期解如果存在，则其必须满足条件E(t)=0和I(t)=0，在这个条件下，很显然易感人群S(t)是与脉冲周期相同的一个周期函数。在t0=nτ＜t≤(n+1)τ范围内，S(t)需要满足下面的脉冲方程：

当E(t)=0，I(t)=0，不动点S*会局部表现为稳定，所以数列Sn必定收敛于S*。所以，易感人数S(t)也同时收敛于一个周期解。在t0=nτ＜t≤(n+1)τ的无病周期解为

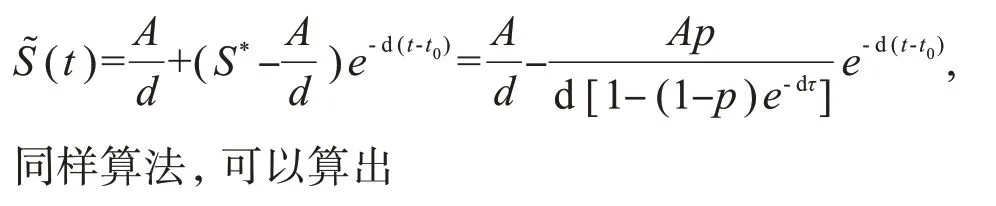
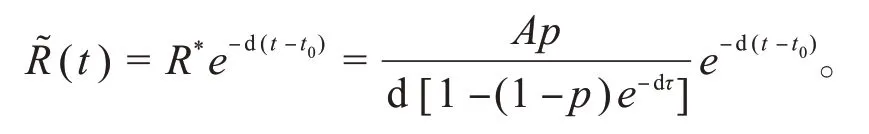
2 无病周期解的稳定性

2.1 局部稳定性

2.1.1 利用Floquet定理研究局部稳定性

无病周期解局部的稳定性可以将系统进行线性化来证明。

2.1.2 基本再生数的计算

当t=(n+1)τ+,可以推导出

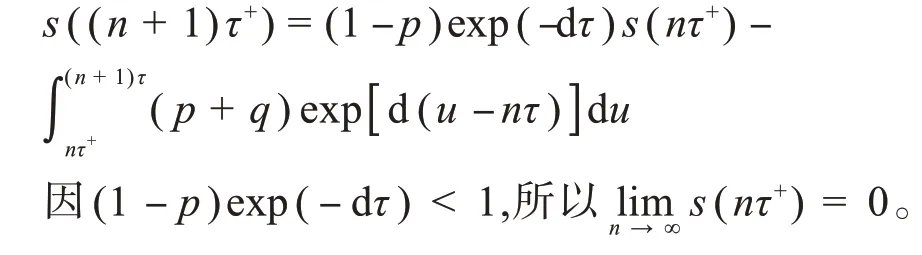
完成了无病周期解局部稳定性的证明并且很成功地算出了基本再生数。根据多次的数值模拟，得到这个疾病模型的基本再生数是完全合理的，即得到了

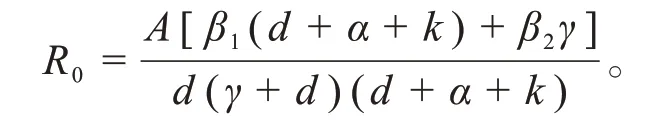
2.2 全局渐近稳定性

2.2.1 利用脉冲微分不等式引入

2.2.2 无病周期解全局稳定的结论

综合上面的证明和一系列推导，(S(t),E(t),I(t)) →((t),0,0)。

得到定理1。

定理1当基本再生数小于1 的时候，这个系统的无病周期解是全局渐近稳定的。

3 结论

在一个传染病模型中，有常数移民并且给与脉冲接种的SEIR 模型是有无病周期解并且可以算出当此SEIR模型的基本再生数

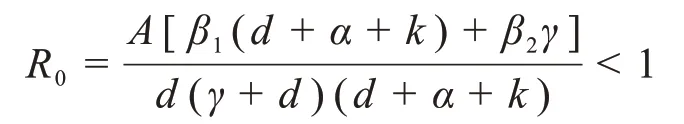
时候，无病周期解是全局渐近稳定的。所以预防接种疫苗是保护人群避免染病的有效途径，通过接种疫苗可以大幅度提高种群个体的免疫力，从而可以有效快速地控制疾病的发生以及流行。通过频闪映射、Floquet定理和脉冲微分不等式的理论知识证明了这一类传染病模型无病周期解的存在性、局部稳定性以及全局渐近稳定性。同时也说明了预防接种的重要性，它可以很有效控制疾病的恶化发展和蔓延。