欧氏平面上的Bonnesen型对称混合不等式

李 晓，周家足

(1 重庆师范大学 数学科学学院, 重庆 401331; 2 西南大学 数学与统计学院, 重庆 400715)

1 预备知识

积分几何与凸几何分析是研究凸集“空间”的几何，以(整体)微分几何、泛函分析、偏微分方程和拓扑学为基础，是现代数学中一个非常重要的研究领域。许多学者对积分几何与凸几何的发展做了贡献和开创性的工作[1-20]。文献[1-4]包含了当时积分几何与凸几何的最新成就及综述性论文。文献[5]介绍了积分几何与几何不等式的重要联系及一些新进展。文献[6-7]在对偶奥利茨-布兰-闵可夫斯基理论等方面有开创性的工作。

欧氏空间Rn中的点集K称为凸集,若∀x,y∈K,连接x和y的线段还在K内。K的凸包是所有包含K的凸集的交。凸集K和L的Minkowski和定义为

K+L={x+y:x∈K,y∈L}。

凸集K的数量积定义为

λK={λx:x∈K,λ≥0}。

∀x∈Rn,λ>0，称x+λK为凸集K的位似。域是具有非空内点的集合,凸体是紧凸域。凸集K的支持函数由Rn中的内积<·,·>定义为

hK(x)=max{:y∈K},x∈Rn。

(1)

经典的等周问题是:平面上固定周长的闭曲线中,圆所围成的区域面积最大。等周问题等价于经典的等周不等式。

命题1设K为欧氏平面R2中由简单闭曲线围成的面积为A、周长为P的域，则

P2-4πA≥0，

(2)

当且仅当K为圆盘时等号成立。

经典等周问题的证明可参见文献[8-14]。等周不等式已被推广到高维欧氏空间、流形及常曲率平面上。

从等周不等式(2)知P2-4πA刻画了平面上某域K与一圆盘的差别程度，很自然地定义欧氏平面上域K的等周亏格为

Δ2(K)=P2-4uΑ。

(3)

Bonnesen进一步深入研究平面等周不等式(2),发现了一系列形如

Δ2(K)=P2-4πA≥BK

(4)

的不等式。其中，BK是与K有关的几何量,非负，且当K为圆盘时BK=0。这类不等式是等周不等式的加强,称为Bonnesen型不等式。Bonnesen利用域的最大内切圆和最小外接圆的半径给出了加强的等周不等式，即著名的Bonnesen等周不等式[15-16]。

命题2欧氏平面R2中域K的面积A、周长P满足

P2-4πA≥π2(re-ri)2。

(5)

其中ri及re分别为K的最大内接圆半径及最小外接圆半径。等号成立当且仅当re=ri,即K为圆盘。

本文用积分几何方法，由著名的Poincaré公式和Blaschke运动基本公式估计平面上一随机凸域包含或被包含于另一凸域的包含测度，给出关于平面两凸域的对称等周不等式以及一类Bonnesen型对称等周不等式的统一证明。当其中某凸域为圆盘时，这些平面两凸域的对称等周不等式以及Bonnesen型对称等周不等式就是经典的等周不等式及Bonnesen型不等式。当考虑2维平面上的平移包含测度时，则得到了关于两平面凸域混合面积的Minkowski不等式以及一类关于两平面凸域混合面积的Bonnesen型对称混合等似不等式的统一证明。

2 积分几何中的包含测度

设Ki(i=0，1)为欧氏空间Rn中联通且道路联通的域，其边界∂Ki为简单光滑超曲面，G为Rn中的等距群，则有如下包含测度：

m{g∈G:K0⊂gK1或K0⊃gK1}=

m{g∈G:K0∩(gK1)≠∅}-

m{g∈G:∂K0∩∂(gK1)≠∅}。

(6)

m{g∈G:K0⊂gK1或K0⊃gK1}≥

(7)

因此，得到以下结论。

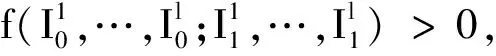
ii)如果取K0≡K1≡K,则不存在g∈G，使得K⊂gK或者K⊃gK,即

m{g∈G:K⊂gK或K⊃gK}=0。

这就导致关于域K的一个几何不等式f(I1(K),…,Il(K))≤0。这个估计包含测度的方法在2维欧氏平面时相对容易处理。

欧氏平面R2中凸域K完全由其支持函数hK(φ)唯一确定，

(8)

其中：P(x,y)∈∂K；φ是点P处外法向与x-轴的夹角。凸域K的周长P、面积A可由它的支持函数hK(φ)算出：

(9)

设Ki(i=0,1)为R2中由简单闭曲线围成的面积为Ai、周长为Pi的域,K0与K1的混合面积A01定义为

(10)

G2为R2中的刚体运动群,dg为G2的运动密度,则有Poincaré运动公式[14-15]

4P0P1，

(11)

其中n{∂K0∩∂(gK1)}为∂K0∩∂(gK1)的交点数。

设χ(K0∩(gK1))为K0∩(gK1)的Euler-Poincaré示性数,则有Blaschke运动公式

2π(A0+A1)+P0P1。

(12)

3 平面对称混合等周不等式

对于欧氏平面R2中凸域K，设t>0,凸域K的放缩tK的周长PtK和面积AtK[17]分别为

PtK=tPK,AtK=t2AK。

设Kk(k=0,1)为R2中由简单闭曲线围成的面积为Ak、周长为Pk的凸域，令

tm=max{t:t(gK1)⊆K0;g∈G2},

tM=min{t:t(gK1)⊇K0;g∈G2},

(13)

显然有tm≤tM。

若记μ为所有使得t(gK1)⊂K0或t(gK1)⊃K0的g的集合，即μ={g∈G2:t(gK1)⊂K0或t(gK1)⊃K0}，则(12)式可写成

2π(t2A1+A0)+tP0P1。

(14)

当∂K0∩∂(t(gK1))≠∅时，K0∩t(gK1)的每一连通分支的边界至少由∂K0和∂(t(gK1))的一段弧组成，因此χ(K0∩t(gK1))≤n{∂K0∩∂(t(gK1))}/2。由Poincaré运动公式(11)和Blaschke运动公式(12)可得

(15)

由不等式(15)可得一域包含另一域的充分条件[17]。

引理1设Kk(k=0,1)为R2中由简单闭曲线围成的面积为Ak、周长为Pk的凸域，则tK1包含或包含于K0的一个充分条件是

2πA1t2-P0P1t+2πA0>0。

(16)

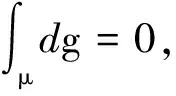
定理1设Kk(k=0,1)为R2中由简单闭曲线围成的面积为Ak、周长为Pk的凸域，则

2πA1t2-P0P1t+2πA0≤0，t∈[tm,tM],

(17)

当K0和K1为圆盘时等号成立。

考虑多项式

BK0,K1(t)=2πA1t2-P0P1t+2πA0。

(18)

显然,BK0,K1(0)>0和BK0,K1(+∞)>0。不等式(17)保证了方程BK0,K1(t)=0存在实根,即该方程根的判别式非负。因此,可以得到如下对称混合等周不等式。

定理2[17-18]设Kk(k=0,1)为R2中由简单闭曲线围成的面积为Ak、周长为Pk的凸域，则

(19)

当K0和K1为圆盘时等号成立。

自此，假设本文中所有的域均是凸的。对称混合等周不等式(19)的左边刻画了平面上两凸域与圆盘的差别程度，因此可得如下定义。

定义1设Kk(k=0,1)为欧氏平面R2中面积为Ak、周长为Pk的域,则K0与K1的对称等周亏格(symmetric isoperimetric deficit)定义为

(20)

现在考虑Bonnesen型对称混合(等周)不等式。设Kk(k=0,1)为欧氏平面R2中面积为Ak、周长为Pk的域,如果存在关于K0、K1的非负不变量B(K0,K1),使得

(21)

当K0与K1为圆盘时，B(K0,K1)=0。形如(21)的不等式称为Bonnesen型对称混合不等式。

为了得到Bonnesen型对称混合不等式, 需要如下结果。

引理2[17]设Kk(k=0,1)为R2中面积为Ak、周长为Pk的凸域，则

(22)

其中每一个等号成立当且仅当K0和K1为圆盘。

定理3设Kk(k=0,1)为R2中面积为Ak、周长为Pk的凸域，则

(23)

当K0和K1为圆盘时每一个等号都成立。

证明方程BK0,K1(t)=2πA1t2-P0P1t+2πA0=0的两个根分别为

由引理2和定理3，立即可得如下引理。

引理3设Kk(k=0,1)为R2中面积为Ak、周长为Pk的凸域，则

(24)

由不等式(24)可得如下Bonnesen型对称混合不等式。

定理4设Kk(k=0,1)为R2中面积为Ak、周长为Pk的凸域，则

(25)

(26)

(27)

当且仅当K0和K1为圆盘时等号成立。

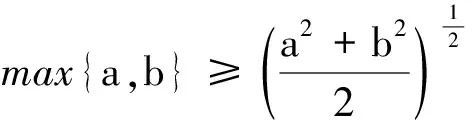
即(25)式，当且仅当K0和K1为圆盘时等号成立。

由不等式(24)和不等式ab≥cd(其中a≥c≥0,b≥d≥0)，可得

即(26)式，当且仅当K0和K1为圆盘时等号成立。

由引理2中的不等式(22)以及以上类似方法，可以证明如下定理。

定理5设Kk(k=0,1)为R2中面积为Ak、周长为Pk的凸域，则

(28)

(29)

(30)

(31)

当且仅当K0和K1为圆盘时等号成立。

注1Bonnesen型对称混合亏格以及Bonnesen型对称混合不等式由文献[17-18]得到。Bonnesen型对称混合不等式(28)、(30)是Kotlyar的Bonnesen型对称混合不等式(27)的加强。当K1为单位圆盘时，tm为K0的最大内接圆半径r，tM为K0的最小外接圆半径R,则本文中的Bonnesen型对称混合不等式就是二维平面Bonnesen型不等式[5,17,19]。