凸体覆盖泛函的估计与关于凸体覆盖的Hadwiger猜想
2023-01-13吴森林吕亚方张珂珂
吴森林, 吕亚方, 张珂珂
(中北大学 数学学院, 山西 太原 030051)
1 关于凸体覆盖的Hadwiger猜想
凸体覆盖泛函的估值是凸和离散几何中的一个自然、基本且有难度的研究问题,得到了广泛关注[1-31]。对任意整数m>1,令[m]={1,2,…,m}。Rn的一个内部非空的紧凸子集K称为一个n维凸体,所有n维凸体构成的集合记作Kn。对任意凸体K,∀c∈Rn和∀γ∈(0,1),集合
γK+c={γx+c|x∈K}
称为K的一个小位似体,γ称为该小位似体的位似系数。对任意正整数m,令
Γm(K)=inf{γ>0|∃{ci|i∈[m]}
并称Γm(K)为K的m-覆盖泛函。容易验证, 上述定义中的下确界可达。若C={ci|i∈[m]}满足
K⊆Γm(K)K+C,
则称C是K的一个m-最优构图。
当K⊂R2是欧氏平面的单位圆盘时,Γm(K)的估值问题便是经典的圆覆盖问题(disk covering problem),该问题自1916年来得到了诸多数学家的深入研究(参见文献[1]及其参考文献)。2005年以前关于凸体覆盖泛函估值的大部分结果可在文献[2]中找到。除了它本身的研究价值和理论意义外, 凸体覆盖泛函的估计问题还在关于凸体覆盖的Hadwiger猜想研究中扮演着重要角色。
猜想1(关于凸体覆盖的Hadwiger猜想, 简称为(H)猜想) 对任意n维凸体K,覆盖K所需的K内部平移的最小个数c(K)(称为凸体K的覆盖数)满足
n+1≤c(K)≤2n。
右侧等式成立当且仅当K是一个仿立方体([0,1]n在某个非奇异仿射变换下的像)。
该问题被多部专著[2-4]和多篇综述文章[5-8]反复提及, 近年来得到不少学者的研究[9-18]。但它在3维的情形仍是一个非常困难的公开问题,很大程度上是因为c(K)关于Hausdorff距离dH不连续,仅具有上半连续性,即当凸体L充分接近给定凸体K时,c(L)≤c(K)总成立。因此,即使验证了c(L)≤2n对在(Kn,dH)中稠密的凸体类均成立也无法判断c(K)≤2n,∀K∈Kn。事实上,对Kn中光滑的凸体K,c(K)=n+1总成立。
2 宗传明基于凸体覆盖泛函的估计方案
文献[19]给出了用于攻克(H)猜想的方案, 利用覆盖泛函Γm(·)关于Banach-Mazur距离dBM的连续性,克服了c(K)不连续性带来的困难。如文献[6]所述,该方案是针对(H)猜想的首个基于计算机算法和程序的解决方案。
一方面,c(K)是一个仿射不变量。因此,在研究(H)猜想时, 利用Banach-Mazur距离dBM来度量凸体之间的差异更为自然。∀K1,K2∈Kn,
T(K2)⊆γK1+x},
其中An是Rn到自身的非奇异仿射变换的全体构成的集合。显然,dBM(K1,K2)=0当且仅当K1和K2仿射等价。令~表示仿射等价关系,[K]表示K∈Kn所在的仿射等价类。对任意一对凸体K1和K2,令
dBM([K1],[K2])=dBM(K1,K2)。
不难验证(Kn/~,dBM)是一个紧度量空间。在不引起混淆的条件下,我们不区分(Kn/~,dBM)和(Kn,dBM)。
另一方面,c(K)等于覆盖K所需小位似体的最小个数[4],此处小位似体的位似系数不一定相等。因此,c(K)≤m当且仅当Γm(K)<1。于是, 验证
c(K)≤2n,∀K∈Kn
(1)
(称为(H)-猜想的不等式部分)可以转化为验证
Γ2n(K)<1,∀K∈Kn。
(2)
最后,覆盖泛函关于dBM有较好的连续性。令Γm([K])=Γm(K),∀K∈Kn。文献[19]指出Γm(·)在(Kn/~,dBM)上一致连续,文献[6]进一步证明Γm(·)是Lipschitz连续的。上述结果表明(1)式成立的充要条件为
因此,若(1)式成立,则∃ε>0使得
dBM(K,L)≤ε⟹|Γ2n(K)-Γ2n(L)|≤
令N⊆Kn为(Kn/~,dBM)的一个ε-网。亦即,∀K∈Kn,∃L∈N使得dBM(K,L)≤ε。那么
基于这些观察,宗传明提出了如下用以攻克(H)猜想的方案[30]:
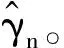
2)适当地选取ε>0并构造Kn的ε-网N。

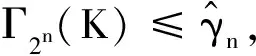
3 凸体覆盖泛函的现有估计


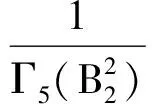
a(y)x6-b(y)x5+c(y)x4-d(y)x3+
e(y)x2-f(y)x+g(y)=0,


图1 用5个小圆盘覆盖单位圆

表1列出了一些常见凸体覆盖泛函的精确值。

表1 已知Γm(·)的精确值

可以看出,即使是对n维单纯形这样“简单”的凸体,覆盖泛函的精确值计算已非常不易。
当n≥3时,对Γm(K)估值的难度从如下结果[26]可见一斑:
一方面,上式中下标24远大于8=23; 另一方面,0.991 6…太过靠近1。即便如此, 我们仍可以取得某些特殊凸体类覆盖泛函值的较好估计。例如,宗传明[19]证明,若K∈K3是一个以平面凸体为底的凸锥,则
并且
文献[27]证明,若K∈Kn,
C1=conv(K×{0}∪{p}),
C2=conv(K×{0}∪{p,q}),
其中p,q∈Rn+1/Rn×{0}满足[p,q]∩(K×{0})≠∅,则
(3)
上述估计在很多情形下可以得到C1和C2的覆盖泛函的较好估计, 甚至得到它们的精确取值。
文献[27]还考虑了凸体K与线段L的Minkowski和K+L的覆盖泛函的取值问题。通过适当的仿射变换,不妨设平行于H=Rn-1×{0}的超平面在en和-en处支撑凸体K。令Kλ=K+λ[-u,u],其中u=en,Πu(K)为Rn至H上的正交投影。文献[28]给出了Γm(Kλ)的如下估计:
|Γm(Kλ)-Γm(K)|≤λ,∀λ≥0,
当λ>1时,可以利用Γm(Πu(K)+[-u,u])的覆盖泛函的值估计Γm(Kλ):
其中,Πu(K)+[-u,u]的覆盖泛函的取值与Γm(Πu(K))的取值密切相关。特别地,当m=c(Πu(K))时, 有
Γ2m(Πu(K)+[-u,u])=Γm(Πu(K))。
文献[28]还考虑了两个凸体直和的覆盖泛函的取值问题。设Rn是两个线性子空间L1和L2的直和,K1和K2分别为L1和L2中的凸体,并且它们均含原点。那么,∀m1,m2,有
Γm1×m2(K1⊕K2)≤max{Γm1(K1),Γm2(K2)}。
特别地,当m1=c(K1)且m2=c(K2)时,有
Γm1×m2(K1⊕K2)=max{Γm1(K1),Γm2(K2)}。
若K∈Kn关于原点O中心对称,则(Rn,‖·‖K)是一个以K为单位球的Banach空间,其中
‖·‖K=inf{λ>0|x∈λK},∀x∈Rn,
是K的Minkowski泛函。利用方向凸性模等Banach空间几何理论中的概念和结论,文献[29]给出了中心对称凸体覆盖泛函的一般估计。当K是一个中心对称的平面凸体且m=4时,给出的估计是最优的。
由于所有凸多面体构成的集族在Kn中是稠密的,其覆盖泛函的估值有重要意义。文献[9]在2016年证明:若P∈Cn是一个有m个顶点的中心对称的n维多面体,则
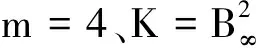
λ(x,P)=sup{λ∈[0,1]|∃ν∈V和y∈P
s.t.x=λν+(1-λ)y}。
记
λ(P)=inf{λ(x,P)|x∈P},
γ(C,P)=min{γ≥0|∃c∈Rn
s.t.C⊆c+γP},∀C⊆V。
文献[15]证明,若P∈Kn且C1,C2,…,Cm⊆V是V的一个覆盖,则
Γm(P)≤1+λ(P)max{γ(Ci,P)|i∈[m]}-
λ(P)。
(4)

∀m∈Z+。
(5)
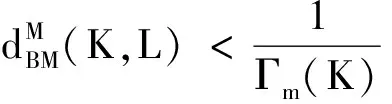
如前所述, 对很多凸体, 即使是像欧氏平面单位圆盘这样我们非常熟悉的平面凸体,当m不够特殊时,得到Γm(K)的精确值非常困难。因此, 利用计算机算法和程序来给出凸体覆盖泛函的近似值是非常必要的。早在1962年, Zahn在IBM 704用FORTRAN语言编写的程序以±0.002的精度给出了用m=2,3,…,10个等大的小圆覆盖单位圆所需的最小半径[24]。需要注意的是,Zahn的算法只能给出对应目标函数的局部最小值。
为了取得精度较高的覆盖泛函的估计, 采用类似于文献[30-31]中论述的几何分支定界法更为恰当。据我们所知, 目前尚无用于覆盖泛函估计的确定性全局优化算法。在尝试设计这种算法时,会面临两个问题:其一,随着n的增加, 估计n维凸体覆盖泛函Γ2n(K)值的算法复杂度增加很快;其二,对很多具有一定对称性的凸体K和给定的m值,K的m-最优构图并不唯一存在。只有对覆盖泛函估值有一个更全面更深刻的认识才能够最大限度地克服这些不利因素。
4 总结与展望
凸体覆盖泛函的估值是来自于凸和离散几何的一个难题, 除去自身的研究价值外, 它还在关于凸体覆盖的Hadwiger猜想的研究当中扮演着重要角色。学者们在特殊凸体覆盖泛函的精确值的计算、凸体类覆盖泛函值上界的估计等方向进行了不少研究。然而, 目前仅有极少数特殊凸体覆盖泛函的精确值已知, 只有若干性质比较简单的凸体类覆盖泛函的上界有较好估计, 尚没有用于计算凸体覆盖泛函值的确定性全局优化算法,且相应算法的设计过程面临着亟待解决的关键理论问题。
