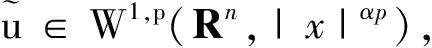一类加权Sobolev空间的嵌入研究
2023-01-13张书陶韩亚洲
张书陶,韩亚洲
(中国计量大学 理学院,浙江 杭州 310018)
在偏微分方程的研究中,Sobolev不等式、Sobolev空间发挥了重要的作用,其带来的估计、正则性、嵌入、紧性等性质,均是偏微分方程研究的有力工具[1-4]。本文研究一类加权的Sobolev空间,讨论相应的嵌入性质。
设Ω⊂Rn为开域,x=(x1,x2,…,xn)∈Ω,函数空间Lp(Ω,|x|αp)为所有满足
的函数构成,函数空间W1,p(Ω,|x|αp)由所有满足
的函数构成,并定义W1,p(Ω,|x|αp)的范数为
我们给出如下的嵌入性质。

1)存在常数C=C(n,p,α),使得

2)∀r∈(1,p*),W1,p(Ω,|x|αp)⊂⊂Lr(Ω,|x|αr)。
取参数λ、α、β满足0<λ (1) (2) 在Stein-weiss不等式[5]满足的参数条件下(具体见第2节),证明如下定理。 定理2设Ω⊂Rn为光滑紧子集,r满足 (3) 则S:Lp(Rn)→Lr(Ω)为紧映射。 (4) 其中|B1|表示Rn中单位球的体积,y=(y1,y2,…,yn)∈Rn。利用Stein-Weiss不等式[5-7](即加权的Hardy-Littlewood-Sobolev),由(4)式可得如下的一类加权Sobolev不等式。 (5) 注2对加权Sobolev不等式(5)的讨论,以及更一般的加权不等式(10)的讨论,参见文献[9]。 利用积分算子(2)的紧性(定理2)和加权Sobolev不等式(5),结合延拓算子等技巧,可给出定理1的证明。 (6) ‖|x|-βTλf‖Lq′(Rn)≤C‖|x|αf‖LP(Rn)。 (7) 两种等价形式分别为 ‖Sf(x)‖Lq′(Rn)≤C‖f‖Lp(Rn), ∀f∈Lp(Rn), (8) C‖f‖Lp(Rn)‖g‖Lq(Rn), ∀f∈Lp(Rn),g∈Lq(Rn)。 (9) 下面利用Stein-Weiss不等式给出加权Sobolev不等式的一个新证明。 (10) 证明利用Laplace算子的基本解,可得 (11) 应用Stein-Weiss不等式(7)(此时取λ=n-1),有(10)式。 (12) (13) 注4加权不等式(10)为Caffarelli-Kohn- Nirenberg(CKN)不等式[10]的特殊情形,即对应CKN不等式中a=1的情形。 定理2的证明任取Lp(Rn)中有界列{fm},由自反空间理论知存在{fm}的子列(仍记为{fm})和函数f∈Lp(Rn),使得{fm}在Lp(Rn)中弱收敛于f,下面只需要证明 (14) 即可,即证明函数数列{Sfm}在Lr(Ω)中强收敛于Sf。 若α=β=0,则Stein-weiss不等式(8)化为Hardy-Littlewood-Sobolev不等式,且Sf(x)=Tλf(x)。而Tλ:Lp(Rn)→Lr(Ω)为紧映射的证明,可以仿照文献[11]中命题2.3的证明过程,简洁起见,省略该过程。 下面讨论α、β不同时为零的情形:任取一点x∈Ω,记Rn=R1∪R2∪R3,其中 R2={y∈Rn:|y|>2|x|}, 则Sf(x)=S1f(x)+S2f(x)+S3f(x),其中 Penfolds奔富目前在中国市场上,听说过的和看到过的,包括葛兰许和Bin 707在内的奢华和旗舰系列,今年7月在澳洲首发的特瓶系列,还有这些年总是见诸报端的Ampoule等限量版,以及更加亲民的寇兰山、麦克斯和Bin系列等在内,起码有11个系列至少59款以上的产品(详见下图)。这其中,还不包括2014年3月富邑集团对外发布的,自2013年份起,市场上最热销的洛神山庄(Rawson's Retreat)系列从此摘除Penfolds品牌logo,成为旗下的一个独立品牌,其基础系列、珍藏及气泡系列,和黑金17款酒形成3个系列矩阵,开始走大单品策略。 下面分别证明{Sifm}(i=1,2,3)在Lr(Ω)中强收敛于Sif(i=1,2,3)。 由于α+β≥0,故在R1中, |x-y|α+β≤(3|x|)α+β≤3α+β2|α||x|β|y|α, 从而采用讨论α=β=0的方法证明{S1fm}在Lr(Ω)中强收敛于S1f。 从而当m→+∞时, S2f(x)。 另一方面, |S2fm(x)|≤ 由于r(n-n/p-λ-β-α)+n>0,所以W(x)∈Lr(Ω)。利用勒贝格控制收敛定理,可得{S2fm}在Lr(Ω)中强收敛于S2f。 C|x|n-(λ+β+α)p′, 注5利用(7)、(8)式的等价性可得:若函数列{|x|αfm}为Lp(Rn)的有界序列,则存在{fm}子序列(仍记为{fm})和函数f(满足|x|αf∈Lp(Rn)),使得函数列{|x|-βTλfm}在Lr(Ω)中强收敛于|x|-βTλf,其中参数r满足(3)式。 定理1的证明 ‖|x|αu‖Lp*(Rn)≤ C‖|x|αTn-1(|u|)‖Lp*(Rn)≤ C‖|x|α|u|‖Lp(Rn), (15) 结合稠密性,知(15)式∀u∈W1,p(Rn,|x|αp)均成立。 若{um(x)}为W1,p(Rn,|x|αp)的有界列,则如注5的讨论,存在{um(x)}的子列(仍记为{um(x)}),使得{|x|αTn-1(|um|)}为Lr(Ω)中的Cauchy列,从而{|x|αum(x)}为Lr(Ω)中的Cauchy列。 任取函数列{um}⊂W1,p(Ω,|x|αp)为有界列,则由第一部分的结论知,存在正常数C使得 下面只需证明:存在{um(x)}的子列(仍记为{um(x)})为Lr(Ω,|x|αp)中的Cauchy列。 利用延拓算子技巧(见文献[2]第五章),可将{um(x)}延拓为W1,p(Rn,|x|αp)中的有界函数列。利用命题3知,存在{um(x)}的子列(仍记为{um(x)}),使得{|x|αum(x)}为Lr(Ω)中的Cauchy列,即Rellich-Kondrachov型紧嵌入成立,证毕。

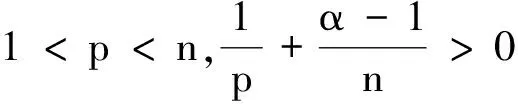
1 加权Hardy-Sobolev不等式

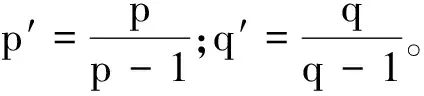





2 积分算子(2)的紧性:定理2的证明



3 Rellich-Kondrachov型紧嵌入: