具有内部存储的非均匀流动反应器模型

2023-01-13张望，魏茜，聂华

陕西师范大学学报（自然科学版） 2023年1期

张望，魏茜，聂华

(陕西师范大学数学与统计学院，陕西西安 710119)

在生态学中, 种群的动力学行为很大程度上依赖于物种间的相互作用。对流对于种群间的相互作用有着显著的影响, 因此模拟对流环境下微生物生长的流动反应器模型受到人们的关注[1-8]。通常流动反应器中营养基和微生物不仅在空间上分布不均匀,同时还受到液体流动的影响。为了描述对流环境下两种微生物种群竞争单一有限营养物的过程, Kung等[1]最早提出了以下流动反应器模型：

(1)

边界条件为

(2)

初值条件为

(3)

其中：R(x,t)、Ni(x,t)分别表示t时刻、空间位置x时营养物及竞争种群i的浓度;d为扩散系数;ν为液体流速;L为反应器的长度;R(0)为新鲜培养基浓度;ρi(R)表示种群i依赖于资源R的生长率。

文献[1]采用数值模拟的方法研究了系统(1)～(3)正平衡解的存在性, 结果表明当净比增长率曲线相交时, 系统存在正平衡态解。Ballyk等[2]在文献[1]的基础上去掉了营养物和种群随机扩散系数相同的假设, 研究了随机扩散对微生物种群生存能力的影响。关于非均匀流动反应器模型的其他研究可以参考文献[3-5]。

上述研究均假设营养的消耗和物种的生长成正比, 但忽略了一个重要的生物学现象, 即个体的养分配额可能是动态变化的。Ketchum[6]在实验中首次观察到这一有趣的生物学现象, 他发现当外部营养耗尽时, 微生物可以继续生长和分裂一段时间, 直到内部储存的营养耗尽。于是,研究者将细胞配额(即细胞内部储存的营养)引入生物数学模型, 提出了物种生长率依赖于细胞配额的浮游生物生长模型, 即具有内部储存的浮游生物生长模型,这些模型也被称为Droop模型[7]。通常,设Qi(t)表示第i个物种在t时刻的平均细胞配额, 那么依赖于细胞配额Qi的物种生长率μi(Qi)可采用如下形式描述[8-10]:

或

(4)

其中:μi∞是物种的最大生长率;(Qi-Qmin,i)+是(Qi-Qmin,i)的正部;Bi为半饱和常数。类似文献[7-9],吸收率函数可采用如下形式描述:

(5)

其中:Qmin,i≤Qi≤Qmax,i;Qmin,i表示细胞配额的临界值,低于这个阈值,物种i将停止生长;Qmax,i为最大细胞配额;amax,i是物种i的最大营养吸收率;Ki是营养吸收的半饱和系数。

Grover等[4]首次借助于具有内部存储的流动反应器模型, 研究了浮游植物在部分混合的水柱中竞争磷的生物现象。结果表明,具有较高储存能力的物种在与养分吸收和物种生长率具有优势的物种竞争过程中, 可呈现竞争排斥或共存现象。受到文献[4]的启发,本文考虑对流环境下, 具有内部存储的两种微生物种群资源依赖的生长竞争模型。为了在宏观模型(1)中引入微观细胞配额[4,11-12],令

U1(x,t)=N1(x,t)Q1(x,t),

U2(x,t)=N2(x,t)Q2(x,t),

则U1(x,t)、U2(x,t)分别分别为物种1和物种2在t时刻、空间位置x处储存的养分总量。于是,类似于文献[4,12]的推导, 带有内部存储的流动反应器模型具有如下形式:

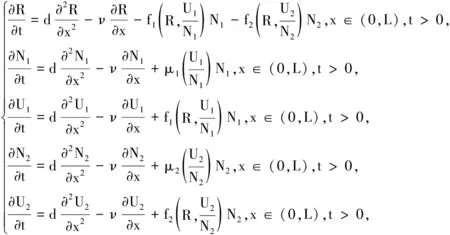
(6)

边界条件为

(7)

初值条件为

(8)

其中μi(Qi)和fi(R,Qi)分别满足(4)～(5)式。

根据实际生物意义[3-4,9]，全文总假设

根据生长率函数μi(Qi)和吸收率函数fi(R,Qi)(i=1,2)的经典形式(4)、(5)，对其做如下一般假设。

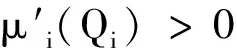
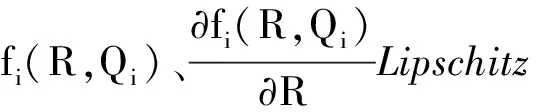
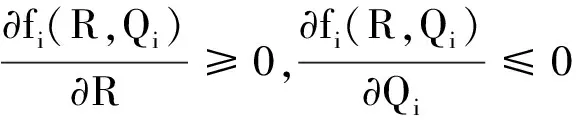
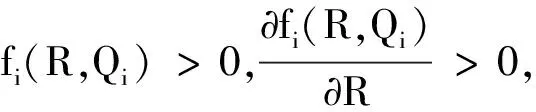
显然，μi(Qi)关于细胞配额Qi单调递增，fi(R,Qi)关于细胞配额Qi单调递减。

本文将在假设条件H0)～H2)下,研究系统(6)～(8)的动力学行为。易见,系统(6)中的比率项U1/N1和U2/N2在平凡解和半平凡解处有奇性, 这导致常用的线性化方法失效。同时对流项的引入也使得系统(6)～(8)的微分部分非自伴。为克服这些困难, 我们借助于一类非线性特征值问题来研究系统(6)～(8)的动力学行为, 建立了单种群模型关于扩散系数的阈值动力学, 给出了系统共存解存在的充分条件。

1 预备知识

首先，根据实际生物意义给出系统(6)～(8)的如下可行域：

令

W(x,t)=R(x,t)+U1(x,t)+U2(x,t),

(9)

由文献[4]易知，

(10)

(11)

下面给出系统(6)～(8)解轨线的有界性, 其证明和文献[13]中引理4.2类似,故省略。

(i)

使得

(13)

若τ=+∞，则

i=1,2,

(14)

i=1,2。

(15)

为研究系统(6)～(8)解的全局存在性,将函数μi(Ui/Ni)Ni,fi(R(x),Ui/Ni)Ni(i=1,2)做如下延拓:

(16)

(17)

定理1当系统(6)～(8)的初值属于Y时，则其在Y中产生一个半流。而且∀t>0，系统(6)～(8)存在唯一的古典解(R(·,t),N1(·,t),U1(·,t),N2(·,t),U2(·,t))∈Y。

考虑非线性特征值问题

(18)

其中：d、ν>0均为常数且h(x)∈C[0,L]；μi和fi满足H1)和H2)。

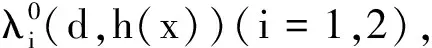
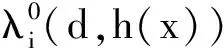
(19)

2 单种群阈值动力学

本节探讨单种群模型的一些结论。在系统(6)～(8)中令(N1,U1)=(0,0)或(N2,U2)=(0,0)，可得如下方程：

(20)

由生态学的实际意义给出系统(20)可行域为

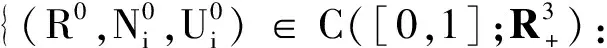
令Wi(x,t)=R(x,t)+Ui(x,t),由(20)式可得

(21)

系统(21)的可行域为

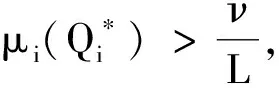
(22)

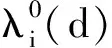
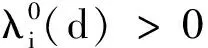
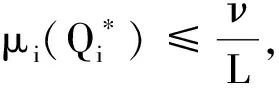
证明首先，由引理2知，非线性特征值问题(22)存在主特征值，且相应的特征值函数在锥D诱导的序下强正。下面分析该特征值的符号。

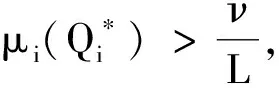
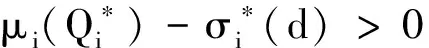
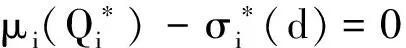
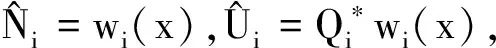
(23)

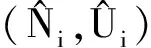
(24)

(25)

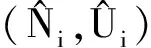
于是

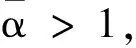
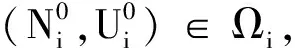
x∈[0,L]。

进一步,类似文献[13]的定理7.1,可将极限系统(21)的动力学行为提升到原系统(20),得到以下结论。

(R(0),0,0),x∈[0,L]。

3 一致持续性

本节研究系统(6)～(8)的一致持续性。注意到函数μi(Ui/Ni)Ni和fi(R,Ui/Ni)Ni(i=1,2)可分别延拓为(16)和(17)式,由定理2可知系统(6)～(8)总存在平凡的平衡态解E0(x)=(R(0),0,0,0,0)。假设

则系统(6)～(8)存在如下形式的半平凡非负平衡态解：

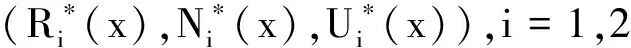
根据引理1和定理1,设

Ψt:Y→Y

为系统(6)～(8)对应的解映射。令

首先讨论E0(x)的不稳定性。

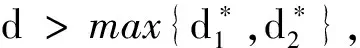
(26)

(27)

‖(R(·,t),N1(·,t),U1(·,t))-

(R(0),0,0)‖<δ0,∀t≥t0。

(28)

根据函数的连续性可知，∃δ>0使得

∀‖R(·,t)-R(0)‖<δ。

(29)

根据(28)、(29)式及系统(6)～(8)，可得

(30)

由于I0∈Y0，易得N1(·,t0)>0,U1(·,t0)>0,因此∃a1>0使得

(31)

令

(N1(·,t),U1(·,t))=

则(N1(·,t),U1(·,t))满足如下系统：

(32)

且

(33)

根据(30)～(33)式和比较原理可得，当t≥t0,x∈[0,L]时，

(N1(·,t),U1(·,t))≥(N1(·,t),U1(·,t))=

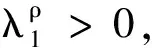
下面为了讨论Ei(x),i=1,2的不稳定性，考虑如下非线性特征值问题：

(34)

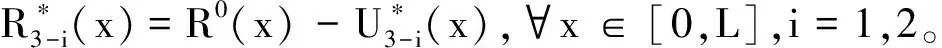
或

(35)

根据函数连续性可知∃δ>0使得

(36)

(37)

且

‖(N2(·,t),U2(·,t))-(0,0)‖<δ,

∀t≥t1。

(38)

根据(6)～(8)和(36)～(37)式，可得

(39)

因I0∈Y0,易知N2(·,t1)>0,U2(·,t1)>0。因此∃a2>0使得

(40)

令

(41)

且

(42)

根据(39)～(42)式以及比较原理，可得当t≥t1,x∈[0,L]时，

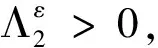
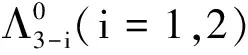
(43)

Ni(·,t,I0(·))>0,∀x∈[0,L],t>0,i=1,2,

即∀t≥0,ΨtY0⊆Y0。

令M∂={I0∈∂Y0:ΨtI0∈∂Y0,∀t≥0},w(I0)为O+(I0)={ΨtI0:t≥0}的w-极限集。首先证明

w(ψ)={E0(·)}∪{E1(·)}∪{E2(·)},

∀ψ∈M∂。

(44)

∀ψ∈M∂,t≥0可得Ψt(ψ)∈∂Y0，即N1(x,t,ψ)≡0或N2(x,t,ψ)≡0。若N1(x,t,ψ)≡0，由引理1和定理1可得,∀t≥0,U1(x,t,ψ)≡0。因此(R(·,t,ψ),N2(·,t,ψ),U2(·,t,ψ))满足

(45)

边界条件为(7)式。根据定理2可得

或

若存在一些τ0>0，使得N1(·,τ0,ψ)≢0，则根据最大值原理可知，∀t>τ0,N1(·,t,ψ)>0。由此可得∀t>τ0,N2(·,t,ψ)≡0，显然∀t>τ0,U2(·,t,ψ)≡0。由定理2可得，

或

从而(44)式得证。

定义连续函数p:Y→[0,∞)，

由最大值原理和Hopf边界引理[15]，得p-1(0,∞)⊆Y0且p满足：如果p(φ)>0或φ∈Y0且p(φ)=0，那么p(ψt(φ))>0,∀t>0。即p为对应半流Ψt:Y→Y所定义的广义距离函数[16]。

根据引理1和定理1可知，半流Ψt:Y→Y是点耗散的。显然Ψt:Y→Y，∀t>0是紧的。由文献[7]的定理3.4.8可得,Ψt:Y→Y,t≥0存在一个全局紧的吸引子。根据引理6和7易知，{Ei}在Y中孤立且Ws({Ei})∩p-1(0,∞)=∅，其中∀i=0,1,2,Ws({Ei})是{Ei}的稳定集[16]。另一方面，易得{E0(·)}∪{E1(·)}∪{E2(·)}的子集在∂Y0中均无法形成一个环。由文献[16]的定理3可得,存在一个η>0使得

即(43)式成立。