基于L1范数的全变分地震信号反褶积优化算法*
2023-01-13卢明德
卢明德
(辽河油田公司勘探开发研究院,辽宁 盘锦 124010)
0 引言
地震波在地层传播过程中会受到大地低通滤波的影响,造成高频信息严重衰减,使地震信号的分辨率大大降低。为了使地震数据能够满足构造解释和油藏勘探等要求,需要对地震资料进行高分辨率处理。反褶积算法是提高地震资料分辨率最常用的方法,在高分辨率地震资料处理中起着至关重要的作用。到目前为止,多种反褶积方法被提出,如传统的维纳(Wiener)滤波(Treitel,1974)、f-k滤波(Stewart,Schieck,1993),还有以假设地层反射信号由稀疏脉冲信号组成的常规反褶积:L1范数稀疏脉冲反褶积(Tayloretal,1979)、参数化稀疏脉冲反褶积(Lei,Terence,2000;Danilo,2006)、L1-L2范数联合反演法(王宇等,2009)、预条件共轭梯度法(朱振宇,刘洪,2005)等。L1范数稀疏脉冲反褶积对地震信号中缺失的高频信息与低频信息重建较好,但同相轴连续性较差;预条件共轭梯度法对单道处理效果不错,但执行多道反褶积时其剖面的连续性不好。总之,这些方法在提高地震信号分辨率和信噪比上具有相应的效果,但均存在一定的局限性(Hennenfentetal,2005;冯志强等,2011)。
近些年,一些新的方法被提出。如Wang等(2016)考虑反射系数的稀疏性,建立了L1范数正则化反褶积模型;潘树林等(2019)提出自适应步长的快速迭代阈值收缩法(Beck,Teboulle,2009),解决稀疏脉冲反褶积问题,具有超线性收敛速率;Pan等(2019)提出了自适应的频率域Bregman稀疏脉冲反褶积算法,在抗噪、自适应与计算效率方面体现了较好的优势;马涛等(2020)实现了利用可控震源力信号反褶积方法提取可控震源单炮记录;杜鑫等(2021)通过优选常规地震勘探反褶积处理方法,改进常规地震数据处理流程,使地震勘探的分辨率可以满足城市地下空间调查的精度要求;张联海等(2021)提出由数据驱动的深度卷积神经网络模型来解决地震反射信号的稀疏反褶积问题。然而,目前大多反褶积方法最主要的限制在于假设条件的需要,以及提高分辨率的同时也会提高噪声的能量,降低了地震信号的信噪比。因此,研究出能同时提高分辨率、衰减噪声,并保持剖面连续性的反褶积方法仍具挑战性。
目前,基于全变分(Total Variation,TV)的理论(Rudinetal,1992)在信号去噪、医学信号重建、运动成像等信号处理领域得到了广泛应用(牛和明等,2011;石明珠等,2011;Chenetal,2010)。对于全变分模型范数的选取,L2范数一般只针对高斯噪声有效,然而实际地震信号同时会遭受到异常值等非高斯噪声的攻击。针对此种情况,L1范数能表现出较好的性能,并易于求解(Rudinetal,1992;Yangetal,2009b)。因此,基于数学范数最优化理论,本文提出一种L1范数的全变分地震信号反褶积优化算法(L1TV-SSD),并将该算法对合成信号和野外采集地震数据进行实验。
1 L1范数全变分地震信号反褶积(L1TV-SSD)
1.1 L1TV地震信号重建模型构建
假设地震记录的道数为n,各地震道包含的采样点数为m,那么总采样点数为n×m个元素。地震数据矩阵r可表示为:
(1)
令x*=vec(r)为矩阵r的拉伸向量,即x*∈Rnm;w∈Rnm是地震数据中的随机噪声,K∈Rnm×nm是褶积算子,f∈Rnm是实际地震信号,满足如下关系:
f=Kx*+w
(2)
在K给定的前提下,从含噪声的实际地震信号f中重建初始地震信号x*,即重建地震信号可视为反褶积和去噪同时处理。若K为单位算子,则此操作仅为去噪处理。依据Rudin等(1992),Vogel和Oman(1998)研究,=Kx-f=1≈=w=1,即使用重建初始地震信号x*可对公式(3)进行最小化处理:
Φfid(x,f)==kx-f=1
(3)
式中:=·=1为L1范数;Φfid(x,f)是噪声信号的保真项。
本文目标是从f中重建x*,但此过程对噪声w过于敏感,重建x*存在不稳定性。为解决此问题,需融入TV正则项(Rudinetal,1992;Wangetal,2008),即TV的离散形式:
(4)
式中:=·=2为L2范数;Di为局部有限差分算子;Dix∈R2为x在采样点i处垂直方向与水平方向的一阶有限差分。地震信号的重建过程为求解式(5)的最小化(Yangetal,2009a):
(5)
即地震信号的重建模型为:
(6)
式中:μ>0为平衡二者的参数。注意:x*是理论上的真实地震信号数据;x为被恢复后的地震数据。本文通过交替方向乘子法(ADMM)求解式(6)。
1.2 交替方向乘子法(ADMM)
ADMM的基本思想需追溯到Gabay和Mercier(1976)的研究,即令θ1(·)和θ2(·)为凸函数,A为连续的线性算子,则最小化能量函数为:
(7)
通过引入辅助变量v,式(7)可等价转换为:
(8)
式(8)的增广Lagrangian函数为(Gabay,Mercier,1976):
(9)
式中:λ和β为增广Lagrangian求解最优化的引入参数。因此,交替方向乘子法的迭代解如下:
(10)
式(10)的交替最小化迭代思想为:首先由初始化(vk,λk)获取uk+1,再使用uk+1和λk获取vk+1,从而可得到λk+1。最后,利用交替方向最小化的多次优化来获得恢复的地震信号。
1.3 L1TV地震信号重建及算法
首先,将式(6)转化成式(8)形式,可表示为:
(11)
式中:y=(y1;y2)∈R2nm,y1和y2是长度为n×m维向量, 满足((y1)i;(y2)i)=yi∈R2。利用二次罚函数法把式(11)转成无约束优化函数形式:
(12)
式中:β≫0为罚参数。通过ADMM对式(12)进行求解(初始x=xk,λ=λk),可得到:
(13)
式中:LA(x,y,λ)为式(12)的增广Lagrangian函数:
(14)
式中:λi为R2空间中的向量。根据Wang等(2008)和Yang等(2009a)研究,式(13)中argminyLA(xk,y,λk)等价于如下形式:
(i=1,…,n·m)
(15)
式(15)通过二维收缩来求解(Wangetal,2008;Yangetal,2009a):
(16)
在固定yk+1和λk的基础上,通过最小二乘法求解式(13)中argminxLA(x,yk+1,λk):
(17)

最后,由式(18)更新λ:
λk+1=λk-γβ(yk+1-Dxk+1)
(18)

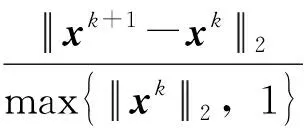
2 实验结果与分析
2.1 合成地震记录实验
为了对L1TV-SSD算法进行有效性评价,将其应用于合成地震记录上进行实验,并与维纳滤波和拉普拉斯滤波结果进行比较。实验中选取参数为:γ=1.618,ε=10-3,罚参数β=10;为了使地震信号重建获得最好的结果,不同的地震信号数据,μ值取值不同,范围一般在(0,60]。
采用信噪比(Signal-Noise Ratio,简称SNR)来评价地震信号重建的质量,SNR定义为:
(19)
式中:x*为原始地震记录;E(x*)为x*的均值强度;x是重建后的地震信号数据;SNR单位为dB。

(a)原始合成地震记录
原始合成地震记录主频为35 Hz、1 ms采样、共150道,每道采样点数为600,地震波为雷克子波(图1a)。使用高斯核函数(标准差σ=2)与原始地震记录褶积得到数据的SNR为7.69 dB。从图1b中可以看出,箭头指向处主频降低。使用L1TV-SSD算法对图1b数据进行处理(μ=5),箭头指向处的分辨率明显提高,SNR值提高至13.88 dB(图1c)。图1d为SNR、优化目标函数值与L1TV-SSD算法迭代数的关系曲线,在迭代48次后SNR持续增加,优化目标函数值随迭代次数的增加一直逐渐降低,在近140次时降到最低。
图1e与f分别是使用维纳滤波与拉普拉斯滤波的处理结果,SNR分别为10.42 dB与9.13 dB。维纳滤波的处理效果提升不大,拉普拉斯滤波处理结果其主频有所提高,但多了噪声。综上,L1TV-SSD算法获得了较好的处理效果。
对原始地震记录(图2a)进行加噪处理后进行实验。使用高斯核函数和原始地震记录进行褶积,再通过Matlab中“randn”函数增加随机噪声的数据如图2b所示。高斯核函数的标准差σ=1.5,随机噪声系数设置为0.02。使用L1TV-SSD算法对图2b数据进行处理(μ=4),从图2c可明显看出,L1TV-SSD算法有效地衰减了随机噪声,提高了分辨率,SNR由5.79 dB增至11.98 dB。从图2d可以看出,随着迭代次数的增加,SNR不断提升,而目标函数值不断降低。对于维纳滤波结果(图2e)和拉普拉斯滤波结果(图2f),尽管二者的同相轴较图2b清晰,但增加了较多的噪声,使得信噪比下降,这表明这两种结果极易受噪声的影响。图3为加噪声数据、维纳滤波方法和本文方法处理结果的第125道频谱对比图。从图中可以看到,L1TV-SSD算法提高了子波的主频,拓宽了有效频带,起到了反褶积的作用,高频随机噪声同时也得到了较好的压制;而维纳滤波方法引入了较多的随机噪声,降低了子波的主频。

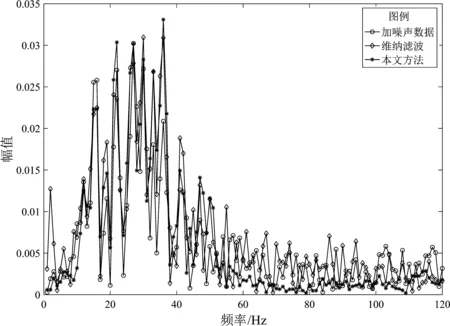
图3 加噪声数据、维纳滤波方法和本文方法处理结果的第125道频谱对比Fig.3 Comparison between the spectrums of the 125thtrace respectively obtained by the noisy data method,the Wiener filtering method and the proposedmethod in this paper
对原始地震记录(图4a)增加较强的随机噪声,其数据如图4b所示,随机噪声系数为0.15,用于褶积的高斯核函数的标准差σ=1.5。由于维纳滤波和拉普拉斯滤波受噪声影响太大,因此,本文不做讨论。图4c为L1TV-SSD算法的处理结果(μ=4),从图中明显可看出,即使在信号受到较强噪声污染时,也可以获得不错的处理结果,
SNR由-8.48 dB增至7.60 dB。同样,从图4d可以看到,随着迭代次数的增加,SNR不断提升,而优化目标函数值不断降低。

2.2 实际资料处理
为了更好地说明L1TV-SSD算法的适用性,将其应用于辽河某地区三维地震资料处理中。图5a为一初始叠加剖面,信噪比较低;图5b为L1TV-SSD算法处理结果;图5c和d分别为应用GeoEast软件的径向预测滤波(RadiPredicFilt)和随机噪声衰减(RNA)两个模块的处理结果。3种方法的对比剖面分析表明:L1TV-SSD算法对原始叠加剖面的背景噪声具有更好的压制效果,并且对模糊的同相轴有更好的处理效果,使其连续性增强,同相轴更加清晰,层间信息更加丰富,整体的分辨率明显提高。从RadiPredicFilt和RNA两个模块来看,RNA在噪声衰减以及细节的清晰度方面要优于RadiPredicFilt。

为了进一步验证L1TV-SSD算法的有效性,选取实际的CDP道集(图6a)进行处理,从图6a可以看出,实际资料存在很强的随机噪声,对有效信号造成了强烈的干扰。图6b~d分别为使用L1TV-SSD算法、径向预测滤波(RadiPredicFilt)和随机噪声衰减(RNA)模块对实际的CDP道集处理的结果。从处理效果来看,3种方法均有效地压制了随机噪声,L1TV-SSD算法有其更好的压制效果,突显出来的细节信息要优于其它两种方法。
3 结论
地震信号质量的提高可为成像的精确性奠定基础。本文提出一种提升地震信号分辨率和信噪比的新算法——L1TV-SSD算法,为了对该算法进行有效性评价,将其应用于合成地震记录和辽河凹陷野外采集数据进行实验,主要结论如下:
(1)基于L1范数全变分理论构建地震信号重建模型,通过交替方向乘子法解决转化后最小化问题,设计地震信号优化处理算法,同时实现反褶积与去噪处理。
(2)使用L1TV-SSD算法、维纳滤波和拉普拉斯滤波对合成数据处理后发现:维纳滤波的处理效果提升不大,拉普拉斯滤波处理结果其主频有所提高,但多了噪声,而L1TV-SSD算法处理效果分辨率明显提高。
(3)从对含噪声的合成地震处理结果发现:对于辽河凹陷野外采集的数据,L1TV-SSD算法提高了子波的主频,有效提高了地震资料的分辨率和信噪比。
(4)本文提出的方法避免了常规地震信号反褶积和去噪相互影响的不足,提供了新的处理思路。
