基于随机聚集维数分析地震对乡村聚落分布演变的影响*——以云南丽江、武定和鲁甸为例

柳元程，王培茗，李知远

(云南大学 建筑与规划学院，云南 昆明 650500)

0 引言

地震对人类居住地，尤其是对乡村聚落会造成巨大破坏(林均岐，刘金龙，2021；刘绍昌等，2021)。乡村聚落的分布形式因聚落内部分或全部房屋建筑倒塌重建而发生改变(齐文华等，2012)，聚落新的分布特征是村民在趋利避害思想引导下，自发选择相对安全的区域进行建设而形成的(任晓蕾，2012)。因此，研究地震前后乡村聚落的演变特征对了解村庄选址的安全性以及未来乡村聚落布局优化及聚落建设安全性有重要意义。

乡村聚落作为农村居民生产、生活的聚居场所(马利邦等，2022；张慧等，2022)，其研究主要聚焦于分布特征(刘志林等，2021)、演变特征(纪惠文，查小春，2022)、优化布局(毛琦红，2021)、驱动机制(杨斌等，2021)、空间重构(金利霞等，2020)等方面，并且从定性逐渐转向定量研究。乡村聚落分布的演变一直是国内外学者研究的热点，研究区域涵盖平原、山地丘陵、沿海等，研究内容包括演变格局、演变机制、演变过程等，演变驱动因素涉及社会经济因素、区位因素、自然因素、政策因素的复合影响。其中关于自然因素下的灾害因素导致的乡村聚落演变研究，国外学者主要关注洪水(Karunarathne，2021)、气候(Nichols，2019)、滑坡(Vaculisteanuetal，2019)灾害下的聚落演变机制，方法上多采用深入访谈、问卷调查等定性分析法，研究灾害后基于原住居民个人偏好、生计变化、政府导向等的空间格局变化，也有学者从环境心理学和自然灾害学的角度分析聚落演变带来的生态风险(Wolsko，Marino，2016)。国内学者针对自然灾害因素对乡村聚落的分布、演变作用机制的研究不多，主要涉及滑坡(蒋海香，2019)、泥石流(张恒曼，2019)、地震(张堃，2020)等地质灾害，研究地区多集中在生态环境脆弱、地质灾害频发的高原山地区域。研究方法上，随着空间计量学的发展，多结合3S技术、景观格局指数等定量分析方法对聚落的演变形态、规模、分布特征进行分析(马晓蓉，查小春，2021)，缓冲区分析、Logistic回归分析等方法被应用于探究灾害的驱动机制。可见，国内外学者对自然灾害因素方面的研究较少涉及地震灾害影响下的乡村聚落分布特征的演变，且鲜有对比分析地震前后极震区内乡村聚落分布特征的研究。本文以云南1995年武定6.5级、1996年丽江7.0级、2014年鲁甸6.5级3次地震为研究对象，运用GIS空间分析、分形理论的随机聚集维数，探讨了地震对极震区内乡村聚落分布特征的演变，以期为地震后的乡村聚落分布特征优化及聚落建设提供建议。

1 数据来源与研究思路

1.1 数据来源

本文数据来源于以下几个方面：①地震带相关信息来自于《云南第四纪活动断裂暨<云南第四纪活动断裂分布图>》(安晓文，常祖峰，2018)、《云南地区强震(M≥6)研究》(毛玉平，韩新民，2003)、《云南地震灾害与地震应急》(李永强，王景来，2003)、《1988年云南澜沧—耿马地震》(姜葵，1993)等；②村落及地形数据来自于地理空间数据云平台，包含1994年武定、1995年丽江、1998年武定、1999年丽江、2013年鲁甸、2017年鲁甸的ASTER GEDM数字地形数据以及Landsat 8 OLI TIRS遥感卫星影像(分辨率30 m)。

1.2 研究思路

国内对于地震极震区的标准定义为：震中附近振动烈度最高，同时破坏比也最严重的区域(李璐等，2018)，本文在该基础上主要研究地震烈度Ⅸ度及以上区域内乡村聚落的分布演变特征。

分形理论就是根据分形体本身的自相似性和无标度性来解决离散随机分布的问题。杨秀春和朱晓华(2003)通过研究中国大陆地震点状灾害的分形特征，证明了其分布的自相似性和无规则性，而极震区内乡村聚落斑块是系统自组织发展的体现，属点状系统，可通过分形理论来测算其分布特征规律(管驰明等，2001)，虽然研究对象(乡村聚落斑块、地震灾害点)属性不同，但其分布都具有无标度和自相似性的特征，可以应用分形理论进行研究。

分形理论的聚集维数反映的是点状要素(乡村聚落斑块)围绕地震震中的随机聚集特征，即乡村聚落斑块分布从地震震中向周边区域的密度变化特征，反映了乡村聚落系统空间结构的紧致性及扩散性，其分维值一般用D表示。通过对回转半径和乡村聚落斑块分布进行相应的数学计算统计，可以得出确切的分维值D：当D<2时，乡村聚落斑块的空间分布从震中向周围是密度递减的，即离震中越远，乡村聚落斑块呈现由密集向稀疏的分布趋势；当D=2时，乡村聚落斑块在半径方向上是均匀变化的，即自震中至外围无任何密度上的变化；当D>2时，则从震中向周围是密度递增的，即离震中越远，乡村聚落斑块分布越密集。

本文拟通过对比1995年武定6.5级、1996年丽江7.0级、2014年鲁甸6.5级地震极震区范围内地震前1年、地震后第3年乡村聚落斑块变化和随机聚集维数数据，分析得出极震区乡村聚落的演变规律(图1)。

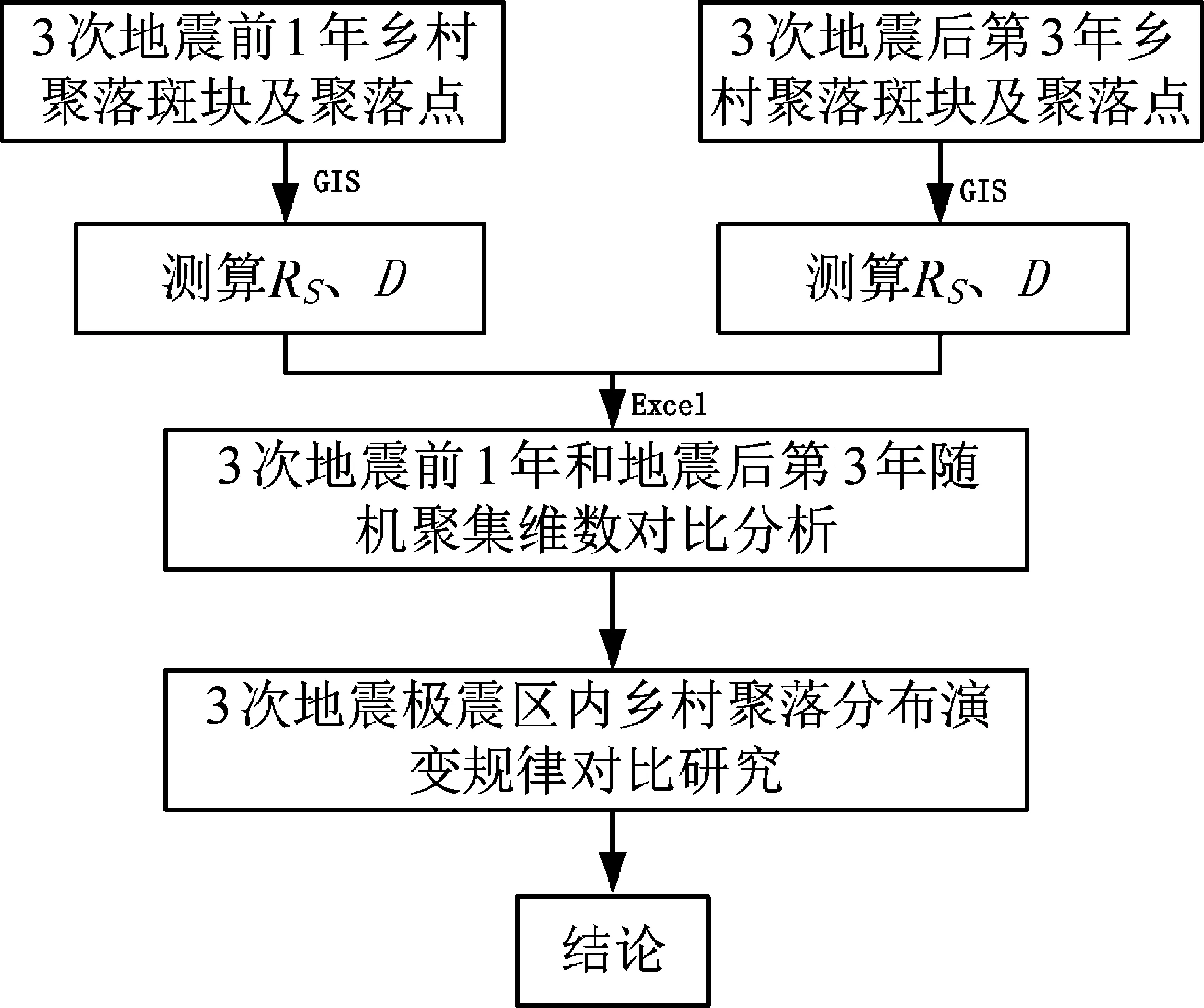
图1 本文研究思路

1.3 研究方法

假定极震区内乡村聚落按照某种自相似性规则围绕着空间系统中的首位空间呈凝聚态或者分散态分布，且是均匀变化的，满足这些条件就可以根据分形中几何测度来确定在以r为半径的圆内乡村聚落点数目N(r)和对应半径之间的关系，根据刘继生和陈彦光(1999)提出的分形维数测算方法可得到：

N(r)∝rDf

(1)

式中：Df为分维数；N(r)为乡村居民点数目；r为乡村居民点距地震中心点的欧氏距离(半径)。考虑到半径r的单位取值会影响分维值，故将其转化为平均半径：

(2)

由此可得一般的分维关系为：

RS∝S1/D

(3)

式中：S为乡村居民点数目；ri为第i个乡村居民点距离地震中心点的欧氏距离或者半径。对式(2)中的S、RS值求对数，可得到分形体乡村聚落欧氏几何下的一系列{S1，S2，…，Sn}和{R1，R2，…，Rn}，把(RS，S)在双对数坐标图上描绘成散点图，并通过最小二乘法得出随机聚集维数D。

2 实证研究

2.1 随机聚集维数实际测算

通过ArcGIS处理得到1995年武定，1996年丽江和2014年鲁甸3次地震前1年和震后第3年极震区内的乡村聚落斑块图(图2)，通过3次地震前后极震区内各乡村聚落随机聚集维数数据分别绘制地震前后乡村聚落随机聚集维数对比图(图3)。

图2 1995年武定6.5级(a)、1996年丽江7.0级(b)、2014年鲁甸6.5级(c)地震前后极震区乡村聚落斑块对比Fig.2 Rural settlements in the meizoseismal areas before and after the 1995 Wuding MS6.5 earthquake(a)，the 1996 Lijiang MS7.0 earthquake(b)，and the 2014 Ludian MS6.5 earthquake(c)

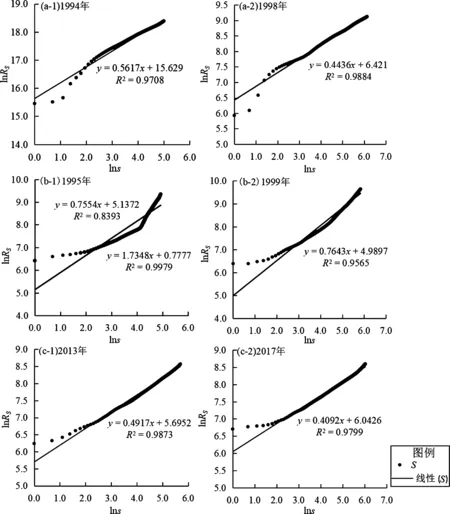
图3 1995年武定6.5级(a)、1996年丽江7.0级(b)、2014年鲁甸6.5级(c)地震前后极震区乡村聚落随机聚集特征Fig.3 Random gathering characteristics of the rural settlements in the meizoseismal areas beforeand after the 1995 Wuding MS6.5 earthquake(a)，the 1996 Lijiang MS7.0 earthquake(b)，and the 2014 Ludian MS6.5 earthquake(c)

从图2可以看出，3次地震后极震区内乡村聚落数量明显比震前增多。根据GIS统计计算可知：武定地震极震区乡村聚落点在1994年共有148个，而震后于1998年增加至461个，约为震前的3倍；丽江地震极震区乡村聚落点在1995年共有138个，而震后增加至341个，约为震前的3倍；鲁甸地震极震区乡村聚落点在2013年共有297个，而震后于2017年增加至413个，约为震前的1.5倍。

由图3a可得出：①1994和1998年武定地震极震区乡村聚落点对数坐标图均呈现一次函数形式(1994年R2=0.970 8，1998年R2=0.988 4，均小于1)，对其函数进行线性拟合，系统也均呈现一分形特征，即通过一次函数形式反映一分形特征。一次函数无拐点，根据随机聚集维数的分形特征及拐点数划分分形结构，一分形接近线性且无拐点，说明武定地震前后其乡村聚落分形表象并未产生变化；②1994、1998年武定地震极震区乡村聚落点对数坐标图的系统一分形的分维度值D分别为1.780 3<2，2.254 3>2。

由图3b可得出：①丽江地震前的1995年极震区乡村聚落点对数坐标图呈现二次函数形式(R2=0.839 3、R2=0.997 9，均小于1)，而震后的1999年呈现一次函数形式(R2=0.956 5，小于1)；②对1995年丽江地震前极震区乡村聚落点对数坐标图中拐点处进行分段，然后对其分段函数分别进行线性拟合，系统呈二分形的特征，乡村聚落序号0～69段为第一个分形特征(D1=1.323 8<2)，乡村聚落序号69～138段为第二个分形特征(D2=0.576 4<2)。对地震后1999年极震区乡村聚落点对数坐标图中函数进行线性拟合，可见系统呈一分形的特征(D=1.308 4<2)。

由图3c可得出：①鲁甸地震极震区乡村聚落点对数坐标图在震前的2013年及震后的2017年均呈现一次函数形式(2013年R=0.987 3、2017年R22=0.979 9，均小于1)，对其函数进行线性拟合，系统也均呈现一分形特征，说明鲁甸地震前后其乡村聚落分形表象并未产生变化。②2013、2017年鲁甸地震极震区乡村聚落点对数坐标图，其系统一分形的分维度值D分别为2.033 7≈2，2.443 7>2。

2.2 极震区乡村聚落分布演变规律分析

鲁甸地震后极震区乡村聚落数增加幅度明显低于武定、丽江地震，其主要原因有：震后村落民房建筑异地迁建后，在遥感影像中会形成新的乡村聚落斑块。根据云南民房恢复重建的模式可知：异地迁建的组织形式分为“统一规划、集中自建”“统一规划、分户自建”和“指导性规划、分户自建”3种，从而理论上地震后极震区内乡村聚落数相对于地震之前通常会增加。由于2006年云南省开始实行“民居防震保安工程”(刘星文，2013)，指派专业技术人员对民居进行过简易抗震处理，因此2014年鲁甸震后乡村聚落数增加幅度有所下降。

1995年武定地震极震区乡村聚落随机聚集维数分维值由地震之前的1.780 3变到了地震后的2.254 3，极震区乡村聚落由地震之前围绕地震震中相对集聚分布的状态变成震后相对离散分布的状态，主要原因有：震中位置地震活动强度以及烈度大，造成村落破损倒塌情况严重，倒塌的村落民房远离震中的搬迁数也相应较多。武定地震震中位于海拔2 000 m以上的山区，山形陡峭、切割剧烈，地形复杂。地震后，震中附近地区并不适合重建村落民房，因而倒塌民房多数远离震中搬迁。

1996年丽江地震极震区乡村聚落随机聚集维数分形特征由地震之前的二分形结构变为震后的一分形结构，极震区乡村聚落由震前围绕地震震中相对高度集聚的状态变成震后相对低度集聚的状态，主要原因是：震中位于丽江县城以北，靠近县城的乡村聚落民房抗震标准以及地基基础强度都较高，地震后，乡村聚落民房倒塌数较少，而靠近城区、经济发达的地区，一般会原地重建，所以随机聚集维数分维值变化不大。

2014年鲁甸地震极震区乡村聚落随机聚集维数分维值由震前的2.033 7变到了震后的2.443 7，极震区乡村聚落由震前围绕地震中心点相对均衡分布的状态变成震后相对离散分布的状态。主要原因是：震中位置地震活动强度以及烈度大，造成村落民房破损倒塌情况严重，倒塌的村落民房远离震中的搬迁数也相应较多。鲁甸地震引发了震中附近的次生灾害如滑坡、泥石流等，也造成了村落向远离震中且未受次生灾害影响的区域搬迁。

3 结论

本文基于分形理论的随机聚集维数，对云南3次典型地震前后极震区内乡村聚落分布特征进行对比，总结了地震对乡村聚落分布演变的影响规律，得出以下结论：

(1)地震后极震区内乡村聚落数量明显增多，说明地震破坏会导致乡村居民离开原有聚居地重新选址，乡村聚落分布更为分散。鲁甸地震后聚落数增加幅度明显低于武定、丽江地震，说明2014年因房屋倒塌选址重建的现象有所缓解，这归因于2006年以来云南省对乡村民房的抗震加固措施。

(2)地震后极震区乡村聚落的分布格局发生了明显变化：总体上震后极震区内乡村聚落围绕震中的分布相对于震前变得更为离散，说明震后乡村聚落往往会向未受震灾影响或影响轻微的区域迁移，从而改变其原有的分布特征。

(3)3次地震极震区乡村聚落分布状态离散程度的变化是不同的：武定地震后乡村聚落由震前的聚集分布变成离散分布；丽江地震后极震区乡村聚落由震前围绕震中相对高度集聚的状态变成震后相对低度集聚的状态；鲁甸地震后极震区乡村聚落由震前围绕震中相对均衡分布的状态变成震后相对离散分布的状态，这与地震前极震区内乡村聚落的分布状态以及地震的强度有关。

本文结合灾害学、乡村聚落地理学进行研究，一定程度上丰富了震灾区乡村聚落的演变研究。但由于样本数量还较少，未来有待进一步增加震例进行深化研究。