跨断层扰动协调比异常提取方法与效能评估及其在云南地区的应用*

洪 敏，张 勇，王伶俐，付 虹，李利波，刘自凤

(云南省地震局，云南 昆明 650224)

0 引言

跨断层监测作为地震监测的重要手段，在中国有近半个世纪的观测历史，跨断层资料为断层活动与地震关系的研究奠定了良好的基础。目前，对于跨断层资料的分析方法有很多，有的注重断层活动状态、不同场地活动关联性的分析，如张希等(2012，2018，2020)在跨断层资料的分析研究方面做了大量工作，提出了灰色关联度、特征强度等一系列方法用于异常的识别，且部分方法对断层活动状态有较好的描述，从一定程度上能够解释断层活动与地震之间的关系(田晓等，2021)。但受场地观测流程复杂、复测困难等因素影响，云南地区的跨断层观测多以单断层的监测为主，且多数场地分布在主干断裂的某一分支断裂，难以完全跨过主干断裂，导致分析断层活动机理与地震之间的关系比较困难。例如楚雄场地观测到的是长期左旋走滑活动，与该区域断层右旋走滑的机理不一致，不能完全代表主干断裂的活动特征。另外一些学者的方法主要是基于数学方法对观测时序进行异常分离与识别(薄万举等，2001；贾鹏等，2016；张晶等，2020；李瑞莎等，2020，2016)，但异常的识别依赖于正常背景状态的明确，这些方法能够对异常进行识别，但无法从机理上给予更多的解释。

协调比的计算通过描述断层自身各分量的协调性来表征断层周边应变积累程度，避免了断层活动与板块运动之间机理解释的矛盾性，同时也能够反映出断层异常状态与区域构造活动之间的相关性，特别适合云南地区跨断层观测场地的现状。在实际使用断层协调比描述断层协调性时，存在计算起点不同、结果出现显著差异的问题，导致其在会商应用时一直存在困难。李瑞莎等(2013)提出了改进办法，在计算断层滑动量时不再采用统一起点，而采用相邻两期的观测数据差分来计算断层的活动速率，该方法较为有效地避免了因起点不同而引起的计算结果的差异问题。从计算结果的物理意义看，李瑞莎等(2013)认为该协调比结果是断层的“瞬态协调比”，可称其为短期协调比，经过检验，断层协调比结果虽然不再受计算起点影响，但是不能较好地反映断层协调比异常的累积状态。李瑞莎等(2013)使用滑动窗计算协调比的方差来反映断层一段时间内协调比的离散程度，从一定程度上兼顾了协调比异常状态的持续时间的因素。该方法对原有协调比进行了较好的改进，利用方差虽然在反映偏离离散程度方面能够在一定程度上表达协调比偏离背景的异常频度，但在反映异常偏离累积程度及幅度、异常出现同向偏离等方面仍存在欠缺。

因此，本文提出了扰动协调比的计算方法，对“瞬态协调比”的合成算法进行了改进，在继承该方法不受起点影响的特性的同时，进一步体现了协调比持续时间和幅度等信息的合成，在表达断层异常状态的持续时间方面更具优势，以期尽可能充分显示协调比异常程度，将其并应用于震情会商中，以云南地区11处跨断层资料为例，针对川滇地区M≥6.5强震合成得到了多个预测指标。

1 协调比方法的基本原理

张晶等(2011)提出了协调比方法，该方法在区分正常动态和异常变化上有显著的优势，能够较为清晰地判别断层的异常活动情况。该方法的理论基础是，无论断层处于纯走滑还是走滑兼倾滑的无障碍蠕动状态，断层3个运动分量的比值处于相对稳定的恒定值；而当断层存在显著应变积累时，断层3个运动分量出现不协调变化，导致其比值偏离背景值，从而有效地区分正常状态和异常。许多学者针对断层协调比与地震的关系开展了大量研究工作(徐东卓等，2021；李智蓉等，2020；李瑞莎等，2012；李文静，2014；张立成，薄万举，2021；周海涛等，2018；苑争一等，2018)。

计算断层协调比时，首先根据断层观测值计算断层活动的三维分量，断层活动性各分量和断层及测线之间的关系如下(薄万举等，1998)：设测线与断层夹角为α(α定义为测线顺时针转动到与断层线重合时所转过的角度)，测线伸长量为ΔL(缩短符号为负)，上盘逆时针相对下盘的扭错量为a、水平拉张量为b、垂直上升量为c、水准变化量为Δh(a>0表示左旋、b>0表示张性、c>0表示上盘上升，由上盘到下盘为往测方向)，则在二条不同的测线上，同时施测水准和基线，可唯一确定断层运动参数：

(1)

(2)

(3)

定义f1、f2、f3为断层活动协调比，用于描述断层3个分量两两之间的协调性，并认为当断层处于无障碍的蠕滑状态时，这3个分量为恒定值，可表示为：

(4)

2 存在的问题和改进方式

从机理上来看，断层“瞬态协调比”异常存在两种可能的原因：一是按照断层协调比的定义，断层上出现显著的应变积累，导致断层活动状态发生改变，从而出现协调比异常，直到地震发生后应力得到释放为止，这类异常对应变积累区附近场地影响可能更为突出，持续时间贯穿应变积累到发震的整个过程，在此过程中计算得到的瞬态协调比将可能持续反复出现异常；二是协调比基本原理是断层分量之间的比值，受周边其他强震影响，当周边其他区域强震发生前发震断层由稳态进入亚失稳状态时，可能导致区域应力出现调整，引进应力状态发生改变，而跨断层场地位于敏感带，容易受到这种应力状态调整的影响，多个场地出现准同步的异常变化(张希等，2020)，从而导致断层协调比出现异常，可认为是强震亚失稳状态前出现的区域应变场扰动导致的异常。无论是哪种原因导致的协调比异常，瞬态协调比都可能反复出现，但可能在出现时间和幅度上存在差异。因此，为了更好地表示瞬态协调比反复出现的频次和幅度，本文提出“扰动协调比”的概念，即对于任意协调比参量时间序列，将瞬态协调比归算为一定时间窗的协调比累积值。假设现有某一跨断层场地通过相邻期观测数据计算得到的协调比分量时序为fi(i=1，…，n)，对于时序中任意时间点的值fk，假设时间窗w内，fk前有m个值，计算其扰动协调比为：

(5)

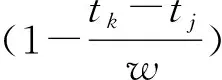
利用本文方法计算得到峨山场地年窗长的应力场扰动协调比结果(图1)。从图1可以看出，峨山场地对川滇菱形块体边界带，甚至龙门山断裂带附近的强震均有显著响应，且在强震前1～3年就已经出现，持续时间较长。因此，扰动协调比在断层状态描述方面有着显著优势，在窗长恒定时，其结果具备唯一性，与协调比计算的起点无关(图1c、d中为不同起点)。从物理意义上来说，协调比的扰动现象反映的是强震前区域应力场出现的扰动现象，这种扰动在前兆观测方面可能表现为大范围的前兆异常项数增多现象，而在断层上的观测则表现为断层活动状态偏离常态。

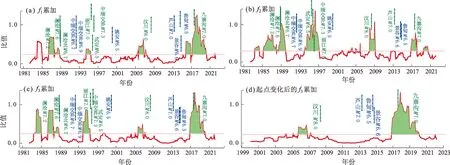
图1 峨山场地年窗长区域应力场扰动协调比时序图(绿色为准确预测地震，蓝色为漏报地震，下同)

3 扰动协调比群体异常综合指标提取方法

在进行实际分析预测时，单个场地的异常对于地震的研判往往存在依据不充分、信度不高等问题。张希等(2020)研究表明2013年芦山7.0级地震前多个断层场地出现了显著的异常变化。因此，在一次较强的地震事件前，在多个场地上应可观测到扰动协调比异常，对多个场地扰动协调比异常进行合成会更加有利于强震的判定。在合成过程中，由于不同场地所处断裂差异，对不同地震的响应也存在强弱差别。因此，可采用权重合成方式，首先对不同场地的扰动协调比进行效能评估，获取其地震对应能力，并根据评分结果对该场地出现的扰动协调比进行定权，最后合成综合预测指标。

3.1 预报效能评估

利用许绍燮提出的R值评分进行评估。统计检验中，当设定某一时间序列的异常阈值后，则超出该阈值的情况被视为异常，假设预报窗长为W，某一个异常出现的时间点位为T1，异常结束的时间点位为T2，对该异常进行预测占用的时间为T=T2-T1+W，当地震时间处于该时间段内时，视为准确预报。假设该时间序列共出现了k次异常，任意异常的时间占用为Ti(i=1，…，k)，通过对所有异常与地震事件的对应情况进行扫描，得到准确预测的地震次数为m，地震发生的总次数为n，时间序列总的时间跨度为Ttotal，则R可表示为：

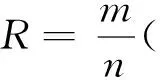
(6)

计算获得R值后，可根据预测准确数和漏报次数获得R0。如果R>R0，说明该预测指标有效。

3.2 综合异常指标合成

假设单个场地扰动协调比序列为Si(i=1，…，n)，其通过了预报效能的评估，最佳效能结果R为Ri(i=1，…，n)，R0为R0i(i=1，…，n)，则在该预测过程中，能够识别出一系列的异常时段，这些时段表征了该测项出现异常的时间点。在所有测项异常信息合成过程中，涉及到不同测项权值的确定问题。一个简单的思路是，预报效能高的测项出现异常时，给予其更高的信度，预报效能低的测项给予低的信度，预报效能高低由R来衡量。由于R可能出现负值，因此，在给定信度时，给予每个测项一个基础信度为1，对于通过预报效能检验的协调比结果，其异常给予一个较高的信度，以此为基础，可确定每个扰动协调比序列的异常信度Wi为：

Wi=[Rk+(Rk-R0k)]×exp(i=1，…，n)

(7)

式中：exp为放大因子(本文中取值为10)，用于增加效能评估结果优秀的场地的信度，信度的定义避免了R<0的情况，同时，兼顾了R偏离R0的程度，充分体现了指标的信度。扫描每个时间序列，将其出现异常的时段赋值为Wi，其他正常时段赋值为0，则可得到新的时间序列S′i(i=1，…，n)，该时间序列反映了不同时段发生地震可能性的强度，通过对多个时间序列的信度进行集成，可获得最终的协调比异常信度合成时序S总为：

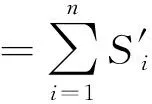
(8)

并进一步对该合成时序进行预报效能评估，获得预测指标。

4 案例分析

4.1 基础数据及地震目录的选取

本文案例分析主要选取云南地区11个跨断层场地数据(图2)。由于扰动协调比主要反映强震前应力场状态的调整，因此，主要选取1981—2021年云南地区(97°～106°E，20°～29°N)M≥6.5地震以及川滇地区(97°～106°E，20°～34°N)的M≥7.0地震，见表1、图2。

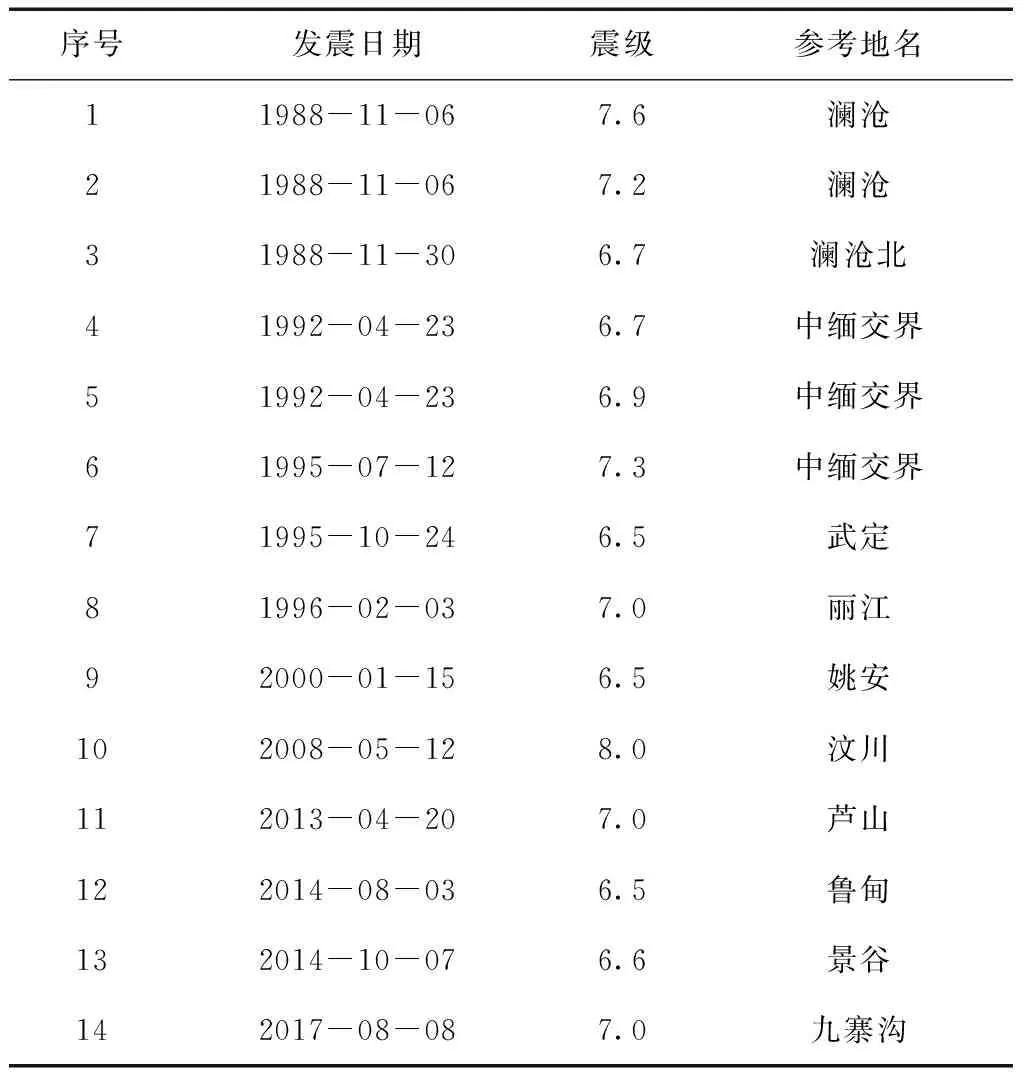
表1 本文研究选取的1981—2021年川滇地区M≥6.5地震

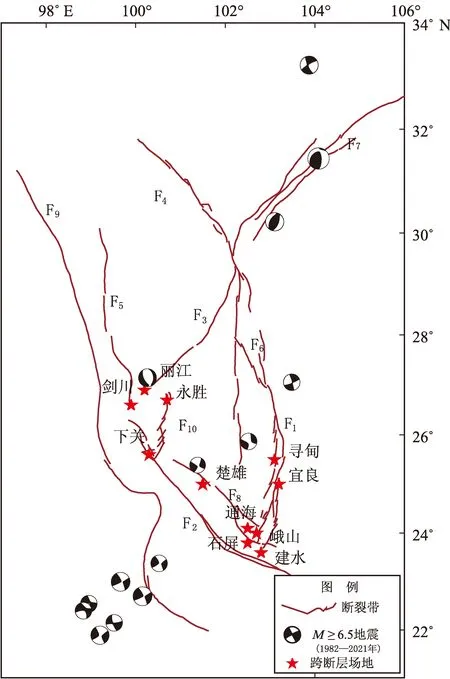
F1：小江断裂；F2：红河断裂；F3：丽江—小金河断裂；F4：鲜水河断裂；F5：金沙江断裂：F6：安宁河—则木河断裂；F7：龙门山断裂；F8：楚雄—建水—石屏断裂；F9：澜沧江断裂；F10：程海断裂

4.2 单场地扰动协调比效能评估结果

计算云南地区11个场地的扰动协调比分量，并根据表1中选取的地震进行效能评估，33个扰动协调比分量中，通过效能评估的共12项(R≥R0的测项)，见表2、3。

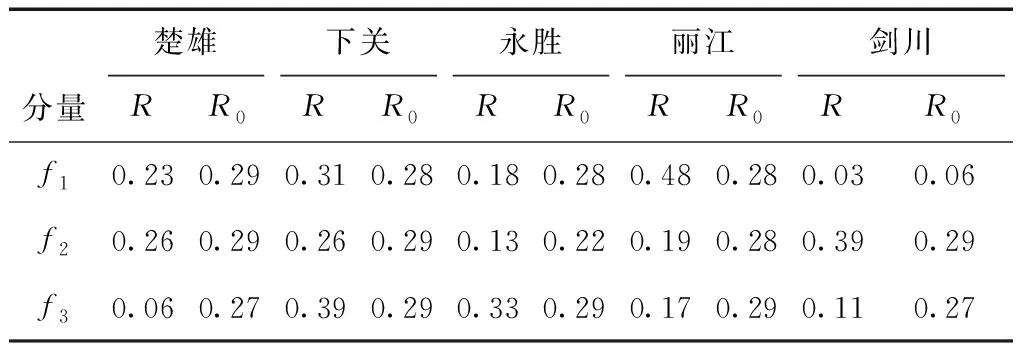
表2 滇西单场地协调比效能评估结果

表3 滇南单场地协调比效能评估结果

4.3 扰动协调比综合预测指标的提取

扰动协调比综合指标的提取需要对多个场地协调比信息进行合成，合成过程有多种策略可选，可以对扰动协调比进行等信度合成，最大限度保留所有分量的异常信息，但由于不同协调比分量对地震样本的敏感性差异，可能导致合成结果在进行效能评估时无法取得较好的效果。因此，本文基于R评估结果对不同分量进行定权，进而完成信息合成，可显著提升综合指标的预报效能。为了对比不同合成策略的预测效果，本文选择4种合成策略进行对比，结果见表4。

表4 扰动协调比综合指标合成策略预测效果

从表4可以看出，总体上，非等信度合成结果明显优于等信度合成结果。从33个分量合成结果(图3)可见，整个合成曲线的异常形态基本相似，但等信度合成结果存在较多的漏报地震现象。具体来看，1996年丽江7.0级、2014年鲁甸6.5级、2014年景谷6.6级以及2011年缅甸7.2级(未纳入地震样本)地震前，协调比异常均在震前出现了趋势上升的现象。但和历史对比看，没有达到预报阈值，所以导致了漏报。但总体来说，震前出现协调比群体异常显著上升的现象还是比较明显的。

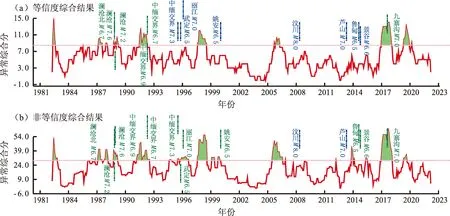
图3 全部协调比分量合成结果

通过效能评估的12个协调比分量可能在地震信息的响应方面有较为显著的优势(图4)。因此，对12个优选扰动协调比分量的信息进行合成，发现其R评分结果具有较为显著的优势，地震对应效果有显著的提升。从等信度和非等信度合成结果看(图4)，地震报准次数并无显著差异，非等信度方式报准地震增加了2013年芦山7.0级地震，且非等信度信息合成指标的预测时间占有率和虚报次数都有一定下降，所以非等信度合成结果相对更优。

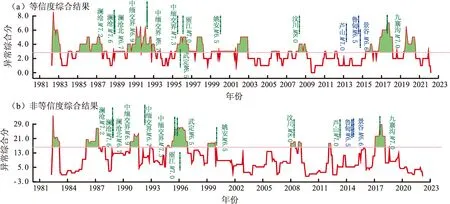
图4 12个协调比分量合成结果

5 结论与讨论

本文在瞬态协调比合成算法的基础上提出扰动协调比计算方法，以云南地区11处跨断层资料为例，针对1981—2021年川滇地区6.5级以上强震样本开展了震例总结和综合预测指标的提取，对预测指标进行效能评估，得到以下结论：

(1)扰动协调比计算方法在跨断层场地异常活动状态的提取中有一定优势，与周边强震存在较好的相关性，说明震前由于区域应力场的变化，导致断层的活动出现背离背景的现象，利用该现象开展强震的预测具有一定的意义，能够较好地识别震前断层出现的协调比异常状态，对于强震可能发生时间可提供中期尺度的判定依据。

(2)扰动协调比计算方法在异常信息的累积方面做出了进一步的优化，从而有效体现了一定时间尺度内断层的异常活动状态的持续效应，提升了异常信息的信噪比，有利于后续的震例总结，在震前异常的提取方面有较好优势。

但从目前计算的结果看，扰动协调比仍然存在震后效应和震前异常无法完全区分的问题。如2005年以后各个合成指标均出现不同程度的异常，特别在全部扰动协调比分量合成结果中更加明显，而该异常从大区域的地震活动看，可能与2004年印尼9.3级地震震后影响有关。因此，在扰动协调比信息合成过程中，地震样本的选取尤为重要，从扰动协调比的基本原理来说，应当和一些震级较大的地震相关性更好，因为此类地震造成的区域应变场的扰动范围可能更大，群体异常出现的几率更高。

本文研究中地震的选取不一定合理，但在一定程度上说明了在强震前由于区域应力场的扰动，存在导致跨断层场地断层协调比背离正常背景的现象，这种现象持续时间1～3 a不等，通过扰动协调比的计算方法能够较好地提取到这些异常现象。通过进一步震例的总结和筛选，可提取出符合本区域的扰动协调比综合预测指标，辅助会商决策。