Characterizations of Cycle-Forced 2-Connected Claw-Free Cubic Graphs

(School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China)

Abstract: Let G be a graph and C be an arbitrary even cycle of G.The graph G is called a cycle-forced graph if G-V(C) has a unique perfect matching.When C is an arbitrary induced even cycle of G, G is called an induced-cycle-forced graph.If G-V(C)has no perfect matching, G is said to be cycle-bad.This paper gives characterizations of these three type of graphs in the class of 2-connected claw-free cubic graphs.

Keywords: Perfect matching;Cubic graph;Claw-free graph;Cycle-forced graph

§1.Introduction

Every graph considered in this paper has no loop,but it may have parallel edges.We follow the notations and terminology in [1].LetGbe a graph with vertex setV(G) and edge setE(G).A subsetMofE(G) is called aperfect matchingofGif no two edges inMare adjacent,andMcovers all vertices ofG.Theperfect-matching polytopeof a graphGis the convex hull of the incidence vectors of all perfect matchings ofG.Chv´atal [5] showed that two vertices of the perfect matching polytope are adjacent if and only if the symmetric difference of the two perfect matchings is a cycle.This result leads to the definition of the perfect matching graph ofG.Theperfect matching graphofG,denoted byPM(G),is the graph whose vertices are the perfect matchings inG,with two verticesM1andM2adjacent inPM(G) if the symmetric difference ofM1andM2is a cycle.A graphGisperfect matching compact[8],orPM-compactfor short,if the graphPM(G) is complete.For the results of PM-compact graphs,see [8–10].

The definition of PM-compact graph implies that for a graphGhaving perfect matchings,Gis PM-compact if and only if for each even cycleCofG,G-V(C) has at most one perfect matching.A cycleCof a graphGis called aforced cycleifG-V(C) has a unique perfect matching.In [3],Che and Chen proposed the concept of forcing face in a plane bipartite graph,which is a natural generalization of the concept of forcing hexagon of a hexagonal system introduced by Che and Chen [2].For a connected plane bipartite graphGwith the minimum vertex degree at least 2,a facefofGis said to be aforcing faceifG-V(f) has exactly one perfect matching.Therefore,the concept of forced cycle is a generalization of forcing face.For the results on forcing faces,see [3,4].A graphGis called acycle-forced graph(CF-graphfor short) if each even cycle inGis a forced cycle.If for each even cycleCofG,G-V(C) has no perfect matching,Gis called acycle-bad graph(CB-graphfor short).Clearly,both CF-graph and CB-graph are PM-compact.In [11],there is a characterization of cycle-forced hamiltonian bipartite graphs.

A subgraphHof a graphGis anice graphifG-V(H) has a perfect matching.A graph is called ainduced-cycle-nice graph[7] (ICN-graphfor short) if its each induced even cycle is a nice cycle.A graph is called ainduced-cycle-forced graph(ICF-graphfor short) if its each induced even cycle is a forced cycle.A graph isclaw-freeif it has noK1,3as induced subgraph.In fact,a CF-graph is an ICF-graph,and an ICF-graph is an ICN-graph.Peng,Wang,and Zhou [7]characterized 2-connected claw-free cubic ICN-graphs.

This paper gives characterizations of 2-connected claw-free cubic ICF-graphs,CF-graphs and CB-graphs.

§2.Preliminaries

Lemma 2.1.([6]) Every connected claw-free graph with even number of vertices contains a perfect matching.

LetGbe a graph.Ak-vertexofGis a vertex with degreek.We useL(G) to denote the set of 1-vertices ofG.AtriangleofGis a cycle on three vertices.Replacing a 3-vertexvofGby a triangle is to removevfromG,and add a triangle on three verticesv1,v2,v3so that the three edgese1,e2,e3which are incident withvinGare incident withv1,v2,v3respectively.

A graph is called adiamondif it isK4-e,whereeis an edge ofK4.A string of diamondsis a graph constructed from diamondsD1,D2,...,Dkin the following way: for each1,2,...,k-1},a 2-vertex ofDiis adjacent to a 2-vertex ofDi+1so that the resulting graph has exactly two 2-vertices and all other vertices are 3-vertices.Whenk1,a string of diamonds is,in fact,a diamond.The graph obtained from a string ofkdiamondsS,k ≥2,by adding an edge which connects the two 2-vertices ofSis calleda ring of diamonds.The string ofkdiamonds or the ring ofkdiamonds isoddorevenaccording to the parity ofk.

By a diamond ofGor a string of diamonds ofG,we mean a subgraph ofGwhich is isomorphic to a diamond or a string of diamonds,respectively.For convenience,when we say a string of diamonds ofG,we mean a maximal string of diamonds ofGwith respect to inclusion.Since each vertex ofGis a 3-vertex,inGno two distinct strings of diamonds have a vertex in common.

To replace an edgeeuvofGby a string of diamondsSeof whichxandyare two 2-vertices is to removeefromGand add edgesuxandvyto connectSe.Then for each diamondDinSe,deleting a 3-vertex ofD,we obtain auv-path.We call this path adiamond path.A diamond path is odd or even according to the parity of the number of diamonds inSe.The length of an odd diamond path is even,and the length of an even diamond path is odd.

LetH1,H2,...,Hkbek2-connected cubic multigraphs,leteiuivibe an edge ofHi,1≤i≤k,andHbe the graph obtained from the union ofH1-e1,H2-e2,...,Hk-ekby addingknew edgesfiviui+1,1≤i≤k-1,andfku1vk.The graphHis calleda ring of multiblocksand the new edgesfiare calledsupporting edgesofH.Whenk1,H1has only one supporting edgef1,which may be an arbitrary edge ofH1.Note,also,that a ring of diamonds is a ring of multiblocks,and a ring of multiblocks is a 2-connected cubic multigraph.

For a 2-connected cubic multigraphH,letH△denote the graph obtained fromHby replacing each vertex ofHby a triangle.ThenH△is a 2-connected cubic simple graph.Each triangle ofH△is a triangle which is obtained by replacing some vertex ofH,and so any two triangles ofH△are disjoint.Furthermore,H△contains no diamond.For convenience,we sayE(H)⊂E(H△).ThenE(H) is a perfect matching ofH△.WriteH△{H△:His a 2-connected cubic multigraph}.

Lemma 2.2.([7]) Suppose that H is a 2-connected cubic multigraph,and C is a cycle of H△of length at least four.Then C is an induced even cycle of H△if and only if the edges of C lie alternately in E(H)and triangles of H△.

LetHdenote the set of graphs each of which is built from a 2-connected cubic multigraphHby replacing some edges ofHby strings of diamonds,and replacing each vertex ofHby a triangle.Thenis a subset ofH.

Lemma 2.4.([7]) Suppose that GH and G is an ICN-graph.If C is an induced even cycle of G,then C contains no diamond path.

Lemma 2.5.([9])Let G be a claw-free cubic matching-covered graph.Then G is PM-compact ifand only if G is (the cubic graph with two vertices),K4or H△4,K3,3}.

§3.Main results

In this paper,we obtained the following three results on 2-connected claw-free cubic graphs which have no parallel edges.

Theorem 3.1.Let G be a 2-connected claw-free cubic graph.Then G is an ICF-graph if and only if either

(i) G is K4;

(ii) G is an odd ring of diamonds;

(iii) G is H△,or G is built from H△by replacing an arbitrary edge of H by an odd ring of diamonds,where H {,K4,K3,3}.

Theorem 3.2.Let G be a 2-connected claw-free cubic graph.Then G is a CF-graph if andonly if G is K4or G is

From Lemma 2.5,Theorem 3.2,and the fact that a 2-connected cubic graph is matching covered.we have the following result.

Corollary 3.1.Let G be a 2-connected claw-free cubic graph.Then G is a cycle-bad graph if and only if G is H△4,K3,3}.

In Section 4,we prove Theorem 3.1,which gives a characterization of 2-connected claw-free cubic ICF-graphs;and in Section 5,we prove Theorem 3.2,which gives a characterization of 2-connected claw-free cubic CF-graphs.

§4.Proof of Theorem 3.1

Lemma 4.1.Suppose that G is K4or an odd ring of diamonds.Then G is an ICF-graph.

Proof.SinceK4has no induced even cycle,K4is an ICF-graph.Suppose thatGis an odd ring of diamonds.LetE′be the set of all edges ofGwhich connect distinct diamonds ofG.IfCis an induced even cycle ofG,thenE′⊆E(C),and for each diamondDinG,Ccontains two edges ofD.NowCis an odd cycle,a contradiction.So an odd ring of diamonds has no induced even cycle.ThusGis an ICF-graph.

A graphGis ak-caterpillarif deleting all 1-vertices fromGthe resulting graph is a path withkvertices.For convenience,we sayK2is a 0-caterpillar.An edgeeofGis called anpendent edgeif one end ofeis a 1-vertex.For a cycleC,a pathPis call abridgeofCif its two ends lie inCbut its internal vertices do not lie inC.Two bridgesBandB′areskewif the two endsu,vofB,and the two endsu′,v′ofB′occur in the cyclic orderu,u′,v,v′onC.

Fig.1 K4

Fig.2 K3,3

Conversely,suppose that4,K3,3}and{e}.ThenGis built fromH△by replacing the edgeeby an odd string of diamondsSe.Letuandvbe the two ends ofe,and letxandybe the two 2-vertices ofSe.Suppose thatux,(G).LetCbe an induced even cycle ofG.IfCcontains a diamond path,thenC-V(Se) is a path inH△whose edges lie alternately inE(H) and triangles ofH△and whose two end edges lie in triangles ofH△.SoC-V(Se) is a path of odd length.Recall that the length of an odd diamond path is even.ThusCis an odd cycle,a contradiction.ThereforeCis an induced even cycle ofG-V(Se),also an induced even cycle ofH△-e.By Lemma 2.2,the edges ofClie alternately ofH-eand the triangles ofH△.By Lemma 4.4,H△is an ICF-graph.SoE(H)E(C) is the unique perfect matching ofH△-V(C).Obviously,(H)E(C).Note thatG-V(C) can be obtained fromH△-V(C)by replacing the edgeebySe.LetMbe the union of(E(H)E(C){e})∪{ux,vy}and a perfect matching ofSe-x-y.SinceSeis an odd string of diamonds,Se-x-yhas a unique perfect matching.Consequently,Mis the unique perfect matching ofG-V(C).ThusGis an ICF-graph.

From Lemma 2.3,Lemma 4.4 and Lemma 4.5,we complete the proof of Theorem 3.1.

§5.Proof of Theorem 3.2

Lemma 5.1.Both K4andC6are CF-graphs.

Proof.Since all even cycles ofK4are 4-cycles,K4is a CF-graph.LetCbe an even cycle ofThenCis either a 4-cycle or a 6-cycle.For the former case,G-V(C) is an edge;For the latter case,G-V(C) is null.ThusGis a CF-graph.

Lemma 5.2.If G is an odd ring of diamonds,then G is not a CF-graph.

Proof.Suppose thatGhaskdiamonds,thenkis odd andk ≥3.LetE′be the set of all edges ofGwhich connect distinct diamonds ofG,then|E′|k.LetCbe a cycle ofGsatisfying the conditions:E′⊆E(C),for one diamondDinG,Ccontains three edges ofD,and for each otherk-1 diamonds inG,Ccontains two adjacent edges.Then|E(C)|k+3+2(k-1)3k+1.Sincekis odd,|E(C)|is even,that is,Cis an even cycle ofG.Note thatG-V(C) is the union of isolated vertices.SoG-V(C) has no perfect matching.This impliesGis not a CF-graph.

Lemma 5.3.4,K3,3},then H△is not a CF-graph.

Proof.EitherHK4orHK3,3,H△has a cycleCof length|V(H△)|-2 such thatH△-V(C) is the union of two isolated vertices.SoH△-V(C) has no perfect matching.ThenH△is not a CF-graph.

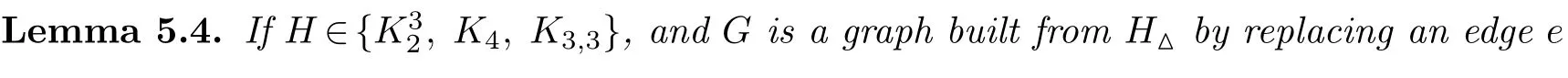
Since a CF-graph is an ICF-graph,from Theorem 3.1,Lemmas 4.6-4.9,we complete the proof of Theorem 3.2.

Acknowledgments

Wang Xiumei is Mr.Lin Yixun’s master student (2000) and doctoral student (2004).This article is to celebrate Mr.Lin’s 85th birthday.