AC-HAPE3D：基于强化学习的异形填充算法

朱鹏辉，袁宏涛，聂勇伟，李桂清

AC-HAPE3D：基于强化学习的异形填充算法

朱鹏辉，袁宏涛，聂勇伟，李桂清

(华南理工大学计算机科学与工程学院，广东 广州 510006)

在3D打印、快递物流等领域，需要将形状各异的零件或货物在限定的空间中摆放，称为异形填充。给出一种摆放方案，以便将尽可能多的多面体放入给定容器；或者一批物体紧密地摆放，使得占用体积最小，则称为异形填充问题。这是个NP问题，很难高效求解。基于此，研究在一个可变维度的三维容器内摆放给定的一组多面体，使得打包后容器的可变维度最小。并提出一个基于强化学习的算法AC-HAPE3D，利用启发式算法HAPE3D将问题建模为马尔可夫过程，再利用基于策略的强化学习方法Actor-Critic进行学习。同时用体素来表示容器和多面体，从而简化状态信息的表达，并用神经网络表示价值函数和策略函；为了解决状态信息长度以及动作空间可变的问题，采取遮罩的方法来屏蔽部分输入和输出，并且引入LSTM来处理变长的状态信息。在5个不同的数据集进行的实验表明算法能够取得较好的结果。

异形填充；启发式算法；体素；强化学习；三维打印

三维集装优化问题作为一个经典的组合优化问题，已经有了很长时间研究历史和广泛的应用场景。早期的研究关注解决交通运输中货物运载的优化，其目标要么是在长方体形状的货箱中装入尽可能多的货物，要么是固定长方体中装入尽可能高价值的货物，这样的问题称为三维集装优化问题(3D bin packing problem，3D-BPP)[1]。MARTELLO等[1]对这个问题进行了细致的研究，断定其是一个多项式复杂程度的非确定性(non-deterministic polynomial，NP)问题，并给出了其下界和精确求解算法。此外，也有一些工作[2-4]用启发式算法来求得近似解。

当货物的形状不再是长方体，而是任意的几何形状时，问题就成了三维异形填充(3D irregular packing，3DIP)。其应用场景更为复杂，还经常伴随有额外约束。如，在3D打印中需要将要打印的零件在工作台上进行布局，由于3D打印按层构建的方式，对于零件之间的距离、堆叠都有限制，；在电商行业中，将商品装入快递箱中也需要考虑到货物密度以及用缓冲物填充空隙，这些问题均可以描述为3DIP。

3DIP问题根据优化的目标和约束条件分为不同种类。ARAÚJO等[5]依照问题的维度(dimensionality，D)、优化目标(criteria，C)、容器类型(build，B)和问题特性(attributes，A)进行分类。基于此，本文所研究的问题类型为3/Si/Oo/A，即三维，单容器一个维度大小可变，目标是使得可变维度的大小最小，无额外约束，具体描述如下：

此类型的3DIP问题出现在基于选择性激光烧结(selective laser sintering，SLS)的3D打印技术中。在这种情况下，容器的高度一般不是无限的但是足够长，可以视为可变的维度，同时对于打印部件没有诸如支撑结构之类的要求，自由度很高，此时最小化高度即为最小化材料的消耗，因此存在3DIP问题。

1 相关工作

3DIP问题最终归结为组合优化问题，组合优化问题常见的解法在对3DIP的研究中也都有出现，如启发式算法、设计数学模型等等，也有专门的异形填充算法，如临界多边形(no-fit polygon，NFP)方法。

很多早期的研究采用的是启发式算法，如采用遗传算法和模拟退火算法[6-7]。文献[6]为SLS设计了一个基于遗传算法的方法，即在“染色体”上编码了打印部件的顺序和朝向，依据上述信息尝试放置部件，再通过遗传算法来搜索更优的结果。LIU等[8]提出了基于最小化势能的启发式算法(heuristic algorithm based on the principle of minimum total potential energy，HAPE3D)，首先在容器中均匀地放置打包点，并按一定顺序为每个多面体找出势能最小的位置。WANG和HAUSER[9]为机器人自动装货提供了一个高度图最小化(heightmap minimization，HM)启发式算法，考虑了货物放置时的稳定性和可操作性，为每个候选的变换计算货箱内的高度图，再用变换和高度图计算分数，算法结果倾向于稳定，且可操作性强。WU等[10]按照可变尺寸的三维不规则容器、可变尺寸的三维长方体容器和单个容器，将3DIP分解为3个问题，建立了每个子问题的数学模型，并提出了三阶段启发式算法，在真实的随机实例上验证了算法的有效性。

通过数学模型来解决3DIP的方法，最早在文献[11]中提出。其通过将凹多面体分解为凸多面体表示，在其提出的Phi函数的基础上，构造出了3DIP的数学模型，并提供了一个能找到全局最优解的方法，但该方法需要将凹多面体提前分解为凸多面体，不支持旋转，同时计算耗时大，因此其通过提供一些预定义的凸多面体，将凹多面体近似地分解为这些凸多面体，提供了一个找到近似解的方法。WOLCZYK[12]使用深度学习实现了基于Phi函数的局部解算器，自动梯度计算可以与GPU并行计算，从而加速计算。STOYAN等[13]提出了新的Quasi-Phi函数，为打包椭圆提供了新的数学模型。ROMANOVA等[14]在Quasi-Phi函数的方法上进行了扩展，将其从只能处理椭圆扩展到了能处理任意凹多面体上，把3DIP问题建模为了非线性优化问题，并通过非线性优化求解器直接求解，且支持任意的移动和旋转。但该算法仍然需要将多面体分解为凸多面体才能计算，且很难加入新的约束，应用范围有限。

临界多边形(no-fit polygon，NFP)最早在文献[15]中提出，用于解决二维的异形填充问题。NFP可描述出一个多边形相较于另一个多边形，在空间中放置的区域，但由于计算开销大且计算难度高，在3DIP中的应用较少。为了降低NFP的计算开销和难度，VERKHOTUROV等[16]提出计算基于体素的NFP，之后在选择多面体的放置位置时，也将容器划分为体素，再深度优先地搜索可用的位置。该算法最终在打包高度和耗时上表现的都较差。LAMAS-FERNANDEZ等[17]提出了临界体素(no-fit voxel，NFV)的概念，基于NFV的离散表示提出了一种构造性算法和一种迭代局部搜索，以及2种在包含重叠的解空间上搜索的元启发式技术，有效地解决了3D打印行业中的复杂几何体的真实实例，证明了使用不同精度的体素表示更适合现实问题。

在3DIP中，近期的研究并没有基于强化学习的。但在3D-BPP中，已经有了一些研究，VERMA等[18]提出基于强化学习的PackMan算法，用于解决在线的3D-BPP——货物并未预先给出，而是每次给出一个，该算法为当前状态计算出潜在位置作为动作，用DQN方法来学习策略-价值函数进行决策，其结果相较于一些经典方法有显著的提升。ZHANG等[19]提出了Attend2Pack方法，用于离线的2D-BPP和3D-BPP，并将动作空间分解为了选择货物和决定货物的位置和朝向，用多代理强化学习来解决，其结果相较于同期方法有着显著的优势。可以看到强化学习在3D-BPP中已经有运用且得到了较好的结果，而本文探索了强化学习在3DIP上的应用方法。

上述算法中，启发式算法和设计数学模型的方法都可以得到较好的结果，但同时计算时间长，从几十分钟到几十小时不等。而基于NFP的方法并不能得到好的结果。基于强化学习的方法在3D-BPP中得到了较好的结果，尚无在3DIP中的尝试。

2 HAPE3D算法和Actor-Critic方法

2.1 基于最小化势能的启发式算法

基于最小化势能的启发式算法(heuristic algorithm based on the principle of minimum total potential energy，HAPE3D)[8]基于最小化势能的原则，按一定顺序将多边形装入容器中。由于其计算流程简单直接，效果也比较好，而且可以支持任意形状多边形以及有限数量的旋转，因此选择该算法作为本文强化学习算法的基础，同时给出在算法实现上做出的优化。

2.1.1 算法流程

本文给出的HAPE3D算法步骤如下：

步骤1. 将所有多面体按照体积降序排序，并依次将多面体打包入容器中；

步骤2. 在容器中，按照给定的间隔，在水平和竖直方向上，均匀地放置打包点，将这个间隔称为打包间距(packing point distance，PPD)，打包点的总数量设为打包数(packing point number，PPN)；

步骤3. 将当前多面体，依次放到各个打包点上，用基于阈值的射线相交算法 (threshold-based ray-crossing algorithm，TBRC)检查是否放在了可行的打包点上；

步骤4. 在可行的打包点，即未在相交的点上，计算对应的重心高度，其重心高度最小的就是最优的点，可将这个多面体就放置在这个点上；

步骤5. 因为打包点是离散的分布在容器内，会导致多面体之间以及多面体和容器之间产生间隙，本文提出了一种间隙消除算法，来最后确定多面体的位置；

步骤6. 处理完所有多面体，算法结束。

2.1.2 实现优化

HAPE3D算法的主要计算瓶颈在于寻找可行点，即需要进行大量的多面体分离测试，因此可以通过减少分离测试次数进行加速。先进行包围盒相交测试，在确定相交时进行进一步测试。在容器内已有大量多面体时，可以快速地过滤掉大部分不相交的多面体。

HAPE3D算法还能够支持并行优化。在为每个不同旋转的多面体确定打包点的时候，可以将每个旋转所对应的流程进行并行计算，将每个计算的结果保存在数组中，待所有计算都结束后，再从中选出重心最低的作为结果。

2.2 Actor-Critic方法简介

强化学习的一个经典方法是Actor-Critic方法[20]，其是基于策略的方法，直接学习每个动作的概率，依据概率选择动作。

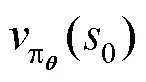
SUTTON和BARTO[21]证明了策略梯度定理，因此可以通过梯度上升的方法来求得最大值。在Actor-Critic方法中，利用价值函数来指导策略函数的参数更新，即设一个可微分的参数化价值函数为

更新参数和为

其中，和为学习率。

3 AC-HAPE3D基于强化学习的异形填充

3.1 问题建模

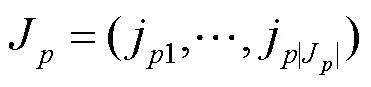
3.1.1 状态空间

在给定了容器和多面体的情况下，状态可以用J和J来唯一确定，但仅靠索引来描述状态无法全面刻画出多面体在容器中占位的实际分布，也无法表示剩余的多面体的几何特征，在用Actor-Critic方法学习价值函数和策略函数时，难以训练出有较强泛化能力的模型。因此实际具体应用时，除了J与J，还引入了如下信息: 容器体素网格，容器参数，未打包多面体的体素网格和体积。容器体素网格通过体素化容器内已经打包的多面体获得，记为V。当前所有多面体顶点坐标中最大值记为高度h，容器的长宽固定为和，已打包多面体的总体积记为V，则容器参数为C={,,h,V}。

3.1.2 动作空间

动作是指选择下一个要打包的多面体，随后选定的多面体将通过HAPE3D算法得到对应的位置和旋转，并被移入到已打包的序列中。在当前状态下，可以采取的动作由未打包的多面体决定，动作和未打包的多面体索引是一一对应的，即动作空间为={1,2,···,a}，每个动作就表示选择了对应索引的多面体。

3.1.3 奖励设计

在3DIP中，最终目标是使得打包的高度最小，即使得终止状态下的高度h最小。设每个时间步状态对应的高度为h，+1时刻状态的高度相对于上一次高度的变化量为Δh+1=h+1-h，该变化量的相反数就作为本次动作所带来的奖励，即R=-Δh。显然，在该奖励函数下最大化回报，就等同于最小化高度。

3.2 基于Actor-Critic强化学习模型的异形填充算法AC-HAPE3D

本文选择Actor-Critic[20]方法作为强化学习框架，考虑到状态信息的复杂性，采用神经网络的形式来表示策略函数和价值函数。同时限定多面体数量最多为50，那么输入的多面体体素网格和体积数量也最多为50，而当环境中的多面体数量不足50个或某些索引的多面体已经被打包时，可用0将其填充到50个，并用一个布尔值数组来表示非填充值，该数组称为遮罩数组。

3.2.1 神经网络结构设计

神经网络的架构如图1所示，可以分为输入层、隐藏层和输出层：①输入层为当前状态中所包含的信息，分为5个，在图中按序号a)～e)标出，其中a)～d)为对应状态信息的输入，而e)是遮罩输入； ②隐藏层对不同的信息用不同的节点进行特征提取，之后拼接在一起用一个全连接层进行处理并连接到输出层，其中对体素网格进行特征提取的部分参考了文献[22]，其用三维卷积完成体素网格的分类任务，本文用作特征提取；③输出层通过全连接层输出价值和输出各个动作概率，在图中用I)和II)标出，考虑到策略函数和价值函数都接受同样的输入，因此可共用同样的特征提取网络，即接受相同隐藏层的特征提取结果，再分别通过一个全连接层来获得不同的输出。

图1 神经网络结构

输入接受50个多面体体素网格，但依据遮罩信息，其中存在不需要参与运算的部分，因此用一个长短期记忆(long short-term memory，LSTM)层[21]来处理。LSTM层是循环计算的，其输入是一个二维张量，第一维称为时间步，第二维是特征值。可在时间步上循环计算，每次将当前时间步的特征值以及上一时间步的输出进行特定的运算，得到当前时间步的输出，将最后一个时间步输出的一部分作为LSTM层的输出。在循环中，如果对应的遮罩值为假，则直接将上一时间步的输出作为这一时间步的输出，达到跳过这一时间步的效果。这样可通过LSTM层和遮罩信息处理状态信息中变长的部分。

3.2.2 损失函数设计

用神经网络来拟合价值函数和策略函数，需要分别对这2个函数计算损失。

价值函数的损失采用Huber损失函数[23]进行计算，即

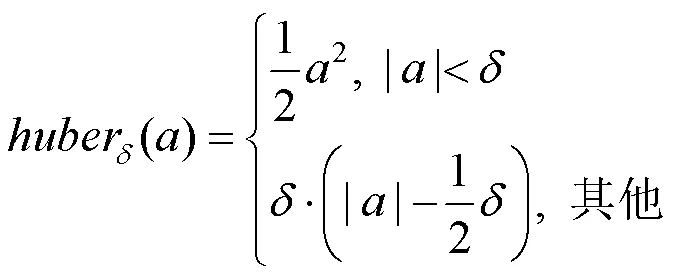
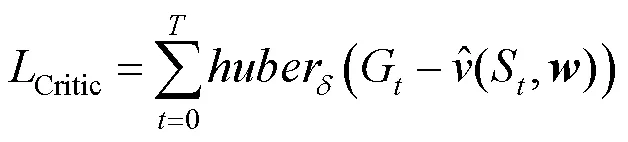
为每个时间步的价值计算Huber损失，求和作为价值函数的损失。

策略函数的损失按照Actor-Critic方法的更新方式为

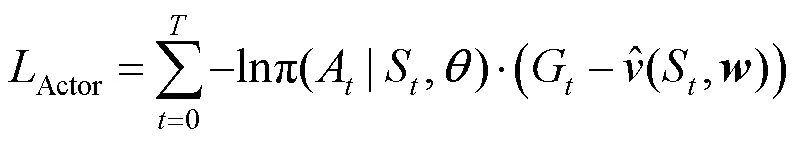
策略函数返回的是选择动作的概率，使用log函数会使得损失对小概率的动作更加敏感，对每个时间步所采取的动作计算损失，求和作为策略函数的损失。

神经网络的损失则为上述2个损失之和，即

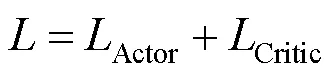
4 实验与分析

网络训练在CPU为i7-6700K、GPU为GTX1080以及内存16 GB的设备上进行。使用文献[8]中的数据集，即下文中的L2015，作为训练集，容器的长宽均为20，为了减少训练所需的时间，每个多面体的个数减少到原本的四分之一，本文使用Adam优化器，学习率设为0.001，以此进行训练。在训练了660个回合后，得到的打包结果高度为10.6，作为参考HAPE3D算法在训练集上得到的结果为11。后面将用AC-HAPE3D代表本文方法。

此外，通过移除模型中的策略函数输出的Softmax层以及价值函数，可将模型输出转换为直接输出每个行动的价值，且贪心地选择预测价值最高的行动，记为A-HAPE3D模型。此时损失简单地用Huber函数计算真实值和预测值的偏差。在同样的训练集和优化器下，训练1 000个回合后得到结果为11.4。

4.1 异形填充实验

实验在L2015，S2004，A2018和一个只有球形的数据集Spheres以及M2000的5个数据集上分别进行。L2015[8]由5种多面体组成，容器的长宽均是20，共1个测试，其包含36个多面体；S2004[11]由10种多面体组成，容器的长和宽分别为35和30，共5个测试，依次包含20，30，40和50个多面体，每个测试中各种多面体的数量均相同；A2018[5]包含了大量不同的用于3D打印的零件模型，选择其中9个不同的零件进行打包，容器的长宽分别为285和155；球形数据集Spheres由39个半径为1，10个半径为2和一个半径为5的经纬球模型组成，容器的长和宽均是12；M2000[1]是为3D-BPP设计的测试，模型均为长方体，并选择了其中Class 9的3个测试，分别由10，20和30个长方体组成，容器长宽均是10，最优解高度均为30，此时容器被完全填充。

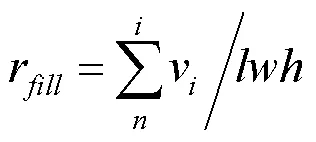
第1个实验在数据集L2015上进行，包含1个测试，打包结果如图2所示，与其他算法的比较见表1。

图2 L2015打包结果

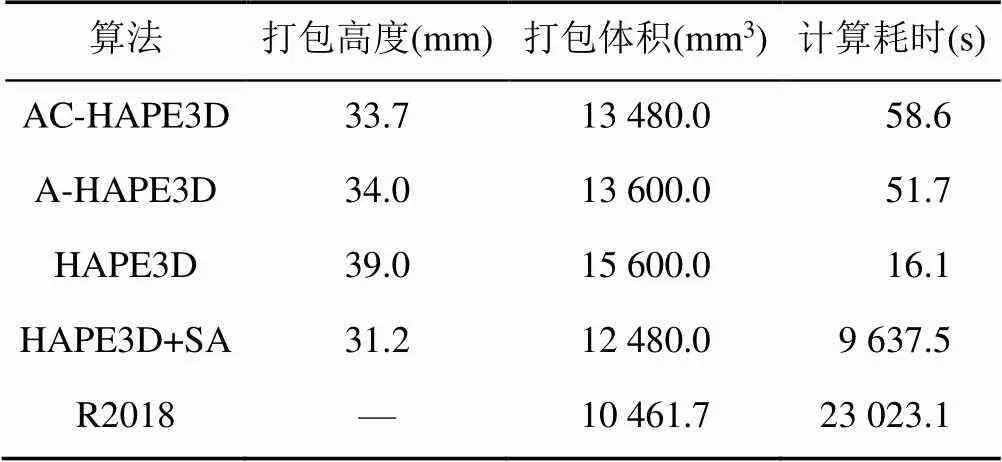
表1 L2015结果比较

第2个实验在数据集S2004上进行，包含4个测试，打包结果如图3所示，与其他算法的比较见表2～表4。

第3个实验A2018和第4个实验Spheres的实验结果如图4所示。

第5个实验M2000的实验结果如图5所示。

实验3，4，5的打包耗时、高度和填充率见表5。

4.2 实验结果分析

首先分析数据集L2015和S2004上的实验数据。

从表1和表2可以看出，本文算法在打包高度上显著优于HAPE3D算法，而且随着多面体数量增加，优势也变得更大；综合表1和表4则表明可知，本文算法要比HAPE3D更耗时。

图3 S2004打包结果((a)测试1～20个多面体；(b)测试2～30个多面体；(c)测试3～40个多面体；(d)测试4～50个多面体)

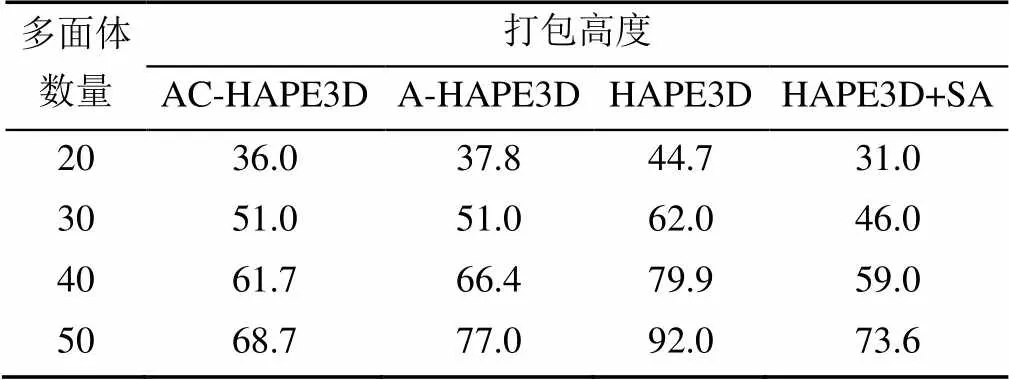
表2 S2004结果高度比较(mm)

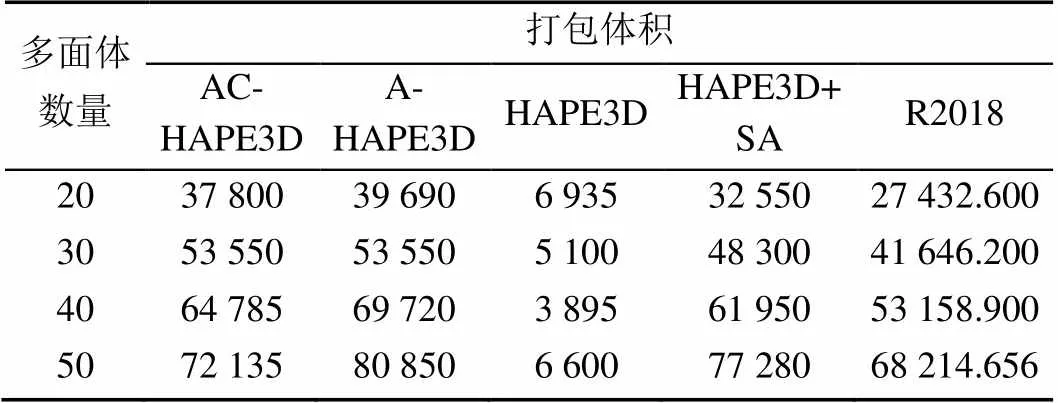
表3 S2004结果体积比较(mm3)

表4 S2004结果耗时比较(s)

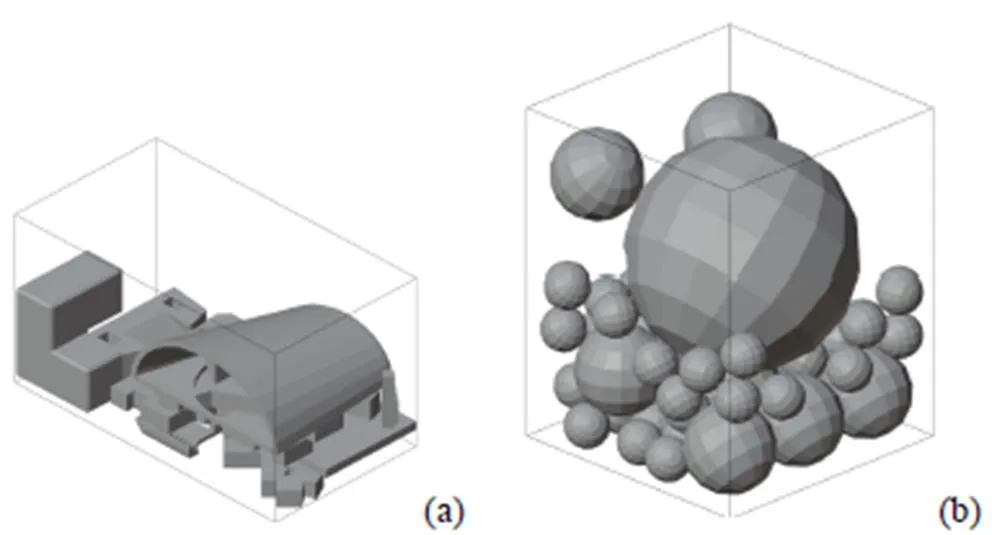
图4 A2018和Spheres的打包结果

图5 M2000的打包结果((a)测试1～10个长方体；(b)测试2～20个长方体；(c)测试3～30个长方体)

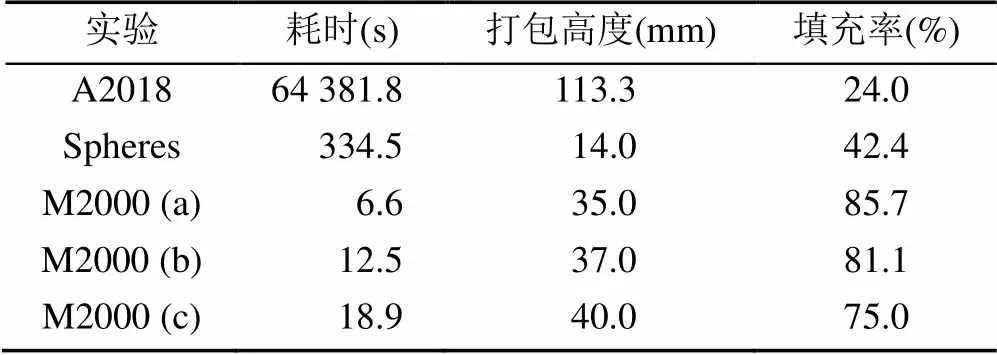
表5 实验3，4，5的打包耗时、高度和填充率

对比HAPE3D+SA，在表1和表2的前3个测试中，本文算法在打包高度上稍差一些。但在表2的第4个测试中，本文算法的打包高度优于HAPE3D+SA，并且观察表2可以发现，随着多面体数量增加，本文算法和HAPE3D+SA的差距逐渐减小到超过HAPE3D+SA。而结合表1和表4的数据来看，本文算法在耗时上远优于HAPE3D+SA，一般低2到3个数量级。

表1和表3还表明，本文算法的打包体积一般都R2018大，但随着多面体数量增加，差距逐渐减小。由于R2018无法加入容器尺寸的约束，本文算法在泛用性上具有一定优势。此外，表1和表4 表明，本文算法在耗时上明显优于R2018，一般低2到3个数量级。

A-HAPE3D是在本文算法基础上去除了Critic部分得到，表1和表2均表明，本文算法的打包高度都优于A-HAPE3D，并且随着多面体数量增加优势越发明显。而表14则意味着由于采用了相近的网络结构和计算流程，两者耗时比较接近。

在A2018，Spheres和M2000数据集上的结果展示了本文算法在实际应用中，以及在不同形状的多面体上的效果。从表5中可以看到，在M2000数据集上，本文算法在长方体数量较少且都体积较大时可以得到接近最优解的结果，但随着长方体数量增加以及小体积长方体的出现，本文算法得到的结果逐渐变差。

综合来看，尽管本文算法只在一个较小的训练集上进行训练，但在数据集L2015和S2004上都能得到较好结果，也能够成功运用于区别较大的数据集上，说明本文神经网络的泛用性是比较好的。

5 结束语

本文对强化学习在3DIP上的应用进行了探索和实现。首先介绍了近期的3DIP解决方案，简单分析了其优缺点，然后介绍与本文新算法相关的基础知识HAPE3D算法和Actor-Critic算法，之后提出了新算法AC-HAPE3D，并在5个数据集上验证了本文算法的有效性。本文算法尽管在5个数据集上均取得了一定的结果，但因神经网络架构对输出进行遮罩会使得神经网络在大的数据集上较难收敛，同时2个LSTM节点的设计也使网络的计算性能较差。未来可以考虑进一步优化神经网络的结构，尝试避免在输出上使用遮罩，同时可以尝试通过合并LSTM节点等方法来优化网络的性能。

[1] MARTELLO S, PISINGER D, VIGO D. The three-dimensional Bin packing problem[J]. Operations Research, 2000, 48(2): 256-267.

[2] CRAINIC T G, PERBOLI G, TADEI R. Extreme point-based heuristics for three-dimensional Bin packing[J]. INFORMS Journal on Computing, 2008, 20(3): 368-384.

[3] FANSLAU T, BORTFELDT A. A tree search algorithm for solving the container loading problem[J]. INFORMS Journal on Computing, 2010, 22(2): 222-235.

[4] LOH K H, GOLDEN B, WASIL E. Solving the one-dimensional Bin packing problem with a weight annealing heuristic[J]. Computers & Operations Research, 2008, 35(7): 2283-2291.

[5] ARAÚJO L J P, ÖZCAN E, ATKIN J A D, et al. Analysis of irregular three-dimensional packing problems in additive manufacturing: a new taxonomy and dataset[J]. International Journal of Production Research, 2019, 57(18): 5920-5934.

[6] IKONEN I, WILLIAM E, et al. Concept for a genetic algorithm for packing three dimensional objects of com- plex shape[C]//The 1st Online Workshop of Soft Computing. Nagoya: Nagoya University, 1996: 211-215.

[7] CAGAN J, DEGENTESH D, YIN S. A simulated annealing- based algorithm using hierarchical models for general three-dimensional component layout[J]. Computer-Aided Design, 1998, 30(10): 781-790.

[8] LIU X, LIU J M, CAO A X, et al. HAPE3D—a new constructive algorithm for the 3D irregular packing problem[J]. Frontiers of Information Technology & Electronic Engineering, 2015, 16(5): 380-390.

[9] WANG F, HAUSER K. Stable Bin packing of non-convex 3D objects with a robot manipulator[C]//2019 International Conference on Robotics and Automation. New York: IEEE Press, 2019: 8698-8704.

[10] WU H T, LEUNG S C H, SI Y W, et al. Three-stage heuristic algorithm for three-dimensional irregular packing problem[J]. Applied Mathematical Modelling, 2017, 41: 431-444.

[11] STOYAN Y G, GIL M, PANKRATOV A, et al. Packing non-convex polytopes into a parallelepiped[EB/OL]. [2022-05-19]. https://www.researchgate.net/publication/2569811_ Packing_of_Convex_Polytopes_Into_a_Parallelepiped.

[12] WOŁCZYK M. Deep learning-based initialization for object packing[J]. Schedae Informaticae, 2018, 27: 9-17.

[13] STOYAN Y, PANKRATOV A, ROMANOVA T. Quasi-phi- functions and optimal packing of ellipses[J]. Journal of Global Optimization, 2016, 65(2): 283-307.

[14] ROMANOVA T, BENNELL J, STOYAN Y, et al. Packing of concave polyhedra with continuous rotations using nonlinear optimisation[J]. European Journal of Operational Research, 2018, 268(1): 37-53.

[15] ART JR R C. An approach to the two dimensional irregular cutting stock problem[D]. Cambridge: Massachusetts Institute of Technology, 1966.

[16] VERKHOTUROV M, PETUNIN A, VERKHOTUROVA G, et al. The 3D object packing problem into a parallelepiped container based on discrete-logical representation[J]. IFAC- PapersOnLine, 2016, 49(12): 1-5.

[17] LAMAS-FERNANDEZ C, BENNELL J A, MARTINEZ- SYKORA A. Voxel-based solution approaches to the three- dimensional irregular packing problem[EB/OL]. (2022-05-04) [2022-05-26]. https://pubsonline.informs.org/doi/abs/10.1287/opre. 2022.2260.

[18] VERMA R, SINGHAL A, KHADILKAR H, et al. A generalized reinforcement learning algorithm for online 3D bin-packing[EB/OJ]. [2022-03-02]. https://arxiv.org/abs/2007. 00463.

[19] ZHANG J W, ZI B, GE X Y. Attend2Pack: Bin packing through deep reinforcement learning with attention[EB/OL]. [2022-06-18]. https://arxiv.org/abs/2107.04333.

[20] BHATNAGAR S, SUTTON R S, GHAVAMZADEH M, et al. Natural actor-critic algorithms[J]. Automatica, 2009, 45(11): 2471-2482.

[21] SUTTON R S, BARTO A G. Reinforcement learning: an introduction[M]. 2nd ed. Cambridge: MIT Press, 2018: 265-279.

[22] MATURANA D, SCHERER S. VoxNet: a 3D Convolutional Neural Network for real-time object recognition[C]//2015 IEEE/RSJ International Conference on Intelligent Robots and Systems. New York: IEEE Press, 2015: 922-928.

[23] HUBER P J. Robust estimation of a location parameter[J]. The Annals of Mathematical Statistics, 1964, 35(1): 73-101.

AC-HAPE3D: an algorithm for irregular packing based on reinforcement learning

ZHU Peng-hui, YUAN Hong-tao, NIE Yong-wei, LI Gui-qing

(School of Computer Science and Engineering, South China University of Technology, Guangzhou Guangdong 510006, China)

In areas such as 3D printing and express logistics, irregular packing results from the need to place parts or goods of different shapes in a defined space. A placement solution could be put forward, allowing as many polyhedra as possible to fit into a given container, or a batch of objects could be placed so closely together that they occupy the smallest volume, which is known as the irregular packing problem. This is an NP problem but is difficult to solve efficiently. This paper undertook the following investigation: placing a given set of polyhedra inside a 3D container with a variable dimension, so that the variable dimension of the packed container could be minimized. We proposed a reinforcement learning based algorithm, AC-HAPE3D. This algorithm could model the problem into a Markov process using the heuristic algorithm HAPE3D, and then utilize the policy-based reinforcement learning method Actor-Critic. We simplified the representation of state information by using voxels to represent containers and polyhedra, and employed neural networks to represent value and policy functions; to address the problem of variable length of state information as well as action space, we adopted a masking approach to masking some of the inputs and outputs, and introduced LSTM to handle variable length of state information. Experiments conducted on five different datasets show that the algorithm can yield good results.

irregular packing; heuristic algorithm; voxel; reinforcement learning; 3-dimensional printing

TP 391

10.11996/JG.j.2095-302X.2022061096

A

2095-302X(2022)06-1096-08

2022-08-02；

：2022-10-20

朱鹏辉(2000-)，男，硕士研究生。主要研究方向为计算机图形学。E-mail：347495867@qq.com

李桂清(1966-)，男，教授，博士。主要研究方向为数字几何处理与图像编辑。E-mail：ligq@scut.edu.cn

2 August，2022；

20October，2022

ZHU Peng-hui (2000-), master student. His main research interest covers computer graphics. E-mail：347495867@qq.com

LI Gui-qing (1966-), professor, Ph.D. His main research interests cover digital geometry processing and image editing. E-mail：ligq@scut.edu.cn