一道高联预赛四点共圆问题的探究

江西师范大学数学与统计学院 (330022)

陈德富 龚双波

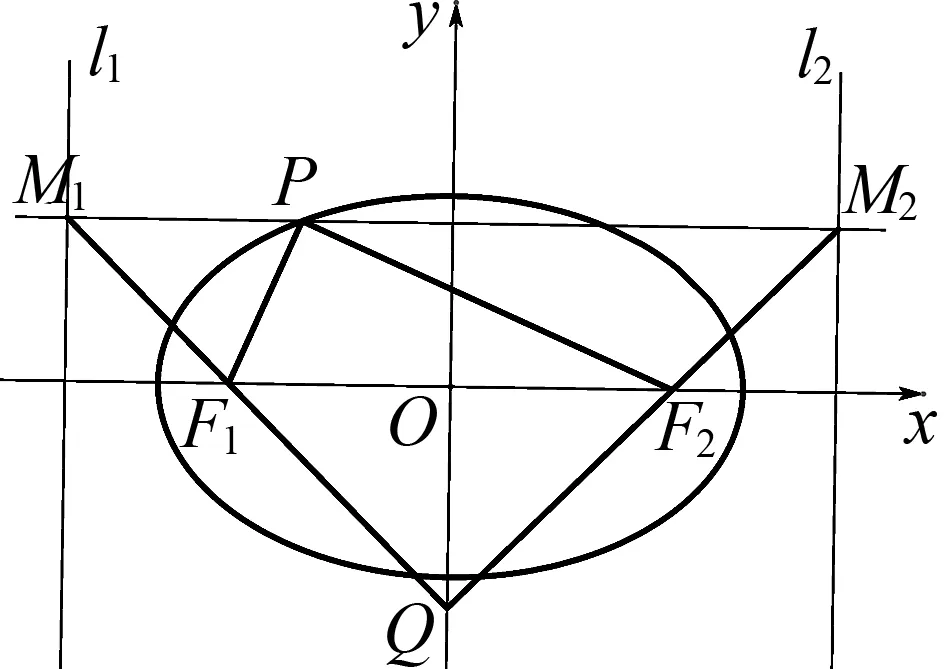
图1

题目如图1，设椭圆C的两个焦点为F1,F2,两准线为l1,l2,过椭圆上的一点P,作平行于F1F2的直线,分别交l1,l2于M1,M2,直线M1F1与M2F2交于点Q.证明:P,F1,Q,F2四点共圆.(2019年高中数学联赛江西预赛第10题)

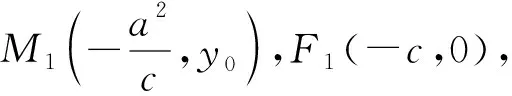
四点共圆由解析几何的代数计算来判定，思路有些单调.借助图形结构的几何性质和四点共圆的纯几何判定定理，我们可以从边长度的计算去得到结论.

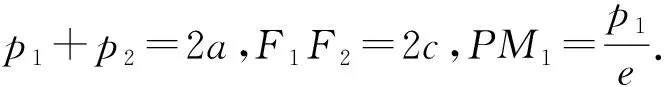
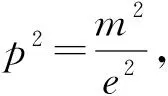
上面的证法充分发掘椭圆中线段比例关系的特殊性质，这些性质使得我们在处理托勒密定理和斯特瓦尔定理中边长运算时更加灵活便利,这表明借助几何定理，在解析几何中也能提高推理和计算的效率.

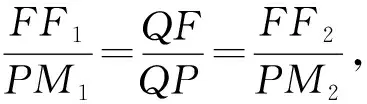
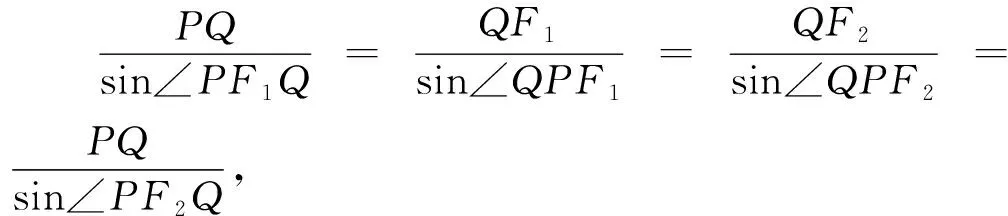
通过以上多种思路探究和推理论证,既丰富了我们的解题方法,也拓展了我们对问题的理解,这种基于基础知识的探究往往能很好提升知识灵活应用的能力,从而增强考场上的应变能力.另一方面,双曲线和椭圆都有双对称轴和两个焦点,通过计算,我们得到如下类似结论.

命题设双曲线C的两个焦点为F1,F2,两准线为l1,l2,过双曲线上的一点P,作平行于F1F2的直线,分别交l1,l2于M1,M2,直线M1F1与M2F2交于点Q.证明:P,F1,Q,F2四点共圆.

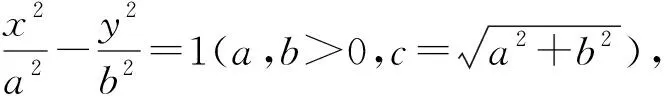
图2