一种用于高光谱图像分类的空谱协同编码方法

杨蕴睿， 郑东文

(1. 郑州工商学院工学院，河南 郑州 451400; 2. 河南科技大学信息工程学院，河南 洛阳 471023)

0 引 言

高光谱图像是一种包含丰富光谱波段的高维数据立方体。高光谱图像分类是一个重要的研究领域，其涉及到为每个观察到的像素向量指定一个唯一的标签。准确的高光谱图像分类和解译对于地物监测、国外军事、植被生长评估、污染检测等具有极其重要的意义。根据训练样本的不同要求，现有分类器主要分为无监督分类器和有监督分类器[1-2]。

无监督分类器不需要独立的训练过程，而是根据样本之间的相关性给每个样本分配特定的类别。在这方面，无监督分类器也被称为聚类方法，如K-均值[3]，模糊C-均值[4]。但这些方法具有复杂的初始化过程和有限的分类精度，因此相比有监督算法而言获得较少的关注。

相较于无监督分类算法，大多数现有的分类器集中在需要足够训练样本的有监督分类场景上。例如，传统的支持向量机（support vector machine,SVM）[5]利用训练好的最优超平面在特征空间中进行分类。此外还包括SVM的扩展算法，包括基于马尔可夫随机场的支持向量机(Markov random field-based SVM, MRF-SVM)[6]和基于复合核的支持向量机（composite kernel-based SVM, SVM-CK）[7]。现阶段，机器学习中的许多有监督算法也陆续被引入高光谱图像分类领域中，如稀疏编码。稀疏编码分类器（sparse coding classifier, SCC）[8]将训练样本视为字典并且并假设测试样本是字典中原子的稀疏线性组合而成。为了更好利用高光谱图像的空间光谱信息，Zhang等提出了一种联合测试样本空间邻域进行表征的联合稀疏模型，称为同步正交匹配追踪 （ simultaneously orthogonal matching pursuit,SOMP）[9]和另一种考虑光滑约束的正交匹配追踪算法（smoothing orthogonal matching pursuit, OMP-S）[9]。

相比于基于稀疏编码的分类器，基于协同编码的分类器（collaborative coding classifier, CCC）[10]采用L2范数对模型进行约束，并假定所有训练样本在样本表示中起着同等作用且不需要独立的训练过程。此外，相比SCC算法，CCC算法还具有两个明显优势：1)CCC具有解析解因此模型能更容易且更快被求解；2) CCC考虑训练原子的协同效应，因此对于小样本或具有类内光谱变异大的训练字典而言，CCC具有更优异的性能。为了增强测试样本和训练样本之间的相关性，Li等[11]提出了一种最近正则化子空间（nearest regularized subspace, NRS），它利用加权Tikhonov正则项来指定测试样本和训练样本之间的相关性。此外， Li和Du等[12]通过结合空间上下文，提出了NRS的一个扩展，称为联合协同表示（joint collaborative representation, JCR），其通过考虑测试和训练样本的空间上下文和训练样本测试样本间的光谱相似性来增强模型表示能力。为了同时获取稀疏表示和协同表示算法各自的优点，Li等[13]融合了残差域中的CCC和SCC，提出了融合表示分类器 (fused representation classifier, FRC)。为了充分利用空间信息，Li等[14]提出了一种结构感知CCC，它同时考虑训练样本的类标签信息和测试样本的光谱信息，以获得判别能力更强的表示系数。Jiang等[15]提出了基于空间感知的CCC，其在JCR基础上额外考虑基于空间的正则项以从空间光谱角度同时约束模型。为了考虑CCC算法在不同特征下不一样的分类性能，Li等[16]提出了基于多任务学习的CCC算法，该算法考虑图像所包含的光谱、光谱梯度、Gabor特征和形态学属性等特征。最新的相关工作还包括有Su等[17]提出的基于集成学习的协同编码方法，Shen等[18]提出的两阶段组协同编码方法，Zhou等[19]提出的空间峰值信息感知的协同编码模型。然而现阶段基于协同编码的算法对于图像空间光谱信息协同利用并不充分。此外在训练样本有限的情况下，现有算法的分类精度有限。

为了解决这两类问题，本文提出了一种空谱协同编码的分类器（spatial-spectral collaborative coding，SSCC）， SSCC算法首先对高光谱图像进行空间光谱加权滤波以去除图像中存在的噪声、异常像素和降低图像类内光谱变异。其次，SSCC算法通过获取测试样本和训练样本的空间相关性和光谱相似性并将该信息转化为空间光谱权重用来加权协同编码模型。在真实数据集上的实验数据表明所提出的SSCC算法优于其他典型的基于协同表示的算法，并且在训练样本较少的情况下仍具有较高的分类精度。

本文具有三个创新点：1）本文提出了一种空谱协同编码模型，该模型协同挖掘图像中具有的空间光谱信息以提升分类精度；2）本文提出了一种新的空间光谱加权滤波方法，该方法考虑每一个样本与其空间邻域像元的空间光谱相关性；3）本文提出一种新的加权正则项用于约束模型，该正则项通过考虑测试样本和训练样本之间的空间坐标欧式距离和光谱相似性来提升模型的分类精度。

1 空谱协同编码分类算法

1.1 标准协同编码算法

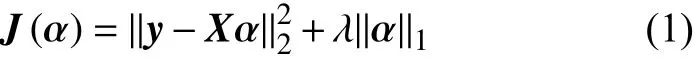
不同于基于L1范数约束的稀疏编码模型，协同编码模型考虑训练样本的协同特性，即所有训练样本都具有同等表征测试样本的能力。为了达到该目标，协同编码采用L2范数约束编码系数向量。模型可以表述如下：

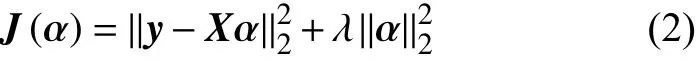
不同于式（1），式（2）是具有解析解的凸函数。通过对表示系数求导并令其为0，则可得模型的解析解为：

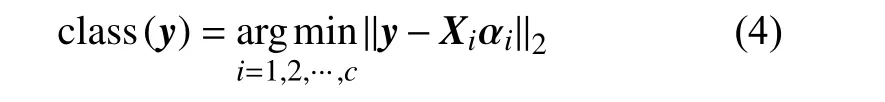
1.2 空谱协同编码分类算法(SSCC)基本原理与动机

现有协同编码分类器存在两个主要问题：1）空间光谱信息利用不充分，因此模型容易受噪声和类内光谱变异的影响；2）在小样本情况下，现有协同编码分类器分类精度有限。基于这两个问题，本文首先提出空谱加权滤波用于对每一个样本进行空间光谱平滑以去除噪声和光谱变异对分类的影响。其次，本文设计了一种空间光谱加权正则项以增强模型在分类时的判别能力。

图1详细描述了本文算法的分类流程。在步骤一及步骤二中，本文算法首先完成样本的分割与基于空谱加权的滤波过程。基于滤波的训练样本和测试样本，本文算法构建优化模型求解每一个测试样本在指定训练样本下的表示系数，即完成步骤三。基于测试样本所获得的表示系数，本文算法通过计算最小重构误差来获得测试样本的类别。即步骤四。

图1 SSCC 算法流程图

2.3节将详细介绍本文算法的具体原理与过程，涉及到空谱加权滤波的设计和优化模型的提出与求解过程。

1.3 空谱协同编码分类算法(SSCC)

1.3.1 空谱加权滤波

受限于高光谱传感器有限的空间分辨率，高光谱图像通常呈现出光谱变异强和信噪比低的情况，这对于图像的准确分类具有较大影响。另一方面，两个相邻像素通常被认为应该具有相似光谱特征。为了去除图像中潜在的噪声、类内光谱变异和异常像素，本文提出了一种空谱加权滤波方法。假定两个像素分别为给定窗口下的中心像素和其中一个邻域像素，且二者空间坐标分别为和，则定义和之间的空间几何权重如下：

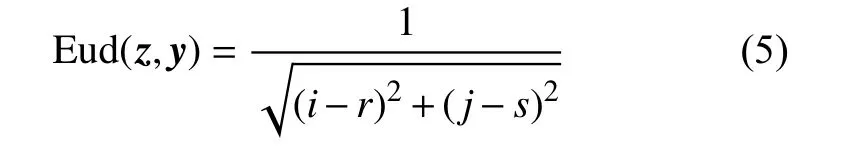
当中心像素和邻域像素空间相关性越强时，则二者的空间几何权重越大。此外，为了考虑中心像素和邻域像素之间的光谱相似，本文采用光谱角距离去度量光谱相关性，定义如下：

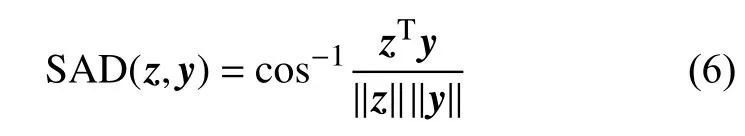
当中心像素和邻域像素光谱相关性强时，则光谱角距离小。为了同时融合光谱角距离和空间几何距离，本文对光谱角距离进行如下变换得到光谱相关性权重：

当中心像素和邻域像素光谱相关性强时，则光谱相关性权重大。联合式（5）和式（7），本文提出了空间光谱权重，定义如下：

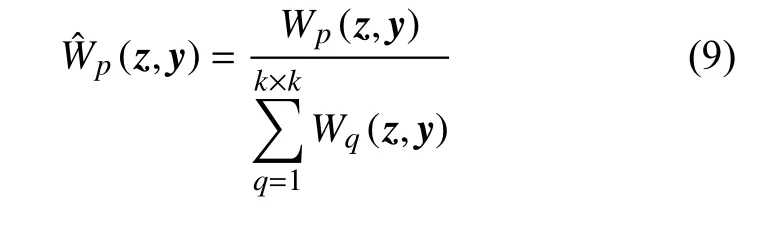
其中 Wp(z,y)表示窗口中第p个邻域像素的空谱权重，而 Wˆp(z,y)则表示第p个邻域像素经过归一化后的空谱权重。对于归一化后的权重，空谱加权滤波定义如下：

通过对所有给定的样本进行上述的空谱加权滤波，图像中所具有的噪声、类内光谱变异和异常像素能得到有效抑制，进而提升分类精度。通常而言，现有方法采用均值滤波对图像进行平滑以增强图像像元质量。但这类方法对图像不同类别地物边缘像元会形成较大的影响，因为边缘像元的邻域同质性较弱。本文提出的空谱加权滤波方法通过考虑每一个中心像元与其图像邻域像元的光谱和空间相关性，通过相关性来获得中心像元和邻域像元的重构权重，从而达到对中心像元进行滤波的目的。因此相比均值滤波方法，本文提出的空谱加权滤波能有效减弱像元信息的损失。

1.3.2 空谱加权正则项

对于给定的测试样本，协同编码假定其可以被训练样本线性表示，然后根据最小重构误差来给测试样本分配类别。在此之中，不同训练样本内在地和测试样本具有不同的相关性。从光谱信息的角度来讲，和测试样本具有同样类别的训练样本应该光谱相似。从空间信息的角度来讲，和测试样本具有同样类别的训练样本应该在空间坐标上更为接近。因此，本文提出的SSCC算法提出了基于空间光谱信息的权重。对于给定的测试样本 y ∈ RL×1和训练样本中第l 个训练原子 xl∈ RL×1，假定二者的空间坐标为和，则二者的空间光谱相关性权重定义如下：

当测试样本和某一训练原子相关性非常高时，二者的空间光谱相关性权重则相应较小，从而迫使训练字典所对应的表示系数越大。通过考虑所有训练样本和给定测试样本的空间光谱相关性权重，本文所提出的SSCC算法定义了如下的空间光谱加权正则项:

1.3.3 空间光谱协同编码算法 SSCC

本文所提出的SSCC算法首先采用空谱加权滤波算法对测试样本及训练样本进行滤波以去除噪声对模型的干扰，其次采用空谱加权正则项对模型进行有效约束以提升模型分类精度。通过采用式（10）对测试样本和训练样本进行空谱加权滤波并融合式（2）和（12），本文提出的SSCC算法基本模型如下：

令式（14）导数为0，则模型的解析解可以表述如下：

1.4 SSCC分类算法步骤与伪代码

2 实验结果与分析

本文实验均运行在配备有16 GB RAM，酷睿I7的台式机电脑Matlab平台上，其中Matlab版本为2016a。

2.1 对比算法

为了从多个角度验证SSCC算法性能，本文采用7种标准算法进行实验对比。7种算法包括传统机器学习算法SVM和SVM-CK，稀疏编码的算法SRC和SOMP， 和协同编码算法CRC、JCR和FRC。对于分类结果，本文采用4种评价标准进行评价，分别为：类别精度（class accuracy, CA），总体精度（overall accuracy， OA），平均精度（average accuracy，AA）, 和Kappa系数。所有算法分类结果在四种评价标准上数值越高时说明分类效果越好。在本文的实验中，所有算法均进行10独立运行，最终实验结果取10运行的平均结果。

2.2 对比算法与评价指标

本文采用两种标准真实高光谱数据集来度量算法的有效性。数据一为Indian Pines 数据集，该数据集由机载红外成像光谱仪拍摄并包含有145×145个像素和200个经过选择的波段。此外该数据集包含有16个地物类别，且空间分辨率为20 m。数据二为 University of Pavia 数据集，该数据集由反射光学系统成像光谱仪在意大利Pavia大学拍摄而成。该数据集具有1.3 m的空间分辨率并包含103个波段和610×340个像素以及9个地物类别。图2给出了两个数据集的可视化图像（第100波段）以及两个数据集对应的真实地物分布。图3和图4分别展示了 Indian Pines和 University of Pavia 图像的标签信息。

图2 Indian Pines数据集和University of Pavia数据集及其真实地物分布

图3 Indian Pines数据集标签信息

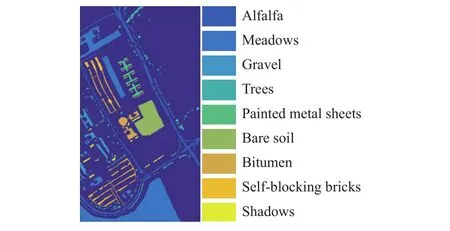
图4 University of Pavia数据集标签信息

2.3 参数对分类结果的影响实验

为了度量不同参数的选择对模型存在的潜在影响，本试验首先衡量了所提出的SSCC算法在两种数据集上的参数影响实验。在Indian Pines数据集上，本实验选取了每类5%的样本作为训练样本，并且的选择范围为{1×10-5, 5×10-5, 1×10-4, 5×10-4,1×10-3, 5×10-3, 1×10-2}。如图 5 所示，当在所选择的范围内变化时，模型分类的OA精度变化较小，但整体呈现出先上升后下降的趋势，当为固定在1×10-3时，模型具有最优结果。

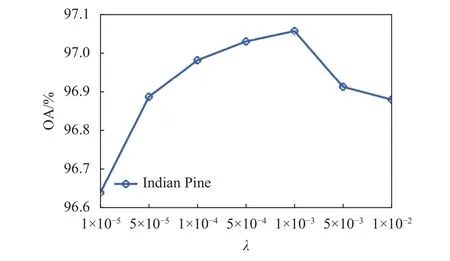
图5 参数的选择对模型在Indian Pines的分类结果的影响

在 University of Pavia 数据集上，本实验从数据集中每类各选取30个样本作为训练集，的变化范围为{1×10-7, 5×10-7, 1×10-6, 5×10-6, 1×10-5, 5×10-5,1×10-4}。最终的参数对分类精度的影响趋势如图6所示。由图可知，参数对SSCC模型在该数据集上分类精度的影响趋势与其在Indian Pines数据集上类似，即精度呈现先上升后下降的趋势且当为5×10-6时，模型呈现最佳的分类精度。

图6 参数的选择对模型在University of Pavia的分类结果的影响

为了验证模型在采用不同窗口大小k下的空谱加权滤波效果，本试验将窗口k从1变化到11以观测分类精度变化趋势。其中当k=1时，说明SSCC算法不执行滤波过程。图7展现了SSCC算法在两个数据集上不同窗口k下的分类精度。图中两个曲线均呈现出随着窗口大小增加，精度先上升然后趋于平缓的趋势。对于 Indian Pines和 University of Pavia两个数据集而言，当施加空谱加权滤波时，相对于没有施加空谱加权滤波的模型，精度分别最多能获得8%和6%的提升，这证明了所提出的空谱加权滤波模块对SSCC算法性能提升的有效性。

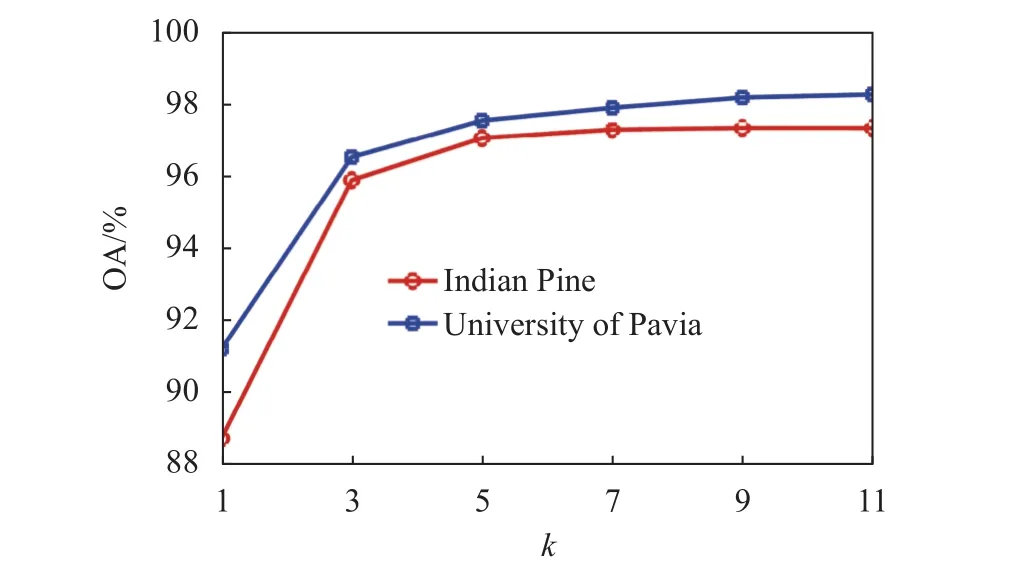
图7 窗口大小的选择对模型在两个数据集上分类结果的影响

2.4 SSCC算法在Indian Pines数据集上的分类性能

本试验旨在对比所有算法在Indian Pines数据集上的分类精度以验证所提出的SSCC算法的性能。对于Indian Pines，选取的训练集是从每类各随机选取10%训练样本。表1给出了所有算法在Indian Pines数据集上的16类分类结果和总体评价精度。如表所示，对于16类地物，SSCC算法能提供其中15类地物的最佳分类精度，而其他对比算法中仅SVM-CK和JCR算法能提供第8类和第11类地物的最佳分类结果。对于总体精度而言，SSCC 算法能提供最佳OA、AA和Kappa结果。

表1 不同算法在Indian Pines数据集上的分类精度和标准差

从OA精度提升效果来看，SSCC算法在Indian Pines上的OA结果比SVM、SVM-CK、SRC、SOMP、CRC、JCR和FRC算法分别具有18.42%、10.33%、26.26%、3.57%、29.64%、 4.99%和 25.73%的有效提升。由本试验可知，SSCC算法能有效提升分类精度。

从表中可以进一步观测出，部分类别数量是严重不平衡的，如#1，#7，#9类分别仅含有5个，3个和2个训练样本。但对于这类小样本问题，所提出的SSCC算法依然能提供最优的分类精度。

图8展现了所有分类算法的分类效果图和真实地物GT的可视比较。由图可知，SSCC算法所生成的分类图相比其他算法更少出现错分，且分类结果图和GT较为一致。

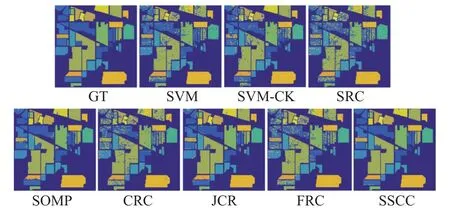
图8 本文所考虑的算法在Indian Pines数据集上的分类图

2.5 SSCC算法在University of Pavia数据集上的分类性能

本试验旨在对比所有算法在 University of Pavia数据集上的分类精度以验证所提出的SSCC算法的性能。对于 University of Pavia 数据集，从每类各随机选取60个样本作为训练集。由表2可知，对于 University of Pavia数据集，所提出的 SSCC 算法仍然能在9种地物中的7类地物提供最佳分类结果，而对比算法中仍然仅SVM-CK和JCR算法能分别提供第4、第5、和第9类地物的最佳分类。此外，所提的SSCC算法也能提供最好的OA、AA和Kappa结果。此外，SSCC算法在 University of Pavia上的OA结果比SVM、SVM-CK、SRC、SOMP、CRC、JCR和FRC算法分别具有 13.99%、8.89%、20.92%、19.78%、32.37%、4.52%、21.3%的有效提升。图9展现了所有分类算法的分类效果图和真实地物GT的可视比较。

图9 本文所考虑的算法在University of Pavia数据集上的分类图

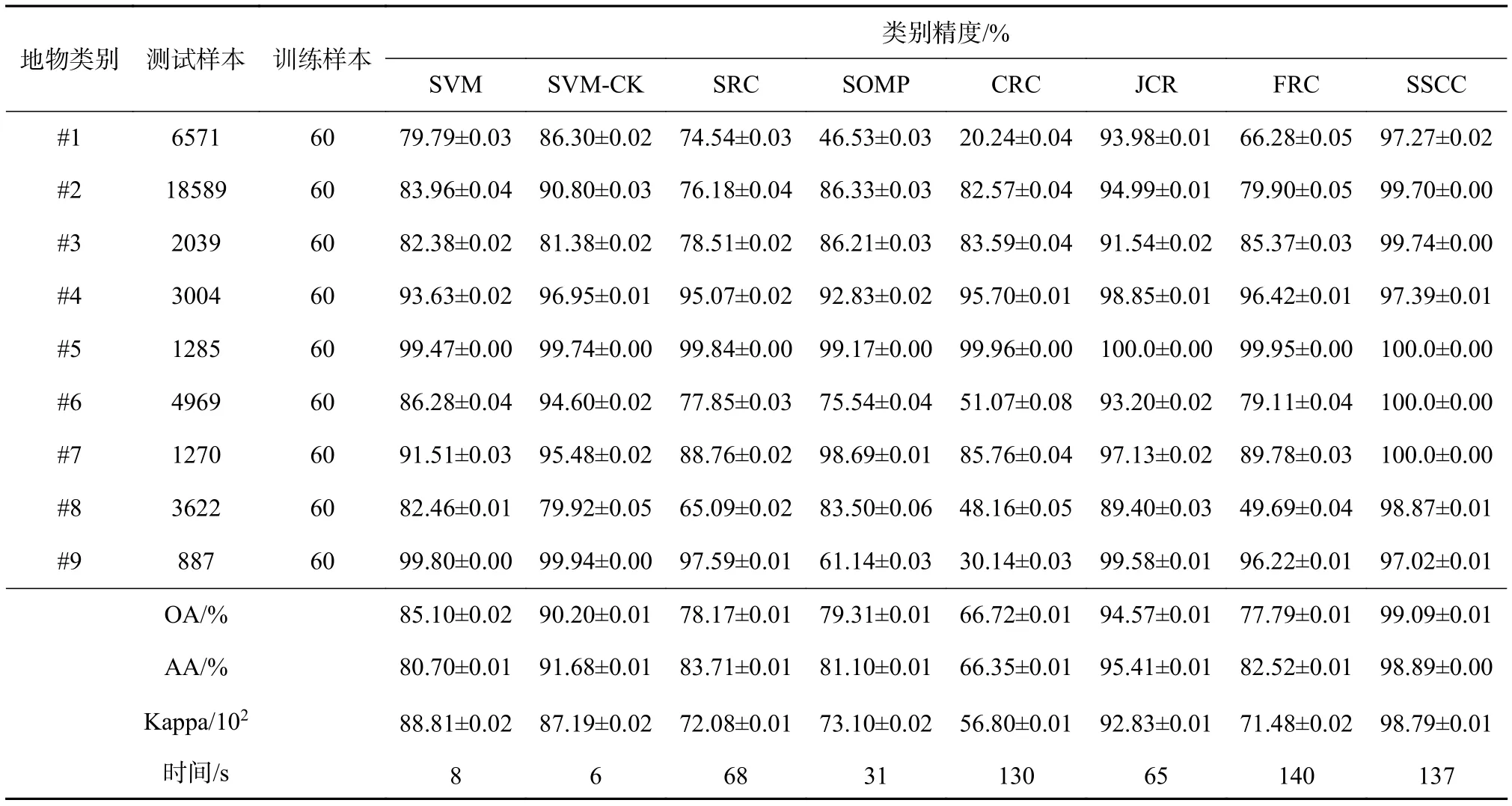
表2 不同算法在University of Pavia数据集上的分类精度和标准差

2.6 不同数目的训练样本对SSCC算法在两种数据集上分类性能的影响

为了度量不同训练样本比例对模型分类精度的影响，本实验测量了所有分类器在两个不同数据集上不同比例训练样本场景下的分类性能。对于Indian Pines数据集，从每类选取的训练样本比例分别为{1%, 2%, 3%, 4%, 5%, 6%, 7%, 8%, 9%, 10%}。图 10（a）（b）（c）分别展现了所有算法在 IndianPines数据集上不同比例训练样本下的OA、AA和Kappa系数的精度变化趋势。由图可以看出当训练样本比例逐渐升高时，算法的精度逐渐上升，但相比其他对比算法，所提出的SSCC算法在所有比例的训练样本场景下均能提供最佳的分类精度。

对于 University of Pavia 数据集，本试验从每类选取的训练样本数目分别为｛10, 20, 30, 40, 50,60｝。如图 11（a）（b）（c）所示，随着训练样本数目的增加，所有分类算法精度包括OA、AA和Kappa系数均呈现逐渐上升的趋势，但对于SSCC，其可以在不同数目的训练样本集下均保持最优的分类精度。

在小样本情况下，从图10、图11可同时观测到，当训练样本场景是每类1%的训练样本的Indian Pines数据集或每类10个训练样本的University of Pavia数据集的极端条件下，SSCC算法相比其他分类器仍具有明显优势。本试验说明，所提出的SSCC算法能有效处理高光谱图像小样本场景下的分类问题。

图10 算法在Indian Pines数据集不同训练样本比例下的实验结果

图11 算法在University of Pavia数据集不同训练样本数量下的实验结果

2.7 SSCC算法与其他编码算法的差异性度量

为了度量分类器之间在不同数据集上的统计差异，本实验验证了所提出的SSCC算法和其他先进的稀疏编码和协同编码分类结果的McNemar测试[20]。当 McNemar测试的|z|值分别大于1.96和2.58时，说明两个分类器分别在95%和99%的置信水平上是统计独立的。表3给出了SSCC算法和SRC、SOMP、CRC、JCR和FRC算法的统计值。如表3所示，SSCC和其他编码分类器的|z|值远远大于2.58，这说明所提出的SSCC算法和其他先进的稀疏和协同编码算法具有明显统计差异，也同时说明所提出的SSCC算法相比现有的基于编码的算法具有明显的算法差异。

表3 两个分类器在标准McNemar测试上的统计差异

3 结束语

本文提出了一种基于空谱协同编码的高光谱分类方法。该方法对测试样本和训练样本首先进行基于空谱加权的滤波以去除潜在的噪声和高类内光谱变异性。此外在求解测试样本表示系数的优化模型时，本文算法进一步考虑测试样本和训练样本之间的空间光谱相关性正则项。在Indian Pines和University of Pavia真实高光谱数据集上的实验表明本文提出的方法在联合空间光谱信息的情况下能有效提升分类精度。相比现阶段典型的编码方法，本文算法在两种数据集上能分别获得98.82%和99.09%的总体精度。此外，在小样本的情况下，如每类1%训练样本的Indian Pines数据集和每类10个训练样本的 University of Pavia 数据集下，本文算法均能获得90%左右的总体精度。

基于实验结果，与现有研究对比，本文算法优势及创新点在于：考虑训练样本和测试样本的空间光谱相关性来进行样本的去噪和约束优化模型以获得高性能的分类模型。因此本文算法能有效应用于卫星对地观测遥感图像的数据解译领域中。需要注意的是本文算法假定训练样本来源于观测图像中，因此可以完成对训练样本的空间光谱信息提取。但实际上，遥感图像训练样本的获取成本较高，很难从一幅大尺度的遥感图像中获得高质量且数目多的训练样本。因此，未来的研究方向将更加关注训练样本的数据增强和小样本学习。