基于EEMD-LSTM方法的光伏发电系统超短期功率预测

卢忠山， 袁建华

(三峡大学电气与新能源学院，湖北 宜昌 443002)

0 引 言

随着传统化石能源的日益紧缺和环境污染问题的日益严重，清洁可再生能源，特别是太阳能得到了大规模的开发和利用[1]。在光伏发电系统中，发电功率主要取决于天气情况，但天气情况类型各异、数量差异巨大，个别地区天气突变较快，使得发电功率的波动较大，给电力系统的安全稳定运行带来了挑战[2-3]。因此，研究太阳能的波动特性，在1 h或更短的时间内获得精确的超短期光伏功率预测，有助于电网部门通过预测值确定实际发电量的不足来确定必要的备用发电容量，对于促进光伏电站融入电力系统，提高电网的安全性和稳定性具有重要意义[4-5]。

一般来说，光伏发电功率的预测主要有物理预测模型和统计模型两大类。物理预测模型利用太阳辐照度预报值，结合光伏电池板倾角以及电站所处位置等信息，按照光伏功率的物理成因建立模型[6]。文献[7]使用传统光伏电池的数学模型进行建模，增加了光辐射强度对温度的修正，从而对传统模型进行了改进。文献[8]选取5种参数模型，对光伏器件的仿真模型进行测试，利用新的组合方法对模型求解。文献[9]利用传感器收集光伏阵列和气象站上的相关数据，提出一种可对学习速率进行回溯调整的预测算法，提高了模型的收敛速度。

统计模型依托光伏电站历史功率数据，分析多种外界因素对发电量的影响，最后建立输入与输出的映射模型实现光伏功率的预测[10]。文献[11]提出了一种基于小波变换和深度卷积神经网络的混合模型，该模型基于比利时光伏发电农场的光伏输出时间序列数据。计算结果表明，所提供的预测模型的平均误差在季节、预测期和光伏发电位置方面优于其他模型。文献[12]提出了一种基于深度循环神经网络-长短期记忆神经网络的SPV光伏发电负荷预测模型，并证明了该模型与传统的支持向量机工具相比性能良好。文献[13]利用深度信念网络预测短时间光伏发电的输出功率。该模型的输入变量为太阳辐照度、大气压力、相对湿度和过去4天太阳输出功率数据。文献[14]利用气象数据和历史光伏输出数据作为输入，训练和测试深度神经网络，提出了一种高精度的基于DNN的“PVPNet”模型来预测24 h光伏系统输出功率。文献[15]提出了一种深度deep-RNN模型预测一天中每小时的太阳辐照度水平。

以上研究取得众多成果，但两类方法都存在部分局限性。物理预测方法需要依托详细的电站及历史气象数据信息，且计算过程中容易产生偏差，导致预测结果不理想。统计模型方法在建模时更为简单快捷，但部分模型难以收敛，且多数统计模型并未根据天气类型将不同天气下的光伏功率分别预测，而天气类型对光伏发电功率影响较大。为更好地提高模型的预测精度，本文将天气变化情况分为非突变天气及突变天气两大类，利用EEMD分解法对光伏电站历史数据进行模态分解，将相关性较强的分量送入高精度的LSTM神经网络。为验证所提模型预测精度，建立BP、SVM、KNN和LSTM共4种模型与所提模型进行比较，比较结果清楚地表明了所提出预测方法的有效性。

1 光伏出力影响因素

本文选用某光伏发电系统2017年1月1日-2017年12月31日整年的光伏功率数据，每天采集52个样本点。仅选择光伏功率稳定输出的时段（08:00-18:00）进行分析，不同天气下光伏发电功率如图1所示，当天气较为稳定时，晴天天气光伏发电功率最高，其他依次是多云、阴天和雨雪天气。稳定天气，光伏系统功率波动较小，输出较为稳定，整体接近抛物线。突变天气情况下，光伏发电功率波动较大，此时对整个电网的稳定运行有较大的影响。因此，区分天气类型对于光伏发电功率预测意义重大。

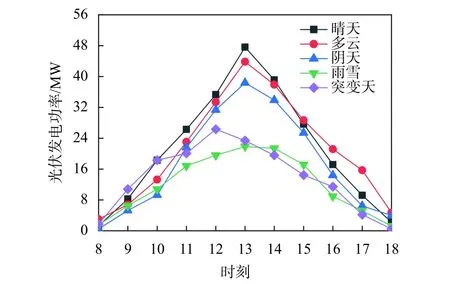
图1 不同天气下光伏发电功率

统计光伏电站历史功率数据可知，输出功率不仅与天气类型有关，而且受温度影响。图2是28 d内每天14：00的光伏发电功率与温度对比情况，第1 d、2 d、3 d 均为晴天，但发电功率略有差别，即温度可影响光伏发电系统功率。但整体而言，光伏系统功率变化趋势与温度变化趋势大致相同。

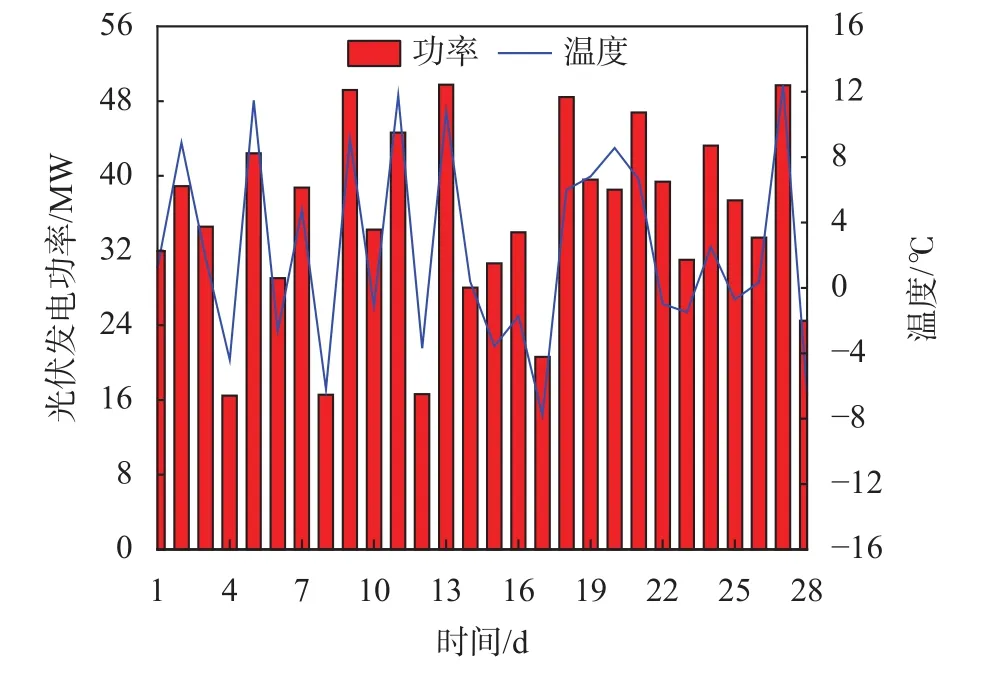
图2 光伏发电功率与温度对比图

2 EEMD和LSTM预测方法

当光伏发电输出功率波动较大时，预测模型的精度会受到影响，故采用EEMD分解法对历史数据进行模态分解。

2.1 EEMD分解

2.1.1 EEMD 分解原理

EEMD分解混叠法主要是为了综合改善类似经验模态分解法(EMD)中的模态混叠现象，是在EMD分解法的基础上改进而来的一种新的模态分解法[16]。EEMD分解法将光伏功率数据加入高斯白噪声之后进行多次EMD分解，然后对分解出来的IMF分量进行一个总体上的平均化定义。在原始信号中加入高斯白噪声有效改善了模态混叠问题。由于EEMD法是在EMD法的基础上改进而来，故EMD分解次数M与高斯白噪声幅值k直接影响模型的预测精度。本文经过多次调试参数值，最终取M值为150，k值为0.25。

EEMD分解流程如下：

1）向信号内部加入幅值为k=0.25的正态高斯噪声，设置EMD分解次数M=150，迭代次数m=1。

2）开展第m次EMD分解。EMD分解流程为：

①发电功率的数据序列中加入高斯白噪声得到新的功率序列为：

式中：x(t)——发电功率的原始数据序列；

m——添加白噪声的次数；

qm(t)——高斯白噪声；

xm(t)——新的功率序列。

②对新的功率序列xm(t)进行EMD分解，得到n个IMF分量和1个剩余分量：

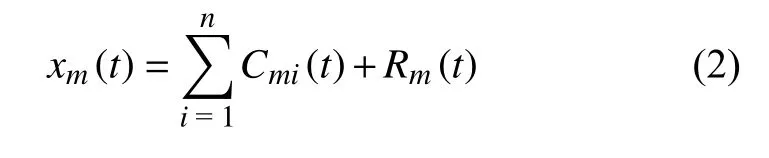
式中：Cmi(t)——第m次分解得到的第i次IMF分量；

Rm(t)——剩余分量。

3）计算得到各个分解量的均值：

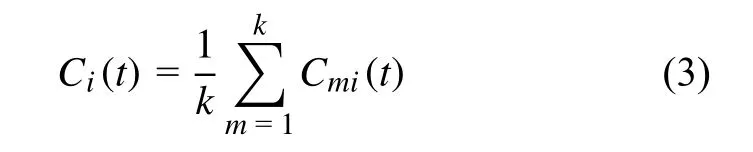
其中Ci(t)为分解的最终结果。

4）输出EEMD的分解量。

2.1.2 EEMD 分解结果

采用EEMD法对光伏输出功率序列分解，得到IMF1～IMF5和剩余分量。分解后的功率序列如图3所示。第一行为光伏原始输出功率，IMF1～IMF5为分解后序列，最后一行为剩余分量。观察分解后的序列可知，IMF1～IMF5分量整体波动趋势呈现出一定的相似性，但波动的细节有所不同。IMF1～IMF5和剩余分量加入其他气象因素作为LSTM模型的预测条件。

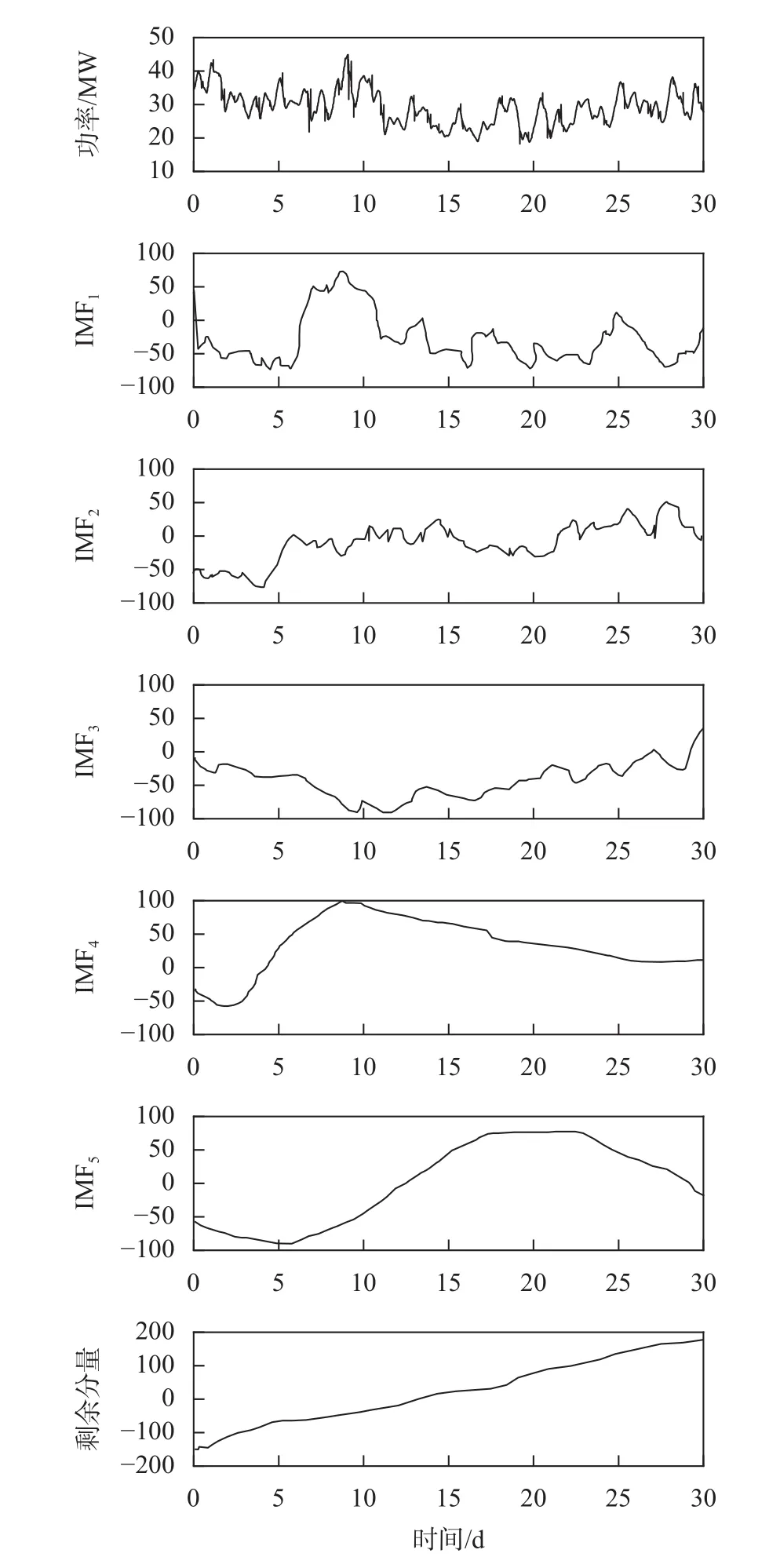
图3 功率序列分解结果

2.2 长短期记忆神经网络

长短期记忆神经网络[17]作为一种循环逻辑神经网络的特殊变体，它的拓扑结构在充分保留传统的循环反馈机制功能的同时，通过引进门控单元的方式来控制信息累计和增减的速度，包括用户有选择地添加新的信息以及遗忘先前已经累计和增减的信息，彻底解决了功率序列建模中普遍存在的长期依赖性问题。

LSTM拓扑神经网络同样由输入控制层、输出控制层和隐含层组合构成，与传统的RNN网络相比，LSTM神经网络的隐含层使用门控记忆模块替换普通的输入神经元，拓扑结构如图4所示。

图4 LSTM记忆模块结构

门控记忆模块单元是LSTM系统结构中最重要的核心组成部分，其在某一特定t时刻的记忆状态记为ct，包涵了该记忆序列的一些长期性的记忆数据信息。隐含层在某一特定时刻t的记忆状态ht包含了该记忆序列的一些短期性的记忆数据信息。前者的记忆数据周期更新率远远要低于后者。整个记忆模块通过输入门、输出门和遗忘门实现。

在某一时刻，LSTM中一个记忆单元模块的输入主要包括：序列输入xt、隐含层前一个时刻的状态ht-1及记忆单元前一个时刻的状态ct-1；记忆单元模块的序列输出主要包括：该时刻隐含层的状态ht和记忆单元状态ct。输入门控制xt对ct的影响程度；输出门控制ct对ht的影响程度；遗忘门控制和处理记忆单位中的历史数据信息。三者的计算公式如下式：

式中：it、Wt、bt——输入门的计算结果、权重矩阵和偏置项；

io、Wo、bo——输出门的计算结果、权重矩阵和偏置项；

ft、Wf、bf——遗忘门的计算结果、权重矩阵和偏置项；

在t时刻记忆模块输出结果为ct与ht，公式如下式所示：

tanh——双曲正切激活函数；

Wc——输入单元权重矩阵；

bc——输入单元状态偏执项；

·——按元素相乘。

2.3 EEMD-LSTM耦合模型

光伏电站的功率序列受多个气象因素的影响，是典型的非线性、非平稳信号，为此本文提出EEMD-LSTM耦合模型。该模型通过EEMD分解将功率序列分解为一系列IMF分量，筛选出强相关的子序列送至不同深度的LSTM网络，最后将子序列预测结果重构得到最终预测结果，模型结构如图5所示。

图5 EEMD-LSTM模型框架结构图

具体建模流程如下：

1）EEMD 分解

通过EEMD分解法将信号x(t)分解为5个IMF和剩余分量Rn。

2）IMF 分量提取

计算IMF分量和剩余分量Rn与x(t)的Pearson相关系数，记为 P ={p1,p2,···,pn}。将Pearson相关系数和的1 / (2(n+1))作为相关系数阈值p0，其中n为IMF分量个数和剩余分量Rn个数之和。

其中pi表示两个连续变量的Pearson相关性系数。

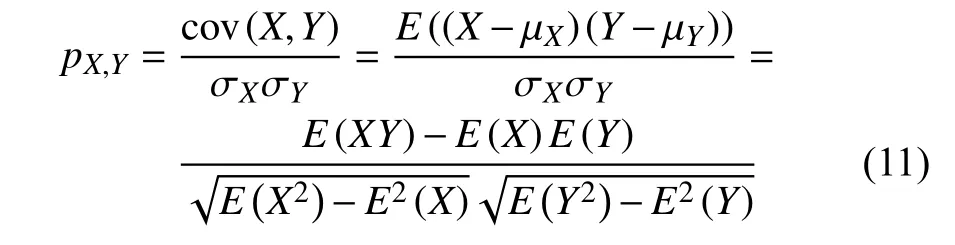
由式（11）可知，pi大小在-1～1 之间，当 pi的绝对值接近1时，表现为具有强相关性；当pi的绝对值接近0时，则被称为无相关性。根据阈值p0可筛选出相关性较大的IMF分量或Rn分量。

3）LSTM网络预测

为避免功率序列经过EEMD分解后不同量纲带来的影响，将筛选出来的相关性较大的分量进行归一化处理后，输入至LSTM神经网络得到子序列预测结果。将子功率预测分量反归一化后进行叠加得到最终的光伏功率预测结果。

本文采用的LSTM模型结构如图6所示，为一阶两层的结构，模型的具体参数设置如下：训练次数设置为1 000次，LSTM层节点数设置为50，批大小设置为72，选取平均绝对误差函数作为损失函数，adam作为优化函数，tanh作为激活函数。由于数据量较大，为缓解过拟合现象，设置Dropout为0.2。

图6 LSTM模型结构图

3 光伏电站功率预测模型

3.1 建模分类依据

搭建EEMD-LSTM预测模型对光伏发电系统功率进行超短期（15 min）预测。根据天气因素分类指标，将天气情况分为非突变天气和突变天气两大类。由于光伏发电系统在突变天气和非突变天气情况下输出功率有较大区别，所以本文搭建EEMDLSTM预测模型对两类天气分别进行预测。同步建立BP、SVM、ANN、LSTM 4种单一模型与所提模型进行计算精度对比。

选择希尔不等系数eTIC、均方根误差eRMSE和平均绝对百分比误差eMAPE对模型精度进行评价，表达式如式（12）～（14）所示。eTIC介于 0～1之间，系数越小表明预测功率和真实功率之间的差异越小，预测精度越高。当eTIC=0时，表示预测功率曲线和真实功率曲线完全拟合。eRMSE用来评价功率预测值与真实值之间的偏差，对功率序列中特大误差反映较为敏感。eMAPE常用于时间序列的预测，用来衡量预测模型的准确度，eMAPE值越小，预测精度越高。

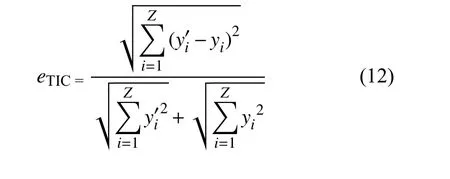
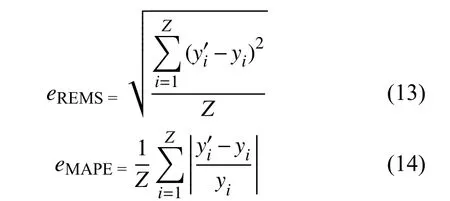
式中：Z——测试样本数目；

y′ ——光伏输出功率的预测值；

y——光伏输出功率的实际值。

使用BP、SVM、ANN和LSTM单一模型对光伏功率进行预测时，直接将气象因素作为输入量，光伏功率作为输出量。

3.2 预测流程

基于EEMD-LSTM模型的光伏发电系统超短期功率预测流程见图7。将天气情况分为突变天气和非突变天气两大类。由图1可知，突变天气时光伏电站的输出功率波动较大，该电站输出功率最大时刻为午间14:00左右，故将该时刻的输出功率进行EEMD模态分解，使之成为平稳的输出功率序列。非突变天气细分为晴天、多云、阴天和雨雪4种天气类型，将不同天气类型光伏发电系统的历史功率数据进行EEMD模态分解，对分解后的IMF1～IMF5和剩余分量加入不同的气象因素作为LSTM模型的预测条件。在搭建预测模型时，在原始功率序列中加入150组k=0.25的高斯白噪声，对新的功率序列进行150次EEMD模态分解。

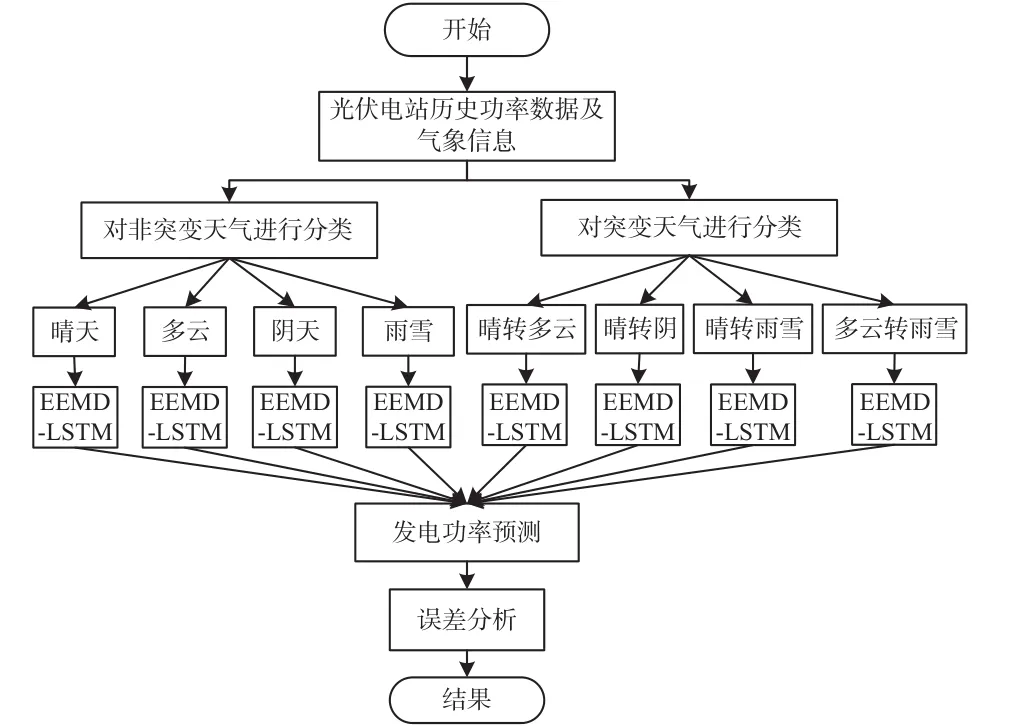
图7 预测流程图

4 算例分析

利用目前收集的某光伏发电系统2017年整年的天气及功率数据验证EEMD-LSTM模型的有效性，并分别对突变天气以及非突变天气进行预测验证。数据来自于同一大型光伏发电系统，总装机容量约50 MW。选取光伏功率稳定输出的时段（08:00-18:00）进行预测。根据数据统计情况，该光伏电站所在地区 2017 年中晴 139 d，多云 50 d，阴31 d，雨雪 67 d，突变天气 78 d。非突变天气中以晴天和阴天为例进行分析，在139 d的晴天数据中，选取 120 d 作为训练样本，19 d 作为测试样本；31 d 的阴天天气中，26 d作为训练样本，5 d作为测试样本。验证突变天气预测准确性时，选择晴转雨雪天气为例进行分析，其中14 d作为训练样本，2 d作为测试样本。

1）晴朗天气光伏功率预测结果如图8所示，预测误差如表1所示。在晴朗天气情况下，光伏输出功率曲线波动较小，功率变化具有一定的规律性。除SVM模型外，其余4种模型均呈现出较好的预测效果。分析eMAPE、eRMSE、eTIC3个指标可以发现，所提的EEMD-LSTM预测模型的误差均小于单一预测模型，且在午时，功率曲线出现轻微波动时，单一模型预测的准确性略有降低。对比单一预测模型，所提EEMD-LSTM预测模型整体上能更好地贴近实际功率曲线，拟合效果最佳。

表1 晴朗天气光伏功率预测误差

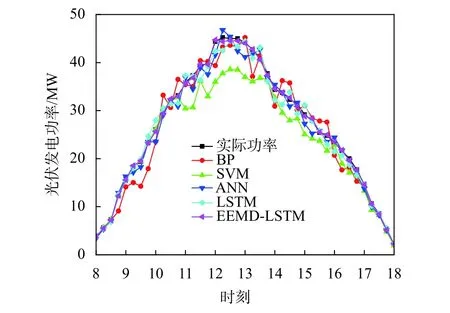
图8 1月8日晴天光伏功率预测结果

2）阴天天气光伏输出功率预测结果如图9所示，误差如表2所示。在阴天天气情况下，受多种气象因素影响，光伏输出功率曲线波动较大，各模型的预测功率与实际功率产生偏差，其中BP神经网络和SVM的预测误差明显增大，而EEMDLSTM模型经过集合经验模态分解减小了功率数据波动对模型精度的影响，在天气状况发生波动时段改善了模型的预测性能。在4月2日阴天天气下，EEMD-LSTM的 eMAPE值相较于 BP、SVM、ANN和 LSTM分别降低了 0.148、0.259、0.13和 0.047，即EEMD-LSTM模型性能较好，预测准确度最高。

表2 阴天天气光伏功率预测误差

图9 4月2日阴天光伏功率预测结果

3）突变天气预测结果如图10所示，误差如表3所示。天气发生突变后，BP神经网络的预测功率明显低于实际功率，准确度难以保证。在2 d的突变天气情况下的BP、SVM和ANN 3种预测模型误差较大。EEMD-LSTM模型较LSTM模型的eMAPE值分别降低0.091和0.048，EEMD分解在一定程度上改善了模型预测性能。对比晴朗天气和阴天天气误差指标，突变天气的预测误差虽略有变大，但EEMD-LSTM模型的预测效果仍是最好的。

图10 2月20日突变天气预测结果

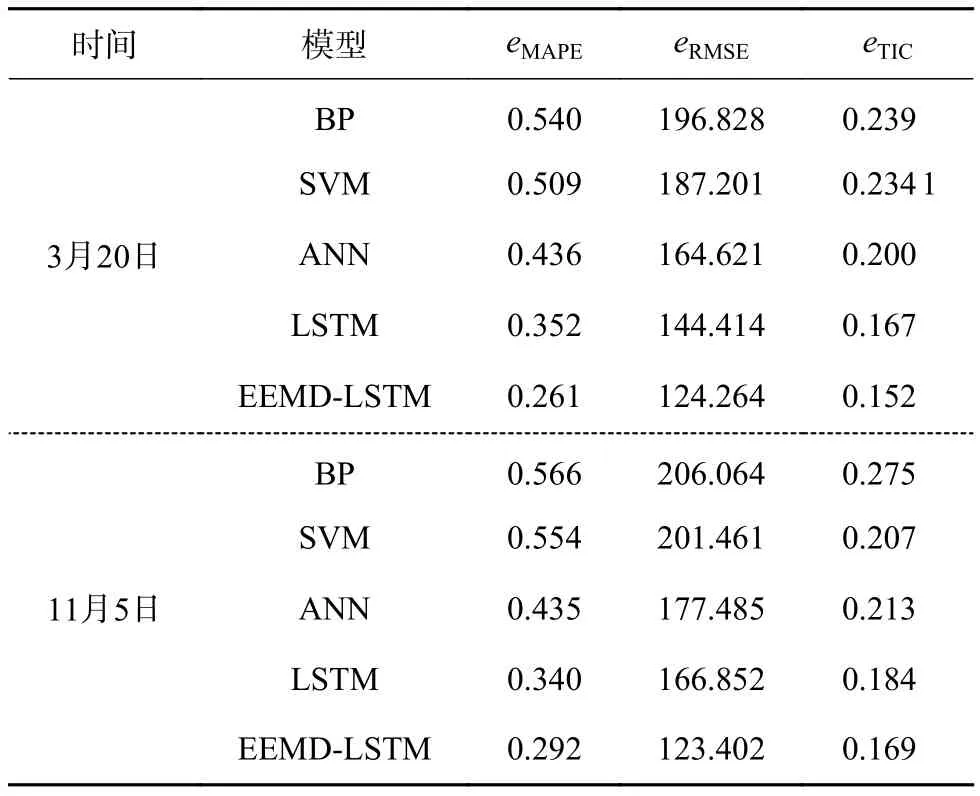
表3 突变天气光伏功率预测误差

本文统计了该光伏电站所有测试样本的预测值和有效值，分别在LSTM和EEMD-LSTM两种不同的算法下评估其eRMSE、eMAPE和eTIC，结果见表4。

表4 LSTM和EEMD-LSTM预测误差对比

对比LSTM预测模型的表现，EEMD-LSTM耦合模型在eRMSE、eMAPE、eTIC上分别提升了21.23%、11.92%、25.67%，即光伏输出功率曲线数据经过EEMD模态分解后，使得LSTM预测算法更加精准。

5 结束语

文章对天气类型进行划分，提出基于EEMDLSTM方法的光伏功率超短期预测模型，直接对输出功率数据进行EEMD模态分解，找出数据局部特征进行功率预测，建立4种单一模型与所提模型进行对比，并根据eMAPE、eRMSE、eTIC评价预测误差。所提模型解决了传统预测方法在功率波动时准确性低的问题。主要结论如下：

1）光伏输出功率具有较大的随机性，特别是天气类型对光伏输出功率的影响较大。

2）将光伏输出功率曲线数据进行EEMD模态分解，通过提取曲线细节分量，充分表征曲线的局部特征，使得LSTM预测算法更加精准，EEMDLSTM模型较LSTM模型在eRMSE、eMAPE、eTIC上分别提升了21.23%、11.92%、25.67%；而BP和SVM模型结构较为简单，在各类天气下都表现出较大误差，不适合光伏功率序列的预测；ANN模型在功率波动较大的突变天气下准确度难以保证。

3）经过晴天、阴天及突变天气的预测结果可知，EEMD-LSTM模型预测的精度满足光伏发电系统输出功率的超短期预测要求，其预测的功率与实际功率差值较小，预测误差值不影响系统正常工作。