滚转角差异对高升阻比外形侧向力影响的 天平校准方法研究
2023-01-12吕治国赵荣娟
吕治国,赵荣娟,黄 军
(中国空气动力研究与发展中心超高速所,绵阳,621000)
0 引 言
在航空航天飞行器发展的过程中,通常需要进行风洞试验,在风洞试验时,主要利用天平测量作用在模型上的气动力[1,2],针对不同风洞试验设备,发展了多种形式的天平[3~6],为了降低测量的不确定度[7~10],准确测量气动力,形成了天平相关标准或规范。天平发展的同时,在世界范围内,也发展了多种形式的天平校准系统[11~14],以及与天平和校准系统相适应的天平校准的数据处理方法[15~17]。在激波风洞等脉冲型风洞设备上主要利用压电天平进行飞行器气动力测量试验[18~21],为了提高测量结果的可信度,在风洞测量试验前,需要对天平进行校准。
在中国空气动力研究与发展中心的压电天平的校准中,天平支杆尾部承载锥段安装在天平校准台转接件上,由于加工误差,相对于天平体轴系而言,通常天平会存在一个小滚转角,在实际校准中这个小滚转角对干扰系数(特别是纵向对横向干扰系数,如法向力分量对侧向力分量或法向力分量对偏航力矩分量干扰系数)校准结果的影响较大,会导致在天平不同安装轮次校准中,天平法向力分量对测向力分量干扰系数差异较大,从而导致在高升阻比模型六分量气动力测量中,小侧向力分量测量值异常。为了解决这个问题,首先想到的就是消除天平校准和风洞试验的安装滚转角差别,为此在试验准备期间,先将天平安装到风洞上,准确测量天平的滚转角,在天平校准时,测量天平校准的安装滚转角并调整到风洞试验安装滚转角一致,由此设计并加工了滚转角调节装置[22]和压电天平校准加载套[23],解决了小侧向力测量结果异常问题,但实施该项措施比较繁琐,除了在天平校准前多一次将天平安装到风洞上进行测量滚转角环节外,在校准时测量和调整天平的滚转角也是一个非常繁琐和漫长的过程,严重影响天平校准和风洞试验准备的效率。
经过对小滚转角如何影响天平法向力分量对侧向力分量干扰进行研究,本文提出了一种通过调节滑轮高度改变加载线与天平形成的滚转角度,实现对天平加载滚转角变化的校准方法[24],从而获得天平法向力分量对侧向力分量干扰系数随滚转角变化的函数关系,并利用天平校准对该方法进行了验证。
1 小滚转角对天平法向力分量对侧向力分量干扰的影响
天平法向力分量对侧向力分量干扰(俯仰力矩对侧向力干扰类似),如图1所示,由于小滚转角存在,在校准天平法向力分量对侧向力分量干扰时,也就是在法向力方向校准(采用负方向卸载方式)的时候,砝码载荷在侧向力分量上有个投影分量,这个投影分量值为mgsinγ0,假定侧向力主系数为KZZ以及法向力分量对侧向力分量干扰系数为KNZ,天平法向力分量对侧向力分量干扰输出为VNZ,法向力分量对侧向力分量干扰输出(这里暂不考虑其他分量对侧向力干扰,同时为了简化,系数均取绝对值,不失一般性,考虑天平处于γ0滚转角下进行法向力分量校准,同时这个滚转角也可代表天平校准和风洞试验中天平安装滚转角差异),当无滚转角时,天平法向力分量对侧向力分量干扰输出为VNZ为
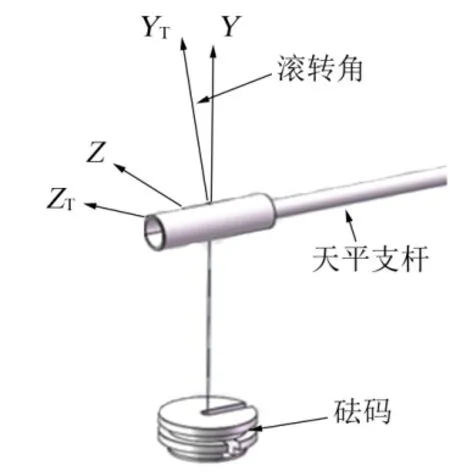
图1 天平校准安装坐标系示意 Fig.1 Diagram of Balance Calibration Mounting and It's Coordinate System

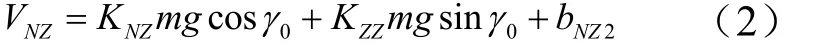
式(1)和(2)中,1NZb和 2NZb均为天平校准输出信号随砝码质量变化曲线的截距,改写式(2)为
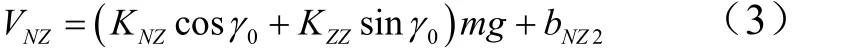
式(1)和式(3)等号右端第1项,也就是KNZ和( KNZcosγ0+ KZZsin γ0),可认为是关于砝码载荷校准直线方程的斜率项,可利用线性拟合获得。显然,在有滚转角情况下,如果还认为式(3)中括号内还是法向力对侧向力干扰系数(记为 K'NZ)的话,会带来相对较大的误差,分析如下:
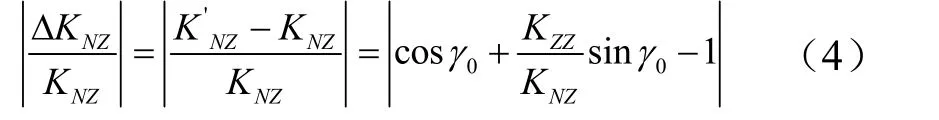
压电天平主系数与干扰系数比值通常处于40~200范围内,假定=40,对于γ0为10′或30′,则由式(4) 计算出天平法向力分量对侧向力分量的干扰系数相对误差,分别可以达到11.64%和34.90%;如果=200,同样对于γ0为10′或30′,其相对误差分别 可以达到58.18%和174.53%。显然,对于高精度六分量气动力测量来讲,不能接受这样的相对误差。 对于式(4),可从另一个方面来理解,以滚转角为变量计算其相对误差,如果限制KNZ相对误差在0.5% 以内,也就是≤0.005同样对于=40,可以接受的γ0≤0.42′,对于=200,可以接受的γ0≤0.08′。 换句话说,只要滚转角大于0.42′,法向力分量对侧向力分量干扰系数误差就会大于0.5%;如果控制这个误差小于0.5%,通常要求这个滚转角小于0.08′,这个要求是非常苛刻的。
2 小滚转角影响校准方法研究和验证
由上节的计算分析可知,为了消除滚转角对天平法向力对侧向力分量干扰系数的影响,也就是将法向力对侧向力干扰系数的相对误差控制在0.5%以内,需要将滚转角误差调整到小于0.08′,在校准天平时,这样的调整非常困难。此外,即使在天平校准时将这个滚转角度调整到小于0.08′,但在风洞试验测量中,模型支撑机构的小滚转角误差同样存在,并且调整消除小的滚转角误差也异常困难,为了降低小滚转角误差对天平校准和风洞试验测量的影响,同时提高风洞试验效率,本文提出了一种校准天平法向力对侧向力干扰系数随滚转角变化方法,采用该方法,在天平校准和风洞试验中,只需要测量出滚转角而不需要大费周折将滚转角调整到0°或调整滚转角使风洞试验与天平校准时滚转角一致。
校准天平法向力对侧向力干扰系数随滚转角变化原理如图2所示,将高度可调节的滑轮安放在天平的侧面,使得加载线与天平轴线(XT)垂直,同时形成滚转角度可以随滑轮升降变化的加载校准系统,将天平固定安装在校准台上,通过变化滑轮高度实现加载力矢量与天平轴线相对滚转角度变化,获得滚转角变化与天平法向力对侧向力干扰系数的对应关系,为了验证方法以及获得天平分量间干扰系数,对两台压电天平进行了验证性校准,在每台天平校准前,仔细调整天平的安装姿态,确保天平轴线水平,同时调整加载线与滑轮高度,确保加载线水平,并与天平轴线垂直,下面分别介绍这两台天平的校准情况。

图2 加载滚转角变化影响天平校准示意 Fig.2 Diagram of Rolling Angle Influence in Balance Calibration
YDTP1202压电天平(简称1202天平)校准验证时,加载点与滑轮上端的距离约为2930 mm,在加载线处于水平位置时,变化加载砝码质量,进行第1轮次法向力加载基准校准;此后,将滑轮降低5 mm再进行第2轮次校准,此后每轮次降低5 mm,共进行4轮次校准。
针对每一次滑轮高度的变化,以砝码质量变化(模拟法向力加载变化)为自变量,采用线性拟合(首次利用)求出天平侧向力分量输出值(在没有施加侧向力情况下就是法向力对侧向力干扰输出值)的线性方程分别为

式中 m为砝码质量;g为重力加速度。
占用、盗用电网调度信息传递网络的事情屡有发生,这些占用和盗用电网调度信息传递网络的做法一部分是电力系统内部员工借助职务之便私自使用,另一部分是外来的一些不法分子借助高科技手段盗用电网调度系统的信息传递网络。这些做法一方面导致了网络的拥堵,影响信息传递的速度,另一方面也带来了一些安全隐患。
由于钢丝水平位置长度约为2930 mm,当滑轮降低高度为Δh,求出加载钢丝角度相对初始滚转角(为便于数据处理和画图,不妨假定为0)变化情况因此,滑轮高度变化-5 mm, -10 mm,-15 mm,对应的加载角度相对滚转角0°变化分别为-0.0017,-0.0034,-0.0051(以弧度为单位,下同),这些角度变化可以等同于天平滚转角相对初始滚转角变化的角度,以滚转角变化为自变量,以法向力分量对侧向力分量的干扰系数,也就是式(5)至式(8)中对应的斜率项为因变量,再次利用线性拟合,可以较容易求出法向力分量对侧向力分量干扰系数随滚转角变化的函数关系式如下:

由于式(9)是天平法向力对侧向力分量干扰系数随加载角度变化拟合直线,因此,可以认为KNZ=4.6527是天平在本次安装时,加载角度为零时拟合值,也就等价为天平在初始滚转角时最佳拟合值。很显然,天平以不同滚转角度安装,其KNZ是不相同的。进一步分析,当天平在风洞试验中,安装滚转角为Δγ1时,KNZ=-210.5175 Δγ1+4.6527。也就是说:只要测量出天平在风洞试验中的安装滚转角,风洞试验时天平法向力对侧向力分量的干扰系数就确定了。
对于YDTP1001压电天平(简称1001天平)的校准和验证过程以及数据处理与1202天平类似,在此不再赘述,这里仅将结果列出:
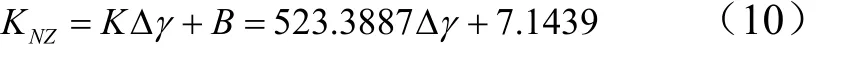
式(9)和式(10)的意义在于,风洞试验和天平校准中,只要测量出了天平的安装滚转角,即可计算得出在风洞试验和天平校准两个环节中安装滚转角的差异,将此差异利用式(9)和式(10)函数关系式,可避免繁琐和严格的天平安装、测量和调整滚转角的过程。采用式(9)和式(10)后,减少了天平校准前安装到风洞上测量天平安装的初始滚转角的环节,同时也不需要将校准的滚转角调整与风洞试验的滚转角一致,仅仅保留了测量天平在校准和风洞试验中滚转角差异的过程,显然采用本文的天平校准方法后,可以简化风洞试验天平的安装环节,提高天平校准和风洞试验准备的效率。
式(9)和式(10)中截距项就是代表天平没有滚转角情况下1202天平和1001天平的 NZK的值,如果Δγ01=30′时,NZK分别为-2.8156和11.7113,分别与没有滚转角的 NZK值相比较,1202天平和1001天平 NZK的相对误差分别可达到60.5%和163.9%,这样的相对误差显然是不可接受的。
对式(9)和式(10)进一步分析,可以获得更有意义的结果,当1202和1001两台天平对应的加载线偏转角分别为Δγ01=0.0221和Δγ01=-0.0136时,两台天平的法向力分量对侧向力分量干扰系数均为KNZ=0。显然,在天平校准或风洞试验中,如果能将两天平的滚转角分别调整安装到这两个角度,天平法向力分量对侧向力分量的干扰系数KNZ为零。基于同样的考虑,采用类似的方法,获得类似式(9)或式(10)的滚转角变化与法向力分量对偏航力矩分量干扰系数的关系式,即可以获得类似式(9)或式(10)干扰系数为零时分别对应的Δγ02的值,当然,这个值与前述通过式(9)或式(10)获得的Δγ01可能不一致,可以对两个角度取平均值 Δγ=( Δγ01+Δγ02)/2,在天平校准或风洞试验中,将天平的滚转角调整安装到接近γΔ这个角度,这样调整后,可以将天平法向力分量对侧向力分量以及法向力分量对偏航力矩分量两个干扰量降到最低(不是单一干扰最低),由此可以综合降低风洞试验天平侧向力分量和偏航力矩分量测量的不确定度。
3 结 论
本文提出了一种改变加载线与天平滚转角度,实现变化小滚转角条件下进行天平法向力分量对侧向力分量干扰系数校准,通过两台天平的验证校准研究,可以获得如下初步结论:
a)校准时天平安装的滚转角对天平法向力对侧向力分量干扰系数影响较大,天平校准必须要确定或消除安装滚转角的影响,从而获得准确的干扰系数。
b)通过改变加载线与天平轴线形成的滚转角度,进行天平法向力分量对侧向力分量干扰系数的校准,除了可以获得相对较准确的天平侧向力主系数KZZ外,还可以获得天平法向力分量对侧向力分量干扰系数随滚转角变化的函数关系式,风洞试验时测量出天平安装时真实的滚转角,就能利用获得的函数关系式得到天平在风洞试验时的干扰系数,由此可以简化风洞试验天平的安装环节,提高天平校准和风洞试验准备的效率。
c)采用改变加载线与天平轴线形成滚转角变化的校准方法,进行法向力分量对侧向力和偏航力矩分量的干扰系数校准,可以分别获得两个干扰系数为零时对应的两个小滚转角,风洞试验测量中将天平安装滚转角调整到接近两个小滚转角的平均值,可以将天平法向力分量对侧向力和偏航力矩分量的干扰综合降到最低,由此可以降低风洞试验天平侧向力和偏航力矩分量测量的不确定度水平。
