六种边界等直梁模态特性和振动响应的解析分析
2023-01-12马斌捷周书涛洪良友梁吉鹏王丽霞
马斌捷,周书涛,洪良友,梁吉鹏,王丽霞
(北京强度环境研究所,北京,100076)
0 引 言
等直梁振动响应问题统一模型最一般化的边界条件为两端有不同附加质量和弹簧约束,包括带不同附加质量、转动惯量、不同刚度的线性和转动弹簧,总共含有8个影响参数。由于该模型边界条件的复杂性,其特征方程具有复杂的四阶行列式,内含的8个影响参数各不相等,使得振型函数得不到简化,不易获得等直梁振动特性和响应的解析解。当等直梁的端部约束为零和无穷大时,边界条件可以简化为简支、固支和自由3种。等直梁两端的这3种边界总共有9种排列、6种组合。此时,等直梁振动问题特征方程中的端部约束参数可以消除,简化为三角函数和双曲函数的组合方程,振型函数和广义质量的待定系数可以简化或者变为零,从而可得到形式较为简洁的等直梁振动特征方程及振动响应解析解。
在采用理论分析方法获得梁振动响应解析解方面的研究相对较少。Li[1]考虑两端支座横向和转动激励,得到了受轴向力作用Euler Bernoulli梁的动态响应解析解。Li和Ren[2]采用Galerkin截断法和模态叠加法,解析研究了受三向移动载荷作用水平曲梁垂向、扭向、径向和轴向的动态响应。Yu等[3]基于模态叠加法和Euler Bernoulli梁理论,给出了放置在粘弹性地基上、在任意激励作用下双截面梁挠度、速度、加速度、弯矩和剪力的显式解析表达式,并在集中、冲击2种载荷下验证了梁振动响应的解析解与数值解。上述文献均未进一步给出广义质量的解析表达式。马斌捷等[4]提出了可显著简化广义质量计算难度的特征变换方法,解决了端部带约束悬臂梁振动响应的解析求解问题,并指出该方法可用于解析求解各种边界条件和端部约束(包括平动与转动的质量与弹性约束)等直梁的广义质量,奠定了解析求解等直梁振动响应的基础。
有鉴于此,本文采用特征变换方法,基于非归一化的简洁振型函数形式,获得了6种边界条件下等直梁广义质量的解析结果。针对不同载荷分布,给出了各种响应参数动态放大系数的解析表达式和计算曲线。此外,基于广义质量解析解推导了模态有效质量的解析算式,充实了振动理论的方法和内容。
1 等直梁的模态特性和广义质量
各种边界条件等直梁(见图1)的横向弯曲振动微分方程为[5]
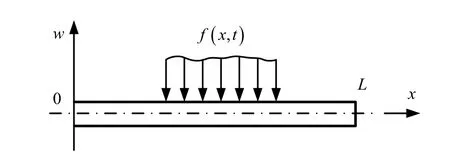
图1 等直梁振动响应示意 Fig.1 Vibration Response Sketch of Uniform-section Straight Beam
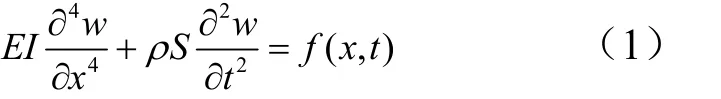
式中 0 x L≤≤;E,I,S,ρ,L分别为梁的材料弹性模量、横截面轴惯性矩、密度、截面面积和长度;f (x, t)为梁单位长度上作用的分布力。在自由振动时f (x, t)=0,式(1)可以简化为

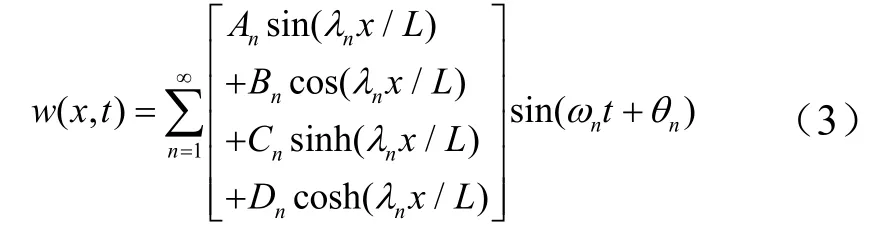
等直梁两端的简支、固支和自由边界条件共有9种排列、6种组合,可以分为3种对称(两端简支、两端固支、两端自由)和3种不对称(简支-固支、简支-自由、固支-自由)边界。Ginsberg[6]给出了等直梁这6种边界的模态特性。其中,两端简支等直梁的特征方程为

模态叠加法是获取梁振动响应的基本方法。在特征值和振型函数已知的基础上,计算各阶振型对应的广义质量和广义力,可以得到各阶广义位移响应,再结合振型函数(含双曲函数和三角函数)可获得物理位移响应。振动响应解析分析的基础是广义质量和广义力有解析表达式。由于双曲函数与线性函数的乘积以及三角函数与幂函数的乘积均有解析积分式,因而各种边界条件下集中力、均布力和线性分布力存在广义力的解析表达式。然而等直梁广义质量以往只有两端简支边界条件下有解析表达式,马斌捷等[4]采用特征变换方法给出了端部带约束悬臂梁广义质量的解析表达式。本文采用特征变换方法进一步给出6种边界条件等直梁广义质量的解析表达式。
特征变换方法的核心是引入特征值条件kn= mnωn2,将各阶广义质量拆分为50%的广义刚度除以固有频率平方与50%的广义质量之和,利用振型函数与振型曲率函数的平方和,抵消多项反号函数,从而显著简化广义质量积分的解析求解过程。
等直梁第n阶广义质量 nm和广义刚度nk分别为
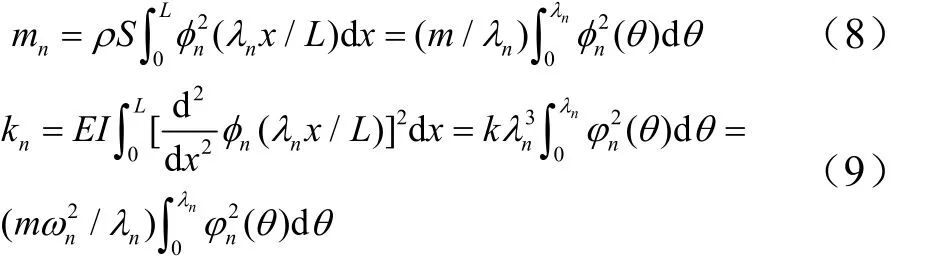
式中 m,k分别为梁的质量和刚度,m = ρSL,k = EI /L3;φn(θ),φn(θ)分别为振型函数和振型曲率函数。按照特征变换法将广义质量 nm的表达式改写为[4]
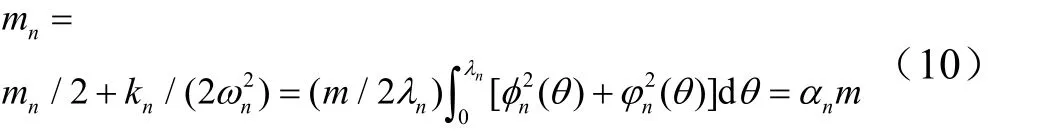
根据式(10),采用简洁振型表达式,本文得到了含简支(两端简支、简支-固支、简支-自由)边界等直梁的振型函数和振型曲率函数表达式分别为

不含简支(悬臂、两端固支、两端自由)边界等直梁的振型函数和振型曲率函数表达式分别为

由此可以进一步得到等直梁广义质量的解析表达式。含简支边界等直梁广义质量系数的表达式为

将相应含简支边界条件的特征方程和振型 系数代入式(15),可得到:

由式(16)可得:两端简支梁的广义质量系数为0.5;简支-固支和简支-自由梁的广义质量系数为0.4996(1)n=、0.5(1)n>,均非常接近0.5。
对于3种不含简支边界等直梁,其广义质量系数的表达式为
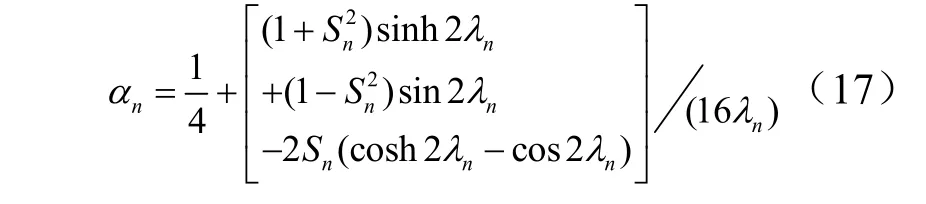
将相应不含简支边界梁的特征方程和振型系数代入式(17),可得到:

由此可以看出,采用特征变换方法推导得到的含简支梁的广义质量系数基本为0.5,不含简支梁的广义质量系数均为0.25,结果非常简洁。
上述广义质量解析解的获得,解决了获取等直梁振动响应解析解的关键问题。
由特征值条件,等直梁的各阶广义刚度nk可写为
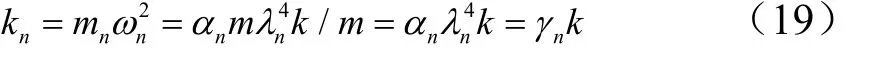
式中nγ,nα分别为广义刚度系数和广义质量系数,γn=,与αn成正比。
2 广义力和动态响应放大系数
等直梁上作用的单频线分布压力()p x对应的广义力nF为
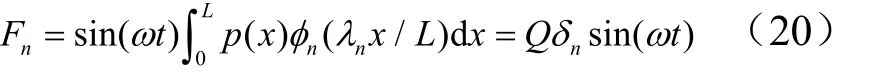
式中 δn为广义力系数,为合力。对于作用在梁上 xO= ζL (0 ≤ζ ≤1)处的集中力Q sin(ωt)、作用在全梁上的均布力(Q /L) sin(ωt)和线性分布力 (2Q /L2)x sin(ωt),对应的广义力系数分别为
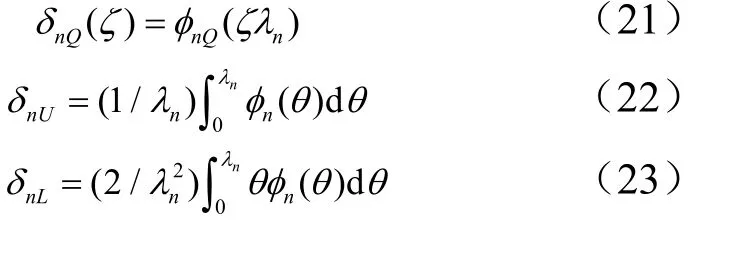
双曲函数与线性函数的乘积以及三角函数与幂函数的乘积均有解析积分式[7,8],因而可以得到均布力和线性分布力广义力的解析积分结果。计算结果显示:
a)对于两端自由梁,均布力和线性分布力对应的广义力只能产生刚体平动和转动,不会引起振动响应;对于简支-自由梁,线性分布力对应的广义力只能产生刚体转动,也不会引起振动响应。
b)集中力的广义力系数不随阶次增大而产生有规律的变化;均布力的广义力系数随阶次增大而降低,大致与特征值成反比;线性力的广义力系数随阶次增大而降低,变化趋势介于与特征值成反比和与特征值平方成反比之间。
c)对称边界条件下,偶数阶中部( /2x L= )振型曲率为零,使得中部截面弯矩响应也为零;对称载荷的偶数阶广义力均为零;偶数阶广义力需要施加非对称载荷;线性力与均布力的中部响应动态放大系数相同。
d)线性力的高阶广义力较低,集中力的高阶广义力较大,施加不对称集中力易激励出偶数阶高阶振动响应。
e)在0.3 L和0.7 L处作用的集中力能产生除10 n阶次的广义力,可产生较多阶次的响应。
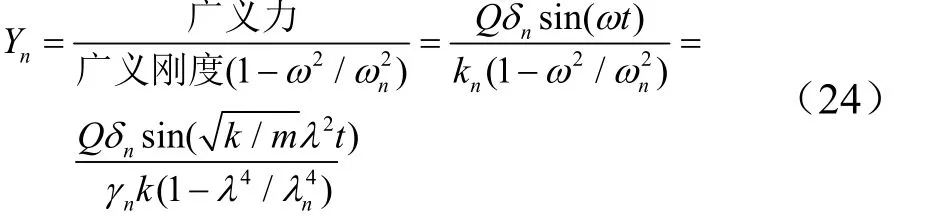
单频外力激励下位移响应(,)w x t的表达式为:
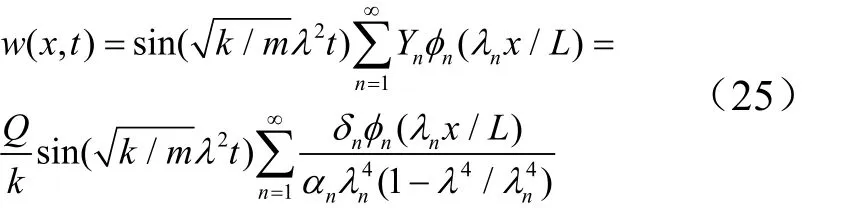
速度(,)v x t和加速度(,)a x t响应的表达式分别为:

弯矩(,)M x t可通过对位移(,)w x t两次微分得到:
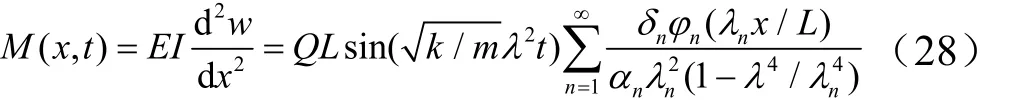
定义梁的静态位移为/Q k,考虑模态阻尼比ξ的动态位移放大系数βw(x,λ)为
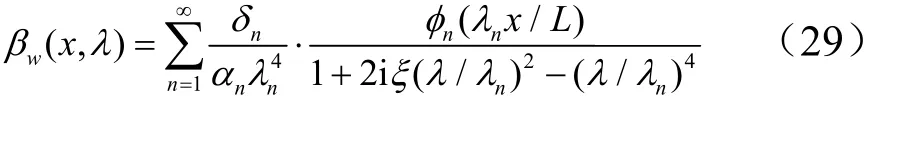
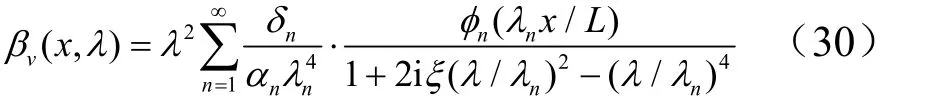
定义梁的准静态加速度为/Q m,加速度放大系数βa(x,λ)为
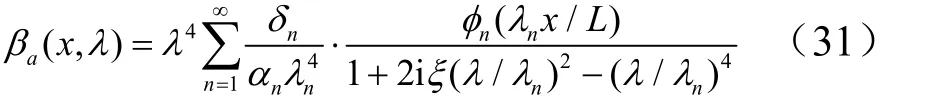
定义梁的静态弯矩为QL,动态弯矩放大系数βM(x,λ)为
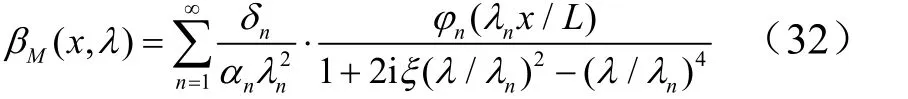
式(29)~(32)即为6种边界条件等直梁振动响应解析解的表达式。位移、速度和加速度的放大系数之间依次多一项无量纲因子(频率)2λ,因此其高频分量依次增大。而速度放大系数与弯矩放大系数的变化趋势相同,只是空间分布函数将振型改为振型曲率。
比较式(30)~(32)可知,在谐振频率处速度与动态弯矩的放大系数βv(x,λ)和 βM(x,λ)的变化规律相同。
图2给出了在阻尼比为ξ=0.01时4种响应参数动态放大系数的解析计算曲线,部分边界条件梁给出了两个截面的弯矩响应。由图2可以看出:加速度放大系数aβ的响应峰值变化相对平缓,高阶与低阶响应量级上没有差别;位移放大系数wβ的响应峰值下降较快;速度放大系数vβ响应峰值的变化介于两者之间,响应峰值随频率而下降。这3种参数响应曲线的交点位于一阶频率之前,曲线间距在交点后逐渐增大。根部弯矩放大系数Mβ的变化规律接近速度放大系数vβ,在响应峰值处基本一致,但在反共振谷的差别最大。在载荷分析中只考虑一阶弯矩载荷通常是不够的。等直梁无附加约束时的载荷分析阶次与速度相同,有附加约束时的载荷分析阶次与加速度相同[4]。
等直梁的动、静态响应存在内在联系。两者对于静平衡边界条件有一致性,可通过静态位移和静态截面弯矩对相应的动态响应结果进行确认。对于4种静平衡边界(两端简支、简支-固支、固支-自由、两端固支)梁,分别在中部和端部施加集中力、均布力和线性分布力,得到的动态位移和弯矩响应曲线(图2b、图2d与集中力对应)在频率趋于零时与静态响应数值一致,说明了振动响应推导结果的正确性。
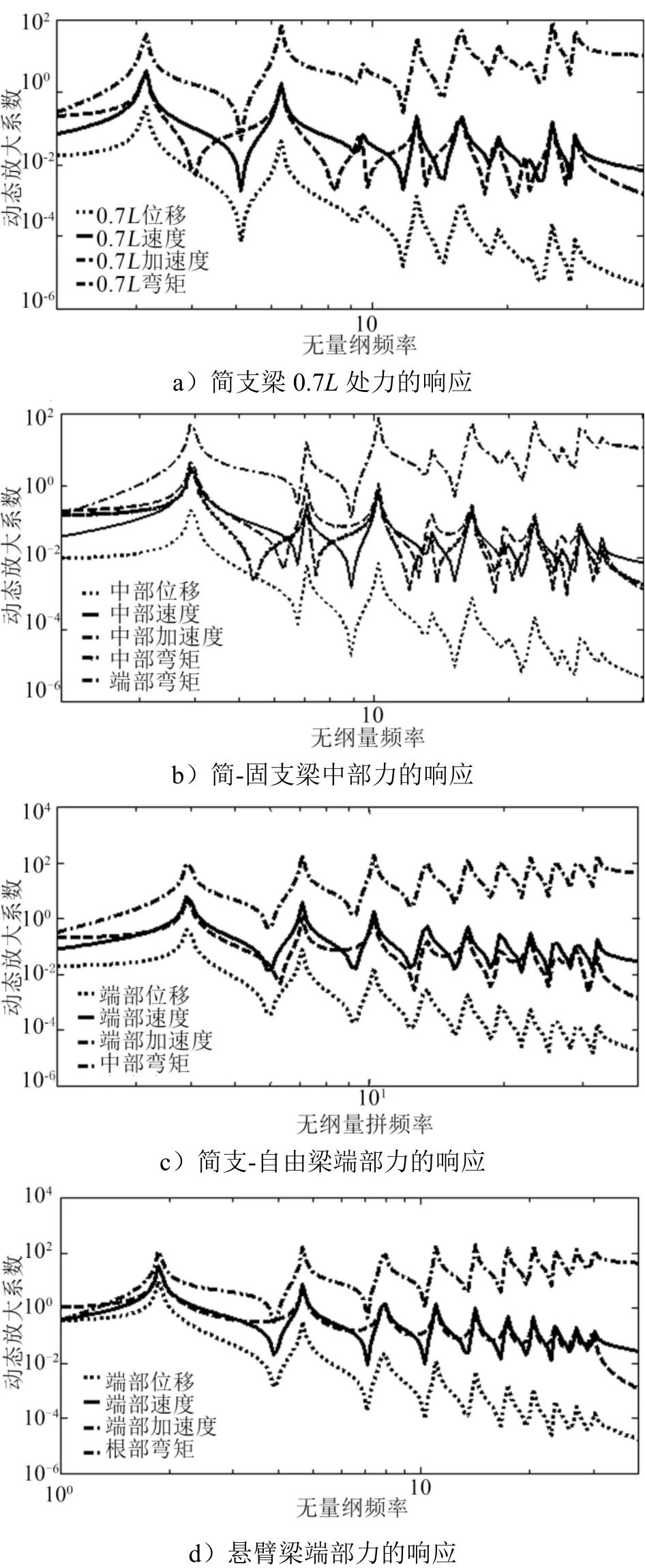
图2 六种边界条件等直梁的动态响应放大系数曲线 Fig.2 Dynamic Response Amplification Coefficient Curves for Uniform-section Straight Beam with Six Boundary Conditions
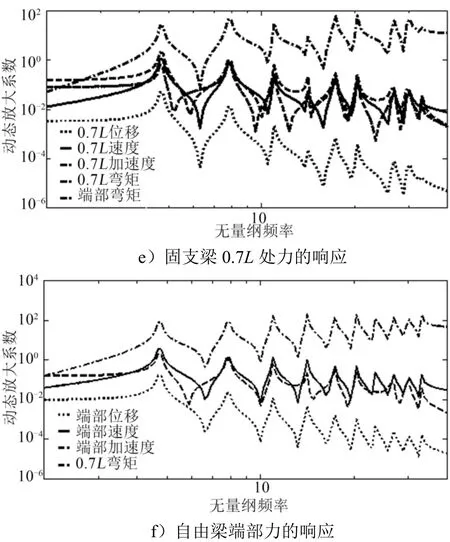
续图2
图2 只给出了部分集中力载荷形式和不同位置处的动态响应曲线。对于两端简支和两端固支梁,由于在中部施加集中力不能激励出偶数阶模态,只用于比较静、动态响应。
3 等直梁的有效质量
模态有效质量反映结构系统刚体模态和弹性模态的耦合作用,代表基础激励下各阶模态的动力学质量与响应,也是结构系统的一种动特性[9]。
等直梁的有效质量目前还没有解析表达式,其原因仍在于广义质量的解析表达式未得到。因此可在本文推导出的广义质量解析表达式的基础上,给出各种边界条件等直梁有效质量的解析表达式。第n阶有效质量的计算公式为[10,11]:

式中 mn为第1节中已得到的第n 阶 广 义 质量,mn= αnm; mrn为第n阶弹性模态与刚体平动模态的参与质量, mrn= mnr。第n阶参与质量的表达式为
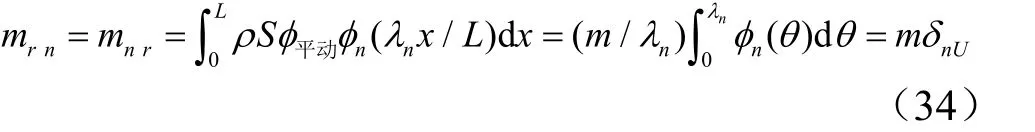
式中 δnU为第2节得到的均布力广义力 系数,由上述结果导出的有效质量 Mne为

式中 αne为有效质量系数,
由相应边界条件的广义质量系数和均布力广义力系数,得到了6种边界条件等直梁的有效质量系数(见表1)。各阶广义质量系数的数值基本恒定(分别为0.5和0.25),有效质量系数与均布力广义力的平方成正比。由于均布力的广义力随阶次增大而降低,因此有效质量系数收敛到零的速度更快,高阶有效质量更小,对振动响应和特性分析的影响也更小。从表1可以看出:
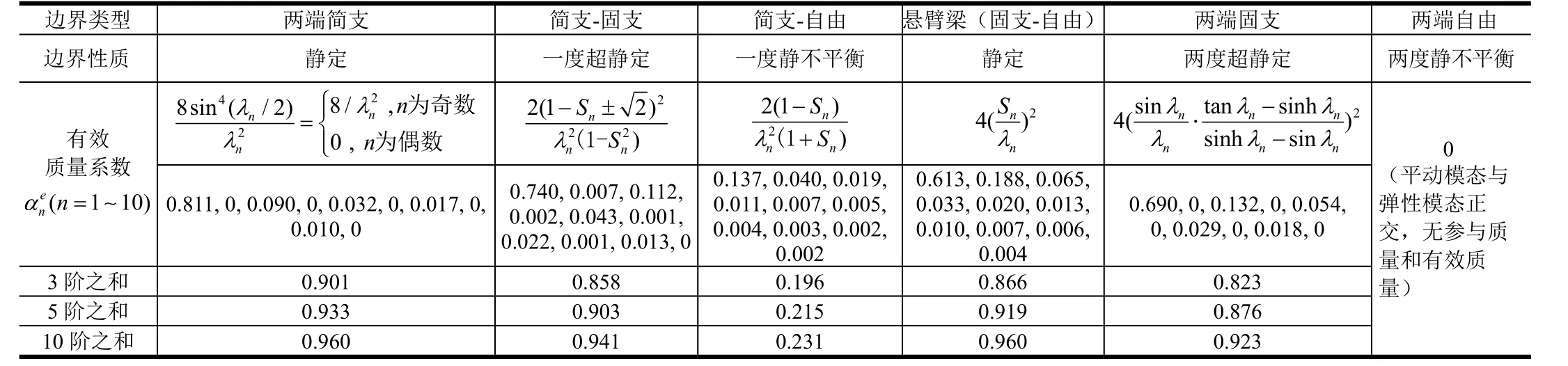
表1 六种边界等直梁的有效质量 Tab.1 Effective Masses for Uniform-section Straight Beam with Six Boundary Conditions
a)两端自由梁没有有效质量。简支-自由梁的第1阶有效质量仅为总质量的14%,前10阶有效质量之和仅为总质量的23%。两端简支梁的低阶有效质量最大。
b)对称边界条件梁的偶数阶有效质量均为零。由此可知自由边界条件结构(空中飞行的飞机、火箭和导弹)的有效质量为零,不能采用基础激励方式进行动响应试验,只能采用力激励方式;边界约束结构可采用基础激励方式研究其动响应。
4 结 论
本文基于特征变换方法和简洁振型函数,推导了两类边界条件等直梁(有、无简支边界)的广义质量解析解,获得了集中力、均布力和线性分布力激励下4种响应参数(位移、速度、加速度、动态弯矩)动态放大系数的解析解和曲线,并进一步得到了不同边界条件等直梁的有效质量,丰富了等直梁模态特性中广义质量、动态响应与有效质量解析解的研究成果。本文的主要研究成果如下:
a)3种含简支边界梁的各阶广义质量系数基本为0.5,另外3种不含简支边界梁的各阶广义质量系数均为0.25。
b)等直梁动态弯矩高频分量的衰减程度与速度同阶,低于位移的衰减程度。在载荷分析中只考虑一阶弯矩载荷通常是不够的,分析阶次应介于与速度与加速度分析阶次之间。
c)等直梁有效质量与均布力广义力系数相关,自由梁没有有效质量,简支梁的有效质量最大。对称边界条件梁的偶数阶有效质量均为零。
在等直梁未约束自由度的边界中,再增加有限约束后,也可获得其振动响应的解析解。例如,悬臂梁自由端带质量和弹簧约束的振动响应解析解已采用特征变换方法给出[4]。等直梁含自由或简支边界增加约束(各种质量和弹簧,包括转动惯量和角弹簧)后的振动响应解析解也可能获得,限制条件是附加约束数量不超过2个,可以在质量、转动惯量和线、角弹簧约束中选择。等直梁边界含3个及以上约束时的振动响应解析解能否得到,需要进行探索与研究。
对于与梁振动同为四阶导数运动方程的板振动问题,板结构增加了一维空间变量,为二维振动问题。对矩形板而言,在每个方向均包含2项三角函数与2项双曲函数,其振动响应通解为16项三角函数与双曲函数之积的和[5]。对于圆形板,又增加了贝塞尔函数,问题进一步复杂化。由于板结构振动问题特征方程和广义质量的表达式非常复杂,采用特征变换方法也不易求解该问题的振动响应解析解。板结构除四边简支时有振动响应解析解外,其它边界时均没有解析解。
