升力体飞行器全程弹道规划与制导研究进展

2023-01-12陈万春余文斌

导弹与航天运载技术 2022年6期

陈万春，于琦，杨劲，余文斌，杨良

（北京航空航天大学宇航学院，北京，102206）

0 引言

升力体飞行器是一种使用运载火箭助推，利用高升阻比特点在大气层内远距离高速滑翔的飞行器，与传统弹道导弹相比，具有机动范围广、飞行轨迹不确定性强、敌地面雷达探测距离短等优点，因而成为目前的研究热点问题。但是，升力体飞行器的飞行环境恶劣，力热约束强，其弹道规划和制导难度较大。

常规再入制导律首先需要规划再入走廊，在走廊内规划一条满足终端条件的参考轨迹[1]，但由于无法抑制由高升阻比引起的弱阻尼长周期弹道振荡，无法可靠导引以CAV为代表的高升阻比飞行器[2]。为了满足升力体飞行器起滑条件，对助推段与滑翔段交班误差要求严格，因此对助推段制导律提出了较高要求。为保证对敌方目标的有效打击，还需要满足反拦截约束。

陈万春教授及其团队在飞行动力学和制导领域工作20余年，在再入弹道优化、再入机动反拦截弹道规划与制导等方面完成多项研究，提出一系列适应再入任务的理论方法[3]。本文针对升力体飞行器弹道规划和制导中的难题，归纳总结研究团队近年取得的重要成果。

1 平稳机动滑翔弹道发现与机理研究

1.1 平稳机动滑翔弹道的发现

升力体飞行器滑翔段弹道具有长周期、弱阻尼振荡的特性，在弹道谷底时动压和热流容易超过力热约束且大幅增加控制难度。因此期望滑翔弹道是一条平滑无振荡的轨迹，即平稳机动滑翔弹道。在弹道规划时，发现通过改变初始状态，可以得到平稳机动滑翔弹道，如图1所示[4]。

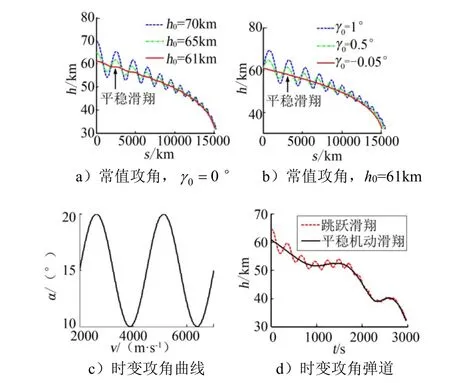
图1 不同初始状态下的滑翔弹道 Fig.1 Glide Trajectories with Different Initial States

1.2 弹道阻尼控制技术

如果只通过调整初始状态获得平稳滑翔弹道，则对初始状态有极高的精度要求，几乎无法实现。因此需要设计一种控制方法，使其在有初始状态偏差的情况下，弹道也能迅速收敛到平稳滑翔弹道，称之为弹道阻尼控制技术（Trajectory Damping Control Technique，TDCT）。

1.2.1 自然稳定滑翔弹道阻尼控制技术

自然稳定滑翔弹道阻尼控制技术的控制机理是将弹道倾角γ与平稳滑翔弹道倾角SGγ的偏差作为反馈项添加到基准攻角 bslα与基准倾侧角 bslσ中，以改变升力在铅垂方向上的分量来影响高度变化，最终使得弹道稳定在平稳滑翔弹道倾角附近[5,6]。利用弹道阻尼控制技术得到的指令攻角为αcmd= αbsl+ kγcosσbsl(γSG-γ)，指令倾侧角为σcmd= σbsl- kγsinσbsl(γSG- γ )α1。其中，kγ是反馈增益系数。弹道阻尼控制技术可以有效抑制自然稳定滑翔弹道的振荡，见图2。

图2 自然稳定滑翔弹道阻尼控制结果 Fig.2 Natural-stable Glide Trajectories with TDCT

1.2.2 自然不稳定滑翔弹道阻尼控制技术

针对自然不稳定弹道（如气动辅助变轨机动滑翔弹道），进一步引入高度H与平稳滑翔高度 SGH的偏差ΔH 作为反馈项，得到纵向升力系数的反馈其中 kf1， kf2与当前的高度、速度等飞行状态相关；ξ，ω根据极点配置法确定。当不采用弹道阻尼控制时，由于飞行速度大于第一宇宙速度，在科式力的作用下，飞行器高度迅速上升直至逃逸出大气层；当采用弹道阻尼控制时，飞行高度将稳定到平稳滑翔高度附近[7]，见图3。

图3 自然不稳定滑翔弹道阻尼控制结果 Fig.3 Natural-unstable Glide Trajectories with TDCT

1.3 平稳机动滑翔空间弹道解析解

利用弹道阻尼控制技术可以实现平稳机动滑翔，进而根据滑翔弹道动力学特性推导空间弹道解析解。研究解析解既可以避免大量的数值积分、实现快速弹道规划，对于滑翔弹道飞行机理研究也具有重要意义。

1.3.1 忽略地球自转的弹道解析解

通过对不考虑地球自转的再入运动模型进行适当的简化和线化[8]，得到了一个以纵向升阻比1/L D和横向升阻比2/L D为关键控制参数的线性时变系统，然后通过基于矩阵谱分解的LTV系统解析法解决了横程与航向角耦合的问题，获得了可以预测纵程xD、横程xC和广义航向角ψ~的三维空间再入弹道解析解。设E为当前能量，E0为初始能量，eR为地球半径，μ为引力常数，ki和 f (E0)与L1/D相关， F (E ,E0)与E和L2/D相关。则解析解的简化形式为

1.3.2 考虑地球自转的弹道解析解

为了补偿地球自转的影响，将由地球自转引起的惯性力与气动力组合为等效气动力，然后采用等效纵、

式中 XYCS-2= [xD,xC,,t]T，t为飞行时间；k =fk( L1D , L2D ,φ ,ψ ,ωe)为系数矩阵，与当前飞行状态、升阻比剖面和地球自转角速度ωe等相关。XYCS-2的详细表达式可见文献[9～10]。对于1万多公里的航程，该解析解的相对位置误差和飞行时间相对误差在3%以内。

1.3.3 大横程机动滑翔弹道解析解

在前期的解析解研究中，往往会忽略部分纵、横向耦合因素，假设飞行器保持在射面附近飞行。为提高大横程机动下解析解精度，需要充分考虑纵、横向运动耦合的影响，通过采用摄动法对非线性降阶动力学系统进行分阶处理，进而解析求解分阶子系统得到高精度的滑翔弹道解析解，表达形式为

图4中给出了7个不同射向的算例。升力体飞行器以约60°大小的倾侧角进行大横程机动时，最大横程接近4000 km。与弹道仿真结果相比，而无地球自转解析解（YCS-1）和考虑地球自转解析解（YCS-2）的横程最大相对误差超过45%，而大横程机动解析解（YCS-3）的精度大幅提升，横程相对误差小于1%。

图4 大横程机动解析解精度验证 Fig.4 Verification of Accuracy of the Analytical Solutions

1.3.4 星际航行返回滑翔再入解析解

以月球返回再入任务为例，飞行器再入速度可接近第二宇宙速度。对于高升阻比飞行器，可以通过在大气层内的长远距离滑行来消耗能量，与传统的二次再入弹道相比，这种再入方式峰值过载更小，更适合载人飞行任务。如图5所示，这种星际航行返回平稳滑翔再入弹道可分为拉起段和滑翔段，其中滑翔段又可分为3个阶段：自然不稳定滑翔、跨模态滑翔、自然稳定滑翔。

图5 星际航行返回平稳滑翔再入弹道示意 Fig.5 Sketch of the Special Re-entry Flight Scheme

在拉起段，升力将飞行器拉起至合适的高度以平稳切换至滑翔段；在自然不稳定滑翔阶段，飞行器以大于第一宇宙速度的速度大小飞行，纵向升力向下以平衡科氏力等作用；在跨模态滑翔阶段，飞行器在第一宇宙速度附近飞行，并且会经历升力方向从向下到向上的飞行模态变化；自然稳定滑翔段为常规的再入平稳滑翔阶段。针对上述各个阶段，目前均已推导了高精度的弹道解析解[7,10～13]。

2 滑翔段在线制导方法

高升阻比再入飞行器滑行距离远，横向机动能力强，具备禁飞区规避能力。本章主要介绍基于解析解的平稳滑翔在线弹道规划与制导方法：基于纵程解析解规划纵向升阻比剖面以满足能量管理需求，基于横程解析解规划倾侧反转点以规避禁飞区和满足终端横程约束。利用弹道阻尼控制技术抑制弹道振荡。

2.1 考虑多禁飞区的倾侧反转点解析迭代规划方案

本节介绍一种反转次数渐增的倾侧反转点解析迭代规划策略[9]：a）在首次规划中仅根据终端横程要求安排两次反转；b）逐个检测所有有效禁飞区约束满足情况：如果不满足某一个禁飞区约束，则进入c；如果满足，则保留原有反转点；c）基于解析解调整或增加倾侧反转点以规避禁飞区；d）重新规划后续的反转点以满足终端横程要求。当出现无法全部规避的情况时，优先规避威胁等级较高的禁飞区，并且在每处理完一个禁飞区约束之后就立即考虑终端横程约束规划后续的反转点，这样有利于防止轨迹为了规避禁飞区而偏离目标太远，从而导致最终无法抵达目标。

为了检验制导律的效果，这里提供2个算例：算例1中，飞行器需要面对16个半径为200 km的小型禁飞区；算例2中，飞行器需要规避3个半径为500～800 km不等的大型禁飞区。仿真结果如图6所示，飞行器成功规避所有禁飞区。

图6 绕禁飞区仿真结果 Fig.6 Simulation Results of No-fly Zone Avoidance

2.2 多飞行器协同再入弹道规划与制导

本节介绍基于时间解析解的多飞行器协同再入弹道规划与制导方法[10]。由于飞行时间和纵程都与纵向升阻比相关，这里将原本的常值纵向升阻比部分设计为线性纵向升阻比，从而增加一个关键剖面参数，并利用纵程解析解和时间解析解规划纵向升阻比剖面关键参数，从而在满足能量管理要求的同时控制飞行时间。

为展示协同制导律具备应对复杂情况的能力，图7给出了绕64个随机分布禁飞区（半径均为200 km）的协同再入飞行算例。飞行器V1～V3的初始高度为80 km，初始速度为7100 m/s，初始时间误差为30 s。终端误差如表1所示，从中可以看出协同再入制导律可以在保证终端精度的前提下很好地实现时间协同。

图7 绕64个随机分布禁飞区的再入协同飞行 Fig.7 Simulation Results of Coordinate Flight with 64 No-fly Zones

表1 协同制导终端误差 Tab.1 Terminal Error for Cooperative Guidance

2.3 基于解析解的横向大机动智能横程协同制导

为充分发挥横向机动能力，本节介绍一种基于强化学习的智能横程机动再入协同制导方法[14]。在纵向制导中，仍然采用基于纵程解析解的制导策略，以满足射程要求。在横向制导中，基于强化学习，寻找满足期望的最佳倾侧反转策略，以实现飞行时间协同，其算法结构如图8所示。

图8 DQN算法结构 Fig.8 Structure Diagram of DQN Algorithm

在训练好的智能体的基础上，开展仿真试验，结果如图9所示。将本节的制导算法称为“解析-智能制导”，2.2节的制导律称为“纯解析制导”。从图9中可以看出：针对不同再入任务，基于DQN的横向智能决策器摆脱了原来基于规则的横向制导逻辑约束，具备自主智能调节反转策略的能力和良好的任务适应性。通过较少的倾侧反转次数使得末段横向机动范围扩大约1000 km，令再入弹道横向设计具有更多的可能性。

图9 智能横程机动协同制导地面轨迹 Fig.9 Ground Tracks for Multi-vehicle Cooperative Attack

3 广义标控脱靶量在线最优制导方法

与零控脱靶量相比，标控脱靶量是指当飞行器采用任意已知控制律时，导弹和目标最终错过的距离。在此基础上，每一项终端约束的偏差均可视为广义标控脱靶量，可以大幅提升制导律的适应性。

3.1 助推段广义标控脱靶量制导律

3.1.1 助推段高精度弹道解析解

为快速计算广义标控脱靶量[15,16]，推导助推段高精度弹道解析解。根据泰勒展式，将弹道解析解分解为零控基准解、非零攻角增量解和非零侧滑角增量解，再使用摄动法分别求解。解析解的形式可表示为

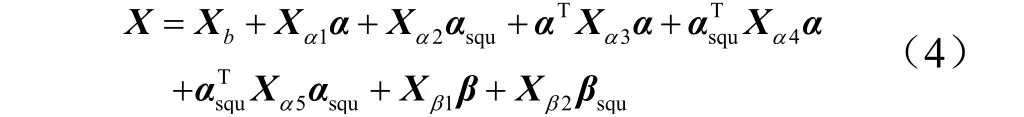
式中 X =[V ,γ, h,ψ]T；α和αsqu为插值节点处攻角和其平方组成的向量；β和squβ为插值节点处侧滑角和其平方组成的向量；1αX～5αX，1βX和 2βX为系数矩阵。

3.1.2 助推段多约束在线弹道规划方法

在进行标控攻角曲线设计时，需满足终端弹道倾角和高度约束。考虑如下性能泛函：

利用Gauss积分将性能泛函中的积分项进行离散，使用序列二次规划，可以求解插值节点处的攻角向量。最后，通过拉格朗日插值得到标称攻角。

为了满足终端速度及弹道偏角约束，设计如下标控侧滑角曲线：

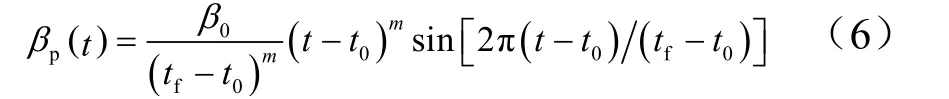
式中0β，m为待优化参数，可利用牛顿迭代法求解。

3.1.3 助推段多约束在线最优制导律

当飞行中存在扰动时，为了提升终端精度，还需设计助推段在线最优制导律。第1级程序转弯段可使用文献[17]中的方案。在制导段中，根据最优控制理论，可以推导得到最优制导律形式为

式中 Δ hf， Δγf， ΔVf， Δψf为广义标控脱靶量；Nh， Nγ，VN，Nψ为制导系数。

为了验证所提出的助推段制导律的效果，设终端弹道倾角为0°，终端高度可变，仿真结果如图10所示。当使用不同终端高度约束时，所得弹道簇与鹅头较为类似（见图10a），因此称之为鹅头弹道。

图10 助推段制导律仿真结果 Fig.10 Simulation Results of Guidance Law in Boost Phase

续图10

3.2 滑翔段线性伪谱广义标控脱靶量制导律

伪谱法因其不需要推导复杂的协态方程、对初值不敏感、具有指数收敛性质等优点，被广泛应用于最优控制问题的求解中。但伪谱法还存在收敛速率无理论证明、计算量大无法在线应用等难题。本节将介绍伪谱法收敛速率的理论证明方法和线性伪谱广义标控脱靶量制导方法，解决了上述难题。

3.2.1 伪谱法收敛性国际公开问题证明

自2006年起，Hager教授[18]开始对伪谱法收敛性证明问题进行研究，并将问题归结为状态、控制、协态和其最优解之差的范数需满足下式：

教师可结合上述问题与实际教学情况向学生提出：“三角形与直角坐标系具有哪些特殊的性质与特征？”等问题。其中教师的主要活动为结合实际问题提出科学的疑问，并让中等生对相应的问题进行解答。学生对问题进行回答期间若不完整，教师则应进行相应的补充与说明。其主要目的是让学生利用对以往数学知识的复习，使学生在解答这一函数动点问题期间可更好地想起以往学习的数学知识，并为其解题创造良好的条件。

进一步可归结为四类微分矩阵存在最大范数边界，由于证明难度太大，Hager教授于2015年将其作为数学公开问题发布。文献[18]中，通过推导欧式范数的解析表达式给出了Gauss配点和Radau配点下矩阵范数边界值的严格证明，攻克了这一国际计算数学公开问题，使该长达13年悬而未结的问题得到最终解决。

3.2.2 基于线性伪谱法滑翔段广义标控脱靶量在线最

优制导律

在本节中，将介绍线性伪谱模型预测控制方法（Linear Pseudospectral Model Predictive Control， LPMPC）[19,20]。其主要由4部分组成，分别是积分预测、拟线性化、线性伪谱求解和控制解析修正，流程如图11所示。该制导律的效果如图12所示。

图11 线性伪谱制导律流程 Fig.11 Flowchart of LPMPC

图12 线性伪谱制导律仿真结果 Fig.12 Simulation Results of LPMPC

为了检验该制导方法规避禁飞区的效果，开展如图13所示的仿真试验。10个升力体飞行器从不同的起点攻击3个目标，滑翔段中存在24个禁飞区约束。从图13中可以看出，10个飞行器均能规避全部禁飞区。

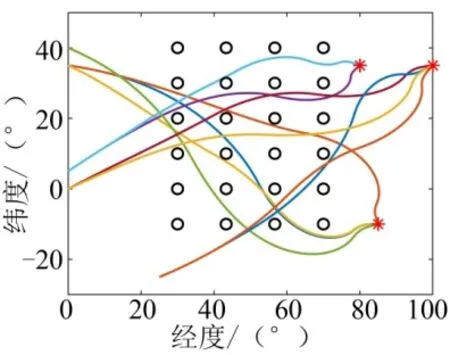
图13 绕多禁飞区线性伪谱制导律仿真结果 Fig.13 Simulation Results of LPMPC with Mutiple No-fly Zones

4 末段反拦截弹道规划方法

对于末段弹道而言，无法通过绕飞规避敌末段拦截系统。常用的反拦截机动设计方法有2种：选择合适的方向侧向绕飞；通过最优机动反拦截。

4.1 满足落角和落速约束的末段弹道规划

该方法是将空间弹道分解为纵平面弹道和水平面弹道，分别使用几何曲线独立设计得到的。当使用不同终端速度约束时，所得弹道簇与蝴蝶较为类似（见图14），因此称之为蝴蝶弹道。为了验证此类弹道的反拦截能力，使用PAC-3型拦截弹进行拦截仿真，拦截概率如表2所示。从表2中可以看出当落点偏角为-90°时，拦截概率可以缩小到0.1%。但受限于几何弹道的特点，当落点倾角确定后，落点偏角和落速相互耦合，无法独立调节。

图14 用于拦截仿真的蝴蝶弹道 Fig.14 Butterfly Trajectories for Intercept Simulation

续图14

表2 蝴蝶弹道对抗PAC-3拦截概率表 Tab.2 Penetration Probabilities of Butterfly Trajectories Against PAC-3

4.1.2 同时满足落角和落速约束的末段制导律

为了同时满足落角和落速约束，我们将制导律的形式分解为两部分[21]，即：acmd= aTSG+aspeed。其中，aTSG是弹道整形制导律生成的制导指令，其可以导引飞行器从预定方向命中目标，speeda是终点速度控制方案生成的机动指令，其控制飞行器做适当的横向机动，以调节终点速度大小。

为了导引飞行器从期望方向命中目标，这里采用文献[22]提出的弹道整形制导律，如式（9）所示：

式中 C1，C2为制导律系数，其余各变量的定义可见文献[22]。使用谱分解方法可以求得加速度指令的广义解析公式，并据此可得制导律系数稳定域，如图15所示，可以保证终端指令收敛到0。

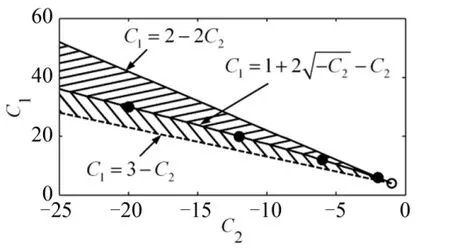
图15 弹道整形制导律系数稳定域 Fig.15 The Stability Domain of the Guidance Coefficients

终点速度控制方案产生加速度指令speeda方向在当地水平面内并垂直于包含速度矢量的纵平面，形式为

式中 kvf＞0，用于控制飞行器横向机动幅度，从而调节终点速度，可由割线法求解；0ψ为初始航向角为初始视线方位角。

为验证制导律的效果，给出了与传统弹道整形制导律对比的仿真结果，如图16所示，可以看出，所提出的制导律对终端速度和终端攻角的控制效果更好。

图16 弹道整形制导律仿真结果 Fig.16 Simulation Results of Trajectory-shaping Guidance

4.2 最优机动反拦截策略

4.2.1 多对象、多段、多约束反拦截弹道优化

为了反映较为复杂的攻防对抗场景，同时考虑进攻弹、拦截弹、打击目标3个对象，将攻防对抗时序分为弹目交战、拦截弹指令饱和、对地攻击等3个不同阶段，考虑热流、过载、动压、拦截弹动力学等约束，建立多对象、多段、多约束最优控制问题[23]。综合考虑反拦截性能、精确打击性能、控制平滑性能设计性能泛函，使用Radau伪谱法求解该最优控制问题，即可得到最优反拦截弹道。

为了验证最优机动弹道的优越性，与垂直S机动弹道进行对比，两种机动的控制曲线如图17所示。最优机动的拦截弹脱靶量为234.6 m，垂直S机动的拦截弹脱靶量为119.7 m，可见最优机动的反拦截效果更好。

图17 数值最优机动和程序机动对比 Fig.17 Comparison between Numberical Optimal Maneuver and Program Maneuver

4.2.2 基于脱靶量级数解的最优机动反拦截策略

由于Radau伪谱法计算量较大，不适合在线应用。利用伴随法，经过推导可得当目标阶跃机动时，使用比例导引律的拦截弹的脱靶量解析解为[24,25]

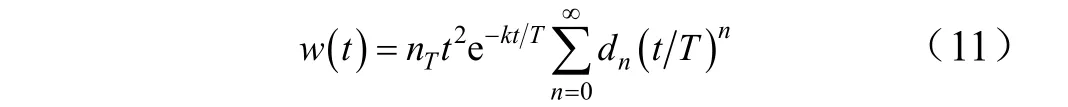
式中 k为衰减常数；n为需计算的项数；dn为系数。

最优机动的目的是使拦截弹脱靶量最大，因此最优反拦截控制律可表示为其中，tgo为剩余飞行时间。

为验证所提出最优制导律的性能，开展如图18所示的攻防对抗仿真。从图18中可以看出最优机动的反拦截效果明显。而当使用阶跃机动或蛇形机动等机动时，无法保证反拦截可靠性。

图18 基于脱靶量级数解的最优机动结果 Fig.18 Optimal Maneuver based on Power Series Solution of Miss Distance

综上：a）阶跃机动只有在弹目相对距离较短时可以产生与最优机动相同的效果，但机动时机的选择是关键。b）以蛇形机动、方波机动为代表的等周期机动在交战时间较长时，被拦截的机会也较多。c）数值最优机动和基于脱靶量级数解的最优机动都展现了最优机动是非等周期机动，只要制导时间足够长，最优机动的脱靶量可达阶跃机动数倍，但脱靶量解析解和机动变号时机是关键。