针对悬挂式水鸟的流噪声计算分析

张 玉，于大鹏，夏侯命胜，刘 松，孙海蛟

（1.大连理工大学船舶工程学院，辽宁 大连 116024；2.中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033；3.中国船舶及海洋工程设计研究院，上海 200011）

0 引 言

由于物探船作业的特殊性，必须考虑噪声信号对其工作的干扰。流噪声是众多干扰噪声源之一，是由船体或其他结构物与流体的相对运动及流体本身的无规律运动引起的流体内部应力和压力扰动在介质内传递产生的。部分物探组件距离检波器较近，其产生的流噪声可能会对物探船的探测作业造成干扰，因此有必要对其产生的流噪声进行预报。开展物探组件水动力噪声研究，有利于对地震波信号进行有效检测，对于开发海底油气资源而言具有重要意义［1］。流噪声研究起源于Lighthill的声类比理论［2］，该理论成功解决了自由空间发声的问题。CURLE将该理论推广到了存在固体边界的情况中，证明固体边界的存在等同于在固体表面均布偶极子声源，各偶极子声源的强度即为该点作用于流体上的压力，但其未解决运动固体与流体间的发声问题。WILLIAMS等对CURLE的研究成果进行推广，考虑运动固体边界对声场的作用，得到了FW-H方程，但该方程的求解难度较大，并未得到广泛应用。FARASSAT［3-4］对FW-H方程的积分形式进行了变换，并提出了求解方法。LANDAHL［5］对边界层湍流的结构和脉动压力进行了研究，发现爆裂模式产生了紧凑型偶极子和四极子噪声源，且其强度与湍流剪应力的产生有关。HARDIN［6］对低马赫数下湍流边界层的噪声进行了检验，结果表明，声源来自扰动雷诺正应力的超音速对流波数分量，具有明显的四极子性质；同时，对各种旋涡现象进行了分析，结果表明，声音主要在马蹄涡形成过程中产生，而黏性子层的爆裂可能是次级源。LAUCHLE［7］探索了刚性平板的声辐射问题，结果表明，声源主要集中在转捩区。LOCKARD［8］描述了FW-H方程在频域上的二维公式，通过假设所有声源的运动为亚音速直线运动，提出了一种高效且易于实现的方程形式，该方法能根据非线性近场流量预测远场噪声，用来指导和增强完整的三维计算。TEACHAJEDCADARUNGSRI［9］运用计算流体力学（Computational Fluid Dynamics，CFD）和Lighthill声类比理论研究了由二维圆柱层流涡脱落产生的声场，研究表明，由升力产生的偶极子源是影响总声密度起伏的主要因素；同时，运用电磁反馈控制方法减弱噪声，结果显示，无量纲声密度起伏减小了5个数量级。KIM等［10］对凸起表面的边界层进行了直接数值模拟，研究了表面纵向曲率对压力扰动和水动力噪声的影响，结果发现，表面偶极子在总声场中占主要地位，四极子对声场的贡献随着表面曲率半径的增大而增大。KALTENBACHER等［11］采用有限元与声类比相结合的方法计算湍流噪声，采用大涡模拟湍流流场，采用有限元方法求解Lighthill声类比方程的变分形式得到了声传播规律。通过比较同向旋转涡产生声场的数值解和相应的解析解，验证了此方法的可靠性；同时，对方柱模型湍流流场产生的流噪声进行全三维数值计算，并将所得结果与实测声压数据相比较，发现二者吻合较好，证明了该方法的适用性。

国内也已有很多学者对水动力噪声进行研究。杨德庆等［12］应用有限元软件NASTRN和声学有限元软件SYSNOISE，采用间接边界元方法对某船的近场和自噪声声学特性进行了计算，通过与试验结果相对比，证明了计算结果的可靠性。吕世金等［13］研究了水下航行体的流噪声，认为湍流边界层激励航行体壳体振动产生的水动力噪声在低频段起主要作用，边界层转捩区湍流猝发单极子声源对高频水动力噪声起主要作用。曾文德等［14］采用CFD和边界元方法计算了全附体潜艇的流噪声，流场计算结果表明，压力较大的区域在潜艇的艏部、指挥台围壳前部和鳍舵前部；同时，预测存在层流转捩的区域是声辐射较强的部位，声场计算结果验证了这一预测。

基于上述研究，本文采用声类比与CFD相结合的方法对物探组件的水动力噪声进行研究。首先，采用大涡模拟方法计算物探组件周围的流场分布情况，得到其表面脉动压力；其次，采用边界元方法将压力数据插值到边界元网格上作为声学边界条件，计算水动力噪声的辐射声场；最后，基于噪声计算结果分析物探组件水动力噪声对物探作业的影响。

1 计算理论

1.1 大涡模拟方法

大涡模拟方法根据一定的规则将湍流中的涡分为大涡和小涡2类，通过对非定常的N-S方程进行滤波处理得到大涡模拟的控制方程。滤波方程能过滤掉尺度小于滤波宽度的小涡，小涡对大涡的作用包含在大涡方程中，通过建立模型（亚格子尺度模型）模拟小涡的作用。

常用的滤波函数主要有盒式滤波函数、Fourier滤波函数和高斯滤波函数等3种，本文采用盒式滤波函数，经滤波处理之后，连续性方程和动量方程可分别表示为

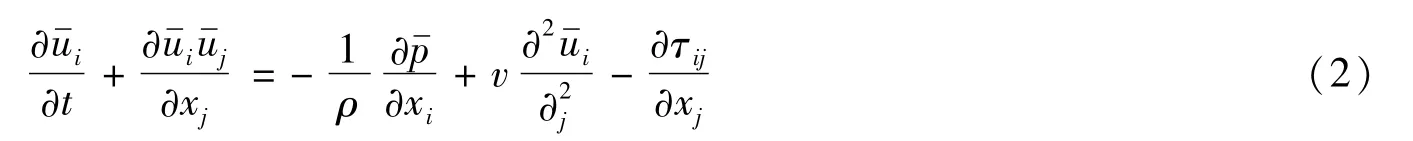
1.2 声类比理论

声类比理论首次将声场计算与流场计算相结合，在获得流场信息的基础上计算流噪声。该理论是由流体力学的基本方程（Navier-Stokes方程）推导而来的，其将声场分为近场和远场2种，近场为声源区，远场为辐射区，假设远场的流动对声场无影响。基于上述假设，可得到Lighthill声类比方程为

Tij的表达式为

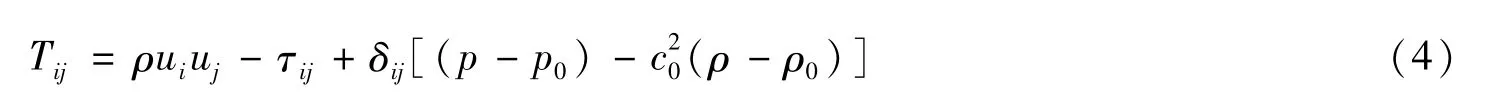
式（3）和式（4）中：ρ′=ρ-ρ0；p和ρ分别为当地流体的压强和密度；p0和ρ0分别为无穷远处流体的压强和密度；c0为无究远处流体的声速；Tij为Lighthill应力张量；δij为Kronecker符号；τij为黏性应力张量。

1.3 边界元方法求解流噪声

在边界元理论与Lighthill声类比理论结合过程中，仍要用到Helmholtz方程及其基本解的理论。对式（3）进行Fourier变换，令分别表示压力、密度、Lighthill应力张量在频域上的量，可得

式（5）中：k为波数，k=ω/c0。为方便表示，省去p′上方的冠标。

利用自由空间的格林函数得到声场中接收点r0处的声压为

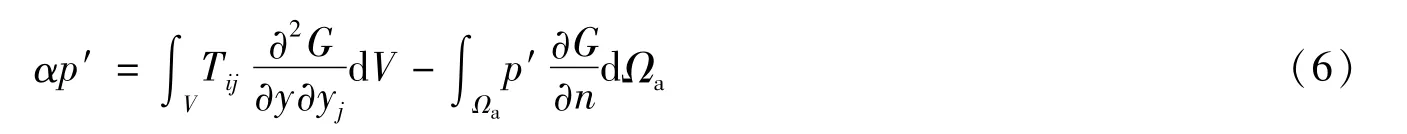
式（6）中：V为体积域；Ωa为固体边界；α为表面形函数，若接收点在固体表面取0.5，在求解域内取1；G为格林函数为声源点。

流噪声p′包含2部分，即水动力脉动压力ph和声学脉动压力pa，有

声压pa是要求解的项；水动力压力ph可通过流场非定常计算得到。

将积分区域分为2部分（V1和V2），对应的边界分别为Ω1和Ω2。V1为靠近接收点r0的体积，这里只受到声压pa的影响；V2为求解域内剩余部分的体积，这里受到ph和pa的影响。将式（7）代入式（6）中，利用Lighthill应力张量的近似公式Tij=ρ0uiuj可得到

对式（8）进行数值离散，以将积分式转化为线性方程组进行求解。于是，首先可将所求点的压力表示为

式（9）中：形函数Nei在节点i处取1，在其他位置取0；ne为单元Ωe上的节点数。

将式（9）中的局部形函数Nei扩展到整个表面，便得到整体形函数Ni，其在单元Ωe上取值为Nei，在其他位置取0，由此可得

将式（10）代入式（8）中，可得到

式（11）中：Q为Tij的体积积分，低马赫数下可忽略此项。

对边界上所有节点应用式（11）计算，可得到

式（12）就是采用边界元法求解流噪声的方程［15］，本文采用LMS Virtual.Lab的直接边界元法计算物探组件表面偶极子源辐射的声场。

2 物探组件水动力噪声计算

2.1 流场计算结果

水鸟产生的流噪声是干扰物探作业的噪声源之一，因此本文选取一种悬挂式水鸟作为研究对象，针对其水动力噪声进行计算分析。选取的水鸟的翼型为标准NACA651-012翼型，其型值见表1，其中X代表与翼厚度垂直的方向，Y代表翼厚度方向。该翼型属于层流翼型，其最大特点是将最大厚度点后移，达到减小翼型阻力的目的。

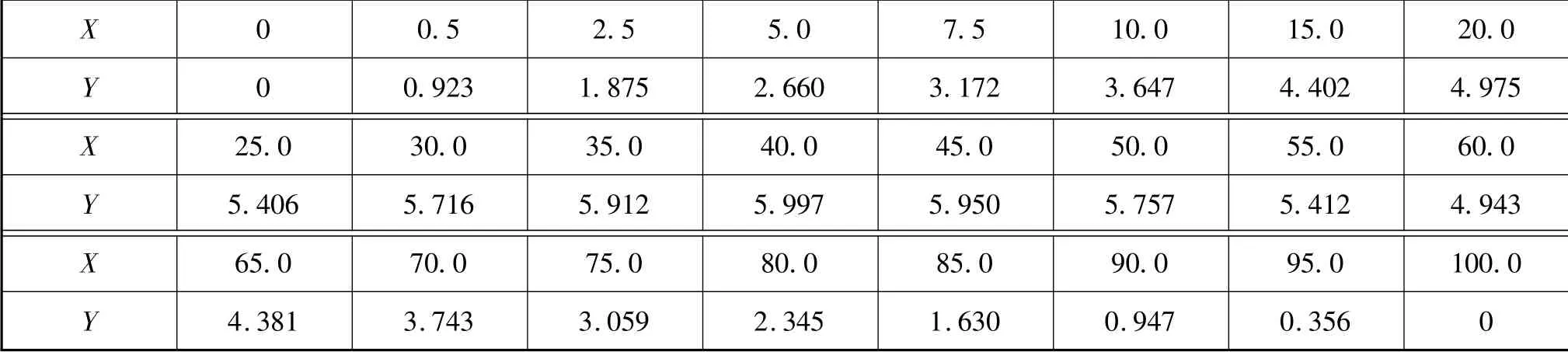
表1 NACA651-012翼型型值

根据表1建立水鸟物理模型（见图1），模型总长为3 m，翼展为0.8 m，两翼的剖面为NACA651-012翼型。采用专业流体力学分析软件Fluent进行计算，整个计算域为长方体，在水鸟的首部方向取1倍水鸟长度，在水鸟的尾部方向取2倍水鸟长度，计算域的横截面为长方形，边长取水鸟最大宽度的8倍。计算模型的雷诺数为1.3×106。图2为计算域网格，靠近水鸟表面的区域网格较为精细，以确保能捕捉流场的细节，网格数量约为171万个。计算中时间步长为5×10-5s，计算步数为2 000步。由采样定理可知，可分析的最大频率为5 000 Hz，转换到频域的分辨率为10 Hz。

图1 水鸟物理模型

图2 计算域网格

在计算过程中：计算域的左端面采用速度入口边界条件，速度入口给定的速度值为2.5 m/s，表示计算域左端面的法向流入速度为2.5 m/s；计算域的右端面距离模型尾部有2倍模型长度，可认为此处的流动已充分发展，因此采用自由流出边界条件；计算域的上、下、左、右等4个面采用对称面边界条件；模型的表面采用固壁边界条件。图3为水鸟表面压力云图。从图3中可看出，相比其他区域，水鸟首部和两翼附近的压力较大。流噪声主要是流场中的湍流脉动压力和不规则速度波动产生的，据此可预测首部和两翼对流噪声的贡献较大，在后续的流噪声计算中可证明该结论。

图3 水鸟表面压力云图

2.2 噪声计算结果

在流场计算中得到了水鸟壁面上的脉动压力数据，在采用边界元法计算水动力噪声时，将水动力脉动压力作为声源，提取水鸟表面的网格作为声学网格，采用LMS Virtual Lab的数据映射法将脉动压力由结构网格转移至声学网格。值得注意的是，由于采用Fluent计算得到的脉动压力是保存在网格中心的，在进行数据映射之前，需先将脉动压力数据由网格中心转移到网格节点上，再将其由结构网格映射至声学网格。计算时采用Maximum Distance映射法，假设源节点有4个，将Maximum Distance设置为300 mm，表示声学网格在以半径为300 mm的圆形区域内寻找n个结构网格上的节点作为该声学网格节点的源数据。若在该圆形区域内的节点多于n个节点，则取最近的n个节点作为目标节点的数据源；若在该圆形区域内的源节点不足n个，则取剩下的节点作为目标节点的数据源。在进行数据映射的同时，将压力数据由时域转换为频域，以频域的脉动压力作为边界条件进行声学计算。声学计算的边界元网格为二维面网格，满足最小波长内包含6个声学单元即可。另外，在LMS Virtual Lab中需将参考声压改为1×10-6Pa，通过建立面内压力为零的反对称平面模拟自由液面软边界，同时在水鸟中纵剖面所在平面上建立大小为60 m×30 m的声学场点面，以观察水动力噪声的空间分布情况。

在声学软件中计算完声场之后，即可观察场点的声压云图。图4为不同频率下垂直方向上的水动力噪声声压分布云图。

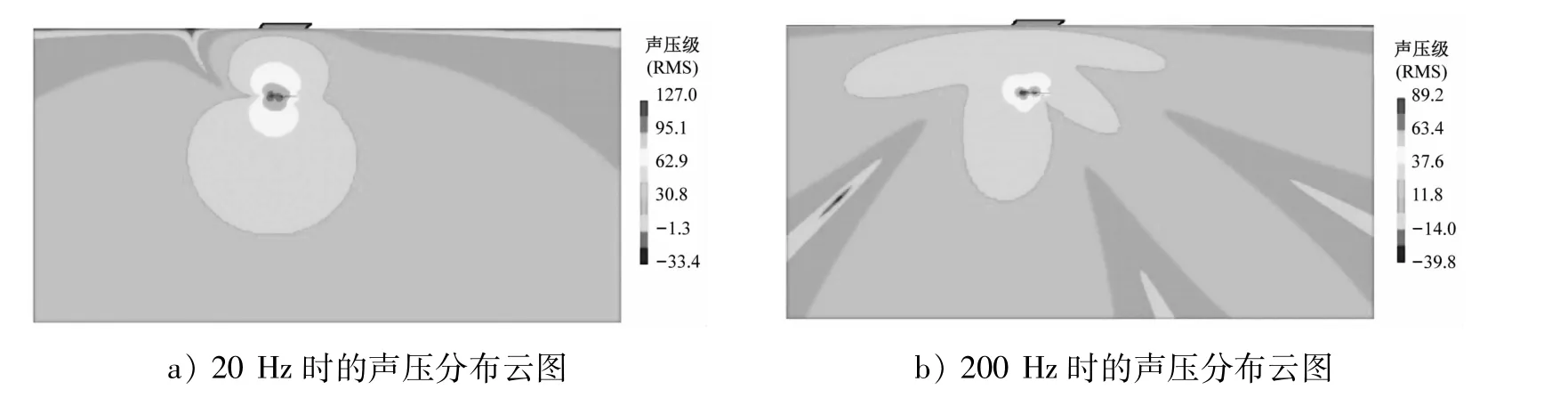
图4 不同频率下垂直方向上的水动力噪声声压分布云图

下面分别沿水鸟首尾方向（x方向）和垂直方向（z方向）选取若干个特征点，观察各特征点均方根声压随该点与壁面距离的变化，结果见表2。

表2 特征点均方根声压沿x方向变化

分别在x方向和z方向选取X2点和Z2点，绘制其流噪声声压曲线，见图5。下面观察x方向和z方向特征点均方根声压随特征点与壁面距离的变化规律，在20～2 000 Hz频段内特征点均方根声压随特征点与壁面距离的变化情况见图6。

图5 X2点和Z2点流噪声声压曲线

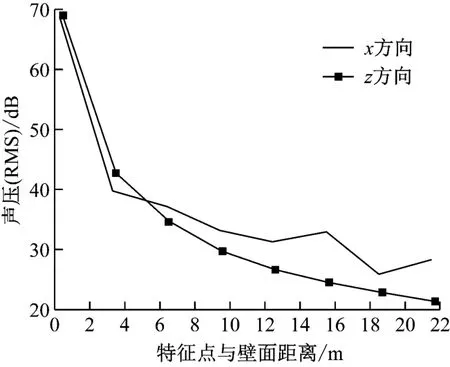
图6 x方向和z方向特征点均方根声压随特征点与壁面距离的变化曲线

从以上分析中可看出：

1）随着特征点与壁面距离的增加，声压逐渐衰减，水动力噪声在20～100 Hz频带内较大，最大声压可达127 dB；各频率下水鸟首部和两翼附近的声压值明显高于其他部位，验证了前面的预测。

2）x方向特征点均方根声压在近壁面区衰减较快；随着特征点与壁面距离的增加，声压衰减速率减慢；距离壁面0.3 m位置处的特征点的均方根声压约为70 dB。

3）z方向的特征点均方根声压的衰减规律与x方向基本相同；距离壁面0.5 m位置处的特征点的均方根声压约为70 dB。

4）随着特征点与壁面距离的增加，x方向个别点特征点的均方根声压略微增大，这可能是海面的反射作用导致声波在该位置叠加的结果。

3 结 语

本文分析了国内外流噪声的研究现状，基于Lighthill声类比理论，采用CFD与边界元相结合的方法研究了水鸟的流噪声，根据流场和噪声计算结果，可得到以下结论：

1）由于水鸟的结构相对复杂，其周围流场紊乱，导致水鸟不同截面位置的脉动压力分布不均匀，水鸟首部和两翼的流体脉动压力要大于其他部位，而壁面上的脉动压力是水动力噪声的成因，导致首部和两翼的噪声明显大于其他部位；

2）由垂直方向上的声压云图可知，由于流场的不规则性，导致脉动压力在结构表面分布不均匀，垂直方向的声压分布呈现不规律性；

3）由特征点声压曲线可知，水动力噪声的能量主要集中在10～300 Hz频段内，且噪声的峰值在70 dB左右；

4）由x方向和z方向的特征点均方根声压计算结果可知，在距离水鸟壁面0.5 m位置处，在20～2 000 Hz频段内水动力噪声均方根声压均不超过70 dB，而海洋环境噪声约为90 dB，在这种工况下基本上可认为水动力噪声已被环境噪声湮没。