超精密大行程麦克斯韦磁阻驱动器磁场建模与推力分析
2023-01-12赖磊捷朱利民
张 旭,赖磊捷,2,朱利民
(1.上海工程技术大学机械与汽车工程学院,上海 201620;2.上海市大型构件智能制造机器人技术协同创新中心,上海 201620;3.上海交通大学机械系统与振动国家重点实验室,上海 200240)
大行程超精密纳米定位是指能够在毫米级(≥1 mm)行程范围内实现纳米级(0.1~100 nm)分辨率或定位精度的一种技术[1-2]。目前广泛使用的压电驱动器具有纳米级精度,但其行程一般只有几十微米至几百微米[3]。另一种常见的驱动器——音圈电机也存在推力密度低的缺点,难以实现高频响快速跟踪任务[4]。近年来,荷兰埃因霍芬理工大学的Katalenic等和美国麻省理工学院的Lu等[5-6]先后研制了多种基于麦克斯韦力驱动的磁阻驱动器。区别于音圈电机的洛伦兹力驱动原理,麦克斯韦磁阻驱动器依靠磁阻最小原理产生变磁阻正应力,其大小与气隙处磁感应强度的平方成正比,且其励磁线圈集中绕制在定子上,故该类驱动器具有力密度大、惯量低、响应速度快、结构简单以及热负荷能力强等优点[7]。基于此,国内外学者如奥地利维也纳技术大学的Ito等和南京理工大学的Zhu等[8-9]设计了多种基于麦克斯韦磁阻驱动器的纳米定位平台。
为了对磁阻微定位平台进行精确的结构设计和控制,需要对超精密磁阻驱动器的磁场和推力进行准确建模和分析[10-14]。目前,采用磁路建模方法构建磁阻驱动器的等效磁路模型,并将其磁轭及气隙中的磁通量消耗等效为磁阻,同时考虑漏磁对其性能的影响,即能有效建立描述磁阻驱动器推力的解析模型[15-17]。但将传统磁路建模方法应用于毫米级大行程麦克斯韦磁阻驱动器时,由于涡流损耗和漏磁大幅增加、气隙区磁场分布不均匀且非线性强烈,使得利用单平面磁通测量结果计算得到的漏磁系数无法准确地描述该磁阻驱动器的漏磁特性,从而导致难以准确地建立推力解析模型[18-20]。
针对上述问题,笔者提出采用考虑加权漏磁系数的磁路建模方法对大行程麦克斯韦磁阻驱动器进行磁场和推力建模。首先,建立磁阻驱动器考虑漏磁前后的工作磁路,分析永磁偏置磁路的作用以及使用永磁偏置结构后仍具有非线性的原因,并利用电磁学基本原理及磁场的可叠加性建立磁阻驱动器的推力解析模型。然后,构建磁阻驱动器的三维模型,并利用有限元仿真软件进行三维磁场仿真分析,得到磁阻驱动器在永磁体及励磁线圈单独作用时的磁场分布情况及每个气隙处的加权漏磁系数,以准确描述其漏磁的大小及空间分布。最后,通过在磁阻驱动器磁路中增加漏磁磁阻来减小漏磁的影响,得到考虑加权漏磁系数的推力解析模型,并通过实验验证不同位置处推力随输入电流的变化情况,以验证解析模型的准确性。
1 大行程麦克斯韦磁阻驱动器的结构
图1所示为大行程麦克斯韦磁阻驱动器的整体结构,其由2个对称布置的驱动单元组成。该磁阻驱动器的定子由2组尺寸较大的C形磁轭、汝铁硼(Nd-Fe-B)永磁体和4组励磁线圈组成,其中永磁体提供偏置磁场,可改善磁阻驱动器的磁路,实现电磁驱动力的线性化;动子由与定子磁轭材料相同的2组硅钢片金属块相连而成;磁轭外侧安装的铝合金外壳可极大程度地减少磁轭周围的漏磁,相比于气隙(磁轭与动子之间部分,共4个气隙,记为g1、g2、g3和g4)中的漏磁,该部分漏磁可以忽略不计。本文所设计的磁阻驱动器的结构尺寸如表1所示。

图1 大行程麦克斯韦磁阻驱动器整体结构Fig.1 Overall structure of large stroke Maxwell reluctance actuator

表1 大行程麦克斯韦磁阻驱动器结构尺寸Table 1 Structure dimensions of large stroke Maxwell reluctance actuator
图2所示为大行程麦克斯韦磁阻驱动器的永磁偏置原理(因结构对称,仅显示单个驱动单元)。令动子处于中间位置时为坐标系各轴的初始位置,对应动子位置x=0 mm,此时左右的初始气隙宽度x0相等。由图2可知,该磁阻驱动器单个驱动单元的磁场主要由两部分组成:第1部分是由永磁体产生的偏置磁场;第2部分是施加电流I时励磁线圈产生的励磁磁场。由麦克斯韦力计算公式及磁场的可叠加性可知,当偏置磁场和励磁磁场叠加作用时,动子左右两侧的磁感应强度出现差异,即动子受到差动的麦克斯韦力,可产生与输入电流I呈良好线性关系的推力F。由此可见,推力F的大小与初始气隙宽度直接相关,随着初始气隙宽度的不断增大(本文取2.5 mm),气隙中的漏磁及磁场分布不均匀的程度增加,导致磁阻驱动器的推力密度(电机常数)随着初始气隙宽度的增大而减小,且呈现较为严重的非线性。因此,为了实现大行程麦克斯韦磁阻驱动器的精确结构设计和控制,需要对其磁场和推力进行准确建模与分析。

图2 大行程麦克斯韦磁阻驱动器的永磁偏置原理Fig.2 Permanent magnetic bias principle of large stroke Maxwell reluctance actuator
2 大行程麦克斯韦磁阻驱动器推力模型的建立
2.1 理想推力模型
为了得到不考虑漏磁的理想情况下大行程麦克斯韦磁阻驱动器的推力与气隙中磁感应强度的函数关系并建立相应的解析模型,分别建立其单个驱动单元的理想偏置磁路和理想励磁磁路,如图3所示。图3(a)中:Rpm为永磁体的磁阻;φp为流经永磁体磁阻Rpm的磁通;φpm为永磁体内部磁场强度等于0 T时所产生的总磁通;φ1为流入永磁体的总偏置磁通;φL、φ14和φR、φ11分别为流经左、右气隙磁阻R1和R4的磁通,φL=φ14,φR=φ11。图3(b)中:气隙磁阻R1与R4串联,故流经磁阻R1和R4的磁通φ21与φ24相等,且等于磁路中的总磁通φ2。

图3 理想偏置磁路和理想励磁磁路Fig.3 Ideal bias magnetic circuit and ideal excitation magnetic circuit
利用磁阻计算公式,可得气隙g1、g2、g3和g4处的磁阻R1、R2、R3、R4,分别为:

式中:μ0为真空磁导率,μ0=4π×10-7N/A2;S为垂直于磁通方向的磁轭及动子的横截面面积。
对于理想偏置磁路,利用电磁学理论计算可得:

式中:Br为永磁体剩磁;Lpm为永磁体高度。
联立磁阻计算式(1)和式(2),可得气隙g1、g4中的磁感应强度B11和B14,分别为:

对于理想励磁磁路,其总磁通φ2以及气隙g1、g4中的磁感应强度B21和B24分别为:

式中:N为单个励磁线圈匝数,本文取N=200;I为励磁电流。
联立式(3)和式(4),可得在不考虑漏磁的理想情况下磁阻驱动器单个驱动单元的推力Fid:

综上,在不考虑漏磁的理想情况下,整个大行程麦克斯韦磁阻驱动器的总推力Fia=2Fid。
2.2 考虑漏磁的推力模型
随着大行程麦克斯韦磁阻驱动器磁轭与动子间初始气隙宽度的增大,气隙中磁场分布不均匀程度上升且非线性更加强烈,导致气隙处的漏磁现象对磁阻驱动器推力的影响显著增加。因此,对于大行程麦克斯韦磁阻驱动器,理想情况下的推力模型误差较大,难以准确描述其推力F与输入电流I之间的关系。为了使推力解析模型更加精确,必须考虑实际工作过程中由磁阻驱动器材料固有特性以及气隙中磁场分布不均匀导致的漏磁现象。由麦克斯韦定律可知,由于漏磁通未穿过动子横截面,因此无法参与麦克斯韦力的产生,减小了该磁阻驱动器的推力。为了清晰地描述偏置磁路和励磁磁路中的漏磁情况,分别在2种磁路中加入漏磁磁阻,并对添加漏磁磁阻后的磁路进行进一步分析,以建立考虑漏磁的推力解析模型。
图4所示分别为考虑漏磁的偏置磁路和励磁磁路。图中:RL11、RL14分别为气隙g1、g4中的偏置漏磁磁阻,φL11、φL14为流经相应偏置漏磁磁阻的漏磁磁通;RL21、RL24分别为气隙g1、g4中的励磁漏磁磁阻,φL21、φL24为流经相应励磁漏磁磁阻的漏磁磁通;其余参数与图3同。定义偏置磁路中流入永磁体的磁通φ1与流入气隙磁阻R1、R4的磁通φ11、φ14的比值为偏置漏磁系数k1j(j=1,4);励磁磁路中总磁通φ2与流入气隙磁阻R1、R4的磁通φ21、φ24的比值为励磁漏磁系数k2j(j=1,4)。则偏置漏磁系数k1j和励磁漏磁系数k2j为:


图4 考虑漏磁的偏置磁路和励磁磁路Fig.4 Bias magnetic circuit and excitation magnetic circuit considering magnetic flux leakage
对于图4(a)所示的考虑漏磁的偏置磁路,由电磁学理论可知,气隙磁阻与漏磁磁阻并联,且均与永磁体并联,则气隙g1和气隙g4处磁动势相等,可得:
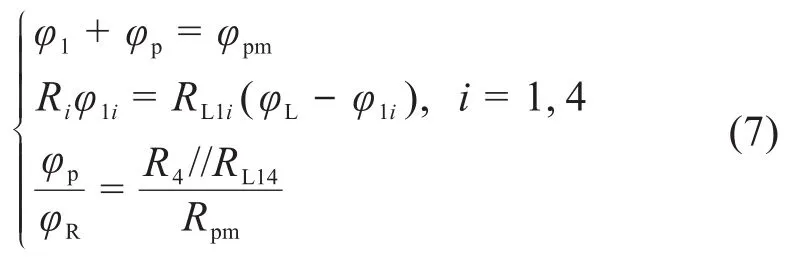
联立式(1)、式(2)、式(6)和式(7),得到偏置磁路中气隙g1、g4处的磁感应强度B11、B14:

对于图4(b)所示的考虑漏磁的励磁磁路,由安培环路定律和磁路的欧姆定律可知:

式中:i=1,4。
联立式(1)和式(9),可得:
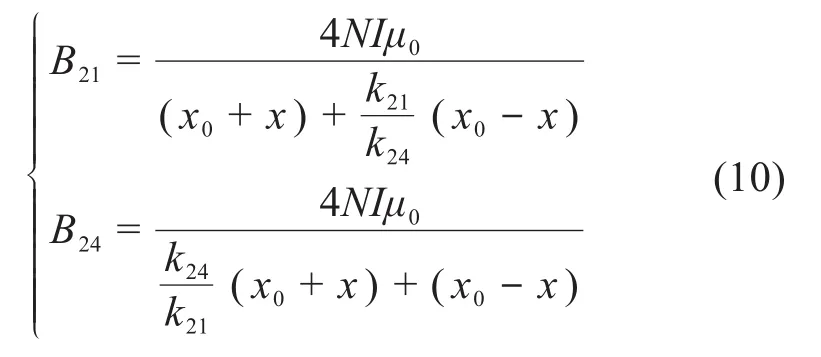
由电磁学理论以及磁场的可叠加性可知,当考虑漏磁的偏置磁路与励磁磁路同时作用时,气隙g1、g4处的磁感应强度为:
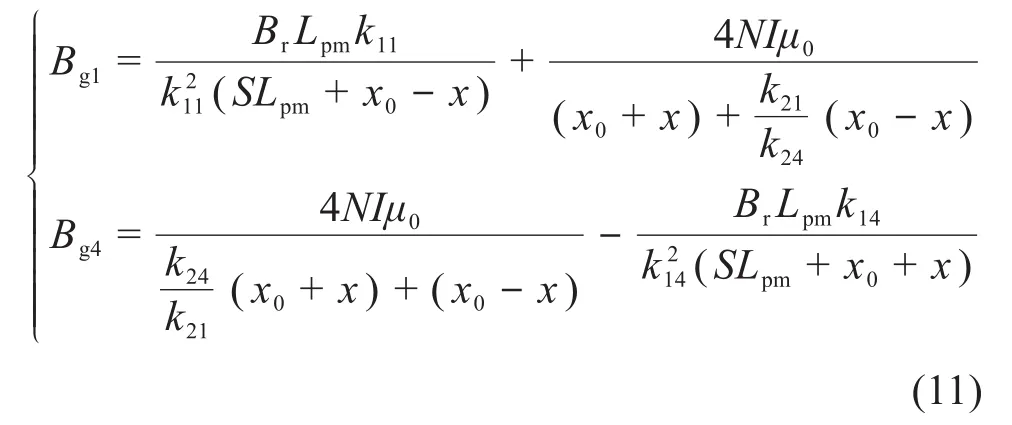
联立式(5)和式(11),可得考虑漏磁的大行程麦克斯韦磁阻驱动器的推力Fa:

2.3 漏磁系数仿真计算
虽然上文所建立的考虑漏磁的推力解析模型可揭示大行程麦克斯韦磁阻驱动器采用永磁偏置磁路后仍具有非线性的原因,但在实际建模过程中,与动子位置x相关的漏磁系数kij(i=1,2;j=1,4)的值很难通过理论分析或实验方法获得。此外,随着初始气隙宽度x0的增大,基于单平面磁通的传统漏磁系数计算方法的误差较大,无法准确描述大行程麦克斯韦磁阻驱动器的漏磁情况。为了获得更加准确的漏磁系数,提高推力解析模型的精确性,利用有限元仿真软件ANSYS中的Maxwell 3D模块对大行程麦克斯韦磁阻驱动器的三维磁场进行分析,以获得与定子位置相关的漏磁系数,仿真所用的具体参数如表2所示。
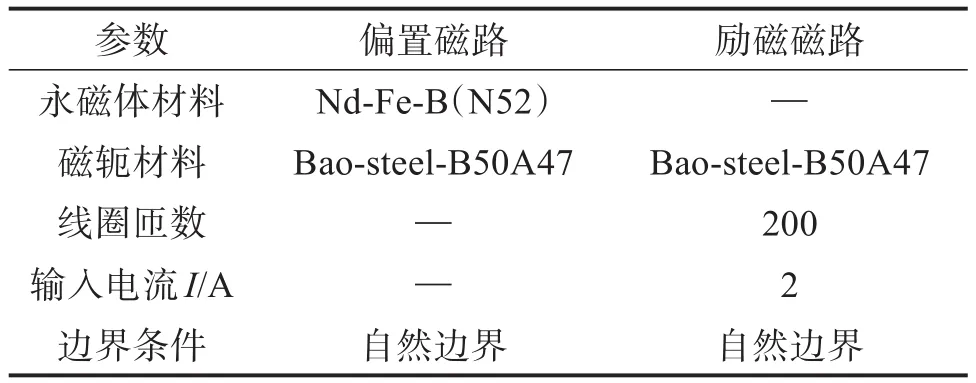
表2 大行程麦克斯韦磁阻驱动器三维磁场仿真参数Table 2 Three-dimensional magnetic field simulation parameters of large stroke Maxwell reluctance actuator
图5所示为大行程麦克斯韦磁阻驱动器动子位置x=0 mm时,其励磁磁场和偏置磁场的磁感应强度分布情况。由图5可知,对于偏置磁路,当动子处于初始位置时,磁轭及气隙中的磁感应强度以永磁体为中心线对称分布,此时气隙g1、g4中的磁感应强度分布情况基本相同。对于励磁磁场,当动子处于初始位置时,其分布规律与偏置磁场大致相同,磁通基本沿磁轭流动,且动子两侧气隙中的磁感应强度相等。另外,从图中还可以看出,铝合金外壳的存在较好地抑制了磁轭周围的漏磁现象。
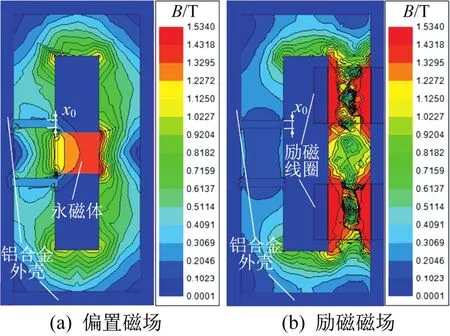
图5 偏置磁场和励磁磁场的磁感应强度分布云图Fig.5 Nephogram of magnetic induction intensity distribution of bias magnetic field and excitation magnetic field
进一步对励磁磁场和偏置磁场叠加作用时大行程麦克斯韦磁阻驱动器的磁感应强度分布情况进行分析,结果如图6所示。由于偏置磁场的磁感应强度在磁轭中呈对称分布,当偏置磁场与励磁磁场叠加后,磁轭及气隙中一侧的磁感应强度减弱,另一侧的磁感应强度增强,使得动子两侧受到差动的麦克斯韦力。通过合理的参数配置,可从理论上消除该磁阻驱动器的非线性。然而,随着磁阻驱动器运动范围的增大,气隙中漏磁现象的影响逐渐变大,导致其推力与输入电流之间仍呈非线性关系。
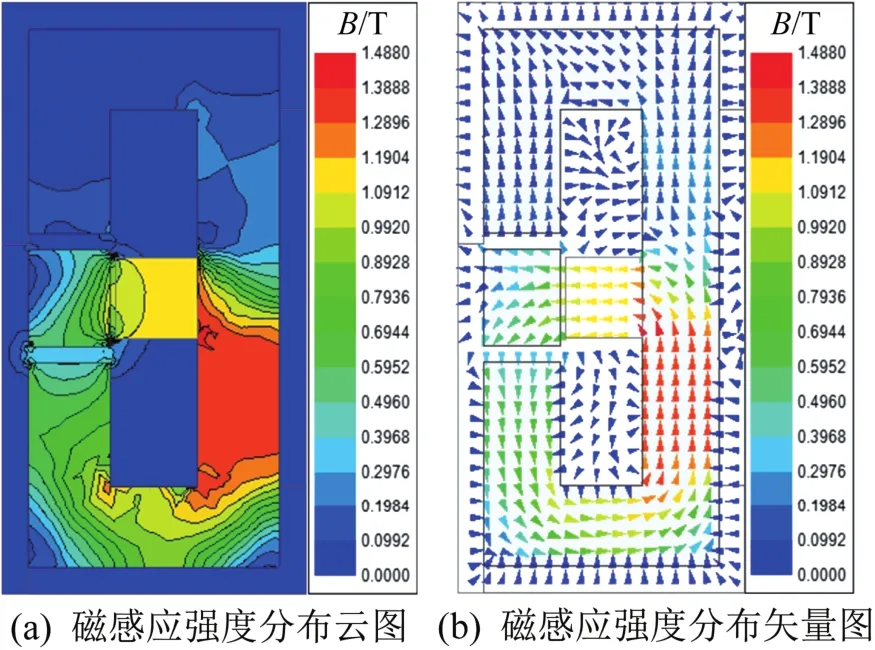
图6 励磁磁场和偏置磁场叠加时的磁感应强度分布情况Fig.6 Magnetic induction intensity distribution with superposition of bias magnetic field and excitation magnetic field
此外,不同于常规麦克斯韦磁阻驱动器微米级的运动范围,当初始气隙宽度x0=2~3 mm时,直接使用传统单平面磁通计算方法获得的漏磁系数会影响大行程麦克斯韦磁阻驱动器推力解析模型的精度。因此,在大行程麦克斯韦磁阻驱动器建模过程中,需要对流经大气隙中不同位置平面上的磁通进行加权处理,以提高漏磁系数对其漏磁分布的描述精度。
为了获得加权漏磁系数,首先,分别令气隙g4中动子的左侧横截面以及气隙g1中磁轭的左侧横截面为中心平面,利用方差为0.5 mm的高斯曲线选取气隙g4及g1中的磁通测量平面Si4,p和Si1,p(i=1,2;p=1,2,3,4,5);然后,利用有限元仿真软件中的后处理计算功能对永磁体横截面Sp、磁轭横截面Sc以及气隙g4和g1中横截面Si4,p和Si1,p(i=1,2;p=1,2,3,4,5)上的磁感应强度进行积分计算,得到流经相应横截面的磁通φ1、φ2、φi4,p和φi1,p(i=1,2;p=1,2,3,4,5)。基于横截面Si4,p和Si1,p(i=1,2;p=1,2,3,4,5)与中心平面之间的距离,计算高斯曲线中所对应的概率λi4,p和λi1,p(i=1,2;p=1,2,3,4,5)并将其作为权重来计算气隙g4和g1中的加权磁通:

最终计算得到的大行程麦克斯韦磁阻驱动器偏置磁路及励磁磁路中的磁通如图7所示,图中正负号代表磁通的流动方向。由图7可知,在动子从x=-2.5 mm移动到x=2.5 mm的过程中,气隙g4中的工作磁通逐渐减小,漏磁通逐渐增加,而气隙g1中的工作磁通随气隙宽度的减小而逐渐增大。由此可知,在该磁阻驱动器的整个行程中,其磁通变化呈非线性,当行程小于0.5 mm时,加权磁通与由单平面测量方法求得的磁通基本保持一致,此时由加权计算方法和单平面测量方法求得的漏磁系数并无明显区别。随着磁阻驱动器行程变大,当动子位置x=2~2.5 mm时,气隙中的磁通变化剧烈,此时加权漏磁磁通与加权励磁磁通均与由单平面测量方法求得的磁通有较大差异,且均小于由单平面测量方法求得的磁通。

图7 偏置磁路和励磁磁路中的磁通Fig.7 Magnetic flux in bias magnetic circuit and excitation magnetic circuit
联立式(6)和式(13),计算得到偏置磁路和励磁磁路中的加权漏磁系数,如图8所示。由图8(a)可知,由于偏置磁路中仅有永磁体作为磁力源,磁路对称,当动子由x=-2.5 mm运动至x=2.5 mm时,气隙g1中磁通的变化情况与反向运动时气隙g4中磁通的变化情况保持一致。因此,加权漏磁系数在整个行程范围内对称,且大于由单平面测量方法求得的漏磁系数。对于励磁磁路,当励磁线圈中励磁电流方向变化时,磁轭中的磁通方向随之变化;当动子距离初始位置较远时,该磁路中磁通的变化趋势逐渐平缓。由图8(b)可知,在该磁阻驱动器的整个行程内,由加权计算方法得到的磁通均大于由单平面测量方法求得的磁通。

图8 偏置磁路和励磁磁路中的漏磁系数Fig.8 Magnetic flux leakage coefficient in bias magnetic circuit and excitation magnetic circuit
综上所述,考虑加权漏磁系数的大行程麦克斯韦磁阻驱动器的推力解析模型为:

3 大行程麦克斯韦磁阻驱动器推力解析模型仿真与实验验证
为验证所构建的考虑加权漏磁系数的大行程麦克斯韦磁阻驱动器推力解析模型的准确性,利用有限元仿真软件ANSYS中的Maxwell 3D模块开展仿真分析并进行对比。在有限元仿真软件中,基于大行程麦克斯韦磁阻驱动器三维模型,按照表2进行仿真参数设置,求解当动子位置x=-1.5,-0.3,0.8,1.5,1.9 mm时,输入电流I在2 s内从0A上升至2 A所产生的推力Ffea,解析模型计算结果与有限元仿真结果的对比以及两者的均方根误差如图9及图10所示。

图9 优化前后解析模型计算推力与仿真推力的对比Fig.9 Comparison between calculated thrust of analytical model before and after optimization and simulated thrust
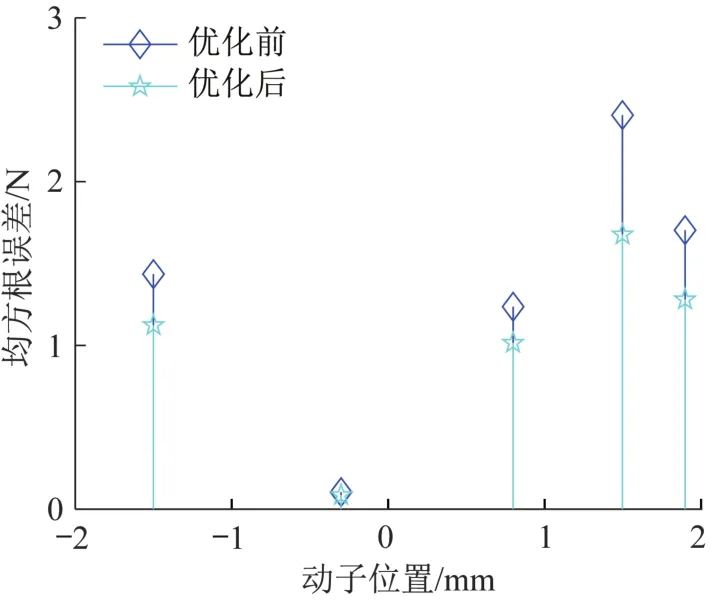
图10 优化前后解析模型计算推力与仿真推力的均方根误差Fig.10 Root mean square error between calculated thrust of analytical model before and after optimization and simulated thrust
由图9和图10可知,大行程麦克斯韦磁阻驱动器推力的解析计算结果与仿真结果基本一致,且推力与输入电流保持较好的线性关系;优化后解析模型的计算结果与仿真结果的均方根误差小于2.5 N,仅为最大推力的3.5%,且随着动子与中心位置之间距离的增大,解析计算结果与仿真结果之间的误差逐渐增大。即:当动子距离初始位置较远时,该磁阻驱动器气隙中的漏磁现象对推力的影响更为明显。由图9和图10还可以看出,优化后解析模型计算推力小于优化前的,且与仿真结果的均方根误差更小,可以更好地描述该磁阻驱动器动子处于不同位置时推力与输入电流的关系。
为了测量大行程麦克斯韦磁阻驱动器的实际推力和进一步验证解析模型的准确性,搭建了基于LabVIEW的推力测试系统,如图11所示。其中CH808线性放大器将PCI-6221数据采集卡的输出电压(-10~10 V)线性转换为磁阻驱动器的输入电流(-8~8A);推力由MZLG力传感器(量程为±50 kg)测量,并通过变送器实现-10~10 V的模拟量输出,并由数据采集卡进行实时采集。

图11 大行程麦克斯韦磁阻驱动器推力测试系统Fig.11 Thrust test system of large stroke Maxwell reluctance actuator
在推力测试实验中,输入电流I、动子位置x均与仿真时设定一致,并利用力传感器对动子位置x=-1.5,-0.3,0.8,1.5,1.9 mm时大行程麦克斯韦磁阻驱动器的推力进行测量,优化前后解析模型计算推力与实测推力的对比如图12所示。
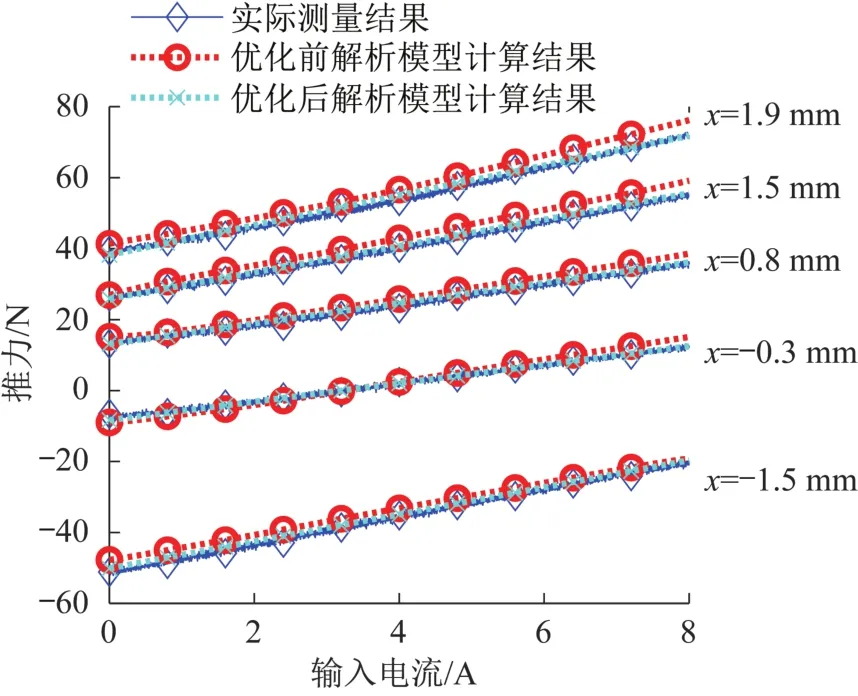
图12 优化前后解析模型计算推力与实测推力的对比Fig.12 Comparison between calculated thrust of analytical model before and after optimization and measured thrust
为了验证优化前后解析模型的精度,基于优化前后解析模型计算推力和实测推力计算均方根误差,结果如图13所示。由图13可知,对于大行程麦克斯韦磁阻驱动器,优化前解析模型计算推力与实测推力的均方根误差在大部分情况下均大于1.7 N,优化后解析模型计算推力与实测推力的均方根误差明显下降,均小于0.6 N。由此可见,加权漏磁系数的使用,有效地提高了推力解析模型的精度。

图13 优化前后解析模型计算推力与实测推力的均方根误差Fig.13 Root mean square error between calculated thrust of analytical model before and after optimization and measured thrust
4 结论
本文利用考虑综合高斯函数的加权漏磁系数的磁路建模方法,改进了大行程麦克斯韦磁阻驱动器漏磁系数的计算方式,得到了可准确描述其推力与输入电流函数关系的解析模型。首先,对大行程麦克斯韦磁阻驱动器的理想磁路进行了分析并与考虑漏磁的磁路进行对比,探究了漏磁现象对推力的影响,验证了建模时考虑漏磁的必要性。然后,通过对大行程麦克斯韦磁阻驱动器三维磁场的仿真,得到了其偏置磁场和励磁磁场单独作用时的磁场分布以及漏磁情况,并通过计算得到了基于高斯曲线的加权漏磁系数。最后,搭建了大行程麦克斯韦磁阻驱动器的推力测试系统,并将仿真推力和实测推力与优化前后解析模型计算推力进行了对比。结果表明,优化后解析模型计算推力与实测推力之间的均方根误差仅为优化前解析模型的11.1%,且与实测推力的均方根误差小于0.6 N,有效提升了解析模型的精度。
