“反比例函数”教学及反思
2023-01-11吉林师范大学郑凤丽
⦿吉林师范大学 郑凤丽
1 引言
教学是师生之间的一场相互成就,教学效果的达成,不仅要靠教师口口相传,还要依靠师生之间的有效互动,两者相辅相成,缺一不可.教学不是最终目的,让学生在头脑中建立起自己的认知结构,能将所学知识举一反三,在实际生活中遇到问题,能够用数学知识予以解决,这些才是教学的真正目的.因此,在研究教学时,不仅要研究课堂中的实际教学过程,还要研究学生在学习知识时的状态及特点.这样的教学研究才不会对象单一、有失偏颇,研究出来的结果才具有参考价值,得出的教学启示才有意义.
2 教学分析
函数的学习是前后连贯,一脉相承的.学生在学习反比例函数之前,对一次函数的研究已有大体思路.因此,在学习反比例函数时,学生将之前所学习到的有关函数的知识纵向迁移到反比例函数这个新知上,就会游刃有余,利用知识迁移的方法,学生对反比例函数也不会感觉陌生[1],学习这部分内容时就不会那么吃力.
在初中阶段,反比例函数是要求学生掌握的一个极其重要的函数内容.日常生活中有许多与反比例函数有关的问题,可以用数学知识来描述.因此,运用大家耳熟能详的路程问题,通过判定速度与行驶路程所用的时间,来引出所要学习的新知识点——反比例函数.
3 教学实录
3.1 创设情境,提出问题
师:同学们,我们已经学习了反比例函数的概念,根据之前学习一次函数的经验,想一想,对于反比例函数,我们还需要研究什么?
生:图象.

生:列表、描点、连线.
师:解析式里面有参数k,列表方便吗?
生:不方便.
师:那应该怎么做呢?
生:可以对k取特殊值试一试.
师:非常好!那么我们取k=6.
设计意图:展示研究数学问题的常见方法:从特殊到一般.
3.2 科学验证 解决问题
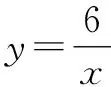
师:通过刚才的引入,我们首先应该列表,那么列表的时侯x可以取哪些值呢?
生:应该考虑自变量的取值范围,x≠0.
师:是否需要把所有x的值列举出来呢?
生:不需要.
师:那应该如何取值呢?(学生分小组自行讨论.)
生:为了方便描点与计算,可以取x<0和x>0的整数值.
师:请大家计算对应的y值应该为多少?(学生思考.请几位学生在黑板上填写答案,见表1.)

表1
师:列出表格,下一步需要做什么?
生:描点.(学生描点,教师利用多媒体课件展示描点的动态过程,如图1所示.)

图1
设计意图:让学生自己描点,并观察点的位置,以此培养学生独立作图的能力.
师:用平滑的曲线将描出的点连接起来,如图2,图象与坐标轴会有交点吗?(学生讨论)
生:根据反比例函数解析式可知,图象应该与x轴无交点.
师:同学们回答得非常好!虽然函数图象比解析式更直观,但如果要进一步了解函教图象,还得借助函数解析式.同理,图象和y轴有交点吗?
生:也没有交点.
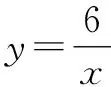
生:两支.
设计意图:让学生认知上得到发展,提高数形结合意识和数学思维能力.

生:图象分布在第二、四象限.
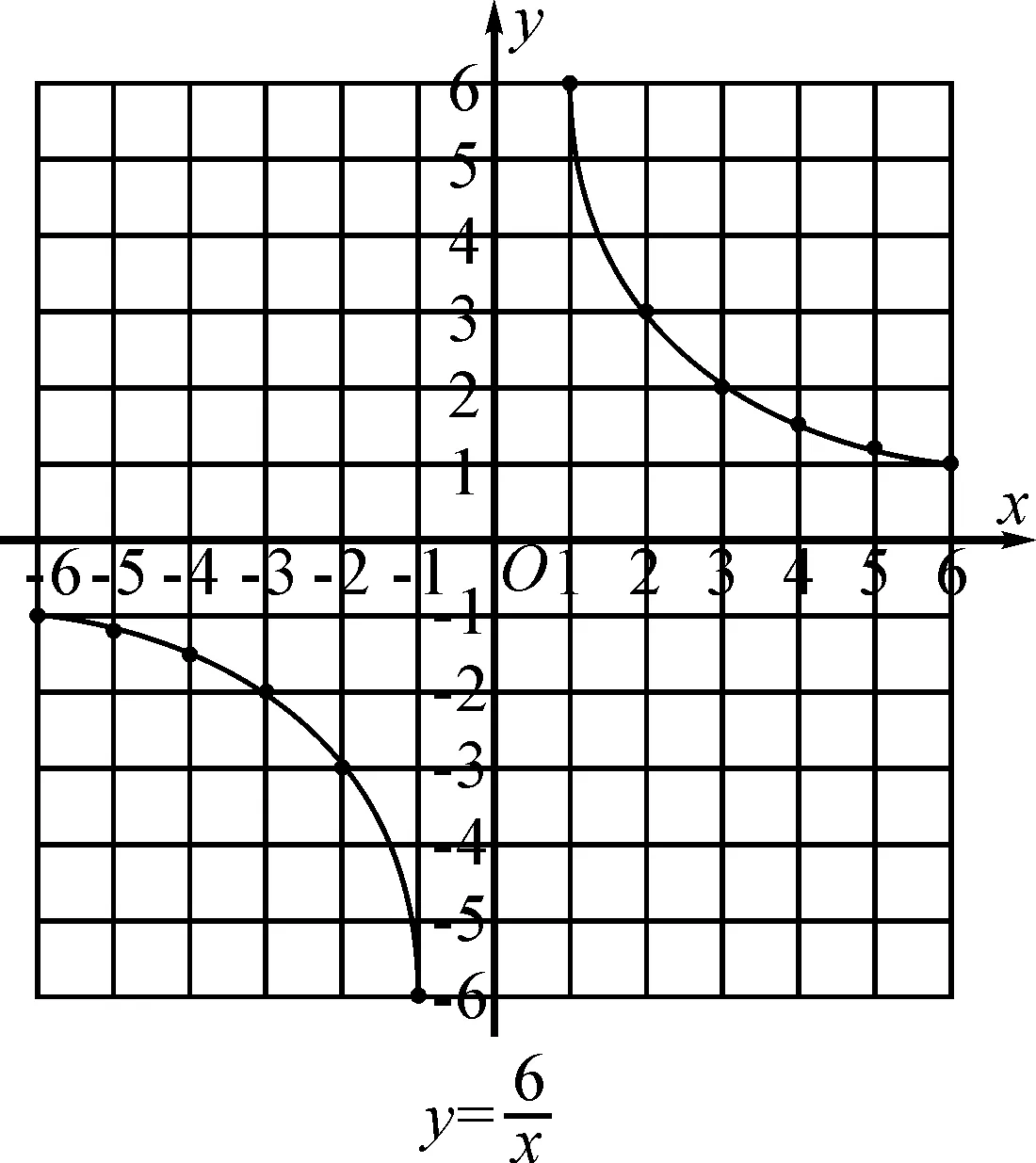
图2
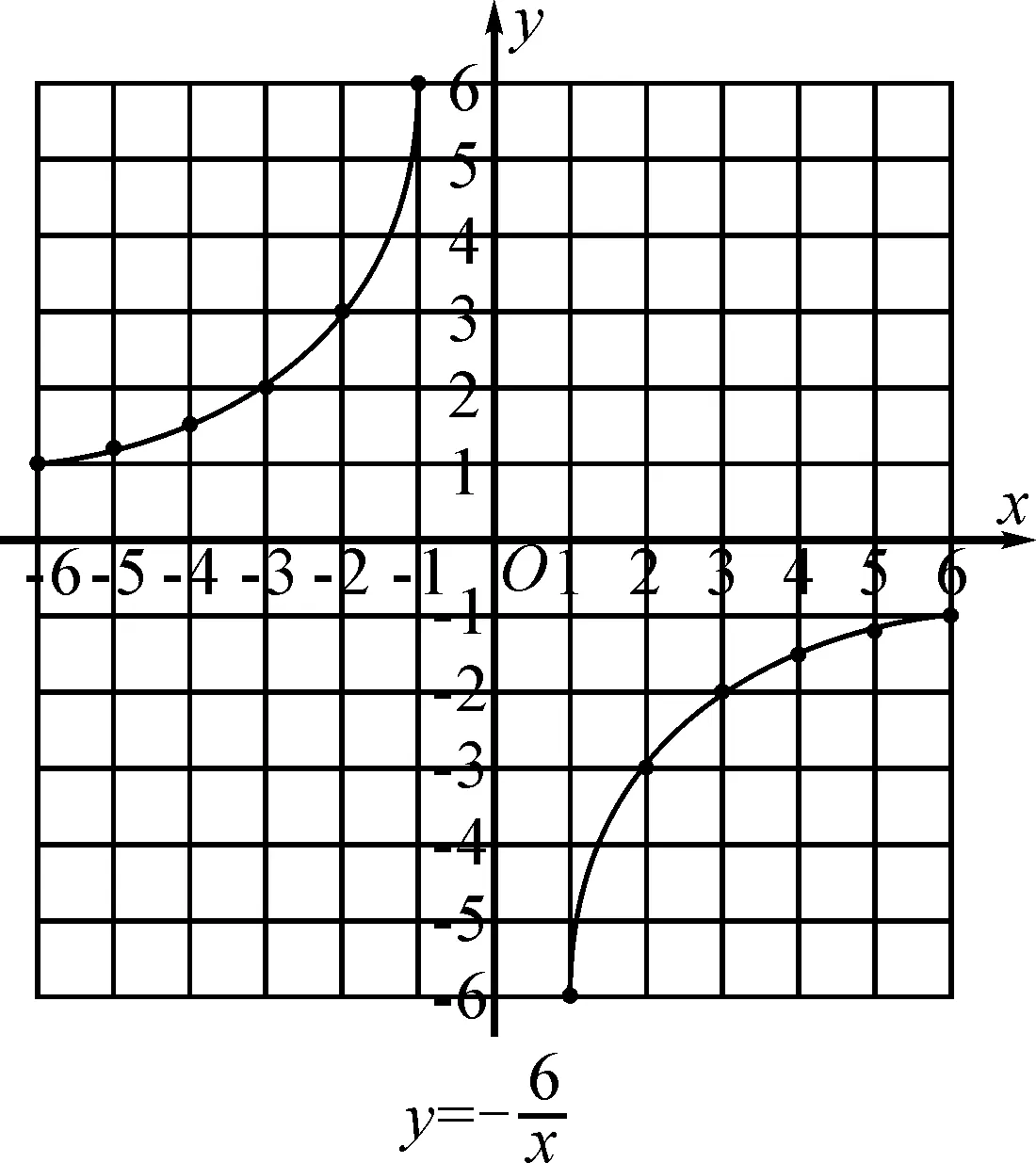
图3
设计意图:通过作出函数图象检验自己的学习成果,有助于掌握描点法.
生:这两个反比例函数图象都分为两部分;都接近坐标轴但不相交;都是中心对称图形;都是曲线.
师:同学们总结得非常全面!当k值不同时,对于所有的反比例函数来说,我们得出的结论是否成立呢?让我们一起借助计算机看看,当列出不同的k值时,所得结论与之前是否相同.
生:我认为可以称为双曲线.
设计意图:培养学生综合处理问题的能力,提高学生探索知识的能力.
3.3 总结反比例函数的性质
(1)反比例函数图象的位置见表2.

表2 图象位置
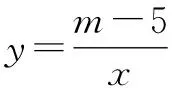
解:因为图象位于第一、三象限,所以m-5>0,解得m>5.
(2)反比例函数图象的增减性,见表3.

表3 图象增减性

A.y1>y2>y3B.y2>y1>y3
C.y1>y3>y2D.y2>y3>y1
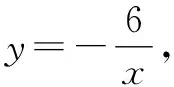
(3)反比例函数图象的对称性.
通过观察反比例函数的图象可以直观地看出它既是轴对称图形又是中心对称图形,对称轴有两条,为直线y=x和y=-x,对称中心为坐标原点.
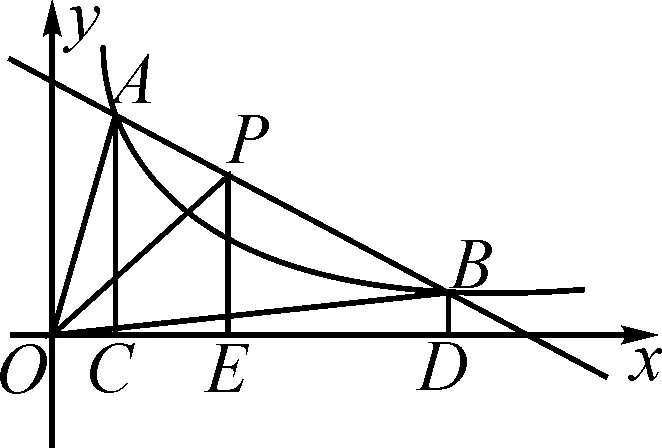
图4
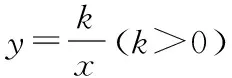
A.S1
C.S1=S2>S3D.S1=S2 师:通过这节课的学习,大家谈一谈有哪些收获? 学生1:通过这节课的学习,我知道了反比例函数图象的位置.当系数k>0时,图象位于一、三象限;当系数k<0时,图象位于二、四象限.通过这节课的学习,我能够通过判断系数k与0的大小关系,画出反比例函数图象的具体位置. 师:你理解的很到位. 学生2:我学会了可以通过取特殊值作出反比例函数图象. 师:很好. 学生3:我学会了判断反比例函数的增减性.当k>0时,图象在分别在第一、三象限内,y随x的增大而减小;当k<0时,图象分别在第二、四象限内,y随x的增大而增大. 师:很好.同学们,通过你们的回答,老师相信大部分同学已经很好地掌握了本节课的内容,大家在课下还要通过做题巩固本节课所学的知识. 课后发现一些后进生没有跟上老师的思路,讨论的效率不高.下次教学应该慢下来,询问一下班级的后进生是否有没听懂的地方,并要对学生的困惑之处予以解答.同时,改进学生之间的交流模式,可以采用几个优秀生带动几个后进生的模式,以提高讨论效率[2],兼顾大部分学生的学习. (1)重视对概念的深化理解. 重视对反比例函数概念的深化理解,在得到反比例函数的解析式后,需要通过做题来巩固所学.对简单的习题,让学生自行作答;对于学生解决起来有困难的问题,教师施以援手,给学生思路,简化学生的思考过程. (2)教学方法、教学手段要多样化. 教师需要采用多种教学手段及方法,促使学生聚精会神地听课.比如,教师可以变换音量与音调,让学生的注意力放在教师身上;可以设置小组内学习活动,以前后桌四人为一个小组,展开合作学习,同学之间集思广益,碰撞出思维的火花;还可以利用多媒体辅助教学,展示反比例函数图象的形成过程,让学生更加直观地感受反比例函数的本质特征,化抽象为具体,方便学生理解与领悟. (3)注重学生思维的培养. 数学的学习与学生思维的培养相互影响,尤其是函数的学习.函数的学习是承前启后的,将之前学习一次函数的方法迁移到反比例函数的学习中,使学生的函数学习融会贯通,从整体上把握函数的思想方法[3]. 教师对实际教学进行研究与反思是十分必要且不容忽视的一个环节.而函数是初中数学的重要板块,本文选取了“反比例函数”的实际教学片段进行深入研究,对教学的改进与提高提出了一些自己的感悟与理解,希望对今后的教学有所裨益.
3.4 交流体会,检测效果
4 教学反思
5 教学启示
6 结语
