基于数据可视化的高中生计算思维表现性评价研究

季金杰

（上海市格致中学 上海 200001）

一、引言

计算思维是高中信息技术学科核心素养的组成要素之一。计算思维评价是发展和培养学生计算思维的重要环节。计算思维评价一般有两种基本的价值取向。一种是对学习的评价，目的是验证计算思维培养的成效和学生计算思维的发展水平，对学生的学业成就进行认证和选拔。另一种是为了学习的评价，目的是更好地发展学生的计算思维，通过过程性评价和表现性评价，帮助教师及时了解和掌握学生计算思维的发展现状，使教师能根据评价结果，有针对性地调整教学设计，实施个性化教学，基于循证导向促进学生计算思维的持续发展。

已有的计算思维评价研究成果大多以“对学习的评价”为价值取向。例如，有学者开展计算思维评价微认证，评价学生是否达到预期的能力水平。［1］这是典型的对计算思维培养成效的评价和验证。国际上的不少计算思维评价项目基于这一评价理念。例如，西班牙学者罗曼·冈萨雷斯（Romaán-Gonzaález）开发的计算思维测试CTt（Computational Thinking test），包含28道测试项目，每道测试题均以“迷宫”或“画布”的形式呈现，测量学习者对基本计算概念的掌握情况以及使用编程解决相关问题的能力。［2］这是典型的终结性评价，仅能从认知、理解、应用等维度，检测学生在某一时间节点的能力水平，难以形成对学情发展的持续跟踪以及对教学改进的建议与反馈。

有学者对已有的计算思维评价工具进行研究后发现，国外对计算思维评价的研究成果大都将布伦南（Brennan）和雷斯尼克（Resnick）提出的计算思维评价的“三要素框架”作为理论基础，即以计算概念、计算实践、计算观念作为评价维度。［3］然而，“三要素框架”最初是美国麻省理工学院终身幼儿园研究小组在图形化编程的教学中构建的计算思维评价维度，未必适用于其他的教学内容和教学情境。

《普通高中信息技术课程标准（2017年版2020年修订）》（以下简称《新课标》）将计算思维学科核心素养的具体表现界定为“解决问题过程中的形式化、模型化、自动化、系统化”。此外，《新课标》对计算思维内涵的界定还进一步强调，在问题解决后要总结利用计算机解决问题的过程与方法，并迁移到与之相关的其他问题解决中。［4］

《新课标》对计算思维内涵与具体表现的界定与国际上开展的诸多计算思维评价项目所依据的理论基础不尽相同。基于《新课标》开展高中生计算思维评价，理应着眼于学生能否创造性地解决实际问题，重点关注学生在问题解决过程中的具体表现。

表现性评价是在尽量合乎真实的情境中，运用评分规则对学生完成复杂任务的过程或结果做出判断的评价方法。［5］在高中信息技术教学实践中，教师应秉持“为了学习的评价”的价值取向和发展理念，运用表现性评价，合理收集和应用评价数据，客观反映学生在问题解决过程中的实际表现、达到的表现水平以及在相关问题解决中的迁移能力，根据学生计算思维表现性评价结果，研究相应的教学决策和教学策略。

二、高中生计算思维表现性评价的维度建构与方案设计

（一）高中生计算思维表现性评价的维度建构

《新课标》将计算思维学科核心素养的具体表现界定为“解决问题过程中的形式化、模型化、自动化、系统化”。［6］基于此，高中信息技术学科开展计算思维评价的理想模式是以基于问题解决的项目活动或评价任务为统领，在学生解决问题的过程中，从形式化、模型化、自动化、系统化等方面评价学生的具体表现，从多个维度评估学生计算思维的表现水平。

然而，对于“形式化、模型化、自动化、系统化”的具体含义，《新课标》并未具体说明。因此，为构建高中生计算思维表现性评价维度，需进一步明确“形式化、模型化、自动化、系统化”的内涵。

美国国际教育技术学会（ISTE）和计算机科学教师协会（CSTA）将K-12教育中的“计算思维”定义为学生在问题解决过程中六个方面的表现：其一，用计算机或其他工具可处理的方式阐述和表达所要解决的问题；其二，分析并合理组织数据；其三，运用建立模型等抽象的方法来呈现数据间的关联；其四，通过设计算法，形成问题解决方案；其五，根据要实现的目标，应用各种可行的解决方案，从中找到效率最优的解决方案；其六，将问题解决的过程与经验，拓展和迁移到更广泛的问题情境中。［7］这一操作性定义将学生运用计算机解决问题的过程进行分解，明确了各环节的表现和评价要点。此外，在这一定义中，阐述和表达问题、组织数据、设计算法、形成问题解决方案、迁移运用等均与《新课标》对计算思维的界定相通。

根据《新课标》对计算思维内涵与具体表现的界定，笔者尝试将解决问题过程中的“问题分解”“抽象与建模”“方案设计”“效率优化”以及在解决其他相关问题中的“迁移应用”作为高中生计算思维表现性评价的五个维度。同时，借鉴美国国际教育技术学会和计算机科学教师协会对“计算思维”的操作性定义，笔者对各评价维度作解释和说明，如表1所示。

表1 高中生计算思维表现性评价维度及解释说明

（续表）

在教学中，开展基于问题解决的计算思维表现性评价，不仅要预先设计评价任务，还要结合评价任务，围绕上述评价维度，设计评价方案。在评价方案中，对于每一个评价维度，按表现水平由低到高划分为4个等级，明确达到每一个等级对应的行为表现，以此作为评价学生计算思维表现水平的标准。

（二）高中生计算思维表现性评价的方案设计——以“邮资计算”项目为例

在高中信息技术《必修1数据与计算》“算法与程序实现”单元的教学中，笔者设计了以“邮资计算”为主题的评价案例。在这一评价案例中，通过分析各维度的评价要点，设计评价方案，从而进一步梳理出计算思维表现性评价标准的设计框架。

1.项目任务

某市邮寄市内平信的邮资计算方式如下：

若总重量（含信封、信纸等）小于等于20克，邮资为0.8元。

若总重量超过20克且不超过100克，则在首重（20克）收0.8元的基础上，每加重20克，邮资增加0.8元。若加重部分不足20克，也按20克计算。例如邮寄一封总重量为40克的平信，则应支付邮资1.6元。邮寄一封总重量为31.92克的平信，也应支付邮资1.6元。

若总重量超过100克，暂作“超重”处理。

能否为邮局设计一个能够实现计算邮资的解决方案，输入信件重量，输出相应的结果。

2.评价要点分析

（1）问题分解

首先，教师按照计算机处理问题的方式分解项目任务，可将问题解决的过程分为三个环节：输入信件的重量；根据信件重量，计算其所对应的邮资；输出结果。其次，分析项目任务中需要用到的数据、数据类型和数值范围。在这一评价任务中，至少涉及两个变量，即信件重量和邮资，两者的数据类型均为实数型。

（2）抽象与建模

在“抽象与建模”维度，评价的要点在于学生能否准确建立邮资与信件重量之间的关系模型，既可以用分段函数来构建邮资与信件重量之间的关系，也可以运用分支结构设计流程图。

（3）方案设计

在“方案设计”维度，评价的要点是学生能否合理编写程序，将前一环节建立的邮资与信件重量之间的关系模型，转化为计算机可执行的问题解决方案。

（4）效率优化

在“效率优化”维度，评价的要点是学生能否分析、比较并找到效率最优的解决方案。这一维度的评价结果，较能体现学习者思维能力的差异。根据以往的教学实践，学生设计的问题解决方案大致可分为三类，三类方案之间存在效率差异且效率差异主要体现在邮资与信件重量之间的关系模型上。

方案一是通过五重分支结构的嵌套来实现邮资与信件重量的关系。

方案二是运用如图1所示的流程图作为描述问题解决方案的算法模型。在这一方案中，以信件的重量是否为20克的整数倍作为判断条件，根据判断结果，分别建立邮资与信件重量之间的关联。在信件不超重的前提下，不论信件重量是否为20克的整数倍，都可以通过双分支结构，实现对邮资的计算。

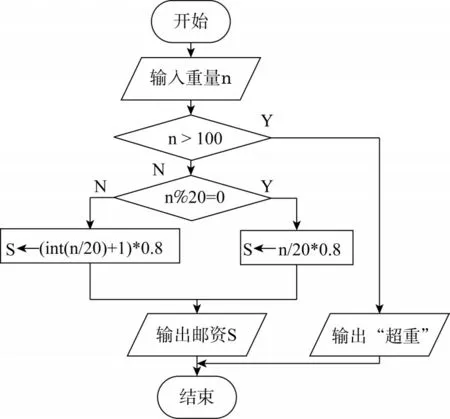
图1 用双分支结构的嵌套描述“邮资计算”评价项目的解决方案

方案三是运用如图2所示的流程图作为描述这一问题解决方案的算法模型。在这一方案中，在信件不超重的情况下，可以用一个普适性较强的表达式来描述邮资与信件重量之间的关系。由此，在获取信件重量后，仅需通过一次判断，即可输出相应结果。相较而言，这一解决方案的算法效率更高。

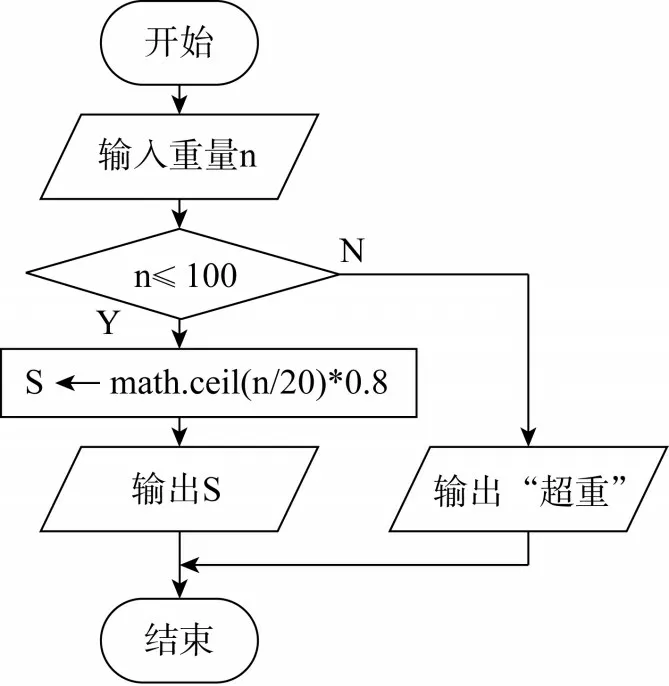
图2 用双分支结构描述“邮资计算”评价任务的解决方案

（5）迁移运用

在完成评价项目的实施、分析与讲评后，以一项与本项目相关的“停车费计算”问题作为课后练习，重点评价学生能否合理迁移问题解决的过程与方法，设计出算法效率较高的解决方案。

3.评价标准设计

以“邮资计算”项目为例，通过分析各维度的评价要点，将学生在各评价维度上的表现从低到高划分为4级表现水平，预估并描述学生在每个表现水平上对应的具体表现，由此形成了以“维度—水平—表现描述”为主干的评价标准设计框架。

如表2所示，在评价实施的过程中，教师可结合学生的具体表现，对照评价标准中的表现描述，确定并记录学生在各评价维度的表现水平。

表2 基于“邮资计算”项目的计算思维表现性评价标准

（续表）

三、基于数据可视化的高中生计算思维评价工具开发

（一）需求分析

笔者对52位具有高中信息技术新教材教学实践经验的教师进行访谈，了解高中信息技术教师对于运用数字化工具辅助开展计算思维表现性评价的实际需求和建议。通过对受访者基本观点的整合归类，可将教师对计算思维评价工具的使用需求归纳为以下几个方面。

1.评价数据的汇总与保存

在评价过程中，教师通常采用“一人一文档”的方式，通过组织一次基于问题解决的项目式评价，将学生在计算思维各评价维度方面的表现水平记录在电子表格中。教师普遍希望运用评价工具能对原本存放在电子文档中的评价数据进行结构化存储，汇总每一位学生在每一项评价任务中的评价数据，便于查询和分析。

2.评价结果的可视化呈现

尽管教师能够根据预先制定的评价标准，在学生解决问题的过程中，评价学生在各维度的表现水平，但使用数值来表示学生达到的水平等级，难以直观地描绘学生计算思维的发展情况，亦难以体现学生历次评价结果的纵向比较。接受访谈的教师大都希望以可视化的方式呈现评价数据，直观了解学生计算思维各评价维度的表现水平。

3.历次评价结果的跟踪与比较

作为一项为了促进和提高学生计算思维而持续开展的评价，计算思维表现性评价将伴随学生高中信息技术学科的整个学程。受访者建议，评价工具不仅要记录学生在历次评价任务中的评价结果，还应在积累评价数据的基础上，可视化呈现学生在整个学程中计算思维的发展轨迹。

（二）工具开发

根据受访者对计算思维过程性评价工具的使用需求和建议，笔者运用Python编写了由前端操作界面、后端功能模块和数据库组成的高中生计算思维表现性评价工具。该工具能够实现三个基本功能。其一，将原本以“一人一文档”的方式存储在电子文档中的评价数据，批量导入到数据库中。其二，以学生的学号为查询依据，以雷达图呈现学生在每个评价项目中各评价维度的表现水平。其三，以学生的学号为查询依据，以折线图呈现学生在历次评价中各维度表现水平的发展轨迹。

在数据库中建立数据表，用来存储学生在每一个评价项目的数据。数据表中共包含9个字段，字段名称、数据类型及相应说明如表3所示。在开展计算思维表现性评价前，教师需根据评价标准，预先设计电子表格模板，以记录学生在各个评价维度的表现水平。运用计算思维评价工具，可选择电子表格的存放路径，并将电子表格中的评价数据批量导入到数据库中。

表3 数据表字段解析

（三）评价数据的可视化呈现

1.用雷达图呈现学生计算思维的发展水平

笔者在高中信息技术必修课程的教学中，共组织开展4次基于问题解决的评价活动。为全面而直观地描绘学生在历次评价项目中计算思维的表现水平，以雷达图作为可视化呈现方式，如图4所示。当完成了若干次评价活动后，在评价工具中输入某一学生的学号，雷达图可以呈现学生在已完成的历次评价项目中的计算思维表现水平。

在图4所示的可视化评价结果中，共有三个雷达图，分别表示该学生在四次评价项目中的计算思维表现性评价结果。每一个雷达图均有五个顶点，表示该学生在“问题分解”“抽象与建模”“方案设计”“效率优化”“迁移运用”这五个评价维度上达到的表现水平。从图4中可以看出，该学生在“评价项目1”中表现总体一般，特别是在“效率优化”“迁移运用”两个维度的表现水平仅为1级。随着课程学习的不断深入，教师基于评价结果诊断学生计算思维发展的薄弱环节，对学生进行个性化辅导，在后两个评价项目中，学生的计算思维表现有了较全面的提高。

图4 用雷达图呈现学生计算思维表现性评价结果

2.用折线图描绘学生计算思维的发展轨迹

以学生发展为导向的计算思维评价，旨在促进学生计算思维各表现维度的全面发展。在教学与评价实践中，部分学生在“问题分解”“抽象与建模”等评价维度表现出较高水平，但在“方案设计”“效率优化”等评价维度中表现一般，表明这些学生在根据算法模型形成自动化解决方案、寻找最优的解决方案等方面存在学习困惑。为了持续引领学生计算思维的全面发展，评价工具可将学生在历次评价活动中五个评价维度的表现水平数据以折线图的形式呈现，便于教师观察学生计算思维各评价维度的发展轨迹。

如图5所示，折线图中的每一条折线表示学生在一个评价维度上的发展水平变化。图中的五条折线均呈上升或平稳的发展趋势，表明该学生在一学年的四次评价项目中，计算思维各评价维度的表现稳中有升。通过比较该学生在“评价项目1”（学程初期）和“评价项目4”（学程末期）中各评价维度的表现水平，也能从一个侧面反映出学习高中信息技术必修课程对于学生计算思维发展的成效。

图5 用折线图呈现学生在历次评价项目中计算思维的发展变化

四、结语

本研究以构建高中生计算思维表现性评价维度为逻辑起点，梳理了“问题分解”“抽象与建模”“方案设计”“效率优化”“迁移运用”五个评价维度的基本内涵，提炼了以“维度—水平—表现描述”为框架的评价标准设计样式，便于教师对学生问题解决过程中的具体表现划定水平等级。在不改变教师教学评价实施习惯的前提下，通过开发数字化评价工具，汇集每一位学生的评价数据，可视化呈现学生在各评价维度的表现水平，追踪学生计算思维的发展轨迹，从而建立了一套具有可操作性的高中生计算思维表现性评价实施路径。在后续的研究与实践中，可围绕信息技术赋能学生计算思维评价进行探索，挖掘学生计算思维表现的影响因素，从而帮助教师持续优化教学实践，促进学生计算思维的不断发展。