基于复杂网络的关联公共交通系统韧性分析

王淑良，陈 辰，张建华，栾声扬

(江苏师范大学电气工程及自动化学院，江苏 徐州 221116)

0 引言

城市公共交通系统是居民出行和城市职能发挥的基础工程设施，正常有序的交通系统对国家或地区的社会经济发展有着至关重要的作用。随着城市规模的快速扩大，部分特大城市的公交日均客运量已经突破千万。以上海为例，其轨道交通系统于2016年已承担起逾50%的公交客运量[1]。然而，在公共交通系统迅速发展的同时，自然灾害、恐怖袭击事件以及设备故障等突发事件的发生，使得系统风险增加，其安全运营也面临新的挑战和要求。由此可见，公共交通系统的运行安全问题应该且必须得到足够的重视，而保证公共交通安全运行的前提就是要清楚地认识网络拓扑结构及其韧性恢复水平。

公共交通网络建模及拓扑特性分析方面的研究很多，主要基于Space P和Space L两种空间形态进行建模，拓扑特性分析主要集中在度分布、聚类系数和平均路径长度等指标的统计分析[2]。然而，传统网络属性分类方法的拟合过程较为复杂，对于大规模网络分析效率较低。卷积神经网络作为一种具有深度结构和卷积计算的前馈神经网络[3]，由于其特征提取的准确性与分类的高效性特点，常被用来处理分类问题。在对真实网络的研究过程中，人们发现大多数现实网络并非单一网络，而是由多个网络相互耦合形成的，因此多层网络模型[4]被提出。顾名思义，多层网络模型是由多个子网络构成，各子网络之间通过相互协作或依赖关系进行耦合。近年来，多层网络分析借鉴了渗流理论等统计物理学的思想，在其结构鲁棒性研究上取得了显著进展[5]。Buldyrev等[6]对完全关联的两个网络进行分析，并发现系统发生了突变，这说明在关联网络中，关键节点的失效容易导致“级联失效”的发生，从而导致大规模的网络故障。其他学者通过考虑部分耦合、多个网络耦合及不同耦合关系等进行拓展，从而提高了对耦合网络的结构认识[7]。

由于网络故障的必然性，网络的韧性分析成为一个需要关注的问题。韧性强调的是网络抵御风险故障的能力和恢复能力，Mattsson[8]通过干扰下网络的性能变化来进行韧性分析。Fang[9]研究了自然灾害下的韧性评估以及不同修复策略的优缺点。Gong等[10]则提出优先恢复重要节点的择优恢复策略，根据择优恢复序列发现可以较好地表征节点重要性的评估指标是韧性恢复的首要问题。

近年来，学者们提出了多种节点重要性评估指标和算法，包括度、接近中心性、介数中心性、特征向量和PageRank[11]等。但以上方法都是从不同角度提出的评估节点重要度的指标，可能存在一定的片面性和局限性，而关于综合多因子的节点重要性分析方法研究甚少。Zhao[12]根据层次分析法得到节点评价指标的权重，确定地铁网络中的配送枢纽。Peng[13]通过结合熵权法和层次分析法来评估全球海运网络中港口的综合竞争力。而公交和地铁作为城市内部重要的公共交通系统，它们之间相互影响、密切联系。基于此，本文通过对城市公交、地铁系统之间依赖关系的分析，构建公交-地铁耦合网络模型，借助深度学习分析耦合网络的拓扑类型，并结合熵权法[14]与最优理想解距法[15]提出高效的韧性恢复策略。

1 公共交通网络拓扑特性分析

1.1 耦合网络模型建立

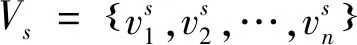
1)设置耦合距离D值；

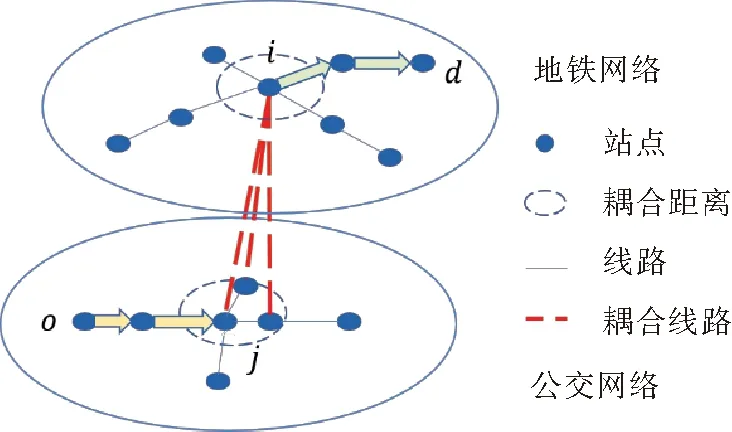
图1 耦合网络建模示意图Fig.1 Schematic diagram of interdependent network modeling

4)重复步骤3)，直到检查完地铁站点与所有公交站点之间的地理距离；

依据以上步骤，可以识别所有耦合站点对，通过耦合站点将公交网络与地铁网络相互关联。若耦合距离内存在多个公交站点，则分别对其进行连接，如图1所示。

图2 经典网络的邻接矩阵图片化Fig.2 Adjacency matrices for classic networks in the form of pictures

1.2 基于深度学习的交通网络拓扑特性分析

网络拓扑分析是网络科学实证研究的基础。对于不同拓扑结构的网络，其网络属性也不相同。常见的网络模型有ER随机网络、BA无标度网络以及WS小世界网络。随着深度学习理论的发展，CNN模型得到了广泛的应用[16]，主要通过卷积层、池化层和全连层来实现输入输出的转化。由于其特征提取高效、数据格式简单以及分类准确等优点，本文结合CNN模型提出网络属性的分类方法。如图2所示，邻接矩阵常用来描述网络拓扑结构，其中“1”表示两节点之间存在边，而“0”表示两节点之间无连接。本文将邻接矩阵中的“1”和“0”分别用黑白表示，获得邻接矩阵的图片形式。通过对比三种经典网络的邻接矩阵图片可以发现，BA无标度网络中的白点大多分布在图片左上角，WS小世界网络中的白点则位于图片对角线上，而ER随机网络中的白点是均匀分布的。依据不同网络的邻接矩阵图片的明显特征，本文结合CNN实现对大型真实网络的拓扑结构进行分类。

2 基于熵权法与最优理想解距法的韧性提升策略

2.1 交通系统韧性分析

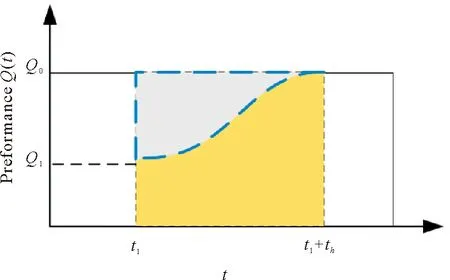
图3 韧性恢复示意图Fig.3 Schematic diagram of resilience recovery

对于大多数实际网络而言, 网络都具有一定的抵御风险能力和恢复能力，而韧性提升策略是指在原有网络上对关键节点进行补救和修复，从而使其逐步恢复原有功能。在已知全部待恢复站点的情况下，研究各站点的最佳恢复时序具有重大的意义。Bruneau[17]提出，使用“韧性三角”的概念来量化网络恢复后的性能损失，故障后网络的性能恢复变化如图3所示，t1为事件发生时间，th为系统从故障中完全恢复到正常状态所需时间，Q0为攻击发生时的初始性能，Qi为系统由事件引起的最低性能，图中阴影部分则为系统恢复后的性能损失，即系统初始状态性能Q0覆盖面积与攻击系统修复过程中性能覆盖面积之差。而修复效果的量化则是两个面积的比值，恢复效率R对应公式为

(1)

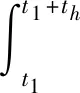
(2)

2.2 基于EWM-TOPSIS的节点重要性排序

在择优恢复的基础上，对关键节点的识别与确定就尤为重要。根据不同节点重要度评估方法可以给出不同的节点修复策略，依此来分析不同修复策略对于网络修复能力的影响。本文以度、介数和接近中心性等节点重要度评估指标为基础，结合熵权法(Entropy Weight Method，EWM)和理想解距法(Technique for Order Preference by Similarity to Ideal Solution，TOPSIS)提出一个新的综合指标来确定节点恢复序列。

度中心性(Degree Centrality,DC)表示为与节点i有直接联系的网络节点比例，反映了与其他节点的关联性。其中，ki为节点i的度，N为网络规模。

(3)

介数中心性(Betweenness Centrality,BC)刻画了节点对网络流量的控制力，即介数中心性越高的节点有越多的最短路径从该处经过。其中，Bi为经过节点i的最短路径比例。

(4)

接近中心性(Closeness Centrality,CC)反映了乘客从给定站点到网络中其他可达节点所需的时间。dij为节点i和j之间的最短路径长度，可看作节点i和j之间平均出行时间的度量。

(5)

以上指标分别从不同角度对节点重要性进行评估，但由于其侧重点、物理意义等不同，只能反映节点的单边特性。因此，本文提出基于EWM-TOPSIS的综合指标来评估节点重要性，并得到高效的恢复序列。熵权法通过熵原理分析各个评价指标之间相对离散程度，而TOPSIS可最大限度地规避人为因素对准确性的影响，具体步骤如下：通过节点重要度指标j评估节点vi而给出的节点重要度为Yij(i=1,2,…,n;j=1,2,…,p)，则原始矩阵Y=(yij)表示为

(6)

1)初始化原始矩阵。为消除指标取值范围及计量单位的差异，首先对指标进行标准化处理：

(7)

2)计算每个指标的客观权重。首先计算每个评估指标的信息熵：

(8)

则指标j的权重系数为

(9)

3)归一化标准矩阵：

(10)

接着根据熵权法得到的权重,来构造加权矩阵：

(11)

4)找出指标到理想解的距离。首先找出各项指标的最优值和最劣值：

(12)

接着计算各个评价对象与最优值和最劣值之间的距离，计算过程为

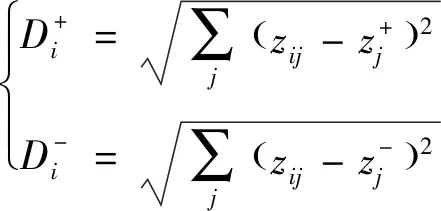
(13)

5)计算每个评价指标与最优值的相对接近度:

(14)

6)最后得到节点重要性排序：

(15)

3 案例分析

3.1 武汉市相依交通网络建模

武汉市作为华中地区的中心城市，是中国内陆最大的水陆空重要交通枢纽。本节以武汉市公共交通网络为例，构建相互依赖的公共交通网络模型，利用深度学习对其拓扑结构进行分析，同时量化评估系统的韧性，结合EWM-TOPSIS探索高效的韧性恢复策略，为公共交通基础设施的运行及安全提供保障。

城市公共交通系统中各站点具有独特的地理特征，地理特征的差异性表示每个站点所处区位的土地利用性质、人口密度和其他局部特征之间的差异，进而导致了网络中各节点演变规律和发展特征的差异。因此，为建立贴近实际情况的城市公共交通耦合网络模型，本文利用 Python 语言编写数据爬取算法从 8684 公交网(https://www.8684.cn/)得到公共交通信息，为准确分析公共交通网络的实际演变特征等研究提供基础支撑。站点经纬度信息获取则是基于公共交通信息，结合高德地图API，主要信息获取流程为：

1)读取已获取的站点信息数据；

2)调用 Place API，采用顺序遍历法，遍历站点名称得到对应站点的经纬度信息；

3)修正数据，对由于站点名称差异性存在的遗漏站点信息进行处理，并对自环及独立线路进行删除；

4)存储数据，对站点及对应线路信息、经纬度信息进行存储。

通过上述方法，获得武汉市目前有正在营运常规公交站点3 000多个，轨道交通线路8条，轨道交通站点210个(不考虑自环与孤立公交线路)。本节以耦合距离为500为例，构建武汉市相依公共交通网络，其中包含3 922个节点，6 586条边。

3.2 公共交通网络拓扑特性分析

通过不同的网络统计指标，可以得到实际交通系统的网络特征，常见的统计特征包括节点度和度分布、累计度分布、平均路径长度、聚类系数等，武汉市交通网络统计特征如表1所示。其中，耦合网络平均聚类系数远大于单一网络，说明物理空间上联系较为密集；平均最短路径小于公交网络，可以发现耦合网络符合无标度特性。上述方法虽然从网络的统计指标计算来对其拓扑特性进行分析，但其度分布难以拟合，且无法对大规模网络进行快速分类。深度学习的高质量分类特性在不考虑网络特性的情况下，为网络的拓扑分类提供了便利。

本文构建的CNN模型如图4所示，包括2个卷积层、2个池化层以及4个全连接层。为验证该模型的有效性，首先设置50，60，70和80节点的网络，对其进行分类训练。而对于大规模节点的网络则截取其数据矩阵的中心部分，既简化了计算复杂度又很好地保留了网络特征。每种网络类型生成700个，训练集和测试机分别设置为500和200，其分类结果如表2所示。

表1 武汉市交通网络拓扑特性统计Tab.1 Statistics on topological characteristics of Wuhan transportation network

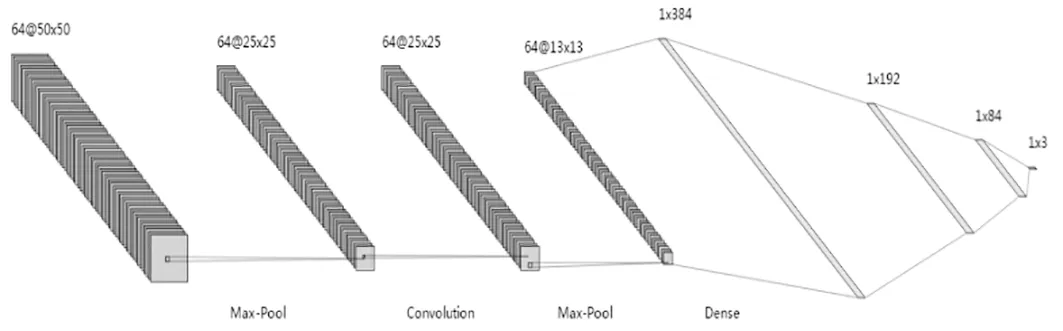
图4 CNN模型示意图Fig.4 CNN model

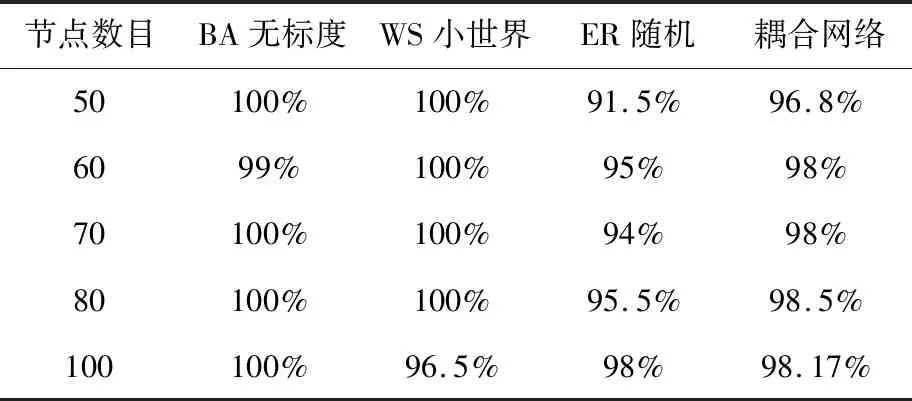
表2 基于CNN的经典网络分类召回率Tab.2 Classification recall for classic network based on CNN

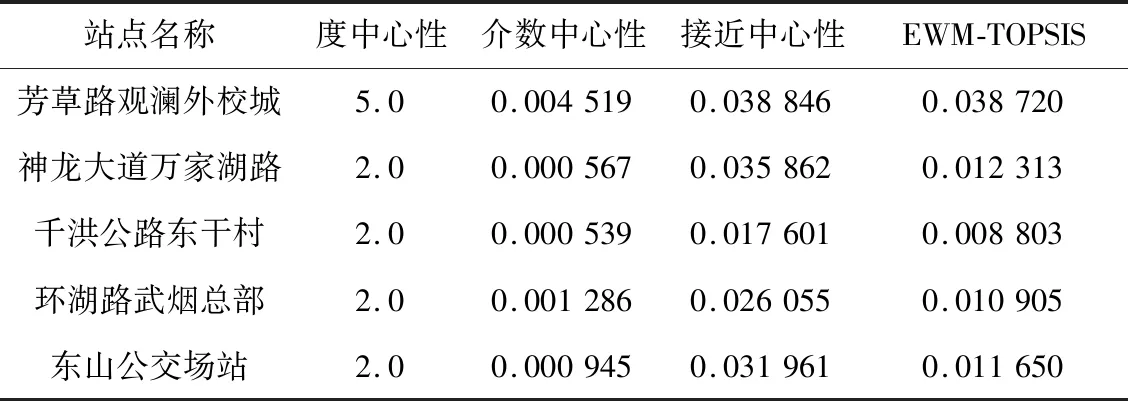
表3 基于多种节点重要度评估指标的重要度Tab.3 Nodes importance based on different evaluation indicators

由表2可知，节点数目小于100的BA网络和WS网络，其召回率接近100%；而对于节点数较大的BA网络和WS网络，其召回率下降至97%到98%之间。对于不同节点数的网络，其整体召回率为96%至98%。根据分类结果，相互依存的公交-地铁网络属于WS小世界网络。根据WS小世界网络的拓扑特性，即平均距离小、聚类系数大，实际公交网络的两站可通过短路径到达，网络密集、可达性高。平均路径长度可以看作是可达两站点平均经过的站点数，反映了网络的连通性和换乘的便利性。

3.3 基于熵权法与最优理想解距法的韧性提升

首先根据不同的节点重要度评估指标，可以给出不同的节点重要度评估值，如表3所示，给出随机5个站点的不同重要度评估。基于节点重要度评估的结果，可以构建多种修复策略。依据1.1节韧性分析可以得知，每个恢复策略的效率是通过计算恢复曲线和Y轴面积来衡量的，即面积越大恢复效率越高。假设公共交通网络在节点故障比例p=10%的状态下进行恢复，分别统计不同策略下的恢复顺序。

图5和图6分别给出了不同网络恢复过程的LCC和NE变化曲线，不同颜色曲线代表不同恢复策略下网络性能的变化。从图5a可以看出，在恢复节点较少的情况下，不同恢复策略对网络LCC的影响趋势保持一致。对比图6a发现，不同恢复策略对于同一网络的NE影响不同，且本文提出的EWM-TOPSIS法在基于NE的韧性计算下效果较优，即在相同时间步长的恢复下，韧性三角形面积最大。图5b和图6b表示公交网络的恢复过程。随着节点的恢复，LCC与NE值都呈上升趋势。与网络效率不同，LCC的上升曲线有多个骤增部分，这是由于部分关键节点的恢复，使得多个簇团连接至最大团导致。

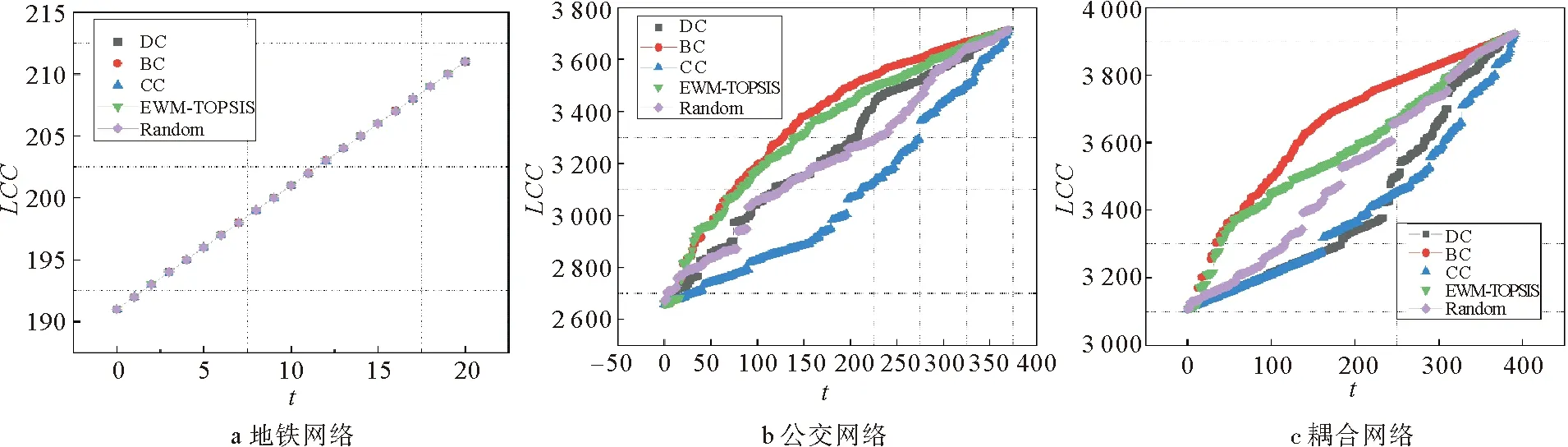
图5 3个网络恢复的最大团尺寸对比图Fig.5 Comparison of the largest connected component of the three network recovery processes

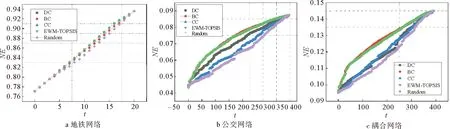
图6 3个网络恢复的网络效率对比图Fig.6 Comparison of the network efficiency of the three network recovery processes

图5c，图6c为公交-地铁耦合网络的恢复过程。由图5c可以发现，在对前25%的节点进行修复时，基于BC和EWM-TOPSIS修复策略的效果类似且较优，但随着节点的继续恢复，EWM-TOPSIS修复变化逐渐减小。对比图5b可以发现，只有在耦合网络中，基于BC修复的LCC值远高于其他修复策略。这是由于耦合网络中换乘边的增加，使得出行路径的选择更加丰富，从而导致恢复节点的介数值越高，该节点连接至最大团的概率越大。由图6c可知，BC和EWM-TOPSIS韧性曲线类似且韧性面积最大，表明恢复效率较优。

4 结论

随着城市的不断扩张与发展，城市公共交通系统也愈加复杂。本文以复杂网络理论为基础，构建公交-地铁耦合网络模型。依据深度学习来对网络拓扑属性进行分类，结合熵权法和最优理想解距法对单一节点重要性指标进行改进，提出EWM-TOPSIS综合指标应用于网络韧性恢复过程中，最后以武汉市公共交通网络为例进行分析，验证了该方法对于地铁公交网络节点重要度衡量的有效性。

另外，本文所提出新的评估节点重要性的指标主要是基于度值、介数和接近中心性构建而成，下一步将考虑交通流量和时间等因素，从多维度来评估节点的重要程度。由于本文所提方法的普适性，在未来工作中，可进一步分析该方法在其他基础设施系统上的应用。