一个偶数阶导数非负的Hermite-Hadamard型不等式及其应用

孟 晴,吴艺婷

(中国计量大学 理学院,浙江 杭州 310018)

设f:[a,b]→是连续凸函数,则著名的Hermite-Hadamard不等式表述为[1]

(1)

近年来,有许多学者对该不等式进行了改进和推广[2-7]。文献[8]中,Dragomir和Agarwal得到如下关于Hermite-Hadamard不等式右侧和中间项之差的恒等式:

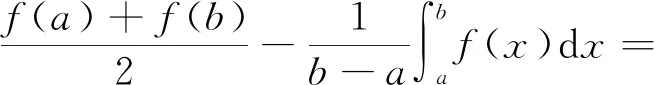
(2)

并利用该等式导出当|f′|为凸函数时的Hermite-Hadamard型不等式:

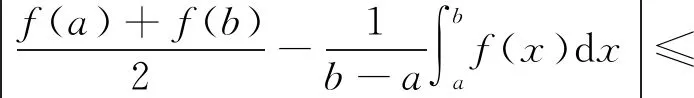
(3)

文献[9]中,邓勇平和吴善和在|f(n)|为凸函数的条件下,得到如下涉及高阶导数的Hermite-Hadamard型不等式:

(4)

本文将在f(2n)连续且非负的条件下,建立一个新的涉及高阶导数的Hermite-Hadamard型不等式。

(5)

为Schur-凸函数。褚玉明等人在文献[14]中证明了当f为凸函数时,

Ψ(x,y)=

(6)

为Schur-凸函数。本文将利用新建立的Hermite-Hadamard型不等式研究一个新的含变限积分的Schur-凸函数,并利用它导出著名的Bullen不等式[15]。

1 预备知识

定义1设f为区间[a,b]上的函数,若对任意x1,x2∈[a,b]和任意λ∈[0,1]有

f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),

则称f为[a,b]上的凸函数。

定义2[16]设Ω⊂n,x=(x1,x2,…xn)∈Ω,若对任意n×n置换矩阵P,有Px∈Ω,则称Ω为对称集。

定义3[16]设Ω⊂n为对称集,φ:Ω→,若对任意x∈Ω和任意n×n置换矩阵P,都有φ(Px)=φ(x),则称φ为Ω上的对称函数。

定义4[17]设向量x=(x1,x2,…,xn)∈n,y=(y1,y2,…,yn)∈n,x[1],x[2],…,x[n]表示x中分量的递减重排,即x[1]≥x[2]≥…x[n],若x,y满足：

则称x被y所控制,记作xy。

定义5[17]设Ω⊂n,φ:Ω→,若对Ω中任意满足控制关系xy的x=(x1,x2,…,xn)和y=(y1,y2,…,yn)有

φ(x1,x2,…,xn)≤φ(y1,y2,…,yn),

则称φ为Ω上的Schur-凸函数。

引理1[17](Schur-凸函数判定定理)设Ω⊂n为有内点的对称凸集,φ:Ω→在Ω上连续,在Ω的内部可微,则φ为Ω上的Schur-凸函数当且仅当φ在Ω上对称且对任意x=(x1,x2,…,xn)∈Ω有

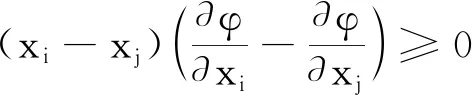
2 积分恒等式

引理2设f:[a,b]→,若f(2n)(n≥1)在[a,b]上连续,则对λ∈[0,1],有

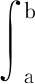
(7)

证明:当n=1时,

运用两次分部积分,得

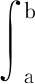
所以当n=1时,等式(7)成立。

假设当n=m时式(7)成立,即

(8)

运用分部积分,得

(9)

将式(8)代入式(9),得

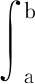
所以当n=m+1时,等式(7)成立,故对任意自然数n≥1,等式(7)成立。

因此,引理2得证。

3 Hermite-Hadamard型不等式

事实上,若f(2n)(n≥1)在[a,b]上连续且非负,则式(7)中的A2n≥0,于是,我们得到如下结果:

定理1设f:[a,b]→,若f(2n)(n≥1)在[a,b]上连续且非负,则对λ∈[0,1],有不等式

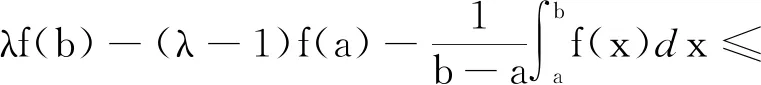
(10)

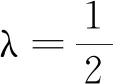
推论1设f:[a,b]→,若f(2n)(n≥1)在[a,b]上连续且非负,则有不等式

(11)

注2在推论1中令n=1,即得如下结果:

推论2设f:[a,b]→,若f″在[a,b]上连续且非负,则有不等式

(12)

4 函数的Schur凸性

本节利用定理1中的Hermite-Hadamard型不等式证明一个含变限积分的函数的Schur凸性。

定理2设f:I⊆→,若对n≥1,f(2k)(k=1,2,…,n)在I上连续且非负,则

S2n-2(x,y)=

(13)

是I2上的Schur-凸函数。

证明显然S2n-2(x,y)是I2上的对称函数。当x=y∈I时,对任意t0∈I,有

(14)

同理,可得

(15)

因此,由式(14)和式(15)知当x=y∈I时,

(16)

当x≠y∈I时,

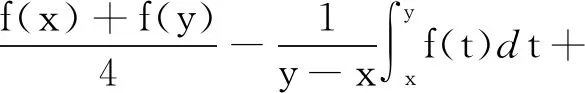
对S2n-2(x,y)分别关于x,y求偏导,得

(17)

(18)

利用式(17)和式(18)得

根据定理2的条件,f(2n)在I上非负,应用推论1中的不等式得到

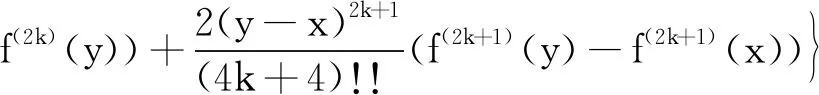
(19)

由于

和

将其代入式(19)得

(20)

根据定理2的条件,f(2k)(k=1,2,…,n)在I上非负,可知f(2k)(k=1,2,…,n-1)为I上的凸函数,由凸函数的定义得到对任意n≥1,

(21)

由式(16)和式(21),运用Schur-凸函数的判定定理(引理1)知S2n-2是I2上的Schur-凸函数。

从而定理2得证。

注3当n=1时,由定理2得到如下推论:

推论3设f:I⊆→,若f″在I上连续且非负,则

S0(x,y)=

(22)

为I2上的Schur凸函数。

注4由定理2知,S2n-2(x,y)是I2上的Schur-凸函数,利用熟知的控制关系

根据Schur-凸函数的定义,可得

由上面不等式,即得如下推论。

推论4设f:I⊆→,若对n≥1,f(2k)(k=1,2,…,n)在I上连续且非负,则

(23)

特别地,在不等式(23)中取n=1,得到著名的Bullen不等式,即

(24)

5 结 语

本文建立一个关于高阶可微函数的积分恒等式,然后利用该恒等式导出一个偶数阶导数非负的Hermite-Hadamard型不等式。作为应用,我们将得到的新Hermite-Hadamard型不等式用于证明一个含变限积分的函数的Schur凸性,并进一步由该函数的Schur凸性导出Bullen不等式。结果表明,通过构造Schur-凸函数,运用本文的方法可以推广和改进许多经典不等式。