基于行波非接触式牵引供电故障精确定位系统研究

2023-01-11杨国栋

电气化铁道 2022年6期

杨国栋

0 引言

牵引供电系统是现阶段我国轨道交通主要电力来源，而牵引供电系统一旦发生故障，直接影响铁路安全稳定运行，甚至可能造成不良的社会影响。接触网是铁路牵引供电系统的重要组成部分，一般处于自然环境恶劣区域，受到自然环境、恶劣天气的影响，易发生各类故障跳闸，供电臂长度一般在20～30 km，其运行维护采用人工巡线方式不仅花费大量的人力物力，而且工作效率极低，一旦遇到极端天气，极易造成重合闸失败。通过人工巡线排查故障往往需要花费大量时间，研究一种科学合理有效的故障测距手段显得极为重要。

在现阶段，接触网故障测距的主要方法为上下行电流比法、吸上电流比法、横联线电流比法，上述方法基本均为阻抗法故障测距原理，无论何种方法都或多或少受到系统运行方式、接地过渡阻抗的影响，存在一定的局限性。而行波法故障测距基本不受系统及过渡电阻大小的影响，其又分为单端法、双端法、网络算法等一系列故障测距手段，无论采用哪种算法进行行波法故障测距，影响其故障测距精度的因素均为行波在接触网中传输的波速以及行波到达监测终端的波头时刻，只需克服上述两个因素的误差影响即可实现故障精确定位。

近年来，随着传感器精度的提升以及数字化处理手段的提升[1，2]，行波法故障测距中的对时问题以及行波波头时间的处理问题得到了解决，因此行波法故障测距得以实现用于现行的电力线路故障测距[3，4]。传统的应用于电力线路故障测距的监测终端往往是采用接触式采集终端设备，其与导线直接接触，安装、更换工艺复杂，需将线路全线停电后进行安装，针对于重点负荷、无法停电线路极为不便。本文提出一种基于非接触式的牵引供电系统故障测距手段。

1 非接触式监测系统

非接触式故障测距手段最早提出于21世纪初期，最早应用于输电线路上，其监测原理是采用探头靠近被测线路，利用线路、杂散电容、探头电容中间构成的回路进行检测，通过对探头的振动频率监测进而计算线路电压，但由于测量带宽受到探头振动频率的影响以及杂散电容不可量化的影响，采用探头进行电压测量可能存在电压失败或测量精度过低的问题[5～7]。

本文提出一种改进的电压传感器，应对于接触网供电线路进行电压量的采集，其测量带宽可达100 MHz以上，对单线直供线路进行采集，在采集到交变信号后，对采集信号进行分类处理，通过判定工频信号的有效性进行接触网直供线路的故障跳闸判定，对于已发生跳闸的线路，选用合适的小波变换算法进行波头的识别，从而计算出发生故障跳闸的短路接地点。图1所示为非接触式监测系统的工作流程。

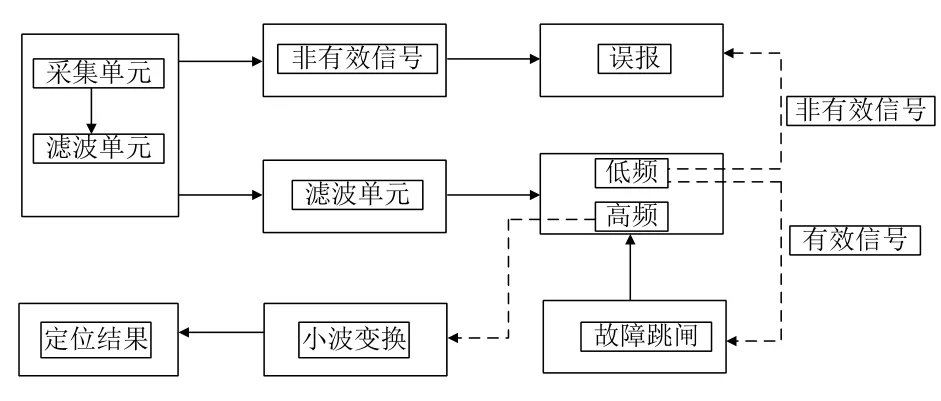
图1 非接触式监测系统工作流程

1.1 非接触式电压传感器

参考文献[6]中第一次提及非接触式故障测距的方式采用探头的振动频率进行线路电压的测量，该类测量方式虽然受限于探头测量带宽限制，但作为初代非接触式电压量测量模型，为非接触式测量提供了理论依据。本文提出一种基于电容分压的非接触式电压传感器，基于现行的直供供电方式进行线路电压、故障信息的采集[8～11]。利用电场耦合原理，采用双极板形式进行线路电压的测量；由于接触网线路周围存在电力自闭贯通线路以及部分高压输电线路，为屏蔽其他现场电场干扰，传感器外壳采用锰铝合金材料，其具备良好抗腐蚀性能的同时，可实现对外界静电、交流电场的屏蔽，从而实现非接触式电压测量。

图2所示为应用于直供方式下接触网线路的非接触式电压传感器，该传感器采用双电容极板进行被测导线电压测量，相比传统的探头式电压测量，其具有更高的带宽测量范围以及更好的频率响应特性，其输出呈现更好的线性特征，无论对于工频低频稳态，还是行波高频暂态，都可实现电压信号采集，图3为非接触式电压传感器工作原理图。

图2 非接触式传感器实物

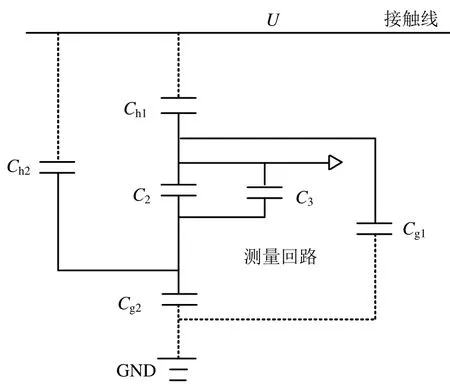
图3 非接触式电压互感器测量原理

非接触式电压互感器采用双极板式结构进行电压测量，Ch1、Ch2分别为接触网线对双极板电容，C2为串联电容，C3为测量回路电容，为不影响测量精度，采用与C2同等量级的电容单位进行测量阻抗匹配，C3进入运放后输出电压信号，Cg1、Cg2为双面电容对地杂散电容，U为被测线路电压，则可得C2两侧进入运放电路的测量电压UC为

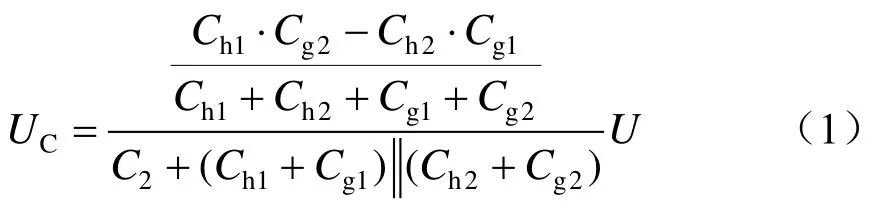
基于参考文献[10]中提到采用双极板电容测量电压时，高压臂电容约为0.5 pF，低压臂电容约为1.3 nF，且两极板之间距离d= 20 cm时电压测量为最精准值，在保证输出信号为线性的同时，也能保证高频暂态信号的快速响应特性。对于杂散电容Ch1、Ch2、Cg1、Cg2，其电容的量级单位为 nF级，因此测量电压基本位于C2两端，此时为反馈测量电压的准确性以及阻抗的匹配性，在C2上并联同量级单位的电容即可实现，在本文中出于电压精度的考虑，选取C3为300 nF，此时可形成约为300∶1的电压值测量。

1.2 RC处理积分回路

由式（1）可知，本电压互感器采用纯容性，而在利用电容式电压传感器进行信号测量时必须使用积分器进行信号的还原，将采集的信号输入RC积分器中即可实现。对于RC积分器的选定，若采用不合适的RC积分器可能导致信号还原出现问题。如果RC积分器参数选择过大，将直接影响高频响应速率，更有甚者导致在波形处理时出现波头偏移及波头时刻错误的情况；如果RC积分器选用的参数过小，对于高频信号可能出现关键点遗漏的情况，最终还原性能表现较差；因此合适的RC积分器参数选择显得极为重要[12]。

通过多次试验选取RC积分器参数，选取R为80 Ω，C为320 pF，此时RC积分器对线路的信号还原度最好（图4）。选取上述RC参数后，此时原始波形的上升沿时间t0为6.4 μs，而积分反馈输出信号响应时间t1为7.8 μs，则RC积分回路的动态响应时间t及系统采样响应截止带宽f为

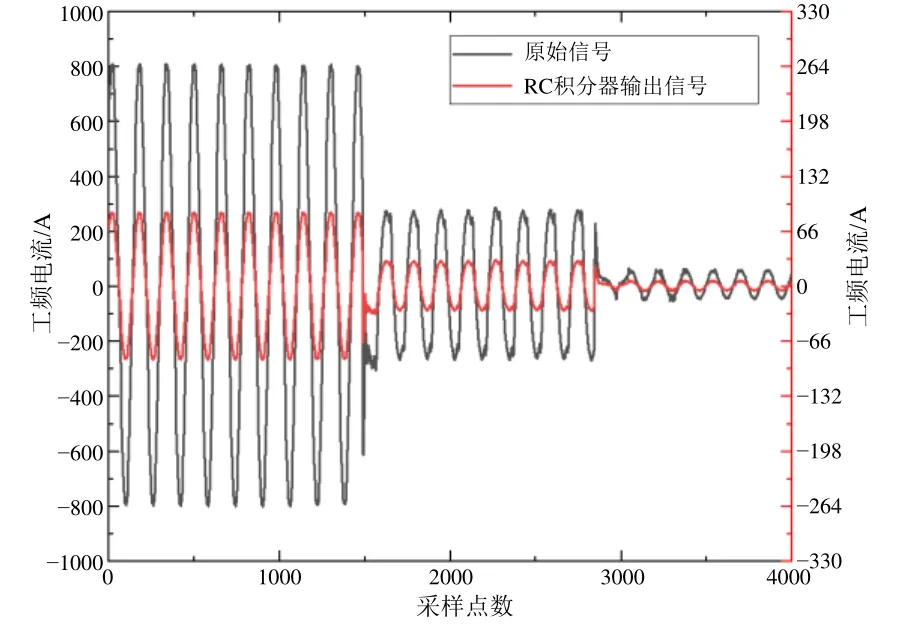
图4 RC积分器输入输出对比

如图4中所示，选取RC积分器参数后可实现信号的理想还原，在满足了响应截止高频率的同时，RC积分器响应时间较短，在实验环境下，非接触式监测传感系统可实现直供接触网线路的信号采集与还原。下文将详细阐述非接触式监测终端在进行行波故障测距时系统数据处理算法。

2 非接触式牵引供电系统工频电压判定逻辑

本文利用双极板式传感器对直供接触网线路进行故障精确定位，采用电容分压形式进行线路电压测距，通过后端RC积分电路实现接触网线路电压的还原[13～15]。

2.1 有效值计算

非接触式传感器采集到工频电压信号时，首先对工频信号进行快速傅里叶积分变换，通过工频信号主频率分布进行信号选择性判定，当傅里叶积分变换分解出主频率为 50 Hz时进行工频的有效值计算，有效值计算是通过求对应通道数据的均方根实现。设置采样点为pi，一个周期内总采样点数为n，平均值为X，有效值为yRMS，则关系式可以表示为

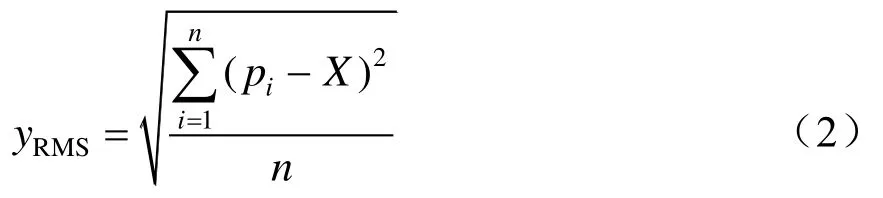
当每一个周期的有效值计算完毕后，进行缓存，共缓存3个相邻半周期（取10 ms为半个周期）的有效值，用于触发判断。

2.2 工频电流增量触发逻辑

对缓存的 3个相邻半周期的工频电流有效值进行计算，故障工频增量保护触发逻辑示意如图5所示。系统电流增量触发逻辑如下：

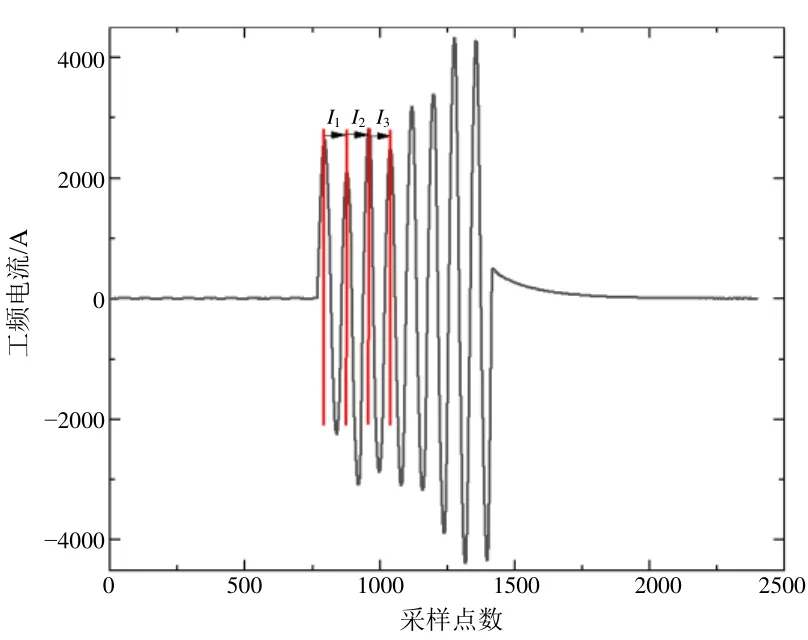
图5 故障工频增量保护触发逻辑示意图

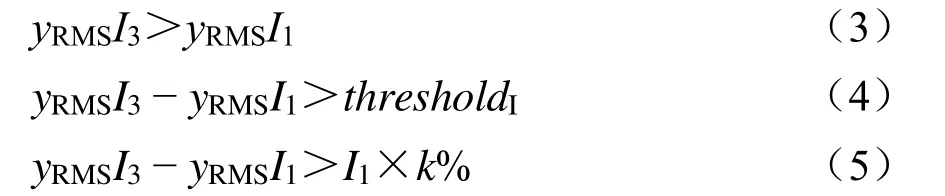
本次工频故障电流如图5所示，依据铁路接触网智能故障监测装置工频电流触发经验值，thresholdI= 287.3 A，k= 20。选取直供牵引所部分工频电流进行有效值计算，依据式（2）—式（5）对其进行故障判定，当计算数值满足时，则判定为故障跳闸，此后采用滤波后的高频信号（即行波信号）进行小波分解，从而实现直供方式下接触网线路故障精确定位[16～18]。

3 行波故障测距定位方法

当牵引供电系统发生振荡或故障跳闸时，接地点会产生向两边传播的行波电压，利用高精度GPS进行行波电压绝对时刻对时。应用于牵引供电系统的行波法故障精确定位是指当电力系统发生故障跳闸时，获取行波到达双端的波头时刻，利用对应的模量波速进行故障测距，其测距计算式为

式中：d为距离牵引所距离，L为两监测终端之间的距离，v为行波传播波速，t1为一端监测经相模变换后时刻，t2为另一端监测经相模变换后时刻。

进行故障定位时，在行波波速方面，利用被测线路参数进行相模变换，一般情况选用线模波速进行故障测距；在行波波头方面，结合 GPS获取行波的绝对时刻，然后利用小波变换获取行波到达双端传感器的波头时刻从而进行故障定位。

3.1 行波波速

行波是指行走的电磁波，在接触网线路中，行波会以电场和磁场相互变换的方式传播，在忽略接触网电路对地导纳后，传播的波动方程为

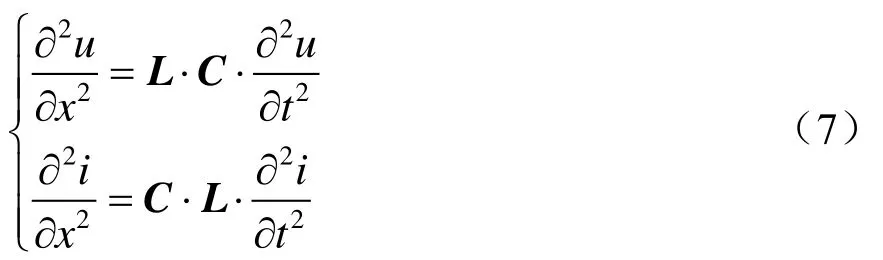
式中：∂u为故障点电压偏微分值；∂i为故障点电流偏微分值；∂x2为故障点距离平方的偏微分值；∂t2为行波传输时间平方的偏微分值；L为线路中不同相别的电感矩阵；C为线路中不同相别的电容矩阵[19]。

当线路固定时，L、C为固定参数。由此可见，行波的波动过程只与传输时间和传输距离有关，与线路本身无关。无论是输电线路还是牵引供电系统中，都存在耦合关系，电磁解耦后变成相互无关系的电磁关系模量，解耦方法大多采用对角阵法计算，通过解耦可知：

式中：Zm为各模量波阻抗；Vm为各模量波速度。

对于直供牵引供电系统，考虑到牵引供电系统一般采用上下行并联的方式运行，因此在进行直供线路故障定位时需考虑另一行接触网对本行的影响。直供线路等效模型如6所示。

通过图6中等效模型构建ATP-EMTP模型，建立回流线、钢轨、接触网3个等效参数，视钢轨为四分裂导线，承力索、接触网共同体为两分裂导线，回流线为两分裂导线，从而求取行波在接触网中线模波速度，通过解耦获取各直供接触网线路电容、电感矩阵，通过式（8）即可求取线模波速度。

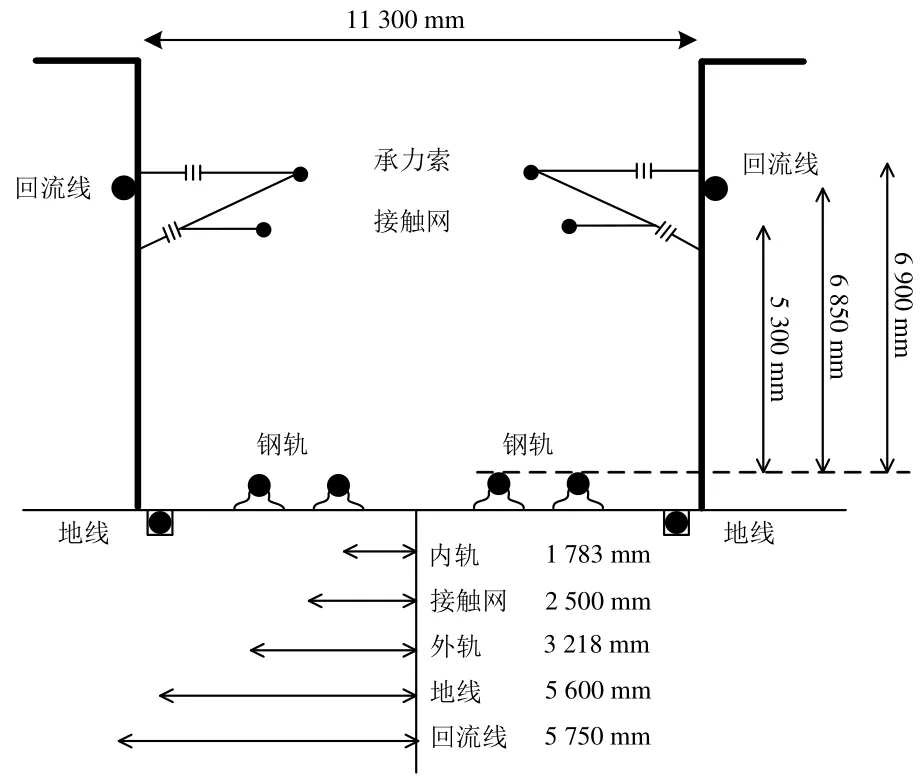
图6 直供系统上下行全并联等效模型

3.2 小波函数及分解层数的对比

小波变换是一种现行的极为有效的数据处理方法，常规的小波变换采用小波基函数及尺度函数进行。小波变换能够很好地实现信号在时域和频域的区分，但小波变换中存在多个小波基函数及尺度函数，针对同一个行波电压信号，采用不同的小波基函数及尺度函数可能出现不同的结果。理论上，监测装置采样率越高，小波尺度函数分解层数越大，最终故障定位越准确。但从实际工程应用层面上，过高的设备采样率影响数据传输时效，过高的分解层数可能导致系统响应较慢。结合上述考虑，非接触式传感器采用10 MHz的采样频率，选取db5、db8、sym5、sym8进行4、6、8、10层分解，结合经验法手动标记波头进行对比，图7所示为经验法标记牵引供电系统故障行波电压波头时刻，图8所示为不同小波尺度函数及分解层数误差对比。

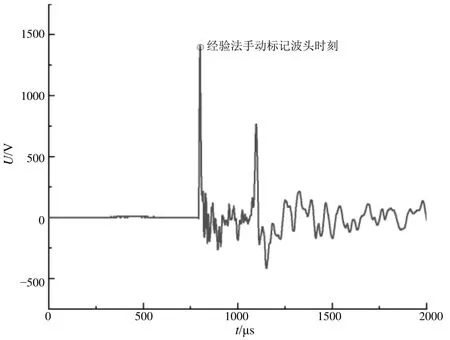
图7 经验法标记波头故障时刻

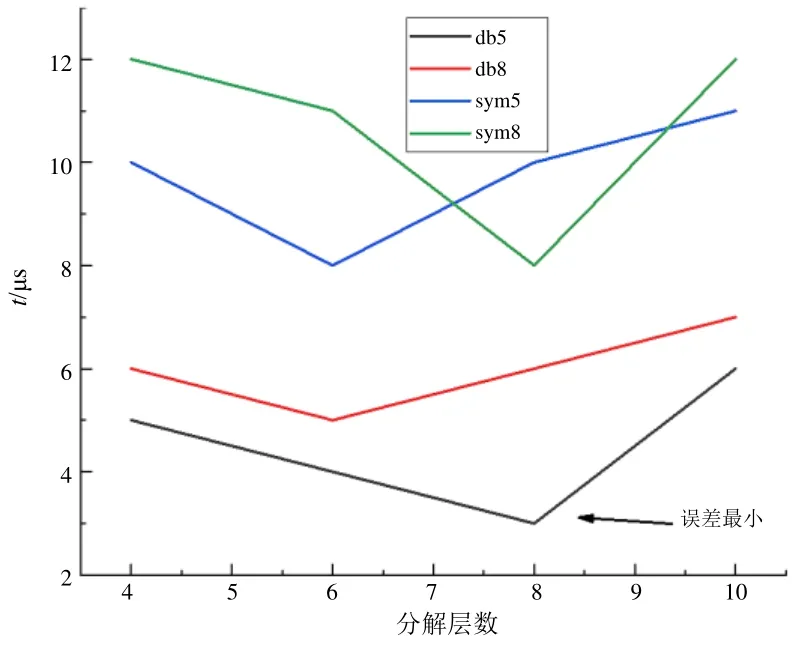
图8 小波变换及分解层数误差对比

经过多次试验，在利用小波变换时选取多种小波基函数及分解层数进行误差对比可知，采用小波函数db5进行8层分解时，此时故障测距偏差最小。下文对非接触式监测终端进行现场实验验证。

4 实验验证

4.1 实验概况

选取南宁局管内某直供线路进行故障测距验证，本直供线路采用上下行并联方式供电，部分区域设有加强线，牵引所上网点公里标（K243+209），分区所上网点公里标（K261+100），主线全长17.891 km，途经阳朔站和一个开闭所，开闭所中带绕行线，在 X牵引所处采用电缆架空上网，上网线全长约500 m。分别在牵引所和分区所上网点前支柱上安装非接触式故障监测装置，分别选取距离牵引所6 km处和距离牵引所10 km处进行短路接地实验。图9为接触网现场等效示意图。

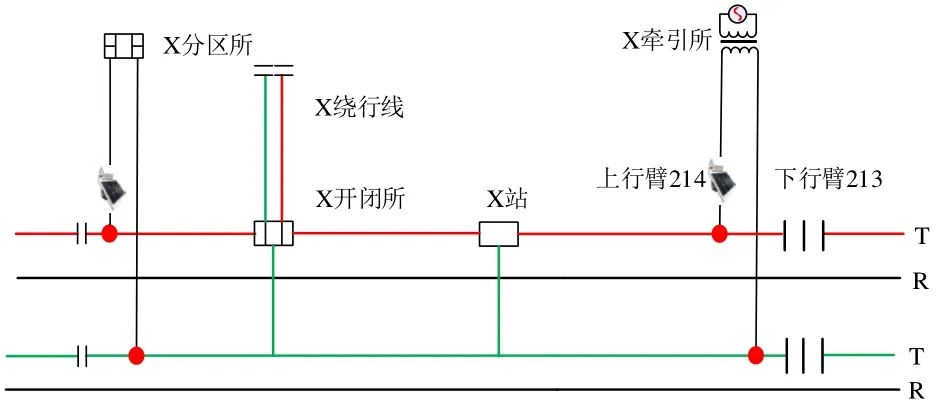
图9 现场供电示意图及装置安装点

由于该直供线路存在 T接绕行线及部分区域存在加强线，线路阻抗分布不均，采用阻抗法故障测距误差较大，甚至无法区分线路故障位于主线还是支线。选择采用非接触式故障测距，弥补所内故障测距判定精度过低的情况。在安装非接触式行波故障测距监测装置后，利用已知接触网参数进行相模变换，表1所示为经过相模变换后参数[20，21]。

表1 相模变换后各模量参数

由于接触网线路对地高度较小，线路对地杂散电容较大，而行波波速受到影响，选取不同的模量进行故障测距时，其故障定位结果相差较大。依据参考文献[18]中提及行波衰减和色散问题，在长距离输电情况下，行波波头和相位都会发生偏移，为保证应用于牵引供电故障测距系统的稳定性和有效性，本文选取接触网线模量波速作为故障测距参考波速，依据式（8）进行参考波速v计算：

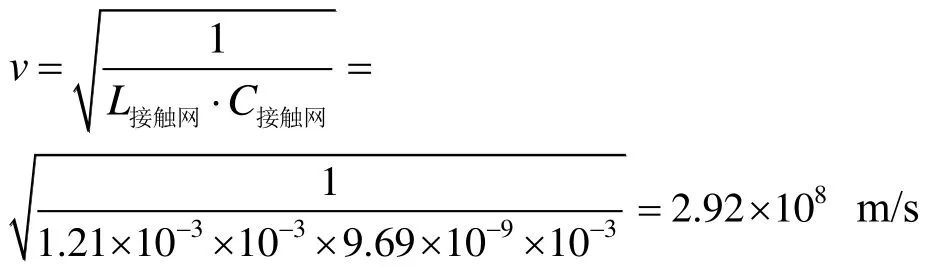
4.2 故障定位计算

为验证非接触式牵引供电故障测距装置的高精度性和稳定性，选取故障点距离牵引变电所6 km处进行金属性接地短路实验，接地电阻小于10 Ω，然后在变电所内进行合闸操作。非接触式牵引供电系统故障监测装置按图1所示流程进行故障判定，系统快速响应判定为故障跳闸，对牵引所、分区所采集的行波电压数据进行小波变换，电压行波模极大值判定为行波波头时刻，采用db5进行8层分解。图10所示为牵引所和分区所监测装置采集到的行波电压波形及其对应的小波变换结果。

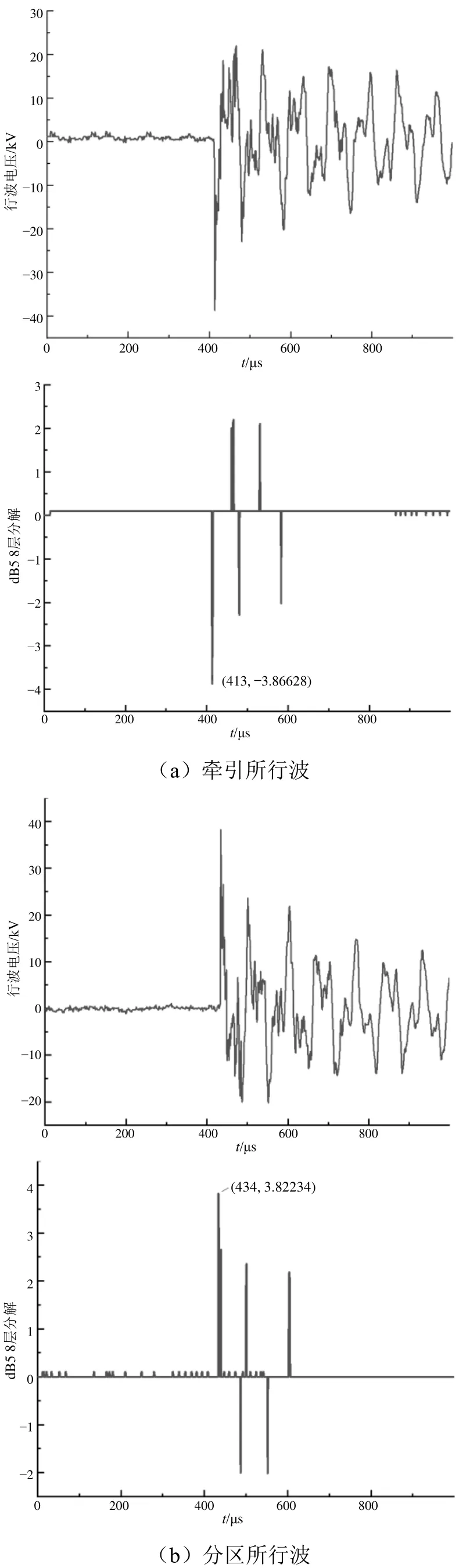
图10 短路实验行波电压及其小波变换结果

如图10所示，对牵引所、分区所的短路实验数据进行分析，利用最佳小波变换即db5 8层分解，得到的牵引所和分区所对应的模极大值即为波头故障时刻，即t1= 413 μs，t2= 434 μs。将相关数据代入式（6）可得出故障点距离牵引所距离为

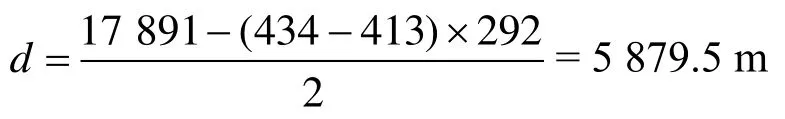
更换实验地点，采用上述相同方案进行故障实验，选取故障点距离牵引变电所10 km处进行高阻性接地短路实验，接地电阻约为1 000 Ω，验证非接触式故障监测系统在高阻抗情况下特性。在变电所断路器合闸后，对牵引所、分区所采集的行波电压数据进行故障测距计算，系统采集行波电压波形和小波变换结果如图11所示。

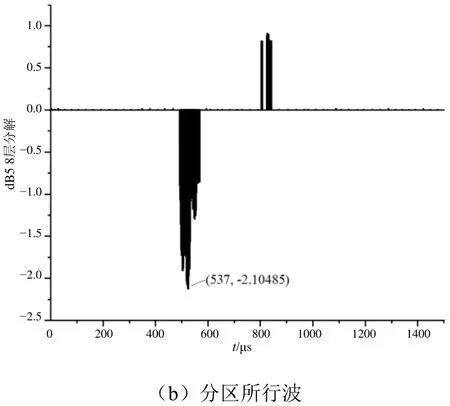
图11 高阻接地实验行波电压及其小波变换结果

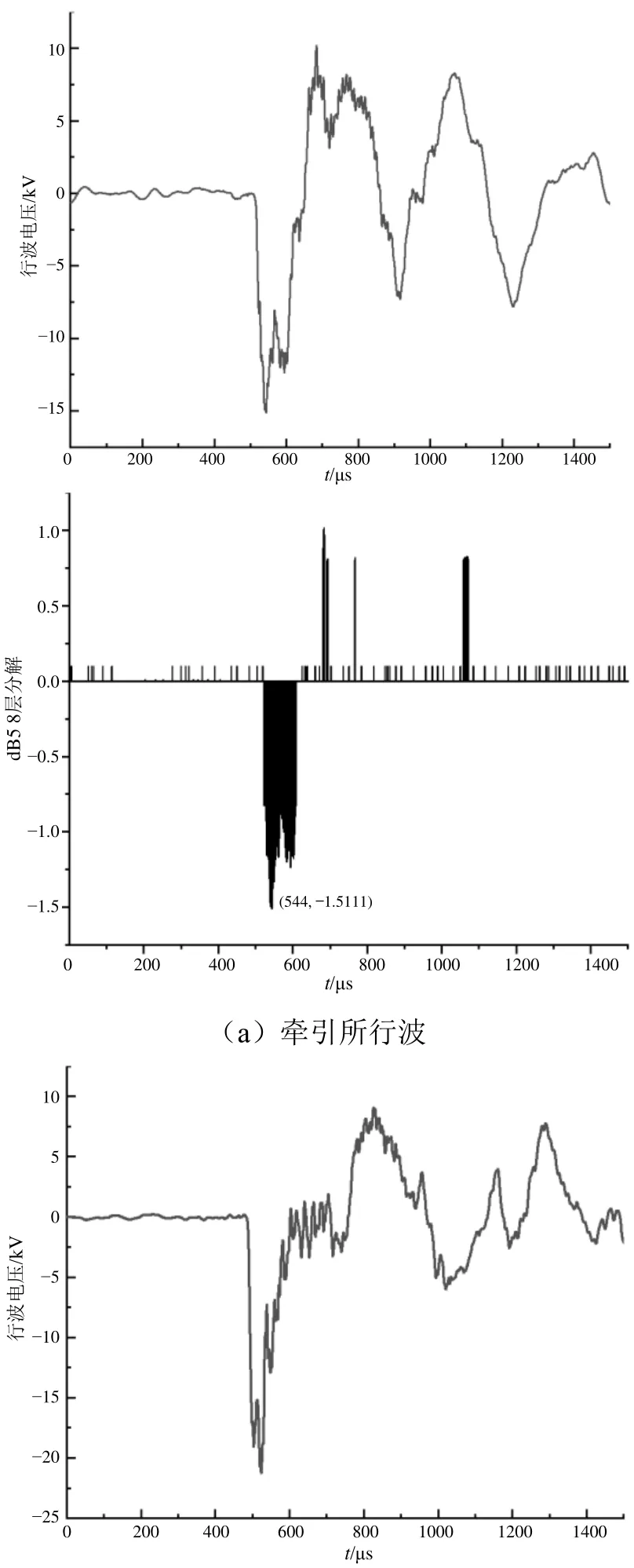
得到小波变换后的结果，通过对监测终端进行计算可得出高阻接地实验情况下故障点距离牵引变电所距离为

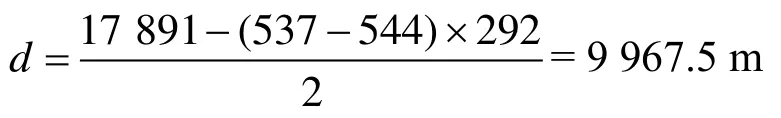
对非接触式故障监测系统进行不同距离和不同短路阻抗下故障测距精度验证，实验表明：非接触式故障监测终端不仅能实现直供接触网线路的信号测量，同时能够保证监测终端的故障快速启动和判定，且在线路存在加强线及T接绕行线的情况下，故障监测终端依然能保证200 m误差以内的故障测距精度，从而弥补了所内阻抗法故障测距的不足，具有重要的工程实际意义。