基于V型接线牵引变压器及SVG的同相供电方案研究
2023-01-11张一鸣解绍锋
张一鸣,解绍锋,王 辉
0 引言
自电气化铁路兴建以来,由于牵引供电系统所具有的特殊性,其电能质量问题始终为研究热点[1]。我国的电气化铁路广泛采用单相工频交流制供电方式,牵引负荷作为一种波动频繁且具有较强随机性的大功率单相电力负荷,其本质上具有单相独立性和不对称性,会在一定程度上破坏电力系统的三相平衡,从而导致大量的负序电流经由牵引变电所源源不断注入到公用电网中,进而可能对电力系统一次及二次设备的安全稳定运行产生影响[2]。
伴随着近年来铁路运量的不断增长,一方面采用PWM整流技术的交直交型电力机车得到大规模推广应用,相较于传统的交直型电力机车,其牵引功率提升巨大,使得负序问题愈加凸显。另一方面,由于交直交型电力机车与既有交直型电力机车混跑的情况在今后相当长一段时间内仍将继续存在,因此对于牵引负荷的功率因数问题也仍需考虑加以解决。
为了降低牵引负荷对公用电网造成的三相不平衡影响,现行的牵引供电系统往往采用牵引变压器轮换相序、分区供电的方案,并在分相以及分区供电处的接触网上设置电分相环节,以形成中性区用于实现相邻两供电臂之间的电气隔离。由于电力机车在过分相时受电弓无法平滑地从接触网受流,将直接导致机车牵引力损失,运行速度降低,以及运输能力受到限制,并同时伴随着过电压和过电流等一系列复杂的暂态机电过程,增大了设备故障和保护装置误动的风险,降低了供电系统的可靠性。电分相的存在不仅极大地制约了我国电气化铁路朝向高速和重载方向的发展趋势,同时也是现行牵引供电系统中最薄弱的环节[3,4]。
针对如何有效解决电气化铁路的电能质量及电分相问题,国外方面,德国通过建立铁路专用的发、输、配电系统而与公用电网进行隔离,同时对于接入公网的牵引变电所,在所内设置三相/单相旋转变流器,可以从源头上避免负序电流的产生,并能够取消大量电分相,实现牵引网全线贯通供电,但受到其供电制式的限制和巨大的投资建设成本,导致其难以进行大规模推广应用。日本“新干线”则通过在牵引变电所内广泛设置三相-两相平衡接线牵引变压器,并配合铁路功率调节器(Railway static Power Conditioner,RPC)实现功率融通及无功补偿,能够较好地解决电能质量问题,但电分相仍然存在。法国电气化铁路大量采用单相牵引变压器,通过在变电所内部加装三相静止无功发生器(Static Var Generator,SVG),以实现对系统三相不平衡等电能质量问题的治理[5,6]。国内方面,以西南交通大学李群湛教授为代表,率先提出了同相供电技术方案,并成功应用于成昆线眉山牵引变电所、山西中南部铁路通道、温州市域铁路S1线,以及广州地铁18号线和22号线等实际线路当中。大量的理论研究和工程实践结果表明,电气化铁路实施同相供电是改善电能质量并彻底取消电分相环节的最佳技术途径[7~10]。
鉴于近年来SVG有源无功型补偿技术在无功功率补偿、负序治理以及谐波抑制等方面所具有的突出性能和较高的性价比[11,12],本文针对我国电气化铁路中普遍应用 V型接线牵引变压器,提出一种基于单相SVG构建的新型同相供电系统方案,该方案的特点在于牵引供电与补偿设备可共用一台变压器。通过对所提方案的系统拓扑结构及综合补偿原理进行分析研究,构建负序无功综合补偿数学模型,确立综合补偿系统控制策略,最后通过搭建仿真模型,对所提系统方案的可行性及控制策略的有效性进行仿真验证。
1 基于V型接线牵引变压器及SVG构建的同相供电方案
牵引变压器的主要作用是将公用电网中的三相电变换为电力机车所使用的单相电,其中 V型接线牵引变压器相较于单相接线变压器在相同负荷条件下产生的负序功率更低,同时与YNd11接线以及三相-两相平衡接线变压器相比,具有结构简单、易于实施等优点。基于 V型接线牵引变压器,通过在其次边绕组构造牵引端口以及多个补偿端口,并利用SVG补偿装置对牵引负荷实施动态对称无功补偿,从而在确保电能质量满足要求的同时,还可在结构上取消牵引变电所出口处的电分相环节,实现同相供电。
图1所示为采用该方案的同相供电牵引变电所的拓扑结构示意图。变电所内部主要由牵引-补偿变压器(Traction Compensation Transformer,TCT),综合补偿装置(Comprehensive Compensation Equipment,CCE)以及综合补偿测控系统(Measurement and Control System,MCS)3个部分组成。

图1 同相供电牵引变电所拓扑结构示意图
TCT由一台次边绕组电压等级与容量均不相同的不等边 V型接线牵引变压器构建而成,其原边端子分别与公用电网的A、B、C三相高压母线连接,次边绕组ab和b′c由于采用不等边设计,绕组ab的电压等级将高于b′c,若认为绕组ab和b′c的线圈匝数分别为m和n,设置绕组ab为牵引端口时,以 a端子为基准,在牵引端口绕组匝数的2n处以及 3n处分别引出抽头d1和 d2,并将抽头d1与次边绕组b′c的b′端子相连后,即可分别构成3个无功补偿端口,即第1无功补偿端口ac、第2无功补偿端口d2c以及第3无功补偿端口ad1,此时第1无功补偿端口ac与第2无功补偿端口d2c将具有相同的电压等级,其大小为次边绕组b′c端口电压的倍,而第 3无功补偿端口 ad1的电压等级则将略大于另外两个无功补偿端口,且其大小为次边绕组b′c端口电压的2倍。TCT的原次边端口电压相量图如图2所示。
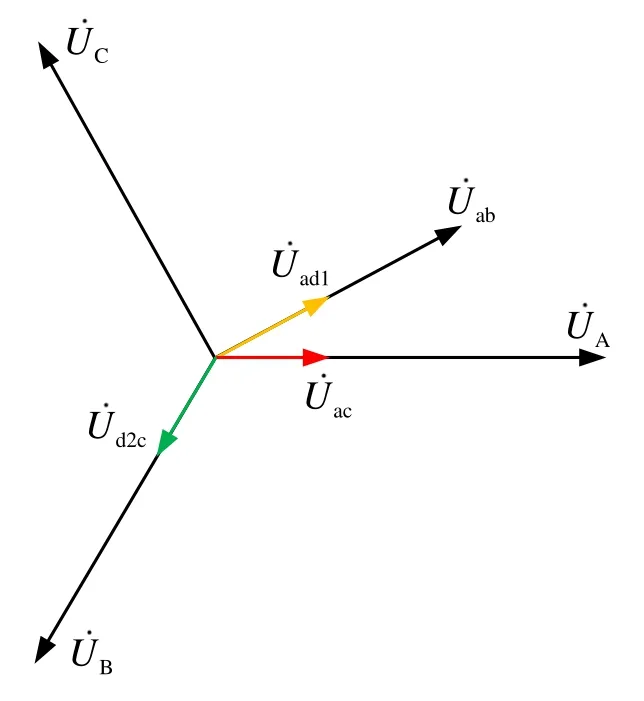
图2 TCT原次边端口电压相量示意图
与此同时,CCE所包含的3台单相SVG在正常运行时彼此之间相互配合,通过在各补偿端口发出特定大小和性质的无功功率,从而产生与系统负序功率方向相反的补偿分量,进而达到补偿目标,此时CCE只改变系统的无功潮流,而对系统的有功潮流并不会产生影响。
此外,MCS主要用于控制系统的正常运行,通过获取实时的负荷数据以及参数信息,并对相关数据进行判断和运算处理,从而控制CCE运行在相应的工作模式下,针对不同负荷的特点有选择地执行相应的补偿策略。MCS主要由电压互感器(Potential Transformer,PT)、电流互感器(Current Transformer,CT)以及控制器(Control Device,CD)构成。
2 补偿原理分析
根据文献[1]可知,对于TCT次边的任意牵引端口或补偿端口中所流过的单相电流,其在原边公用电网中所产生的总合成正、负序电流的通用表达式为
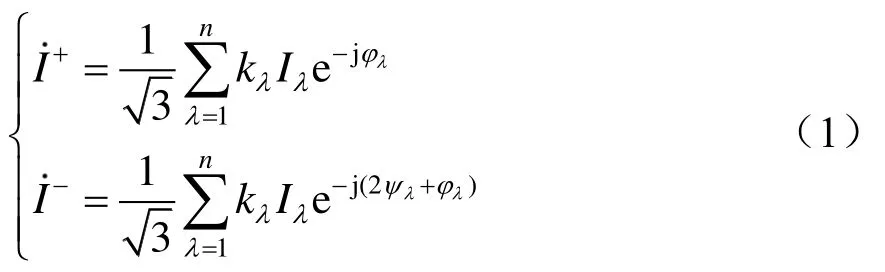
式中:n为牵引补偿变压器次边牵引端口和补偿端口的数量;kλ为牵引补偿变压器次边各端口电压与原边线电压之比,为端口电流的有效值;ψλ为端口电压滞后于A相电压的角度,也称为接线角;φλ为功率因数角(以滞后为正)。
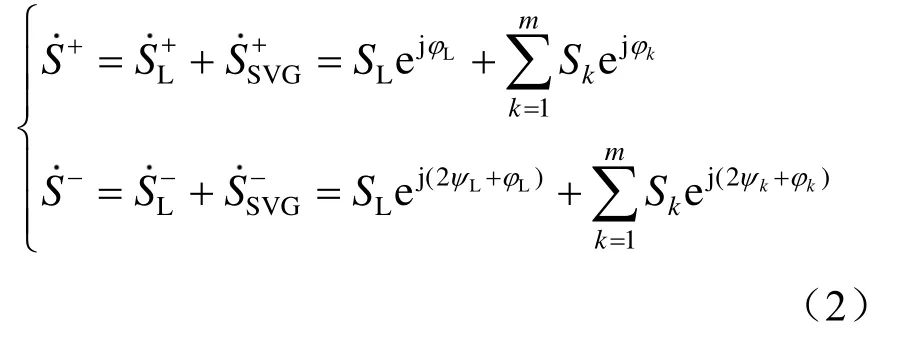
式中:SL为牵引端口功率,SSVG为补偿端品功率,Sk为第k个补偿端口功率,m为牵引补偿变压器次边补偿端口数量。
为了更好明确负序无功综合补偿的效果,可以通过定义负序补偿度KN和无功补偿度KC来进行约束,其中负序补偿度KN表达式为
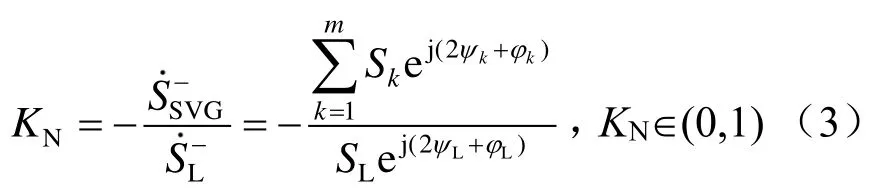
根据相关国标中对于相间单相负荷SL引起的负序电压不平衡度εU2的规定可知
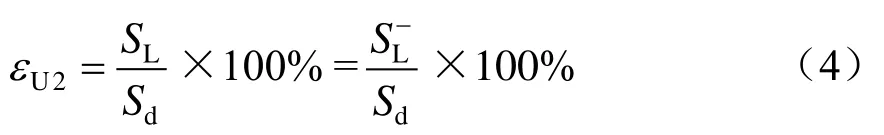
式中:Sd为系统短路容量。

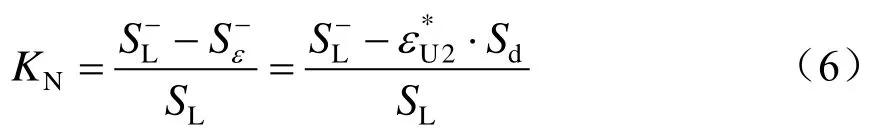
而对于无功补偿度KC,将式(2)中正序视在功率的表达式按照有功功率和无功功率的形式分别展开,则有

由式(7)便可得到
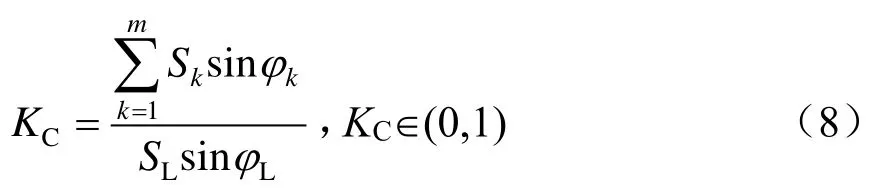

结合式(8)和式(9)还可以得到KC的另一种表示形式为
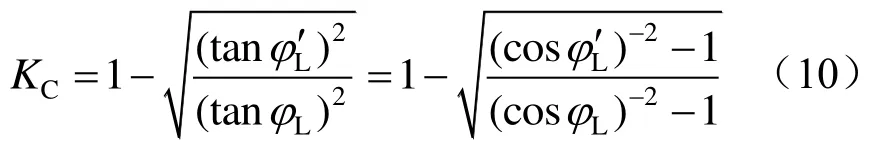
此时若将式(3)按照实部与虚部展开,并与式(8)进行联立,即可得到负序无功综合补偿的通用数学模型为
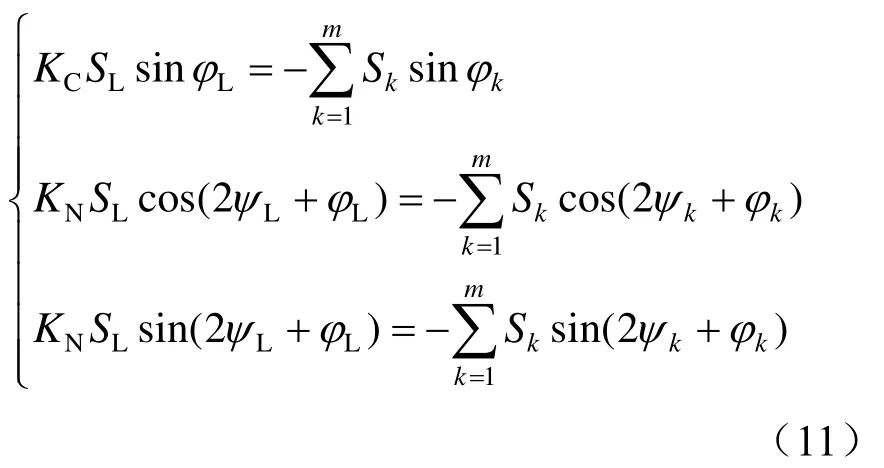
鉴于在实施补偿的过程中,根据牵引负荷的特点,可以分别考虑针对负序功率和无功功率同时进行补偿,或仅针对负序功率进行补偿,再或者仅针对无功功率进行补偿,因此对于CCE而言,可将其工作模式划分为3种情形,即负序无功综合补偿模式、负序补偿模式以及无功补偿模式。
2.1 负序无功综合补偿模式
负序无功综合补偿模式主要适用于牵引负荷产生的负序电流对公用电网造成的电压不平衡问题突出且负荷本身功率因数较低的场景。结合图1和图2可知,系统正常运行时,CCE中的SVG1、SVG2以及SVG3均投入运行,若以A相电压为基准,则牵引端口与各补偿端口的接线角可分别表示为:ψL= -π/6,ψ1= 0,ψ2= 2π/3,ψ3= -π/6;并且当认为SVG1为感性补偿,SVG2和SVG3为容性补偿时,则由式(11)可得到所提系统方案的综合补偿模型为

对式(12)进行联立求解,即可得到 SVG1、SVG2以及SVG3在实现负序无功综合补偿时所应发出的无功功率的理论计算通式为
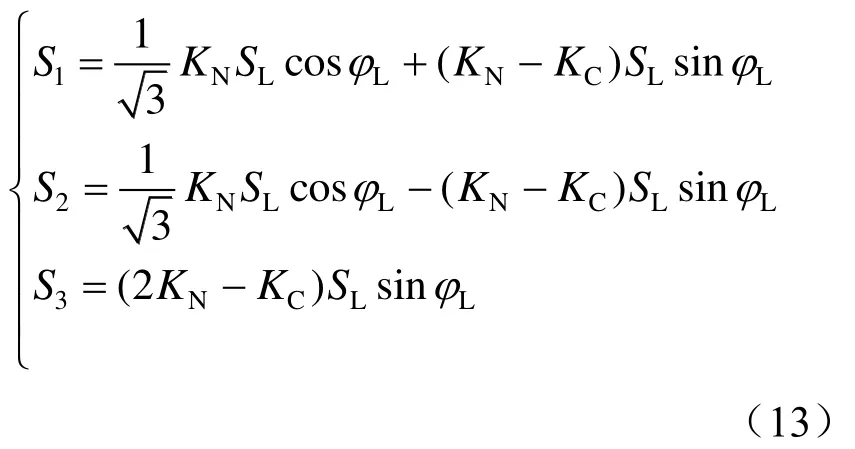
若进一步将式(12)除以牵引端口电压UL,则还可以得到SVG1、SVG2以及SVG3在各自的补偿端口处应输出的补偿电流为
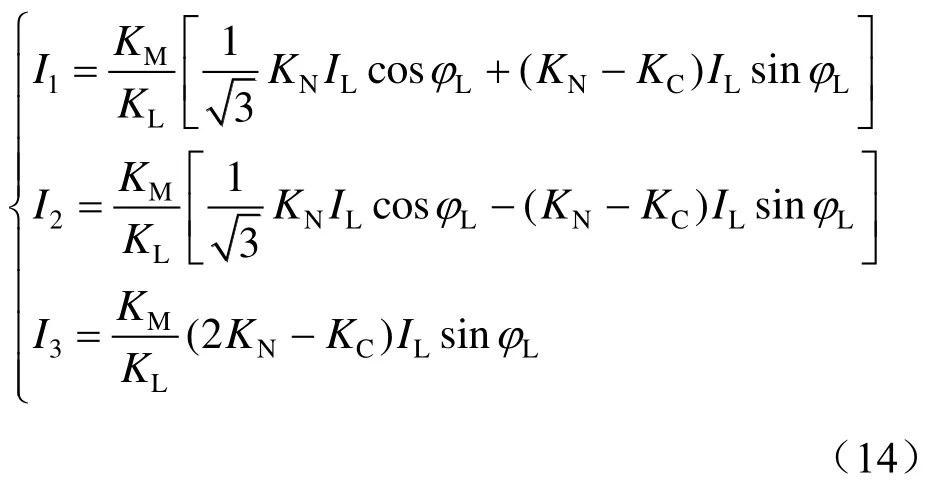
式中:IL为牵引负荷电流;KL为TCT牵引端口的变比,KL=UA/UL;KM为补偿端口的变比,KM=UA/Uk(k= 1,2,3)。
因此当考虑实施负序无功完全补偿时(即负序补偿度KN= 1,无功补偿度KC=1),根据式(1)和式(14),可以作出负序无功综合补偿模式下的补偿原理相量图,如图3所示。
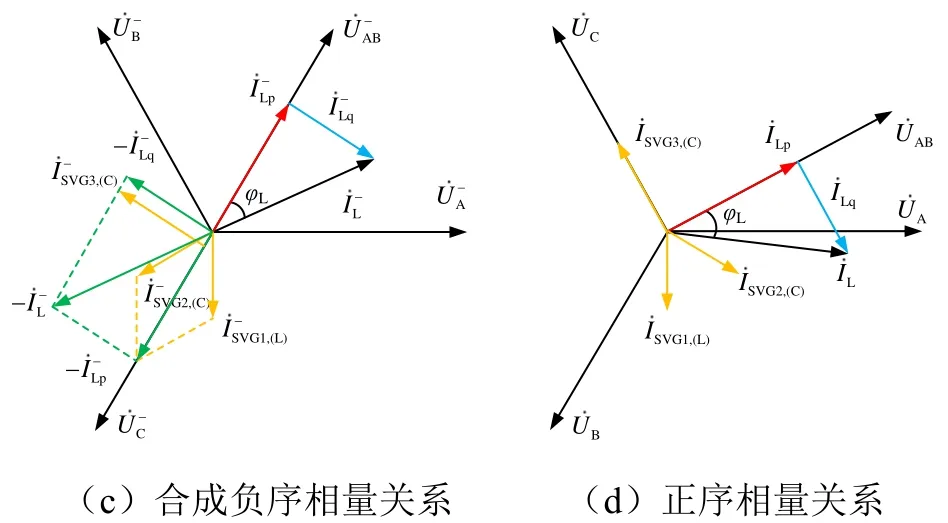
图3 负序无功综合补偿模式原理相量图
将牵引负荷电流按照有功与无功分量的形式分解,针对有功分量所产生的负序电流,通过利用SVG1与SVG2发出大小相等的感性补偿电流和容性补偿电流,经叠加合成后可实现对的抵消;而针对无功分量所产生的负序电流,则由SVG3发出与大小相等,方向相反的容性补偿电流以实现相互抵消。因此由SVG1、SVG2以及SVG3所产生的补偿电流合成量将与共线反向,从而能够实现对负序电流的对称补偿,同时三者注入系统的总无功功率也能够实现对牵引负荷正序无功分量的完全补偿。
2.2 负序补偿模式
负序补偿模式主要适用于牵引负荷产生的负序电流对公用电网造成电压不平衡问题突出,但负荷本身功率因数尚且满足要求的场景。当考虑对负序实施完全补偿时(即负序补偿度KN= 1,无功补偿度KC= 0),根据式(1)和式(14),可以作出负序补偿模式下的补偿原理相量图,如图4所示。
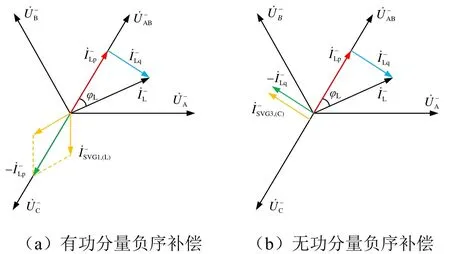

图4 负序补偿模式原理相量图
同理,仍可通过利用SVG1与SVG2发出大小相等的感性补偿电流和容性补偿电流实现对的抵消,但与负序无功综合补偿模式相比,区别在于针对的补偿,则需由SVG1和 SVG2进一步发出大小为的感性补偿电流和,并与 SVG3所发出的大小为的容性补偿电流相叠加合成,以实现对的抵消,从而实现对负序电流的对称补偿。另一方面,由于三者注入系统的总无功功率之和为零,因此补偿前后系统的功率因数不会发生变化。
2.3 无功补偿模式
无功补偿模式主要适用于牵引负荷本身功率因数偏低,但产生的负序电流对公用电网造成的电压不平衡问题尚且在允许范围内的场景。当考虑对无功实施完全补偿时(即负序补偿度KN= 0,无功补偿度KC= 1),根据式(1)和式(14),可以作出无功补偿模式下的补偿原理相量图,如图5所示。
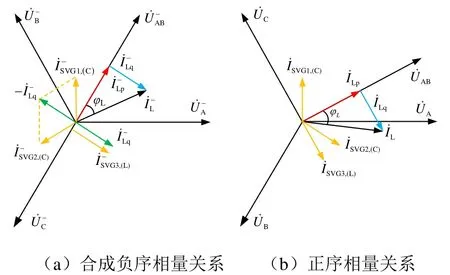
图5 无功补偿模式原理相量图
若以TCT原边A相电压为基准,设其电压瞬时值uA(t) =UAsin(ωt),则TCT次边牵引端口的端口电压uL(t)和负荷电流iL(t)的表达式可分别列写为
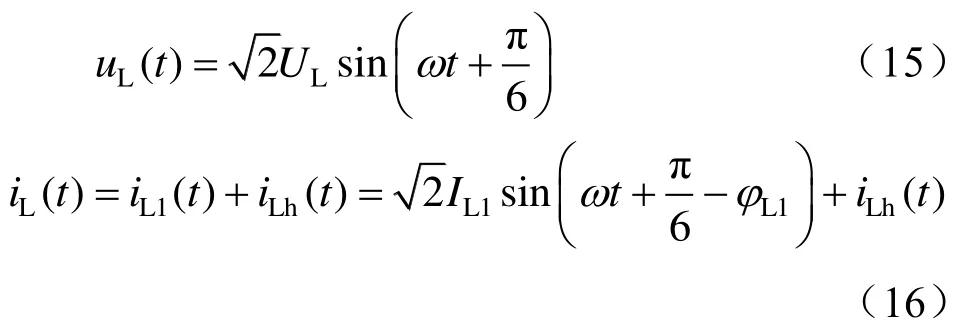
式中:iL1(t)为负荷电流iL(t)的基波分量,iLh(t)为负荷电流iL(t)的谐波分量。
若将式(16)中iL(t)的基波电流分量iL1(t)按照瞬时有功电流iLp(t)和瞬时无功电流iLq(t)的形式分解,则有

式中:ILp=IL1cosφL1,ILq=IL1sinφL1。
根据鉴相法原理,通过利用锁相环 PLL获取牵引端口电压uL(t)的同步电压信号sin(ωt +π/6)以及cos(ωt +π/6),并将其分别与式(17)相乘,则可以得到
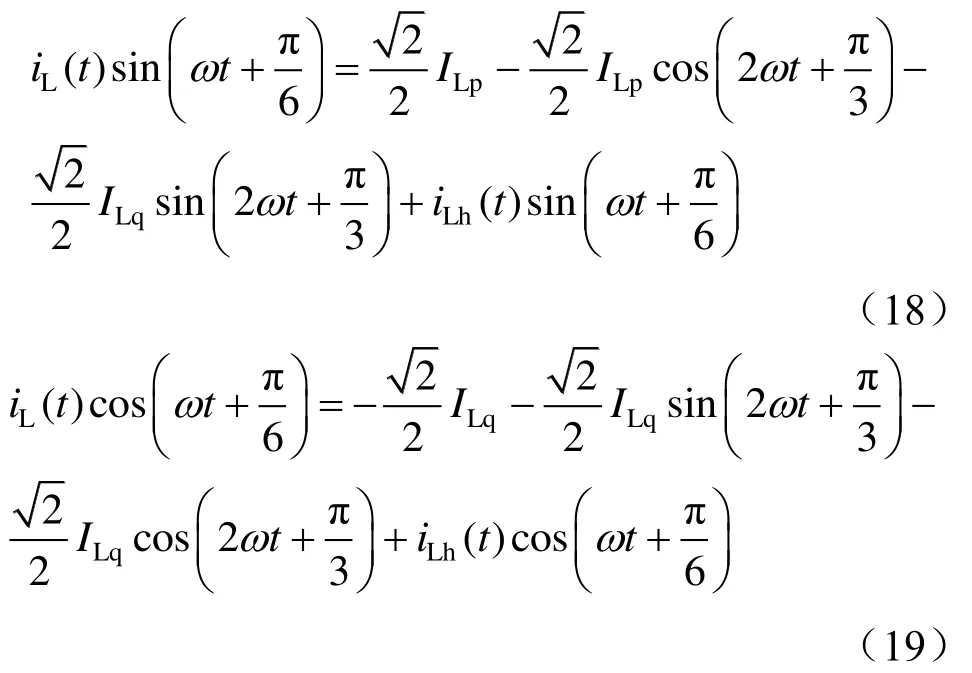
此时将式(18)和式(19)中的两组信号通过低通滤波器 LPF滤波并乘以二倍增益后,即可分离得到负荷电流iL(t)中基波瞬时有功电流的幅值,以及基波瞬时无功电流的幅值。
为得到期望补偿电流的参考信号,还需利用锁相环PLL分别针对各补偿端口的端口电压u1(t)、u2(t)以及u3(t)进行锁相,获取相应的同步信号即sin(ωt)、sin(ωt- 2π/3)、sin(ωt+ π/6),由于在牵引工况下,SVG1为感性补偿,SVG2和SVG3均为容性补偿,因此与之相对应的同步信号分别为-cos(ωt)、cos(ωt- 2π/3)、cos(ωt+ π/6),故由式(14)可以最终得到SVG补偿装置在各自的补偿端口应发出的期望补偿电流的参考信号为
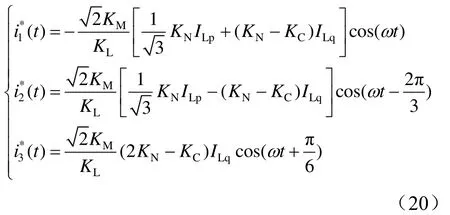
由式(20)可以绘制出期望补偿电流的检测原理框图,如图6所示。
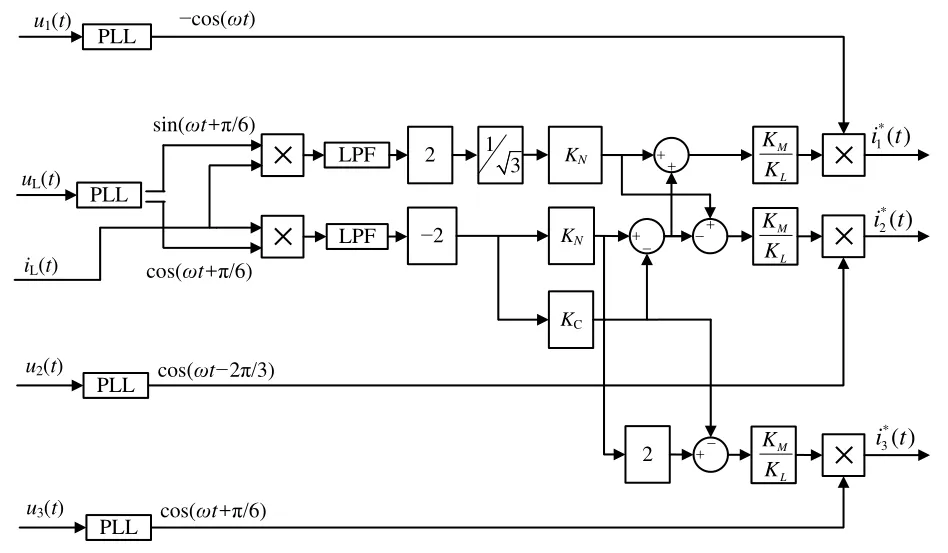
图6 期望补偿电流检测原理框图
根据计算得到的期望补偿电流参考信号,在对SVG实际的补偿电流输出值进行跟踪调制的过程中,还需同时考虑直流侧支撑电容的稳压控制,通过设置相应的直流电压参考值、以及,并将其与实际的直流侧电压Udc1、Udc2以及Udc3进行比较,经由PI调节后与各补偿端口的同步信号相乘,再将其并入交流侧补偿电流输出值的闭环控制中,并通过利用SPWM载波调制技术将计算得到的修正信号与三角载波进行比较,最终即可产生驱动SVG补偿装置的PWM控制信号,由此可以绘制出SVG补偿装置的控制策略原理框图,如图7所示。
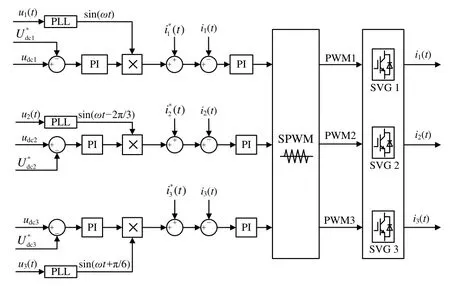
图7 SVG控制策略原理框图
4 仿真分析
为进一步对本文所述方案及系统控制策略的有效性和可行性进行验证,利用 Matlab/Simulink仿真平台搭建仿真模型,并基于某电气化铁路牵引变电所的实测负荷数据选取3个典型仿真工况,针对3种补偿模式的实际补偿效果进行仿真分析。其中外部电源的系统短路容量为500 MV·A,TCT原边进线电压等级为 110 kV,次边牵引端口额定电压为27.5 kV。
4.1 仿真工况一
设定牵引端口负荷功率为18.10 MV·A,功率因数为0.80,当采用负序无功综合补偿模式,对系统的负序及无功功率实施完全补偿时,其仿真典型值统计结果如表1所示,波形如图8所示。

表1 仿真工况一典型值统计结果

图8 负序无功综合补偿模式仿真结果(工况一)
在实施补偿前系统侧的三相电流波形存在明显的不对称现象,当仿真至0.2 s时,CCE投入运行,且在一个电流周期内便可基本达到稳定运行状态,在实施补偿后系统的三相电流波形接近平衡,三相电压不平衡度从补偿前的3.62%降低至0.00%,功率因数也从补偿前的 0.80提升至 1.00,达到了预期的补偿目标。
4.2 仿真工况二
设定牵引端口负荷功率为14.40 MV·A,功率因数为0.90,当采用负序补偿模式,对系统的负序功率实施完全补偿时,其仿真典型值统计结果如表2所示,波形如图9所示。在实施补偿后,系统的三相电流波形接近平衡,三相电压不平衡度从补偿前的2.89%降低至0.00%,但系统功率因数并未发生改变,能够达到负序补偿模式预期的补偿目标。
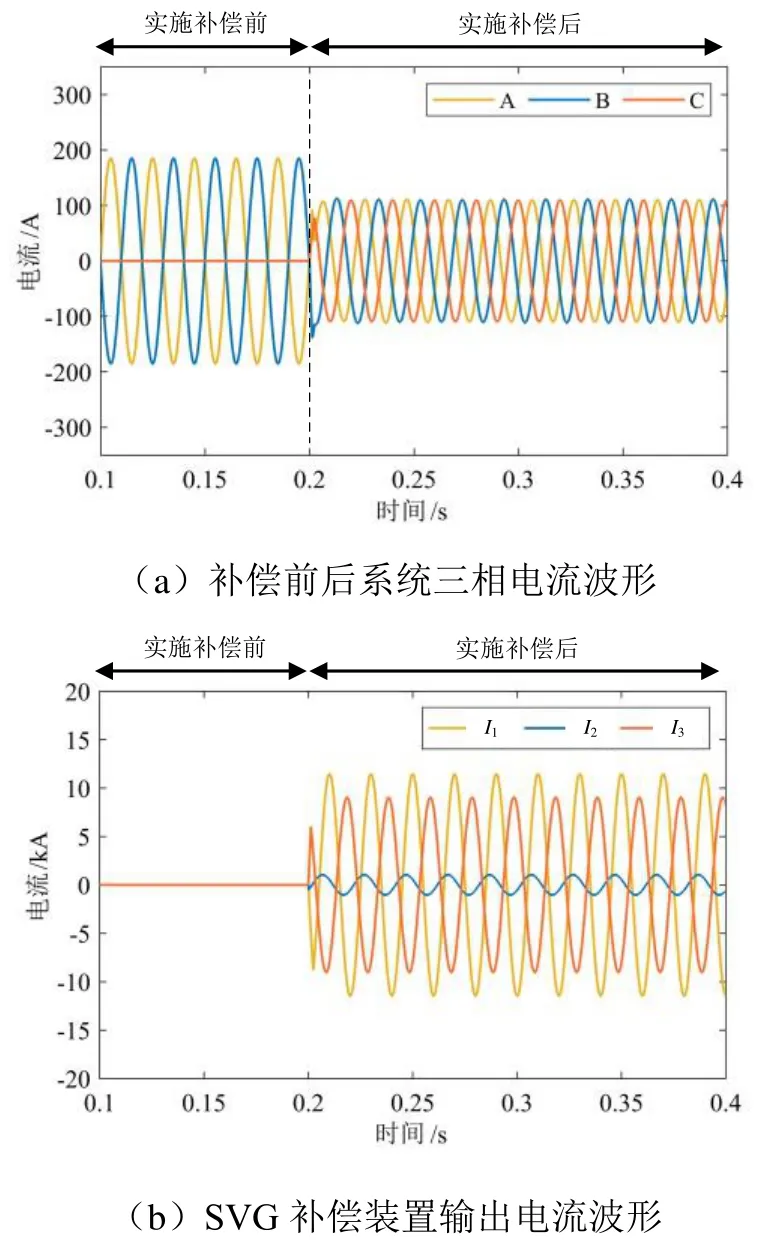
图9 负序补偿模式仿真结果(工况二)

表2 仿真工况二典型值统计结果
4.3 仿真工况三
设定牵引端口负荷功率为4.00 MV·A,功率因数为0.80,当采用无功补偿模式,对系统的无功功率实施完全补偿时,其仿真典型值统计结果如表3所示,波形如图10所示。在实施补偿后系统的功率因数从补偿前的 0.80提升至 1.00,但补偿前后系统的三相电压不平衡度始终维持在 0.80%的较低水平,无需对负序功率进一步补偿,达到了无功补偿模式预期的补偿目标。

表3 仿真工况三典型值统计结果
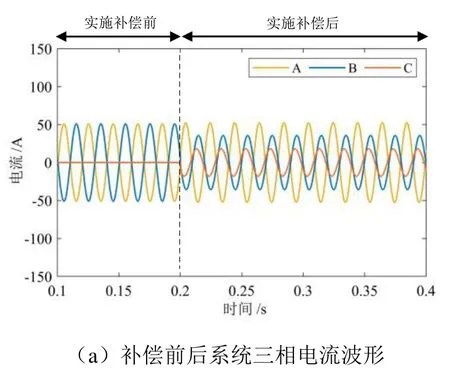
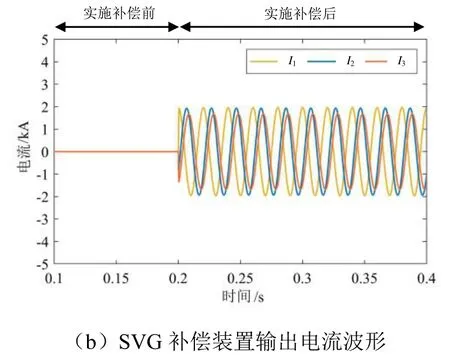
图10 无功补偿模式仿真结果(工况三)
综上所述,通过以上3个仿真实验结果,充分验证了本文所述方案及综合补偿控制策略的有效性,且系统响应速度较快,补偿效果较好。
5 结论
针对电气化铁路的电能质量及电分相问题,本文提出一种基于V型接线牵引变压器及SVG构建的同相供电方案,通过理论分析及仿真验证,得到以下结论:
(1)所述方案可取消牵引变电所出口处的电分相,实现同相供电,有利于减少列车过分相所产生的不良影响,提高列车运行安全性,同时能够有效解决以负序为主的电能质量问题。
(2)所述方案中TCT同时具有牵引端口与补偿端口,且二者之间可以进行绕组共用,集成度高,能够实现牵引变压器与补偿变压器的结构优化配置,有利于减少供电设备数量及牵引变电所占地面积,节省投资及运营维护成本。
(3)仿真结果表明,所述综合补偿方案有效可行,系统控制策略准确稳定,且SVG补偿装置工况可逆,运行范围灵活,能够广泛适用于不同负荷情形下的电能质量治理。
