基于Alpha-stable的粒子群算法变异策略研究及气动优化应用

樊华羽,李典,郝海兵,梁益华

(中国航空工业集团西安航空计算技术研究所,陕西 西安 710065)

航空科学技术的快速发展对飞行器气动力优化设计技术提出了更高的需求。借助各种优化算法，可以实现翼型、翼身组合体甚至全机减阻降噪设计与分析，为各种新型的飞行器研制提供支撑。

气动力优化设计[1]的关键技术之一就是优化算法。根据优化机制和行为的不同，这些优化算法可以分为两类：经典优化算法和智能优化算法。相比之下，以粒子群算法(particle swarm optimization,PSO)[2]和差分演化算法(differential evolution algorithm,DE)[3]为代表的智能优化算法由于良好的并行效率、全局性以及鲁棒性，得到了更多的关注。其中，PSO算法简洁易行、参数少、优化能力强，是气动优化领域广泛使用的算法之一。然而，该算法依然存在固有的缺陷，在进化后期，算法侧重于开采能力，容易陷入局部极值点，收敛速度慢，精度较差。为此，研究人员进行了一系列的研究工作并相继提出了多个改进的PSO算法。文献[4]针对PSO算法容易陷入早熟的缺点，对PSO算法引入田口算法思想，进行多目标优化，取得较好效果，但其是对单波束和半功率宽度进行优化，而没有用在多波束赋形方向，且该算法优化目标数较少。魏法等[5]从自适应操作粒子结构以及采用反梯度加权的方式平衡粒子群优化算法的全局搜索与局部搜索能力，通过对阵列相位、幅度优化实现低旁瓣、窄波束宽度和高增益效果。明振兴等[6]通过粒子群算法中的惯性权重线性化，使用余弦函数改进算法中的学习因子，使算法能够兼顾全局与局部寻优性能，并将改进后的粒子群算法应用于LED光源阵列的优化。周飞红[7]对粒子群算法引入爆炸因子，让粒子群能够通过爆炸的方式增强搜索能力，有利于算法跳出局部最优解，提高算法的搜索能力。李真等[8]将粒子群优化算法结合灰狼算法，根据自然界中的优胜劣汰法则，对每代种群中的最差粒子进行进化，提高粒子群算法的优化性能。综上所述，无论何种改进的PSO算法，出发点都是如何在提高算法收敛速度的同时提高全局收敛性，避免算法陷入局部最优，但是这些算法的调参方法和应用能力各有优劣。

本文针对飞行器气动优化设计中广泛使用的PSO算法的不足之处开展改进研究。在综合分析各种改进算法的基础上，提出了一种基于Alpha-stable动态变异的新型粒子群优化算法，使用多个测试函数对该算法的低、中、高维设计变量下的寻优能力进行了分析，最终将其应用到实际的气动优化领域，分析研究了RAE2822二维翼型的减阻设计。

1 基于Alpha-stable变异的粒子群算法

在粒子群优化算法中，粒子通过(1)～(2)式来更新自己的位置与速度。

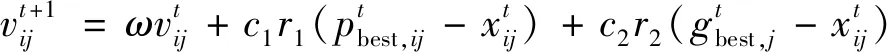
(1)

(2)

式中:i=1,2,…,N;j=1,2,…,n;x表示粒子所在位置;v表示粒子速度；ω为惯性权重因子，是一个在[0.4,0.9]之间动态变化的参数，它决定了粒子继承当前速度的程度，常见的动态变化策略主要有线性递减与线性微分等；c1,c2为学习因子，主要用来调节粒子群步长的参数；r1,r2为(0,1)之间的随机数；下标i和j表示第i个粒子和第j维；上标t为进化代数。

1.1 Alpha-stable分布的概率密度函数

概率密度函数是常用且极为重要的表示函数分布的工具，图像中一般表现为尾端趋近于幂律分布，头端偏离幂律分布。由于Alpha-stable分布的概率密度函数是存在且连续的，所以可以用Alpha-stable分布的特征函数的连续傅里叶变换来定义

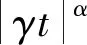
(3)

式中:sign(t)是t的符号;φ表示为

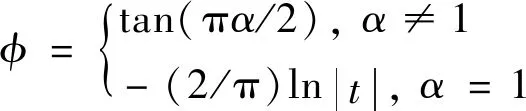
(4)

在Alpha stable分布中有3个特例:

1) 当α=2,β=0时，表示高斯分布，其概率密度函数为

2) 当α=1,β=0时表示柯西分布，其概率密度函数为

3) 当α=0.5,β=1时表示Levy分布，其概率密度函数为

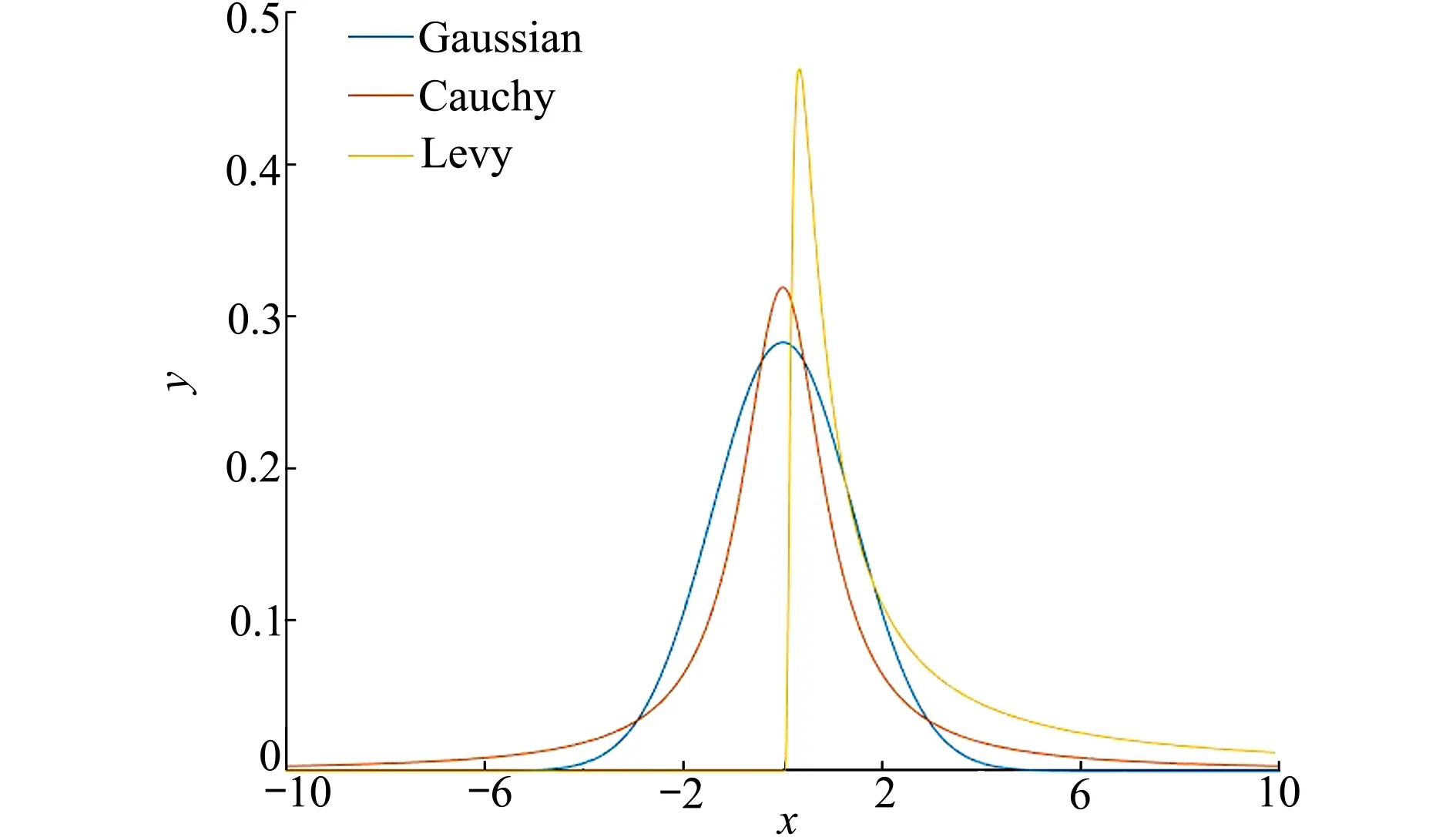
图1 高斯分布、柯西分布和Levy分布的概率密度函数图

除了高斯分布、柯西分布分布Levy分布以外，一般的稳定密度函数没有已知的封闭表达式，且其他任何稳定分布的密度函数都不太可能有封闭表达式。Zolotarev的研究表明[9]，仅在极少数情况下，可以用某些特殊函数表示。

将Alpha-stable分布X∈Sα(0,1,0)在α∈(0,2]内选择6个不同的α得到如图2所示的变化图。此时β=0，密度函数呈现关于0的对称分布。

在Alpha-stable分布中，图2a)呈现出钟型的对称稳定分布，可以看出当α减小时，函数图形会呈现3种变化：峰值变高、峰值两侧的区域变低、尾部变重。在图2b)中可以了解当α减小时尾部概率是如何增加的。通过改变稳定性系数α的大小，就可以改变成不同的Alpha-stable分布。

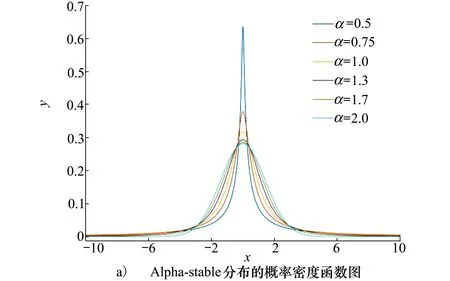
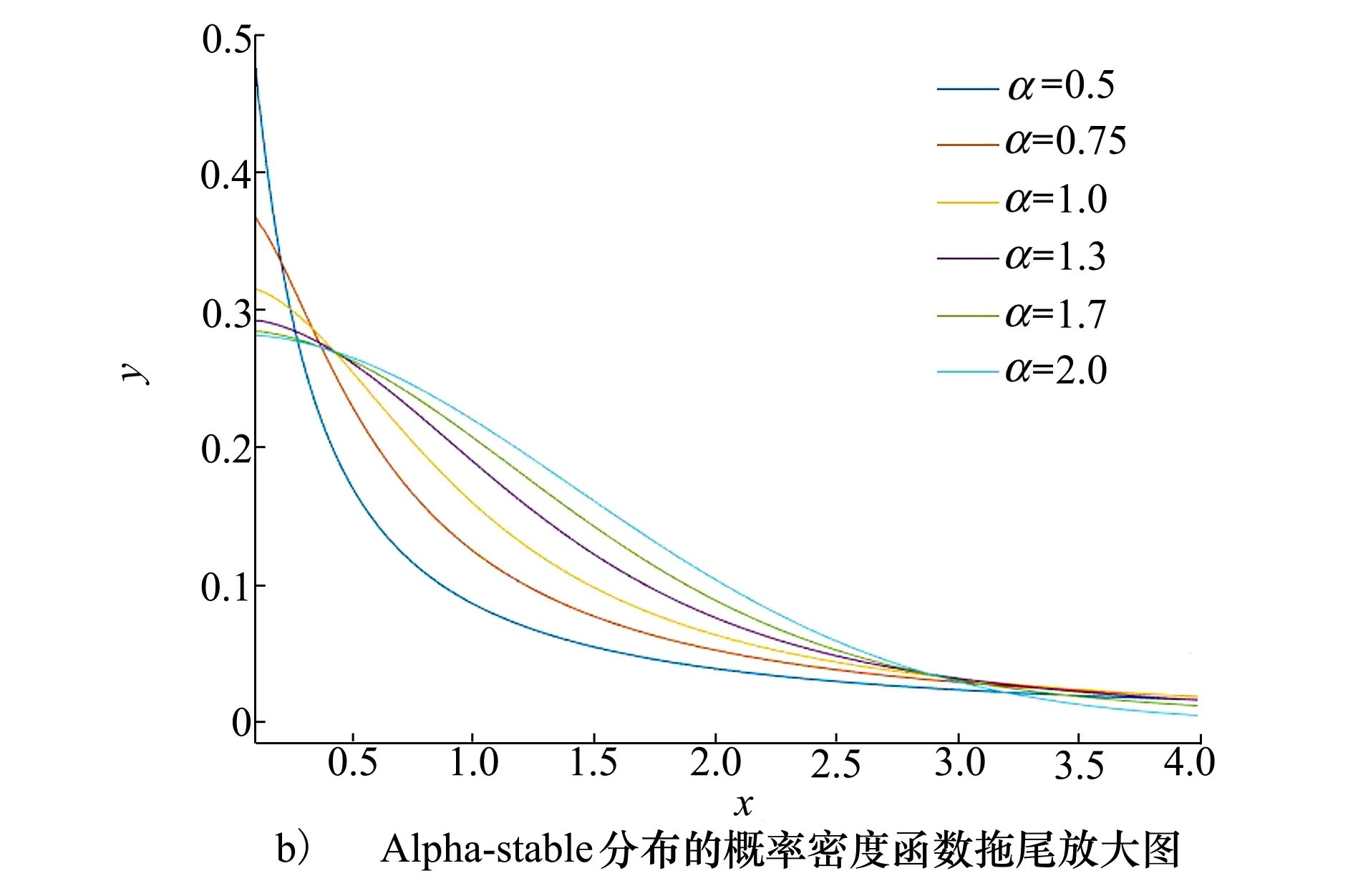
图2 函数图

1.2 稳定性系数α的变化策略与分析

由于粒子群算法容易陷入局部最优，通常在粒子群算法中加入一个确定的变异因子以避免过早陷入局部最优。本文选择通过Alpha-stable分布产生的随机数对粒子群算法中的个体进行变异操作。不同的稳定性系数α的变化过程决定不同的变异策略，本节通过测试函数来验证3种不同的变异策略下ASPSO优化算法的寻优能力。设置1为前期加速的上凸二阶函数型变异策略，设置2为无加速一阶函数型变异策略，设置3为后期加速的下凹二阶函数型变异策略，3种不同的变异策略趋势见图3。

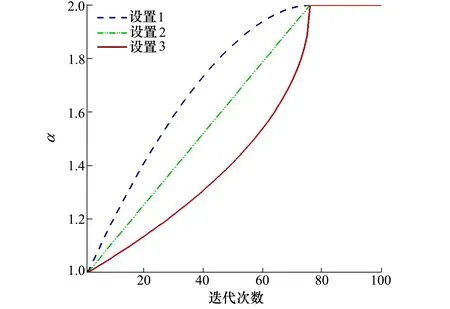
图3 不同设置的Alpha变化策略

通过7种标准测试函数在30维下的函数测试结果来比较哪种变异策略更具有优势。算法的种群规模均取100。惯性权重在[0.4,0.9]之间随代数线性递减。稳定性系数α的取值从1增加到2。所有算法的加速常数c1=c2=15。分别用3种算法搜索运行30次，每次运行迭代1 000次，统计30次优化的平均目标函数值和搜索到的最小目标函数值。

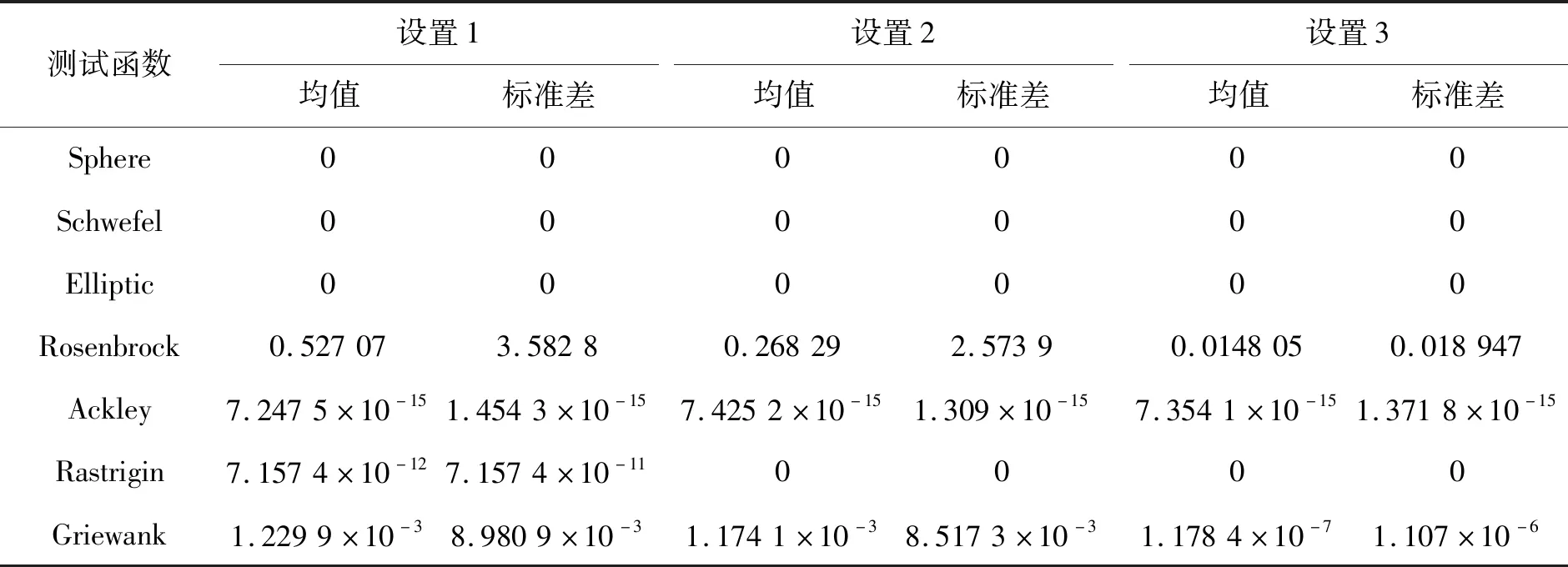
表1 不同变化策略下的测试函数结果对比

通过表1可以看出3种设置下的Alpha变化策略对粒子群优化算法的影响。一开始都是使用较小的α值，此时的变异方式为柯西变异，此种变异方式能够帮助提高粒子群优化算法的全局搜索能力，随着α值逐渐增大到2，变异方式也从柯西变异变化为传统的高斯变异，此种变异方式能够提高算法末期的搜索精度。那么表1中可以明确看出在设置1与设置2下，由于α值的增速过大，Alpha-stable变异过快地从柯西变异过渡为高斯变异，即过快地从寻找全局最优转换为局部寻优，不能较为优秀地帮助粒子群完成优化任务。总的来说，3种不同的设置方式下都能够得到较优秀的测试结果。其中测试结果差异较大的函数为Rosenbrock函数和Griewank函数。Rosenbrock函数是病态的，在极值周围梯度极小。Griewank函数是典型的非线性多模态函数，具有大量的局部极小值点。正是因为这2个函数本身的特点，对较为激进的变异策略较敏感，使得设置1和设置2情况下的测试结果没有设置3的数值优秀。设置3的变异策略在开始阶段使用较小的α值，采用变异能力较强的柯西变异增强了粒子群算法在初始阶段的的全局搜索能力，避免陷入局部最优；随着算法进程α值逐渐增大，最终增大为2，此时的变异方式为传统的高斯变异，提升算法末期的局部搜索能力，增强算法的搜索精度。通过动态调整Alpha-stable函数的稳定性系数α，完成变异范围以及幅度的变化，从而使优化算法能在搜索最优解时具有更好的精度以及全局搜索能力。最终选择设置3作为本文优化算法中的变异策略，稳定性系数α的变化过程见图4，本文命名在此变异策略下的粒子群算法为基于Alpha-stable分布的粒子群算法(ASPSO)。

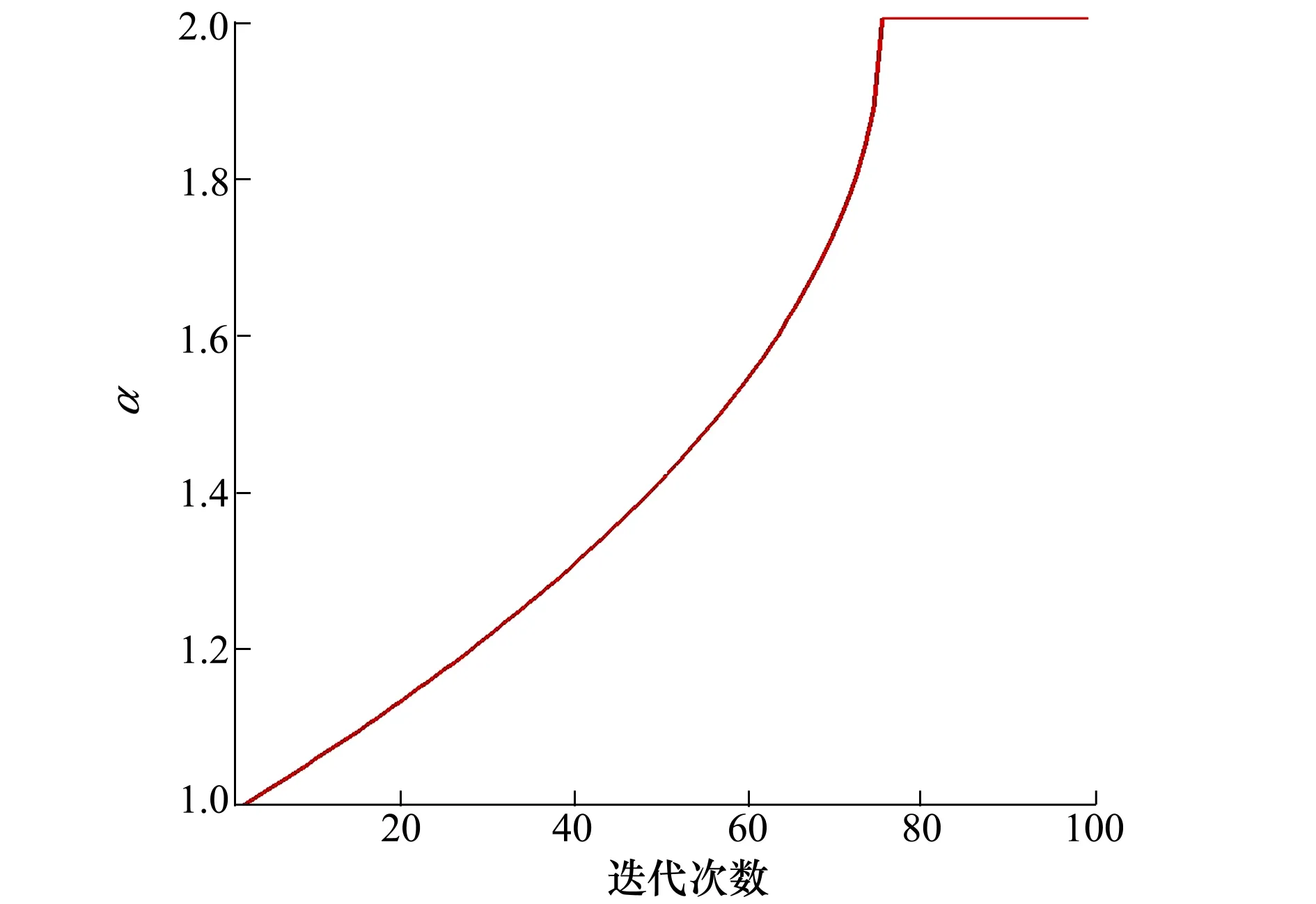
图4 α值的变化过程

2 算法验证

2.1 低维优化问题寻优能力检验

在低维优化问题的寻优能力检验中，3个优化算法的参数设定为：设计变量为30维，种群规模均取为100。基本PSO算法的惯性权重在[0.4,0.9]之间随代数线性递减。ASPSO算法的稳定性系数α的取值从1增加到2，变异策略为1.2节中所验证的设置3下凹型曲线。所有算法的加速常数c1=c2=1.5。分别用3种算法搜索运行30次，每次运行迭代1 000次，统计30次优化的平均目标函数值和搜索到的最小目标函数值。

表2显示了在低维优化问题上7个测试函数的检验结果。可以看出，不论是这7个测试结果的均值还是标准差，本文建立的ASPSO算法都是要优于其他2种算法。为了更突出地显示ASPSO优化算法的优化性能，在图5中，显示了3种优化算法在30维下的Rastrigin函数全局最优值收敛曲线。可以很明显地看出ASPSO算法甚至能在大量正弦拐点排列很深的局部最优点前提下直接搜索到最优解0，显示了其具有的优化性能。综合来说，在低维优化问题中，ASPSO优化算法优于DE算法以及PSO优化算法。

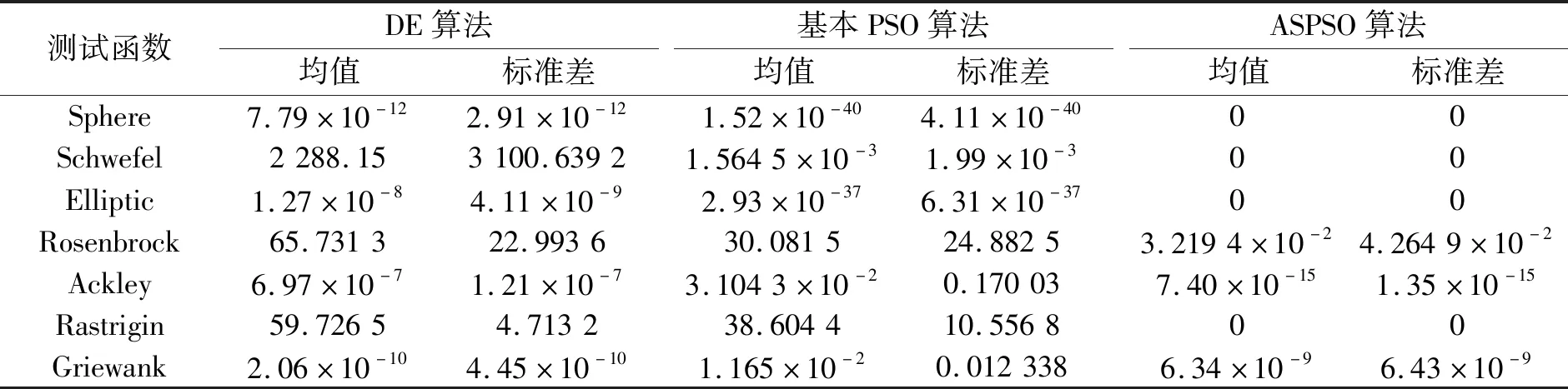
表2 低维优化问题计算效果对比

图5 3种算法在Rastrigin函数的低维优化全局收敛图

2.2 中、高维优化问题寻优能力检验

将设计变量分别扩展到60和100维，其他参数不变，测试3种算法在中、高维问题中的寻优能力。具体参数设置跟低维优化问题时相同，每种算法进行30次优化，每次进行1 000次迭代，最后统计得到这30次优化结果的平均目标函数值与最小函数值。

Rastrigin函数60维设计变量优化问题的全局收敛曲线见图6。7个函数的均值和标准差结果见表3。Rosenbrock函数的100维高维问题的收敛曲线见图7，7个函数的均值和标准差值统计结果见表4。可以看出随着维数的增加，3种算法的寻优精度都不同程度地降低，尤其是在高维优化问题中，寻优精度下降得很厉害。但是相比来看，在调用目标函数次数相同的情况下，ASPSO在平均值和标准差上都反映出了更高的精度，收敛效果更好，表明了其对于中、高维问题的较好适应能力。

图6 3种算法在Rastrigin函数的中维优化全局收敛图

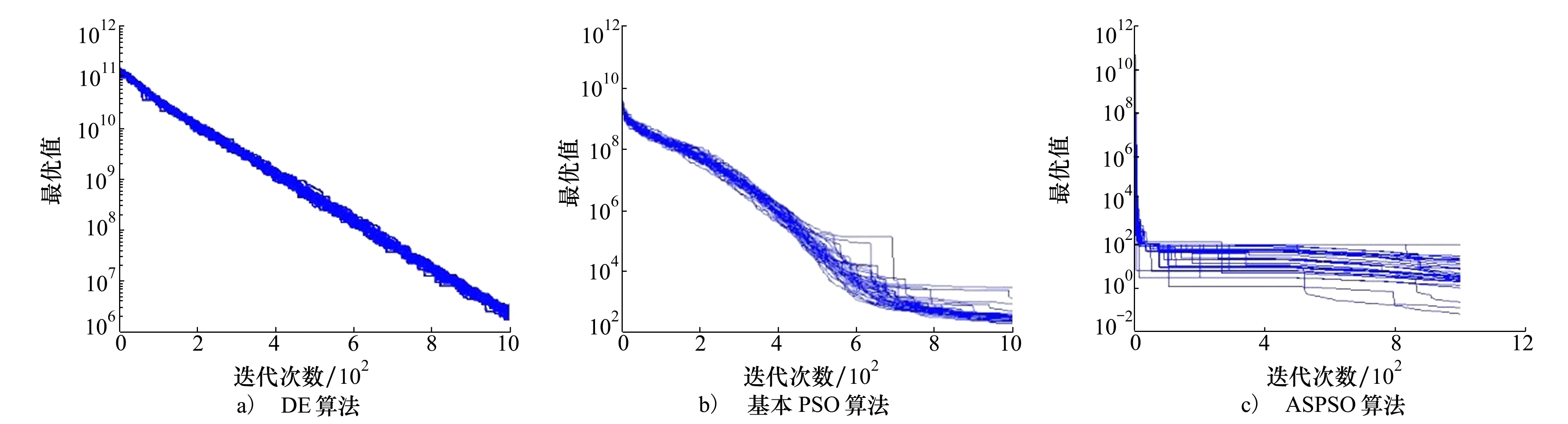
图7 3种算法在Rosenbrock函数的高维优化全局收敛图

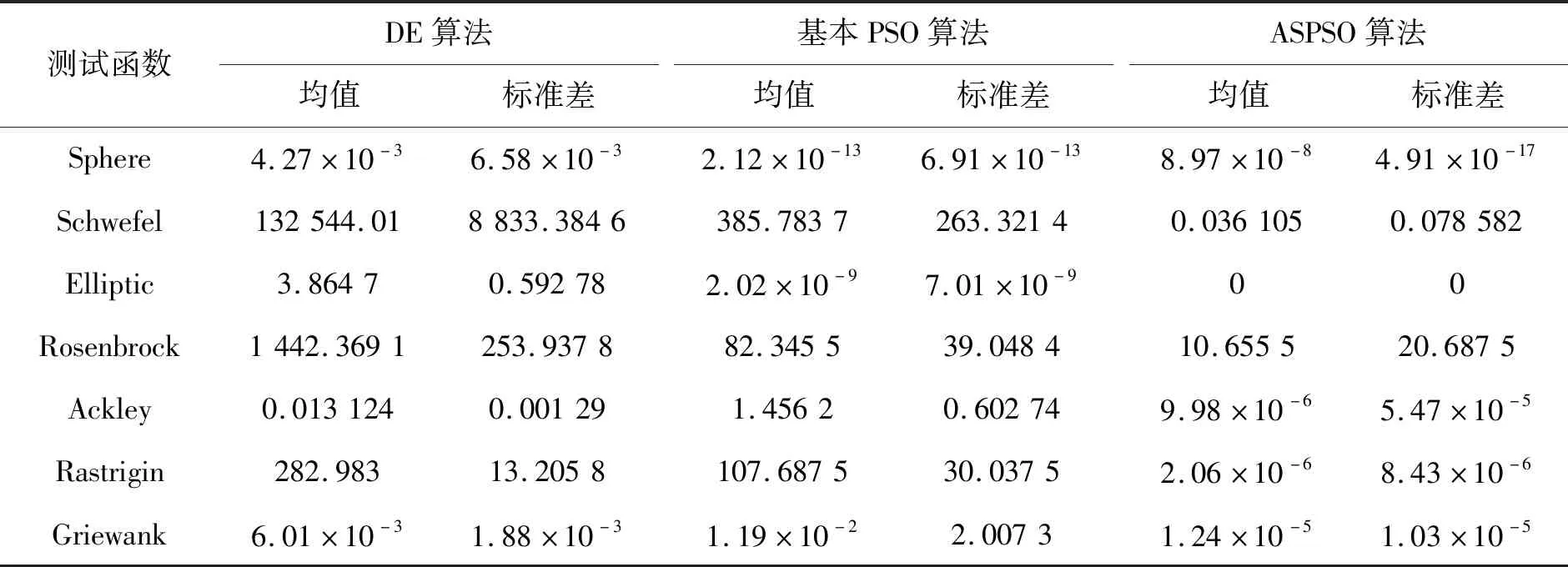
表3 中维优化问题计算结果对比

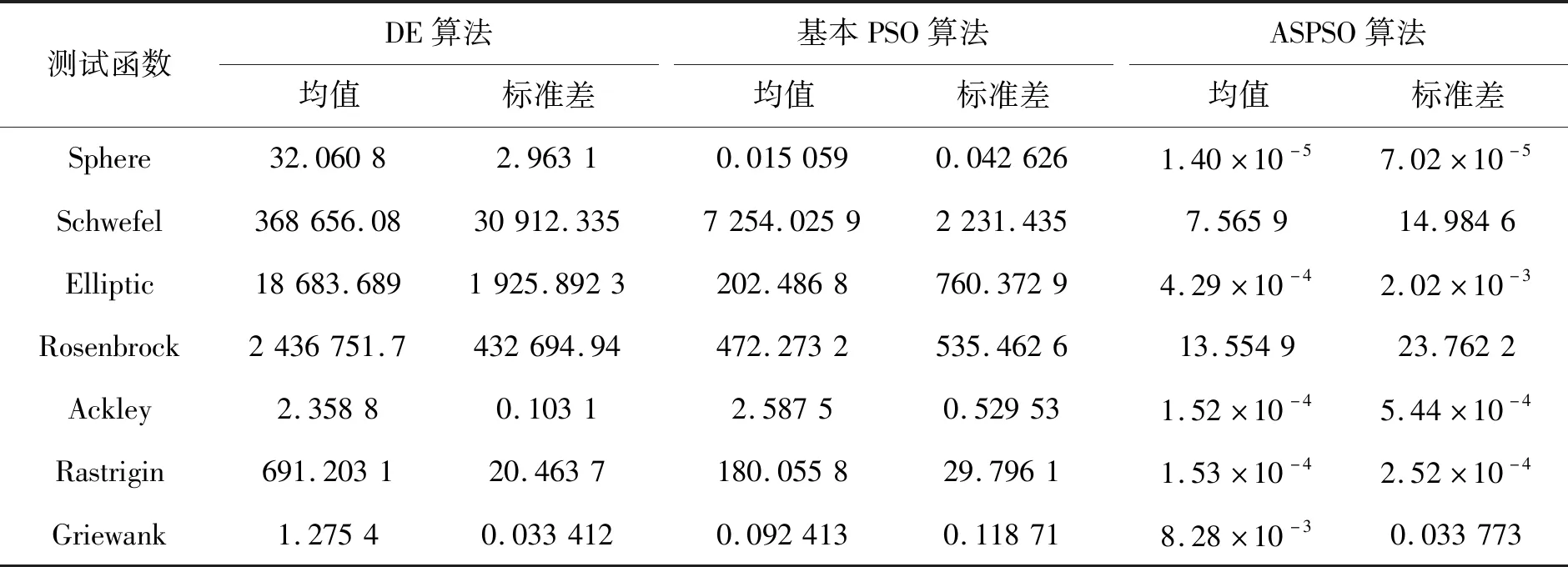
表4 高维优化问题计算效果对比

综上来看，无论是对低维还是中高维问题，相比基本PSO算法和DE算法，ASPSO算法都能够以更快的收敛速度、稳定性和鲁棒性获得单峰及多峰函数更高精度的最优解。同时还能够发现，以较为难以得到结果的Rosenbrock函数为例，在处理同一个函数不同维度的最优问题时，DE算法的性能相对较差，都无法寻优。而对比PSO与ASPSO算法，可以看出，中高维寻优中PSO算法有明显的性能下降，而ASPSO则体现了更为优秀的鲁棒性。所以相比其他2种算法，ASPSO是一种更加稳定且高效的全局优化算法。

2.3 多种PSO算法性能对比

为了能够更为全面地验证ASPSO优化算法的性能与优势，本节将选择多个先进PSO改进算法与ASPSO优化算法进行对比实验。本节选取的算法有：PSO-DAC(PSO based on dynamic acceleration coefficients)[10]、NDPSO(a normal distribution decay inertial weight PSO)[11]、EXPPSO(exponential decay weight PSO)[12]、SCVPSO(self-conclusion and self-adaptive variation PSD)[13]。PSO-DAC算法是基于动态加速因子的改进粒子群优化算法，通过引入动态的加速因子，改善粒子群算法的收敛速度及精度。NDPSO算法以正态分布曲线作为惯性权重的衰减策略曲线，引入控制因子对粒子的位置进行改善，使NDPSO算法能够在优化过程中很好地平衡全局搜索与局部搜索能力。EXPPSO算法在速度更新方程中引入约束因子，并对惯性系数采用指数衰减模式，使算法能够兼顾优秀的全局以及局部搜索能力。SCVPSO算法采用动态惯性权重、反向搜索以及引入新的参数SCR(self-conclusion rate)等方法综合性地提高粒子群的优化性能。本验证环节的算法参数设置为：设计变量为30维，种群规模均取为100。非特殊算法的惯性权重在[0.4,0.9]之间随代数线性递减。其余的采用其特有的惯性权重递减方式。所有算法的加速常数及ASPSO算法中的稳定性系数变化策略保持不变。为了全面验证算法的性能，验证算法选择单峰测试函数与多峰测试函数各3个。测试结果见表5。可以看出相比其他改进型PSO算法，ASPSO算法具有更为优秀的性能。

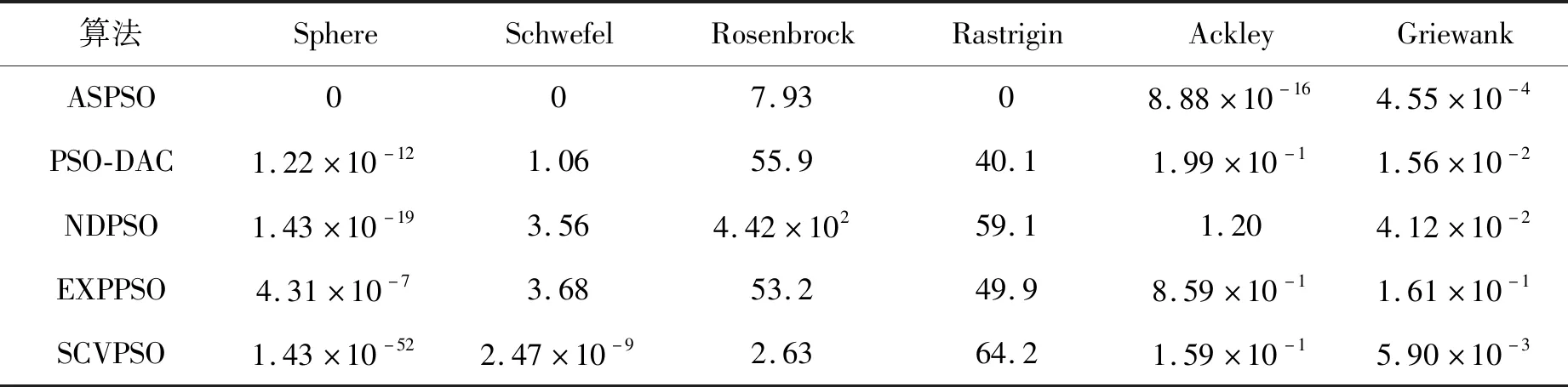
表5 多种改进PSO算法性能对比

3 优化算例分析

3.1 优化模型及参数化方法

为了更好地分析ASPSO算法在实际应用中的优化效果，选择对RAE2822翼型进行工程应用减阻优化。以其在Ma=0.73,α=2.79°,Re=6.5×106时的阻力最小为目标进行气动外形优化设计[14]，约束条件是优化后的翼型升力系数不小于原始翼型的升力系数值，并且翼型的最大厚度不减小，同时俯仰力矩不恶化。综上，可得到优化设计的数学模型：

式中：X为设计变量；Cd表示翼型的阻力系数;Cm表示翼型的力矩系数;Cl表示翼型的升力系数;cmax代表翼型的最大厚度,带上标*的符号表示原始翼型的气动数据。

针对RAE2822翼型，本节选用的是结合六阶Bernstein多项式型函数的CST方法作为翼型参数化方法。对翼型上下面各取6个(共12个)设计参数作为本次优化过程中的设计变量。

3.2 优化结果及分析

采用基本PSO算法与ASPSO算法2种方法对单点跨声速优化设计进行优化，比较2种方法的优化效果。2种优化算法的种群大小均为25，迭代步数为39，惯性权重w在[0.4,0.9]之间随代数线性递减。加速系数c1=c2=15。稳定性系数α变化范围为1.0至2.0。

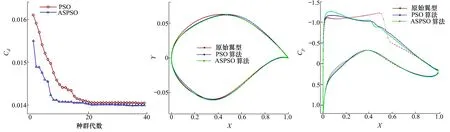
图8 减阻优化过程 图9 优化前后翼型剖面形状对比图10 优化前后压力分布对比

图8显示了2种优化算法的减阻优化过程，可以很明显看出ASPSO的优化程度与效率都优于基本PSO算法，ASPSO算法在第10次迭代时就能接近最终优化结果附近。在优化结果上来看，相比PSO算法，ASPSO算法能在保证优化程度上拥有更快的收敛速度。表6展示了2种优化算法的优化结果与原始翼型的气动参数对比，结果表明2种优化算法已满足基本的优化需求。图9与图10为优化前后的翼型的剖面形状以及压力分布。结合图9与图10可知，机翼的最大厚度后移，同时上表面翼面顶点的移动也使得优化后的翼型上翼面更加饱满，翼面激波有明显减缓，优化后的上翼面压力分布明显比原始翼型更加柔和。综合来看，针对RAE2822跨声速翼型的减阻优化，其结果显示波阻显著降低，升阻比有明显提高。相比于基本PSO优化算法，ASPSO算法有更优秀的适应性。在同样的种群数量和优化代数下，ASPSO算法具有更快的收敛速度以及更强的全局优化能力，优化结果也更理想。

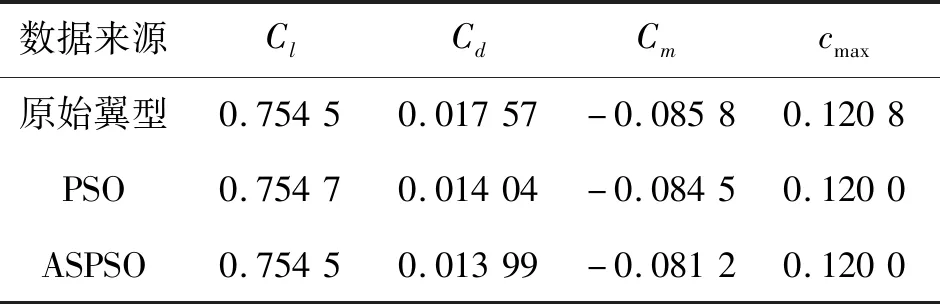
表6 优化前后的气动参数对比

4 结 论

本文针对粒子群算法容易陷入局部最优等缺点，通过Alpha stable分布产生的随机数对其进行变异操作，以实现粒子群优化算法优化性能的提高。通过测试函数验证了3种不同的α值变异策略对于粒子群优化算法的影响。选择了其中较优的变异策略参与进粒子群优化算法当中，使得算法在优化初始阶段能够更好地摆脱局部最优，在算法末期提高算法精度。

在多个测试函数验证环节中，选择了DE、PSO以及ASPSO 3种优化算法在低维以及中、高维优化问题中进行对比验证，结果表明ASPSO算法在单目标优化中优于DE及PSO算法。为了更进一步验证算法性能，横向对比多种改进策略下的PSO优化算法性能，选取了多种先进改进型PSO优化算法参与标准测试函数验证过程，结果表明ASPSO优化算法仍具有相当的优越性。综上所述，函数测试结果表明运用Alpha stable分布对PSO算法进行的变异过程的ASPSO优化算法具有优秀的性能。

最后，通过对RAE2822翼型进行工程应用减阻优化来验证ASPSO算法在工程应用上优于传统PSO算法。相比PSO算法，ASPSO算法的优化结果具有更好的力学特性，翼面波阻明显降低，ASPSO算法的优化结果拥有更好的气动性能。