大角度单摆振动周期近似公式的探究

◆北京市第三十五中学 王霞 王正阳 图/图虫创意

从秋千到老式钟表的钟摆，从日出日落到潮涨潮落，周期性变化的事物比比皆是。单摆就是这样一个具有周期性的物理模型，而最值得关注的、在生产生活中最有意义的是单摆的振动周期。

看似简单的振动，其周期的准确表达式却极其复杂。在教科书上，单摆小角度振动周期公式其应用在大角度振动时并不准确。能否找到一个合适的大角度振动周期的近似公式呢？

为解决这个问题，本文综合计算机模拟实验与回归分析，得到了一个估计效果较好的、大角度单摆振动周期的近似公式。

一、基本思路与研究目标

我们在一本物理教材上偶然看到单摆振动周期公式，并发现其备注为：只适用于小角度振动。这个公式说明，单摆在小角度振动下的周期只与摆长和当地的重力加速度有关，与初始摆角无关。为什么只适用于小角度振动？

带着疑问，我们对单摆进行了受力分析，并建立了微分方程，一探究竟。

图1 单摆的受力分析

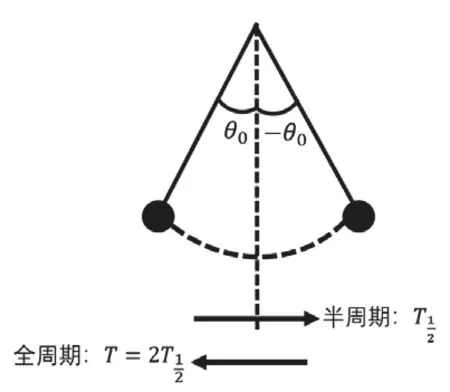
图2 单摆运动的周期

在求解方程中，计算到一个积分式便进行不下去了。我们想到了“只适用于小角度振动”，便没有放弃，又对被积函数在进行小角度下的泰勒展开，在略去一些项后，顺利得到了教科书上的单摆周期计算公式，感到茅塞顿开。紧接着便思考：能否把这个公式推广到更大的振动角度？这需要对那个难解的积分式进行研究。在查阅资料后得知，那个积分式是椭圆积分，用通项公式极难计算。

在信息课上，我们了解到回归分析的内容。通过回归分析，就能将许多具有一定关联的大量统计数据拟合出一个合适的函数，相当于用已知数据去“反向破解”产生数据的“黑盒子””的过程。

如果我们能获得大量椭圆积分的数据，便能“反向破解”出一个方便计算的拟合函数。我们还可以让计算机进行大量计算，得到椭圆积分的数据。

二、获取数据

（一）纯数学思路的尝试

要得到大量的椭圆积分数据，数学上的思路是直接利用椭圆积分的表达式，并通过逼近法求定积分。但椭圆积分是反常积分，即在边界值处被积函数会迅速增大，导致计算机处理困难，难以得到较准确的数据。纯数学思路在这里行不通。

（二）物理思路与计算机模拟实验程序设计

在理论推导过程中，我们已经知道椭圆积分Φ(θ0)和单摆运动半周期

周期是一个物理过程，可使用计算机模拟单摆振动这个物理过程得到，所以利用物理思路能解决这个问题。模拟实验程序流程如图3。

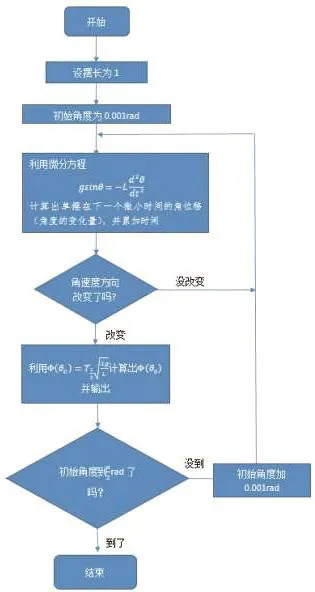
图3 模拟实验流程图

（三）程序运行

部分输出结果如表1（共1570个数据）。

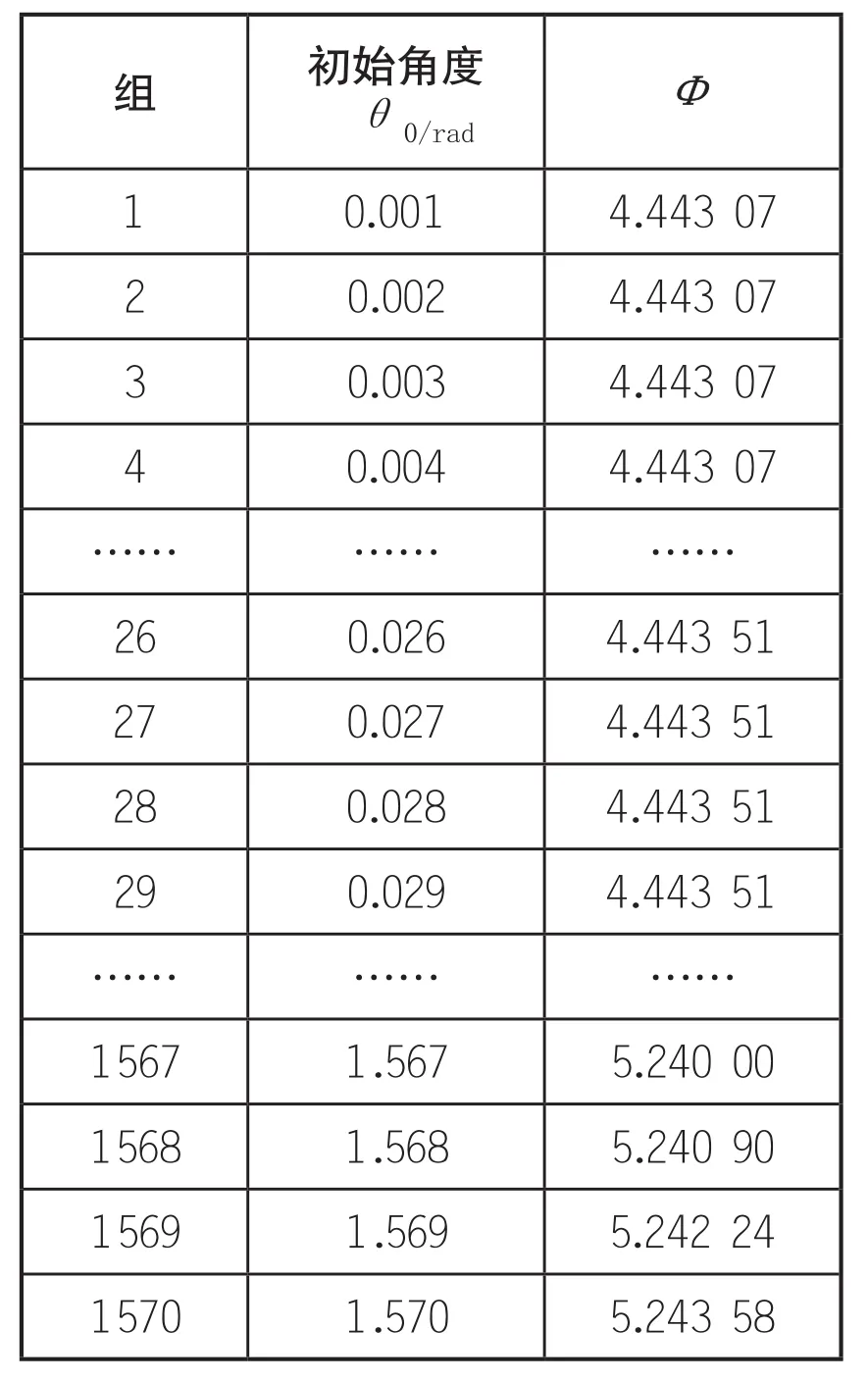
表1 部分输出数据

三、数据处理

（一）回归分析

运行程序得到初始角度θ0与Φ之间的数值关系，共1570个数据点。将其输入到EXCEL中，并绘制θ0与Φ之间的散点图。

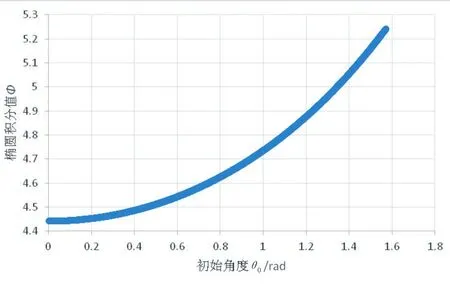
图4 数据散点图（截图）

观察Φ(θ0)图像的类型大致为类型的图像。因此，选用指数函数进行非线性回归。得到关系式0.103 9。

决定系数R2=0.930 6，代表拟合较好。但此时的和数值较难应用于实际计算，于是对估计值进行修正。

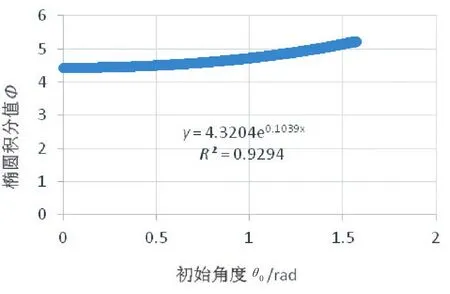
图5 指数非线性回归拟合（截图）

（二）误差分析

图 6 估计值与真值对比（截图）

（三）近似公式的确定

该式较简单，方便计算，并且能够较好地估计大角度单摆振动周期。

四、创新点

（一）实用性

本研究为大角度单摆振动周期的计算提供了一个较简单、方便计算并且估计效果好的近似公式。

（二）学科交叉

本研究从理论分析出发，基于物理过程创造性地提出了使用计算机模拟实验的方法获得实验数据，并使用非线性回归得出大角度单摆振动周期的近似公式。探究过程涉及数学分析、物理、统计学等多个学科，为学科交叉解决复杂问题提供了思路。