平均应力对AZ31B挤压镁合金棘轮行为的影响
2023-01-10韩重韬宋令慧段国升武保林
韩重韬,宋令慧,段国升,*,武保林
1. 沈阳航空航天大学 安全工程学院,沈阳 110136
2. 齐鲁工业大学(山东省科学院)山东省科学院新材料研究所 山东省轻质高强金属材料重点实验室,济南 250014
镁合金因其高比强/刚度、优良的阻尼和电磁屏蔽性能在航空航天和交通运输等领域的应用潜力巨大[1-2]。在服役过程中,镁合金构件不可避免地会受周期性载荷的影响,产生循环相关的疲劳问题[3-4]。近年来,循环应力导致塑性应变累积的棘轮行为受到密切关注。在非对称应力控制的循环过程中,棘轮应变是一个循环周期内最大应变和最小应变的平均值。由于棘轮应变,构件在承受疲劳损伤的基础上又叠加了棘轮应变损伤,严重影响构件使用安全可靠性[5-6],因此有必要对受应力作用的镁合金棘轮行为及影响棘轮应变形成的机制展开研究。
在形变孪生和织构的影响下,变形镁合金通常会表现出强烈的各向异性,其疲劳行为也与循环变形方式密切相关[7-11]。Lin等[12-14]研究了在单轴载荷下平均应力、应力幅对镁合金棘轮行为和低周疲劳行为的影响;Xiong等[15-16]调查了ZK60镁合金在不同平均应力和应力幅下的循环变形行为和棘轮现象;Wu等[17]研究了拉-拉循环应力控制下AZ31B镁合金循环变形组织与变形机制的关系及其对低周疲劳寿命的影响;Kang等[18-19]从加载路径和方式、温度等因素入手研究了镁合金棘轮行为的特点和变形机制,重点关注了不同加载路径下棘轮行为的变化规律。上述研究表明镁合金在位错主导的非对称循环应力下,往往表现出与面心立方金属和体心立方金属相似的棘轮行为。有别于位错滑移,孪生机制对镁合金循环变形的影响也不容忽视。研究发现镁合金循环变形的滞回曲线和Bauschinger行为受形变孪生的直接影响[20-21]。在早期研究中,笔者也发现位错主导的非对称应力循环下,临界剪切应力最小的{10-12}拉伸孪生在部分晶粒内启动[17]。从提供应变的角度看,{10-12}拉伸孪生启动的临界剪切应力(Critical Resolved Shear Stress, CRSS)较低,在提供一定变形量的同时还能促进基面滑移的启动,那么大量孪生的启动必然对棘轮应变产生影响。然而现有研究关于大量孪生对这种累积应变的影响并不明晰。由于变形镁合金的变形机制与载荷大小、方向密切相关,以平均应力作为应力控制循环变形的基本载荷参数,开展不同载荷状态下应力控制循环实验将有助于深入理解和认知形变孪生与变形镁合金棘轮行为之间的作用关系。
综上所述,通过开展一系列室温下的应力控制循环变形实验研究平均应力对AZ31B挤压镁合金循环变形行为及主导变形机制的影响,进而探讨不同载荷条件下棘轮应变的演变规律,以求阐明孪生机制对棘轮行为的影响机制。
1 实验材料及方法
1.1 实验材料
选择商业AZ31B挤压镁合金棒材为原材料,其主要成分为2.70wt% Al、0.96wt% Zn、0.21wt% Mn,其余为Mg。为消除内应力并获取均一组织,对原始棒材进行520 ℃/80 min退火热处理。图1(a)为退火后的组织形态,材料发生完全再结晶,晶粒基本呈等轴晶状,平均晶粒尺寸约40 μm。利用D-2000型X射线衍射仪对退火态棒材进行宏观织构测试,结果显示{0002}平行挤压方向(ED方向)为典型的纤维织构形态(如图1(b)所示,图中TD为垂直挤压方向)。

图1 退火态AZ31B挤压镁合金组织及其{0002}面极图
为开展应力循环实验,将退火棒材沿挤压方向加工成标距为20 mm、直径为10 mm的圆柱状样品,并对标距部分进行研磨抛光以满足循环测试要求。
1.2 实验方法
力学行为实验在MTS809多功能液压伺服试验机上进行。应力循环实验前分别开展应变率为10-3/s的单向拉伸和压缩实验以确定循环实验的载荷参数。应力循环实验以压-压形式进行,加载波形为三角波,加载频率为1 Hz,表1为循环实验中施加的平均应力及应力幅值,循环至2 000周次停止实验(按表1参数进行试验,发现棘轮应变在1 000周次循环后已处于稳定状态,满足研究不同加载状态下棘轮应变形成特征及孪生对其形成机制影响的目的,故选择循环至2 000周次停止实验)。
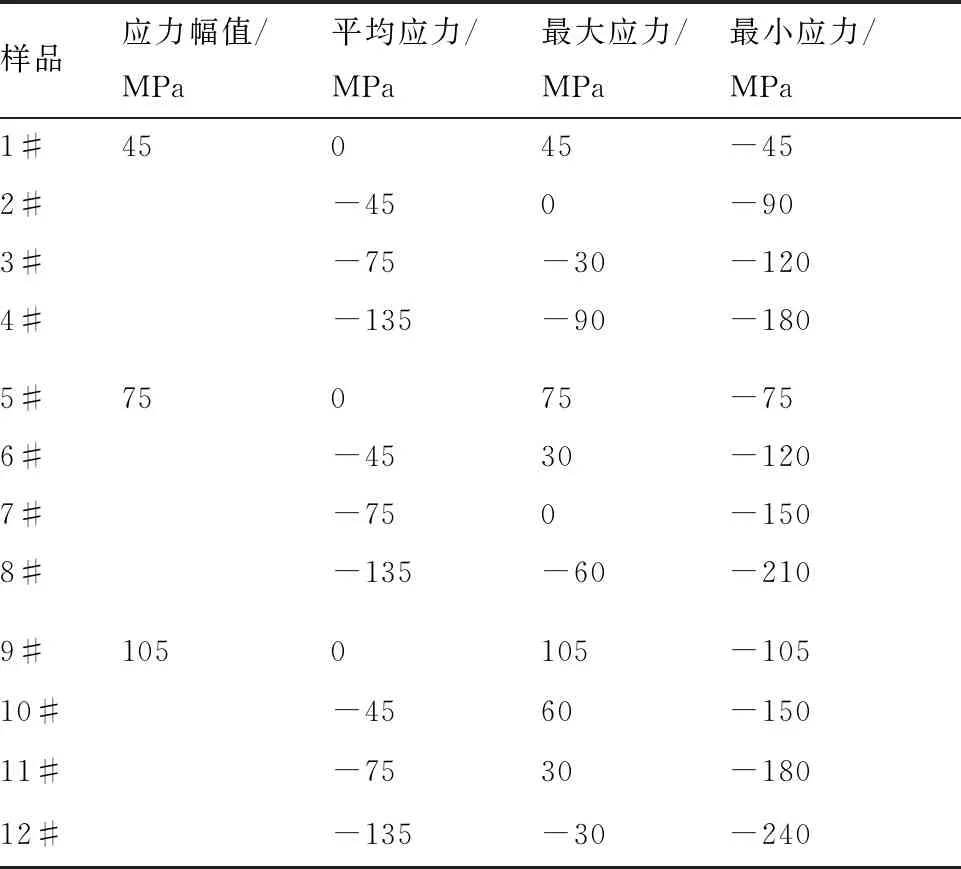
表1 应力控制实验循环加载工况
2 实验结果与分析
2.1 单向拉伸和压缩行为
图2为退火AZ31B挤压镁合金沿挤压方向拉伸和压缩的应力-应变曲线。单轴拉伸时应力-应变曲线呈以位错为主导的上凸形;单轴压缩时应力-应变曲线呈现出孪生和位错交替主导的S型特征。在图3所示应变与硬化率关系曲线中,样品硬化率在压缩时呈现出降低-增加-再降低的特征,表明AZ31B挤压镁合金在压缩过程中变形机制随应变发生改变[22-23]。主要原因是位错滑移与孪生之间的竞争,包括孪晶的产生、非基面滑移在孪晶中激活引起的硬化、非拉伸孪晶形成引起的软化及位错和孪晶界的相互作用[24-25]。根据样品合金纤维织构特征(如图1(b)所示),沿挤压方向施加压应力有利于CRSS较低的{10-12}拉伸孪生开动,硬化率下降[26];随着塑性变形推进,拉伸孪生不再增加,但可阻碍位错运动,孪生晶粒取向转变为“硬取向”,同时促进基面位错产生导致材料硬化率升高;进一步增加应变,位错累积效果减弱、材料内部出现缺陷影响,硬化率再次下降。表2为样品单轴拉伸和压缩的力学性能。
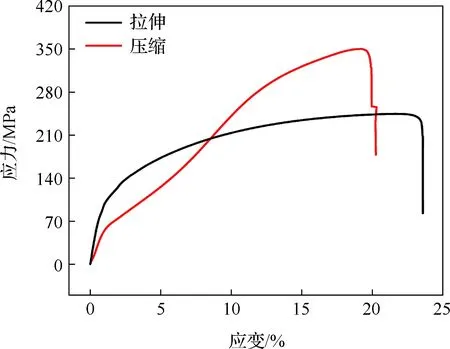
图2 AZ31B镁合金单轴拉伸和压缩的应力-应变曲线
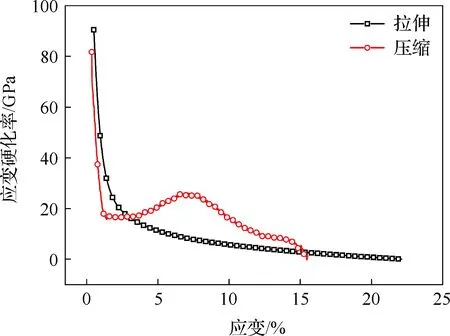
图3 AZ31B镁合金单轴拉伸和压缩过程的硬化率曲线

表2 AZ31B镁合金单轴拉伸和压缩的力学性能
2.2 压缩应力下的循环变形行为
实验中设定压缩平均应力分别为0、-45、-75、-135 MPa,研究应力幅值分别为45、75、105 MPa时上述平均应力下的循环变形行为。选取循环次数为第1~5、50、100、1 000、2 000周次下的滞回曲线(如图4和图5所示)做对比研究。
图4为应力幅值45 MPa时不同平均应力作用下的循环应力-应变曲线。当平均应力为0 (如图4(a)所示)时,试样所受最大/最小应力为±45 MPa,均低于单向拉伸/压缩的屈服应力,材料处于弹性变形阶段;不同循环周次的滞回曲线位置显示在拉伸端未发生较明显的应变累积,未发生棘轮行为。当平均应力为-45 MPa(如图4(b)所示)时,滞回曲线位置随循环次数增加发生变动,塑性应变累积出现。图4(c)和图4(d)分别为平均应力-75 MPa和-135 MPa时的应力-应变曲线,可见在循环初期前100周次的滞回曲线位置发生明显变化,沿应变负方向推移,这表明此时已存在明显的应变累积;随循环进行,1 000~2 000周次的滞回曲线位置变化不明显,循环已进入稳定期。
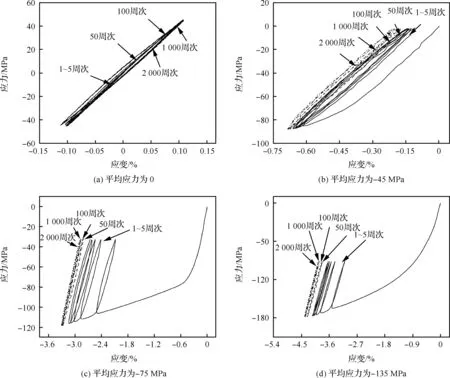
图4 应力幅值为45 MPa时不同平均应力下的循环应力-应变滞回曲线
当平均应力为-75 MPa(如图4(c)所示)时,根据图2和图3所示应力-应变关系曲线可知,压缩过程中应有大量拉伸孪晶出现。在循环初期滞回曲线围成的面积较大,这是循环过程中孪生-去孪生变形机制的作用。随循环不断进行,滞回曲线面积减小,这意味着主要循环变形机制由孪生-去孪生逐步转变为位错滑移。在平均应力为-135 MPa(如图4(d)所示)时,材料经初次压缩后发生了较大的塑性变形,位错滑移起主导作用,同时材料内部也伴有大量的拉伸孪晶或压缩孪晶出现。然而在循环过程中最大应力始终处于负应力水平,去孪生行为在循环卸载时受抑制,基面滑移主导塑性变形,材料表现出较高的应变硬化。
图5为应力幅值75 MPa时不同平均应力下的循环应力-应变关系曲线。当平均应力为0(如图5(a)所示)时,50~2 000周次的滞回曲线重合,形状和位置变化不大,表明此条件下循环快速进入稳定期。随平均应力增加,图5(b)~图5(d)的滞回曲线位置呈现出与图4中一致的现象,即向压缩方向(负应变方向)移动。与平均应力为0时相比,平均应力为-45 MPa(如图5(b)所示)时滞回曲线围成区域变大,呈对称透镜状,滞回曲线在压缩方向上应变累积愈发明显,滞回曲线之间位置更加拉开,材料表现出应变软化现象。然而随平均压应力增加,滞回曲线围成区域明显减少(如图5(c)和图5(d)所示),这一点在图6所示的第5、100、1 000周次循环下滞回曲线对比中可明显看出。在相同平均应力(如图6所示)下,滞回曲线所围面积随循环次数的增加逐渐减少;随平均压应力增加,在相同循环周次时滞回曲线所围面积先增大后减小。
由于应力幅值为75 MPa、平均应力为0(如图5(a)所示)时压缩应力超过了孪生启动所需的临界剪切应力,材料中小部分取向有利的晶粒率先发生孪生,而大部分晶粒则以位错滑移的方式协调变形;卸载过程中部分孪生晶粒发生去孪生,而未发生孪生的晶粒则以位错滑移的方式参与卸载和反向拉伸过程。当平均应力为-45 MPa和-75 MPa(如图5(b)和图5(c)所示)时,拉伸端和压缩端最大应力分别为30 MPa和-120 MPa、0和-150 MPa。为明确形变组织与循环行为的对应关系,选取应力幅为75 MPa、平均应力为-75 MPa时不同循环阶段组织及相应{0001}极图(如图7所示)进行说明。在初次循环压缩至最大应力-150 MPa(如图7(b)所示)时大部分晶粒发生孪生,相比初始组织{0001}极图(如图7(a)所示)发生了明显偏转,在反向卸载过程中部分晶粒将发生去孪生过程,在循环的初始阶段孪生-去孪生机制在循环过程中占重要地位。当循环至1 000周次后(如图7(c)所示),组织中存在大量未发生去孪生的残余孪晶,与图7(b)所示{0001}极图相比,更多晶粒由于孪生取向发生改变。此时位错与位错之间及残余孪晶与位错之间发生交互作用,相应的滞回曲线转化成扁平直线状;当循环至2 000周次(如图7(d)所示)时,残余孪晶数量进一步增加并碎化,位错缠结更加严重,材料硬化进一步加剧,滞回曲线形态进一步变窄。由此可证明循环过程中变形机制与应力-应变曲线的对应关系。
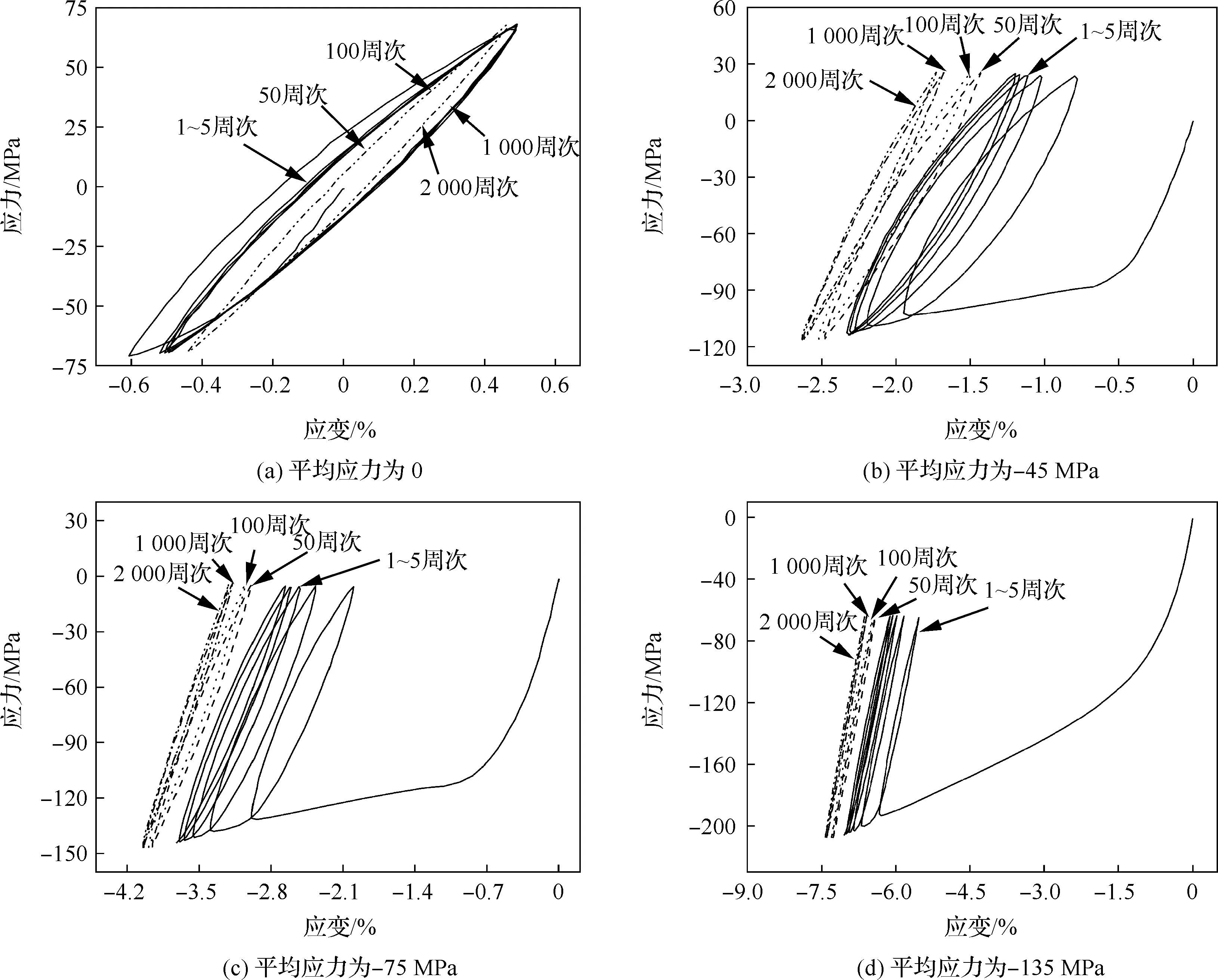
图5 应力幅值为75 MPa时不同平均应力下的循环应力-应变滞回曲线
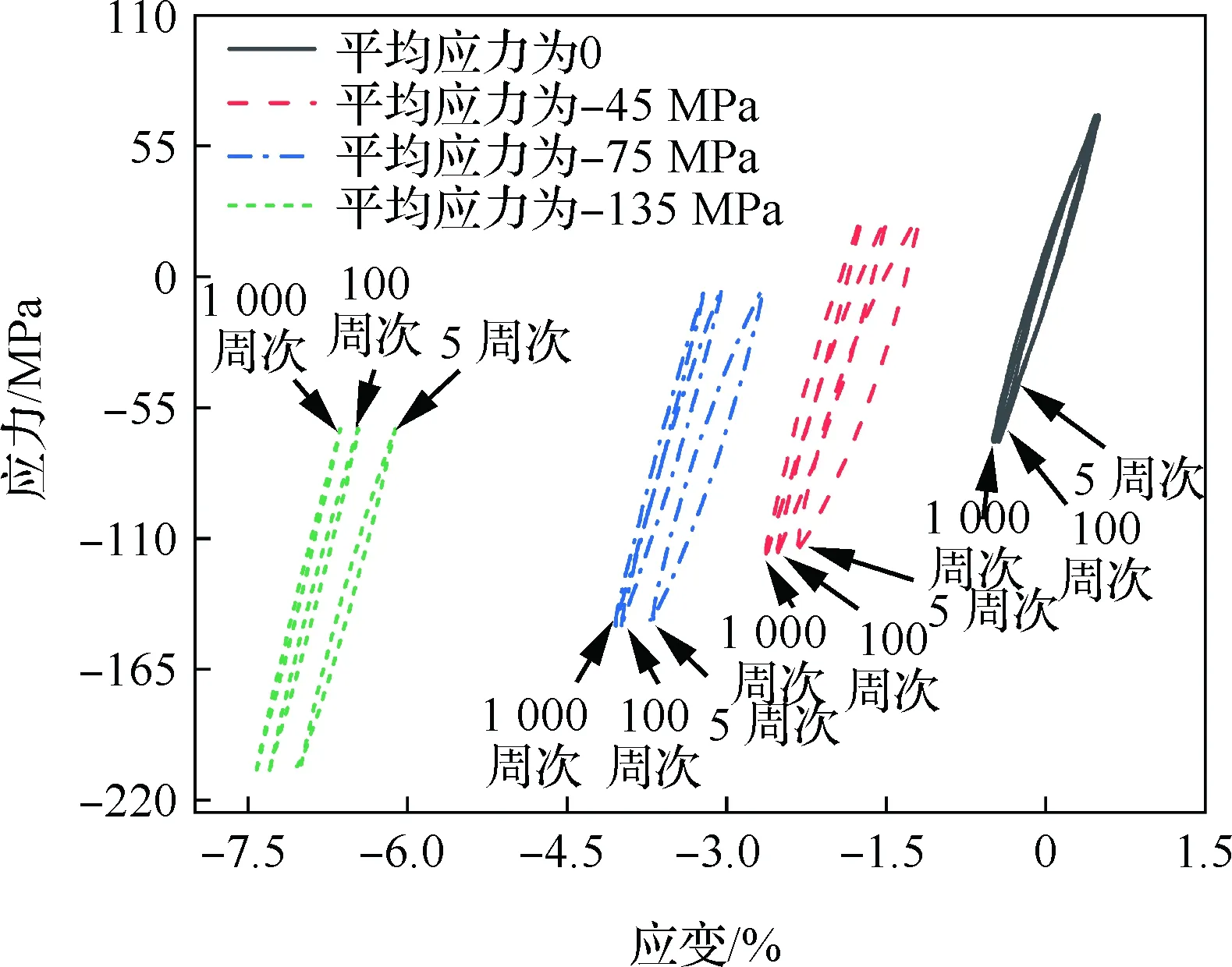
图6 应力幅值为75 MPa时第5、100、1 000周次循环的滞回曲线

图7 应力幅值为75 MPa、平均应力为-75 MPa时不同循环阶段的微观组织
当平均应力为-135 MPa(如图5(d)所示)时,最大应力和最小应力分别为-60 MPa和-200 MPa。在第1周次的压缩阶段之后,取向有利的晶粒基本都完成了孪生过程,晶体取向发生彻底转变,基面近似垂直于载荷方向;卸载时大多数晶粒的c轴仍受压应力影响,并不能完成相应的去孪生过程,在后续循环过程中以位错滑移的形式参与变形,这与图4(d)所示情形一致。
图8为应力幅值105 MPa时不同平均应力下的应力-应变曲线。当平均应力为0、-45、-75 MPa时拉伸端和压缩端应力分别为105 MPa和-105 MPa(如图8(a)所示)、70 MPa和-150 MPa(如图8(b)所示)、40 MPa和-180 MPa(如图8(c)所示),在上述应力范围下循环过程中均有孪生-去孪生机制参与,滞回曲线形态均呈现透镜状。平均应力为-135 MPa(如图8(d)所示)时应力极值分别为-20 MPa和-240 MPa,在压缩过程中大多数晶粒发生孪生,但-135 MPa的平均应力使材料始终处于压缩状态,限制了去孪生活动的进行,大量拉伸孪晶残留,促进了后续循环中位错机制的启动。
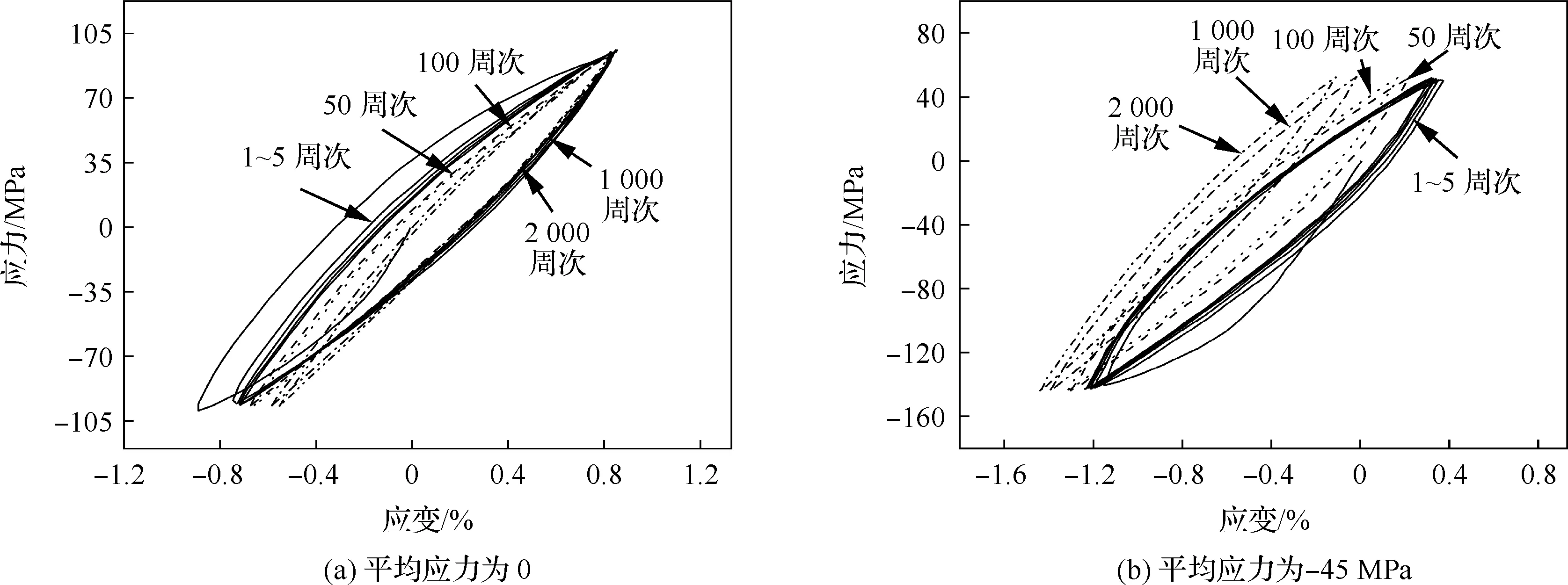
图8 应力幅值为105 MPa时不同平均应力下的循环应力-应变滞回曲线
3 平均应力对棘轮应变及演化过程的影响
由2.2节可知棘轮应变在应力控制循环初期变化显著。如引言部分所述,棘轮应变εm为一个循环周期中最大应变εmax和最小应变εmin的平均值,即εm=(εmax+εmin)/2,反映循环过程中材料沿平均应力方向的定向“平移”特征。区别于棘轮应变,塑性应变幅常用于反映材料损伤程度和循环硬化/软化特征,它是一个循环周期中最大应变εmax和最小应变εmin之差的平均值,即εp=(εmax-εmin)/2。为更加明确地揭示棘轮行为在循环变形中的行为特征,选择塑性应变幅进行对比分析。
以应力幅值为105 MPa的情况为例,图9为应力幅值105 MPa时不同平均应力下塑性应变幅与循环次数的关系曲线。可见随循环次数增加,塑性应变幅降低;循环初期应变幅快速下降,表现出显著的循环硬化特征;稳态阶段塑性应变幅缓慢降低并趋于稳定。平均应力对塑性应变幅影响显著,随平均应力增大,塑性应变幅逐渐减小;这表明循环过程的平均应力越大,材料的循环硬化越显著,硬化率增加量随循环周次增加逐渐减小。
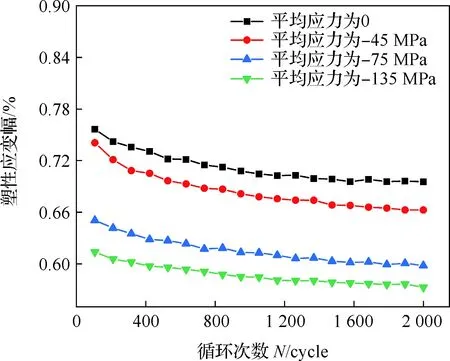
图9 不同平均应力下塑性应变幅随循环次数的变化
图10~图12分别为应力幅值45、75、105 MPa时棘轮应变随循环次数的演化曲线。当应力幅值为45 MPa(如图10所示)时平均应力为0的棘轮应变几乎不变;随平均应力减小,棘轮应变也逐渐减小。棘轮应变随循环次数增加逐渐增大(沿压缩方向增加),一定的循环次数后趋近于一个相对稳定的状态。
平均应力为-45 MPa时基面滑移主导循环变形过程,此时产生的棘轮应变较小,棘轮应变约为-0.44%。平均应力为-75 MPa时孪生-去孪生机制主导了前3个周期的变形;在第3个循环结束后棘轮应变为-2.78%;随循环进行材料发生硬化,棘轮应变增长缓慢。由此可见此时棘轮应变主要来自孪生主导的变形过程,孪生-去孪生对棘轮应变的“贡献”大于位错滑移机制。在平均应力为-135 MPa时,经第1周次压缩后材料内部生成了大量拉伸孪晶,织构发生改变;而卸载过程的去孪生行为较弱,此时大部分晶粒处于基面滑移的有利取向,棘轮应变主要由位错滑移提供;随循环进行位错滑移逐渐由多滑移模式转向交滑移模式,在循环后期形成了复杂的高密度位错组态[23]。对比棘轮应变大小,发现相比平均应力为0、-45、-75 MPa下棘轮应变大幅增加,说明孪生-去孪生机制相比位错机制更易产生棘轮应变。
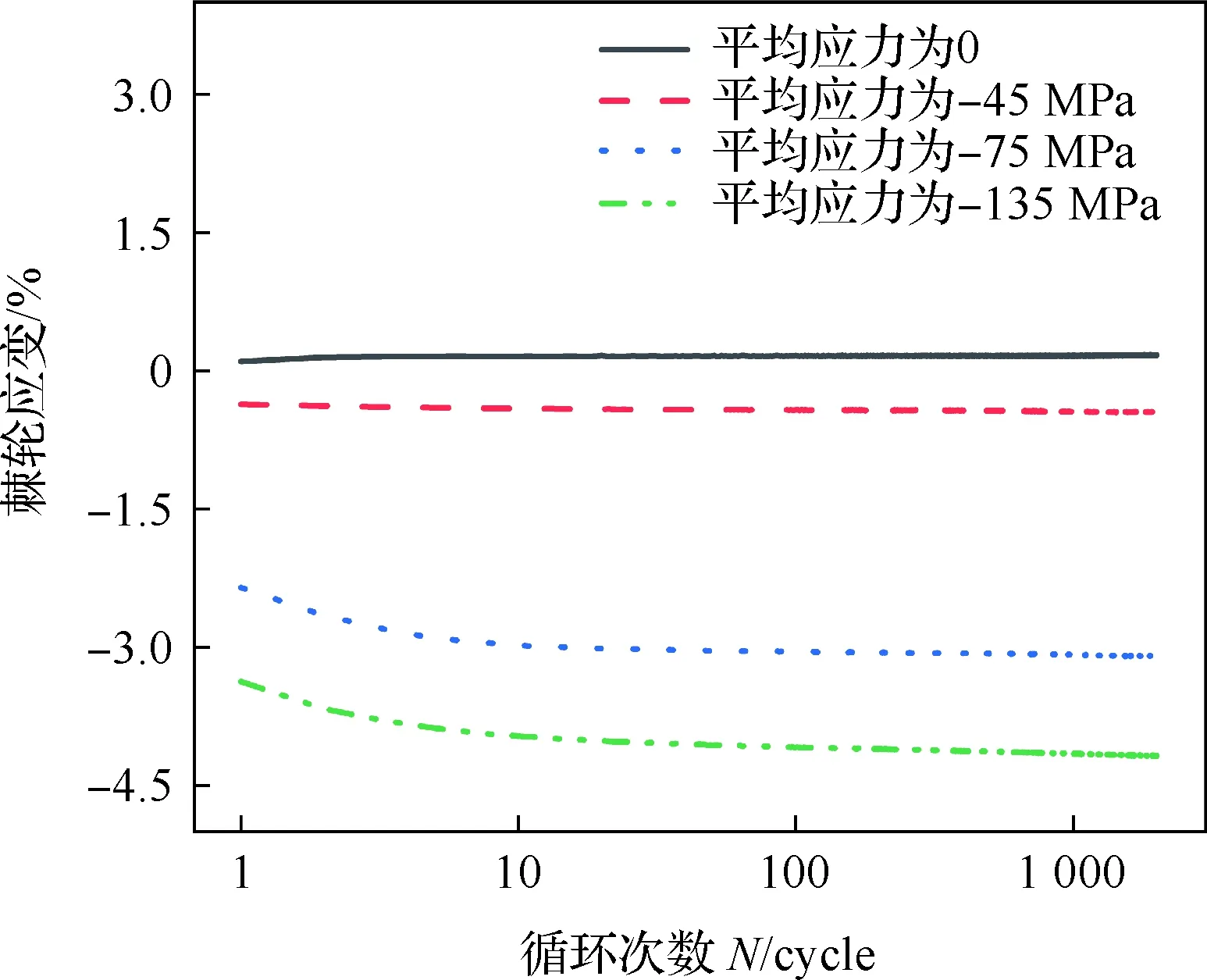
图10 应力幅值为45 MPa时的棘轮应变演化曲线
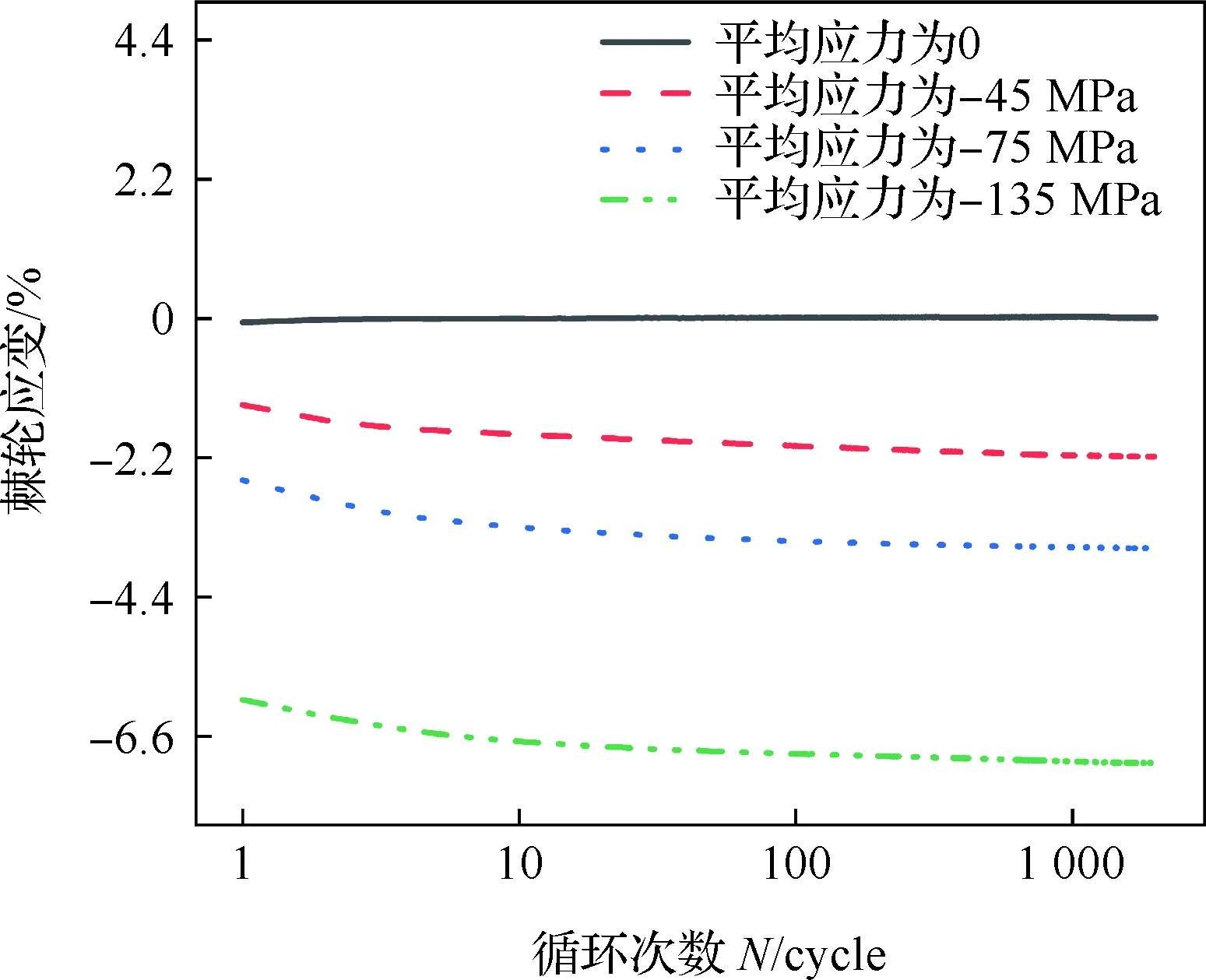
图11 应力幅值为75 MPa时的棘轮应变演化曲线
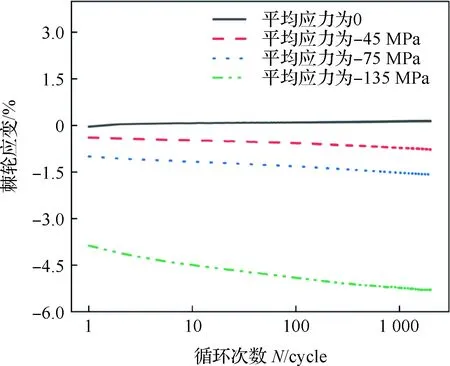
图12 应力幅值为105 MPa时的棘轮应变演化曲线
图11为应力幅值75 MPa时的棘轮应变演化曲线,前20周次循环的棘轮应变率曲线如图13所示。可见平均应力为0时几乎不存在应变累积的棘轮效应;其他平均应力条件下棘轮应变在100周次循环周次后达到一个稳定值,分别为-2.18%、-3.63%和-7.02%。平均应力为-45 MPa时孪生-去孪生机制在前100个循环周期内所占比重大,此时棘轮应变与孪生机制紧密相关。相比于图10中平均应力为-45 MPa时的状况,棘轮应变由-0.44%增大到-2.18%,可见孪生变形机制对棘轮应变有明显的促进作用。平均应力为-75 MPa时,孪生-去孪生主导了前50周次的循环变形,棘轮应变达-3.47%;随着循环进行变形机制转变为位错滑移,棘轮应变略有增加。在平均应力为-135 MPa时,循环初期形成的大量孪晶改变了材料织构类型,位错滑移主导塑性变形,棘轮应变在前十几个周期快速增加后缓慢增长。
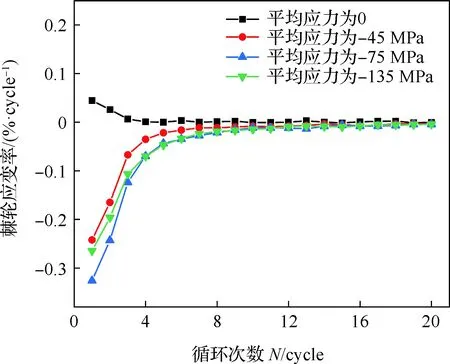
图13 应力幅值为75 MPa时不同平均应力下前20周次循环的棘轮应变率曲线
对比应力幅为75 MPa时的应变率曲线(如图11和图13所示)发现,棘轮应变随平均应力绝对值的增加而增加,但棘轮应变率并未随平均应力发生单调变化。在平均应力为-75 MPa时孪生-去孪生变形机制促进了棘轮应变的增加。在-135 MPa时第1周期初始压缩过程耗尽了孪生的有利取向,后续循环过程中棘轮应变率明显小于平均应力为-75 MPa时的棘轮应变率。
图12为应力幅值105 MPa时棘轮应变与循环次数的关系曲线,前20周次循环的棘轮应变率曲线如图14所示。当平均应力为-45、-75、-135 MPa时循环在600周次后进入稳定,此时的累积应变分别为-0.77%、-1.57%和-5.38%。应力幅值为105 MPa时作用在材料上的应力足够使其发生压缩屈服,在初始压缩阶段生成大量的拉伸孪晶,同时大量位错激活;压缩平均应力越大,孪晶越能充分生长,以致改变基体晶粒取向;由于始终处于压缩状态,在卸载过程中这些取向发生改变的晶粒去孪生行为不能像孪生行为那样充分进行,残余了大量拉伸孪晶。由此可见孪生行为的充分发展和不完全的去孪生行为影响了循环过程中棘轮应变的增加。
对比图12和图14可知棘轮应变随循环次数的增加而增加,棘轮应变率随循环次数的增加逐渐减小。而棘轮应变形成的循环过程中孪生-去孪生为主要变形机制。孪生-去孪生机制使循环变形前期的棘轮应变率明显高于循环后期位错变形机制主导的棘轮应变率,同时孪生-去孪生机制引起的应变硬化率低于位错机制引起的应变硬化率。
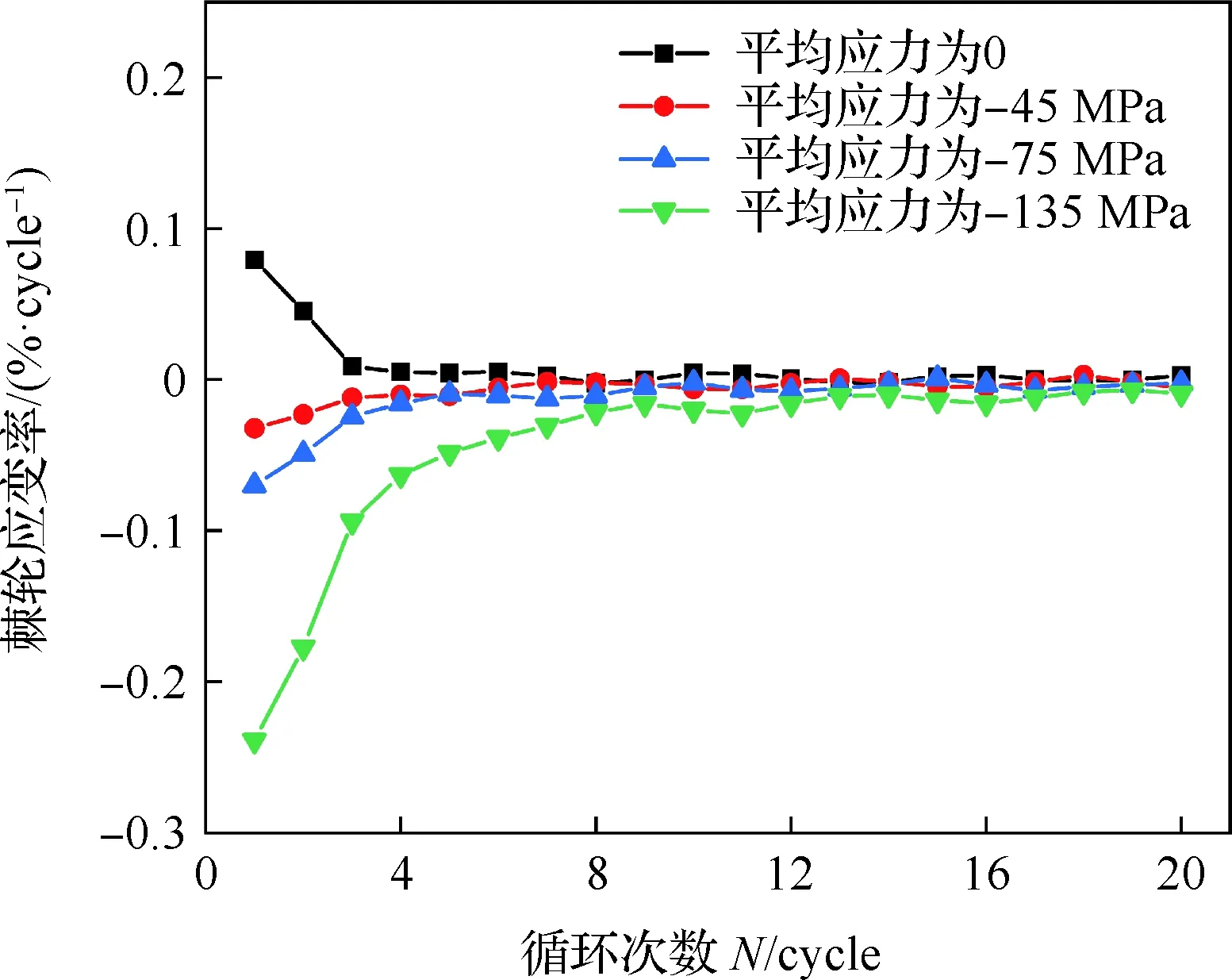
图14 应力幅值为105 MPa时不同平均应力下前20周次循环的棘轮应变率曲线
4 结 论
对AZ31B挤压镁合金开展了应力控制循环变形实验,得到的主要结论如下:
1) 当平均应力为0时在拉伸方向上产生微小的棘轮应变,这来源于变形镁合金的拉/压不对称性。
2) 压缩应力超过75 MPa时孪生机制启动,随循环进行主导塑性变形的机制由孪生-去孪生机制逐渐转变为位错滑移机制。相比于位错滑移,循环变形中孪生-去孪生机制促进了棘轮应变的增加。
3) 在压应力控制循环变形过程中,棘轮应变均在循环初期(约前100~200周次)急剧增加,随循环次数增大而增大,棘轮应变率减小,且在一定循环次数后棘轮应变趋于稳定。
4) 在孪生-去孪生机制参与的循环过程中,孪生-去孪生机制在循环过程中对棘轮应变的“贡献”远大于位错机制的作用。
