基于马尔科夫链的城市轨道交通客流量预测研究

吴 珉

(1.合肥工业大学 管理学院，合肥 230000；2.安徽工业经济职业技术学院 电气工程学院，合肥 230051)

城市轨道交通客流量预测是进行城市轨道交通规划以及运营指导的关键，通过对客流量的准确预测来有效地安排发车的间隔，为旅客提供高质量的服务。温惠英等[1]基于深度学习的理论框架，建立了地铁短时客流量预测的双向长短期记忆网络模型，同时以广州体育西站地铁站数据为实例进行验证，指出所建立的模型平均预测精度超过90%。赵鹏等[2]建立了城市轨道交通进站量预测的自回归积分滑动平均模型(Autoregressive Integral Moving Average Model，ARIMA)，指出ARIMA模型对城市轨道交通进站量预测的平均误差仅仅为4%，具有比较高的进站量预测精度。陆文星等[3]采用改进粒子群算法(Particle Swarm Optimization，PSO)优化反向传播(Back Propagation，BP)网络的初始权值与偏置，构建了黄山风景区日客流量预测的PSOBP模型，并指出所构建的预测模型具有比较好的鲁棒性，预测精度大大提升。梁强升[4]采用灰色预测理论构建了大型活动期间地铁车站客流量预测方法，将其应用于2018年秋季广交会地铁车站客流数据预测中，预测结果表明所构建的预测模型对地铁车站客流量具有比较高的预测精度。城市轨道交通客流量的预测直接影响轨道交通的运行质量和运营成本，传统的预测方法是非实时的。马尔科夫链通过转移矩阵和转移图来定义，在随机量预测中具有广泛的应用。基于此，将GM(1，1)模型和马尔科夫链联合构建城市轨道交通客流量预测模型，并应用于郑州市2号线的14个站点客流量预测中。

1 轨道交通客流量预测建模

1.1 GM(1，1)模型

GM(1，1)模型是灰色系统理论中被广泛应用的一种灰色动态预测模型，其由单一变量的一阶微分方程所构成。GM(1，1)模型预测的原理是对数据序列通过累加的方式来生成具有明显趋势的新数据序列，对具有明显趋势的新数据序列建立预测模型，然后再通过累减逆向运算恢复原数据序列，从而进行数据预测[5]。采用GM(1，1)对城市轨道交通客流量预测的流程如图1所示。

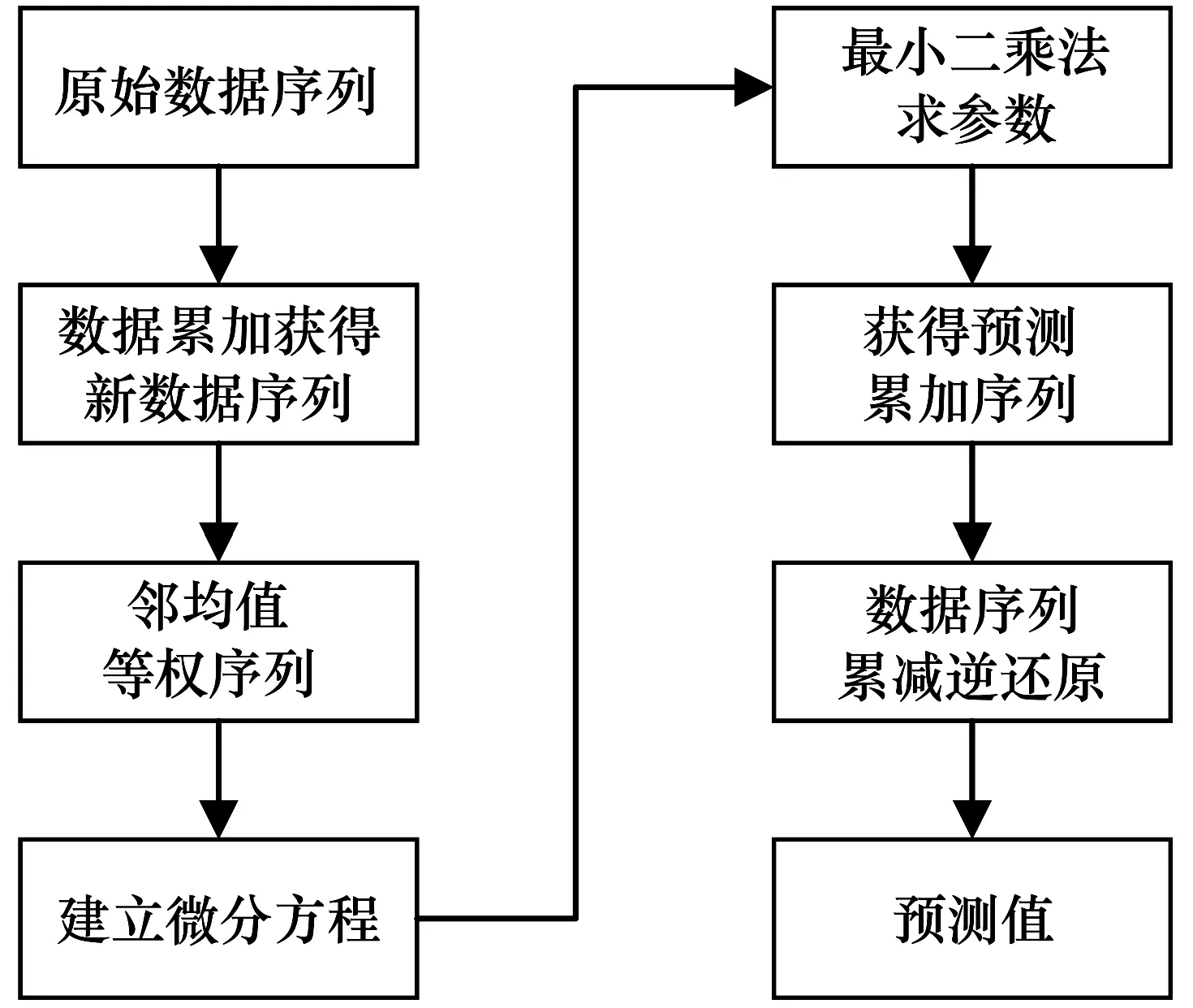
图1 GM(1，1)城市轨道交通客流量预测流程

以城市轨道交通中的地铁交通为例，设前n-1个站点客流量(上下车人数的总和)为X(0):

考虑到站点客流量的随机性和波动性比较大，通过累加的方式来弱化序列的随机性与波动性，获得累加后的新数据序列X(1):

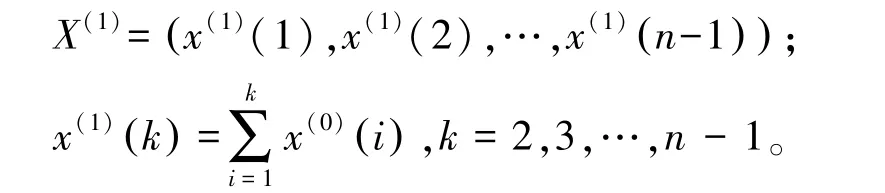
由X(1)构造邻均值等权序列Z(1):

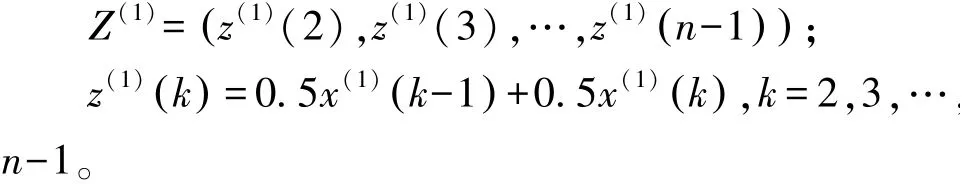
根据灰色理论构建关于t的微分方程GM(1，1)，即

式中:a为发展系数；u为灰色作用量。

令A=[a，u]T，由最小二乘法估计可以得到:

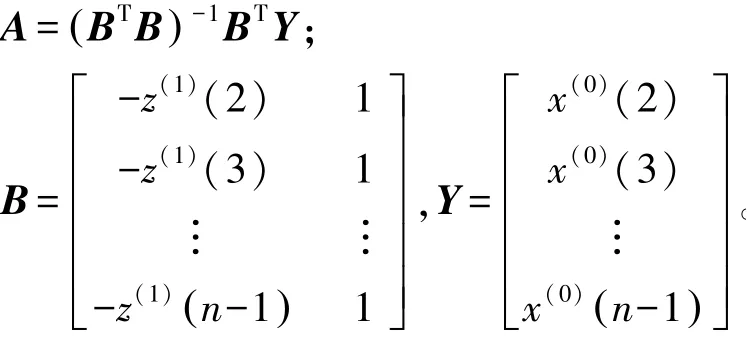
将A代入式(1)求解得到:

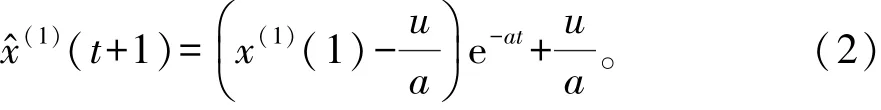
对式(2)进行累减逆还原即可以得到站点客流量预测值，即

1.2 马尔科夫链

为了确保采用GM(1，1)模型对地铁站客流量预测的准确性，必须对建立了的GM(1，1)模型进行精度检验。采用GM(1，1)模型预测前n-1个站点的客流量，即

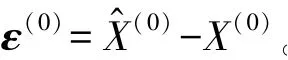
对残差向量ε(0)进行傅里叶级数展开，即

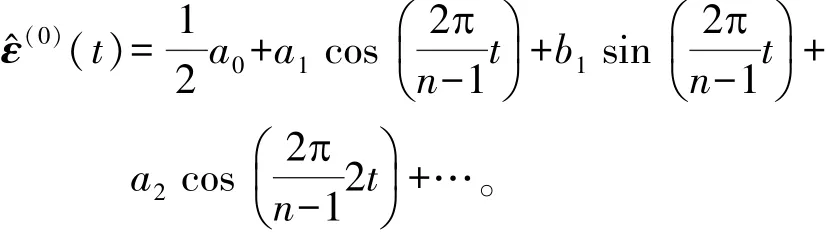
为了消除噪声以及其他因素的干扰，取残差向量ε(0)傅里叶级数展开式的部分项，即

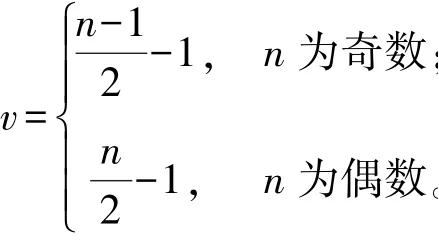
令c=[a0，a1，b1，…，av，bv]，由最小二乘法可以得到:

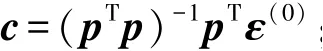
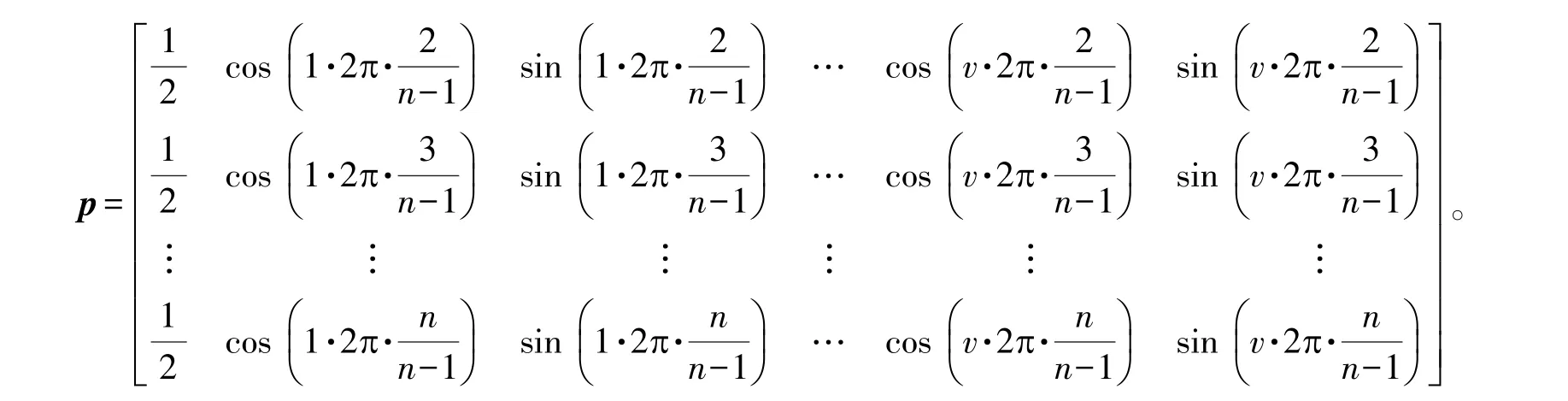
由残差向量ε(0)傅里叶级数展开式的部分项得到马尔科夫链的状态总数q，同时计算状态转移矩阵p[6]。用nij表示状态转移矩阵p第i行第j列的元素，定义

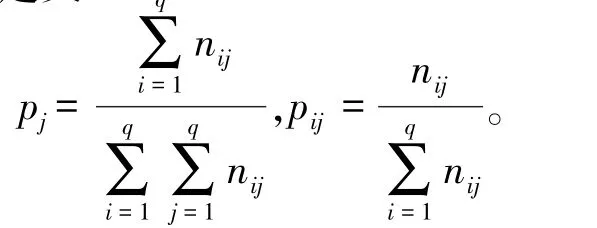
构造检验统计量，即

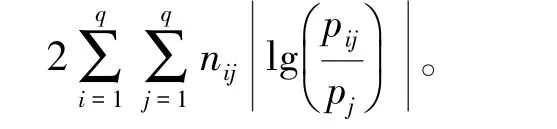
该检验统计量服从自由度为(q-1)2的χ2分布。定义置信水平为α，如果满足

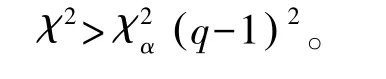
那么满足马氏性，否则增加残差向量ε(0)傅里叶级数展开式的项数，直到满足马氏性为止。

1.3 轨道交通客流量灰色马尔科夫预测

2 实例分析

2.1 数据来源及评价标准

通过对郑州市地铁站点客流量的分析，可以更好地规划城市地铁线路，促进城市快速发展。以郑州地铁2号线的14个站点在上下班时段、非上下班时段数据为对象进行分析，见图2。

图2 郑州市地铁2号线部分运行站点

为了更好地对客流量预测结果进行评价，采用均方根误差Ems和平均相对误差Em进行衡量，Ems和Em的计算公式为[7]:

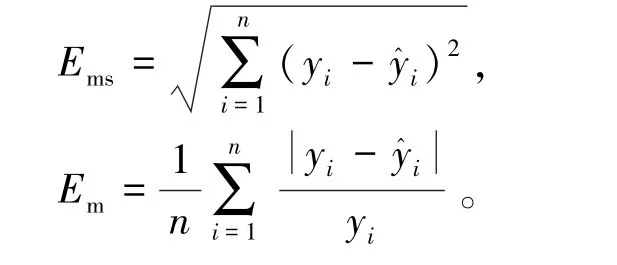
式中:y=[y1，y2，…，yn]为地铁站点客流量；=[，，…，]为地铁站点预测客流量。

2.2 预测结果分析

对郑州地铁2号线上下班时段客流量数据(7∶00—8∶30时段和17∶00—18∶00时段客流量数据的平均值)进行预测，结果如图3所示。

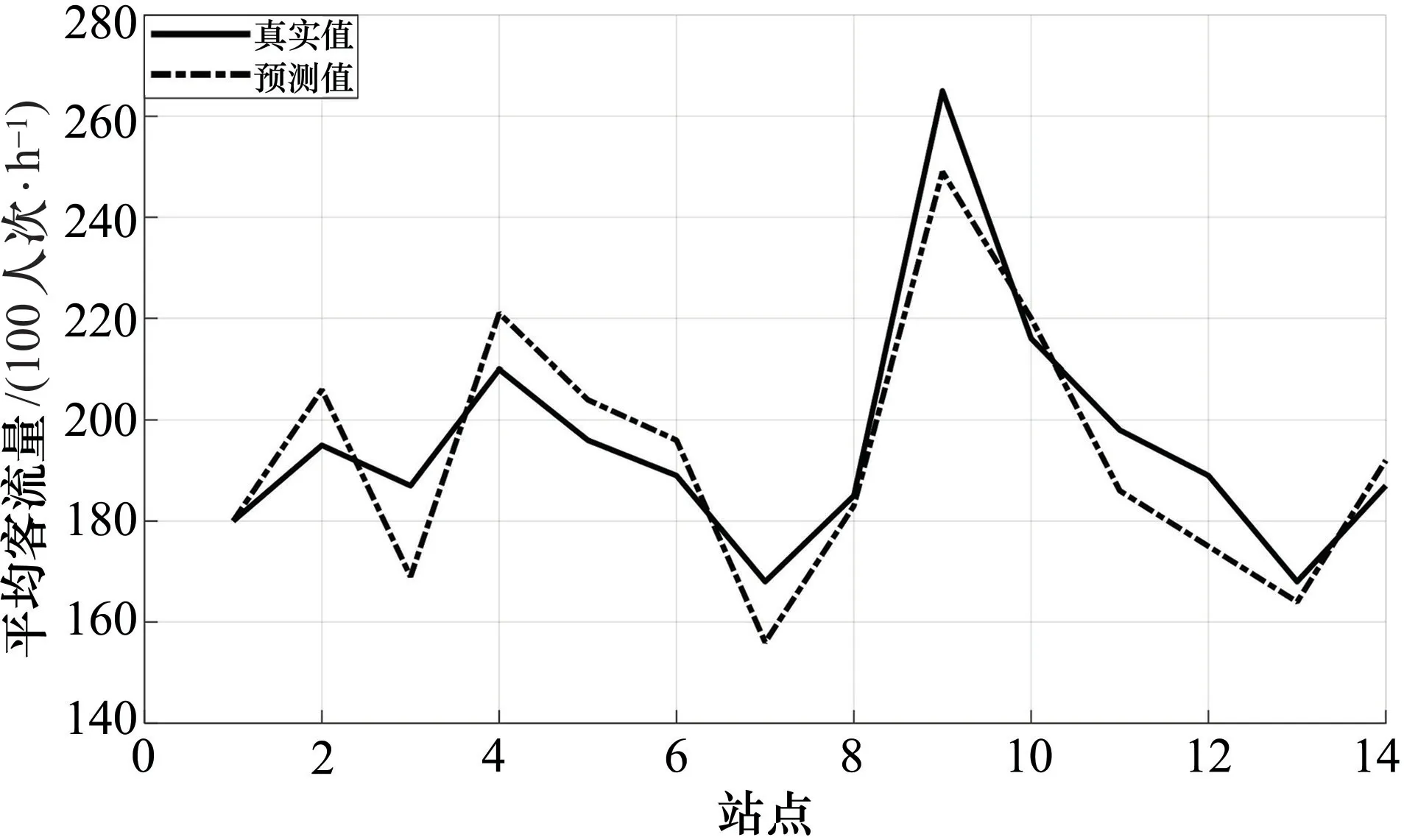
图3 上下班时段客流量

由图3可知，地铁2号线上下班时段的第9个站点平均客流量最大，第7个站点平均客流量最小。第9个站点为沙门站，为换乘站，客流量比较大。第7个站点为刘庄站，所处位置住户比较少，地理位置相对比较偏僻，客流量比较小。

对郑州地铁2号线非上下班时段客流量数据(9∶00—11∶00时段和15∶00—16∶30时段数据的平均值)进行预测，结果如图4所示。

由图4可知，地铁2号线非上下班时段依旧是第9个站点平均客流量最大，第7个站点平均客流量最小，导致出现这种情况的原因同样也和站点所处的位置有密切的关系。

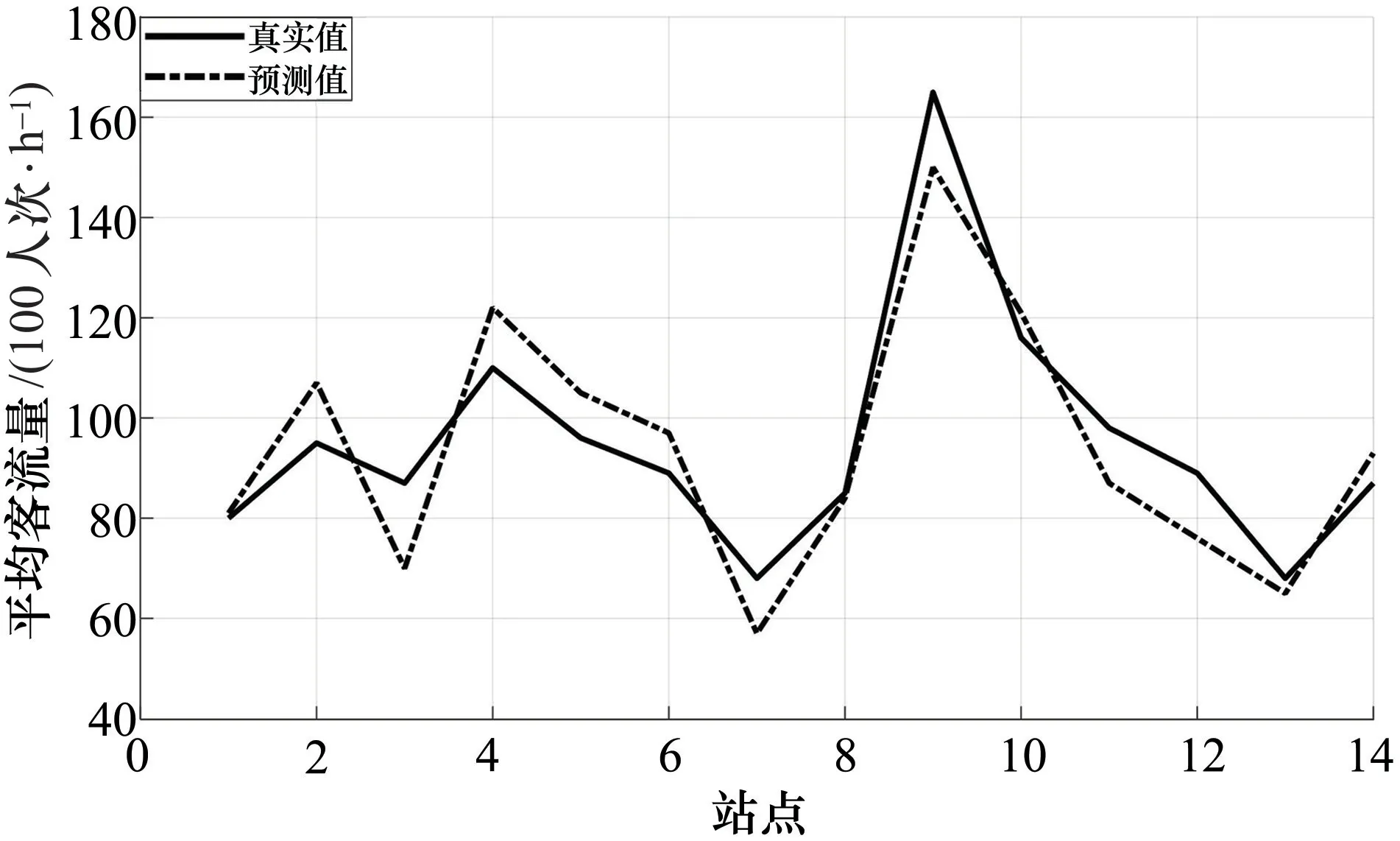
图4 非上下班时段客流量

为了衡量地铁2号线客流量预测的性能，计算均方根误差和平均相对误差，结果如表1所示。

表1 客流量预测结果评价

由表1可知，采用灰色马尔科夫预测模型进行预测时，上下班时段的Em为4.49%，非上下班时段的Em为9.33%，均小于10%，具有较高的预测精度。对非上下班时段客流量预测的误差比较大，是因为该时段客流量的随机性和波动性比较大。

3 结论

采用GM(1，1)模型进行预测，通过是否满足马氏性来科学选择残差向量傅里叶级数展开项，最终构建了轨道交通客流量灰色马尔科夫预测模型。将预测模型应用于郑州地铁2号线客流量预测中，结果表明对地铁2号线上下班时段以及非上下班时段的客流量预测平均相对误差均在10%以内，具有比较高的预测精度。