TRAVELING WAVES IN A SIRH MODEL WITHSPATIO-TEMPORAL DELAY AND NONLOCAL DISPERSAL*

Lu YANG(杨璐)Yun-Rui YANG(杨赟瑞)|Xue SONG(宋雪)

School of Mathematics and Physics，Lanzhou Jiaotong University，Lanzhou 730070,China E-mail: yanglu19910729@163.com; lily1979101@163.com; sac18604126839@163.com

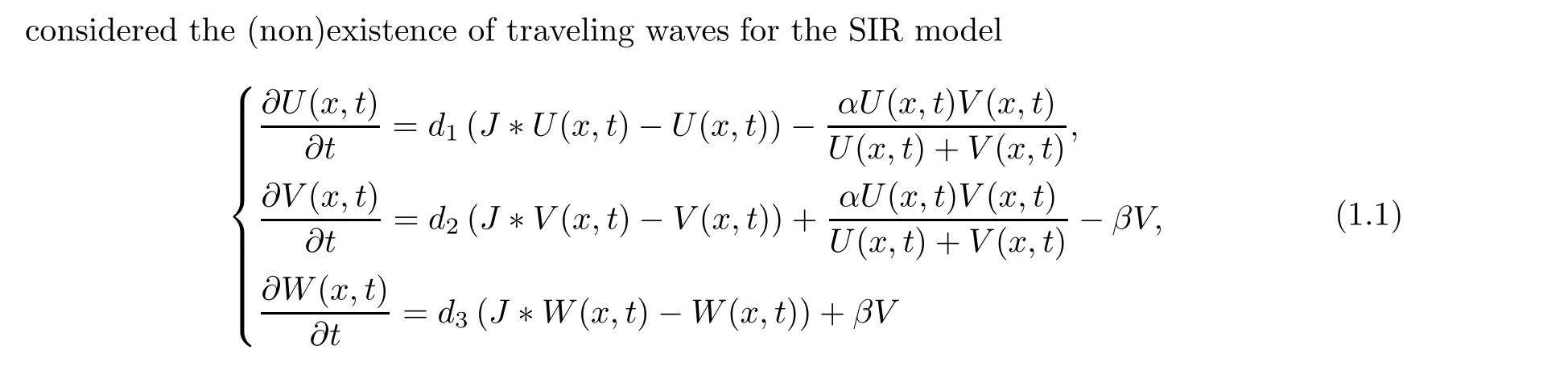
with nonlocal dispersal, where U, V and W are the densities of susceptible, infected, and cured individuals, respectively. di>0(i=1,2,3) indicates the dispersal rate, α represents the infection rate, and β denotes the recovery (treatment) rate.

On the other hand, time delay is actually inevitable for many phenomena in the real world,such as the latency period of bacteria, digestion periods, maturation periods of species and so on. Consequently, traveling waves of those models with nonlocal dispersal and delay have been extensively investigated [13-15]. In 2020, Yang et al. [15] established the (non)existence,boundedness and asymptotic behavior of traveling waves for the nonlocal dispersal SIR model

equipped with delay and nonlinear incidence. In addition,in view of the fact that every possible location of an individual in all previous times has an impact on the current state,Britton[16,17]and Smith [18] introduced what they called “time and space nonlocality”; namely, spatiotemporal delay by the idea of a spatial weighted average and a method of characteristic lines.Since then, the investigation of traveling waves for nonlocal dispersal equations with spatiotemporal delay has made great progress [19-24]. For example, by Schauder’s fixed theorem,together with a two-sided Laplace transform, Wang et al. [19] extended the (non)existence results for traveling waves of (1.1) to the model

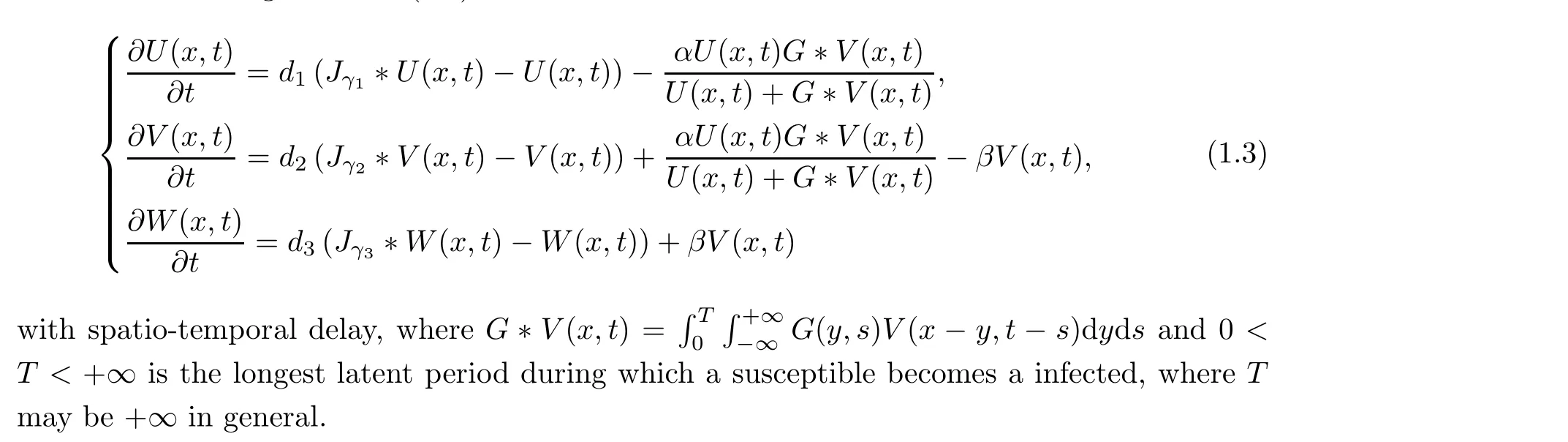
However,the above SIR models do not consider whether individuals who received treatment will be ill again or not, and therefore they are not realistic for describing infectious diseases with relapse, such as the flu, herpes, COVID-19 and so on. In 2017, Zhu et al. [12] put their emphasis on the SIRH model

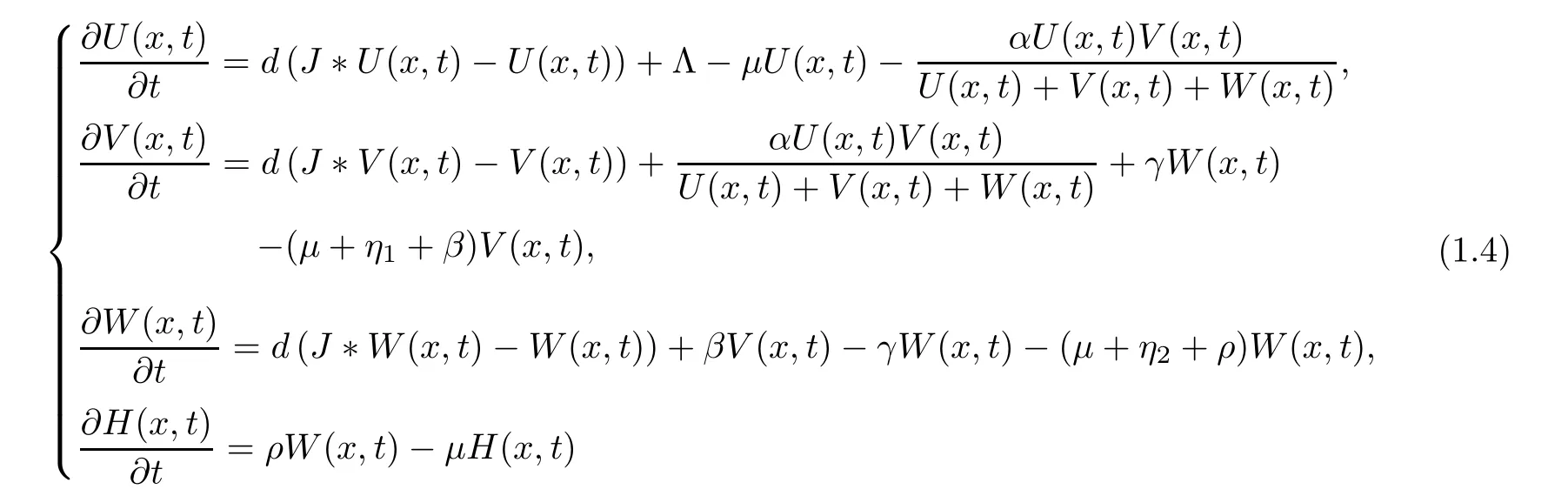
with relapse,where Λ is the external import rate,µrepresents the death rate,γ denotes the rate of relapse, ρ indicates the permanent immunity rate, and H(x,t) is the density of individuals who received treatment and will never relapse again. They established the (non)existence,boundedness and asymptotic behavior of the traveling waves of (1.4)by Schauder’s fixed-point theorem and analysis techniques. Notice that the effect of delay (that is, the latency period of bacteria) is not considered in the model (1.4).

As a result, based on the above works [11, 19, 22, 24] and motivated by the ideas of Wang[19] and Yang [24], we intend to generalize the above traveling wave results for (1.4) to the model

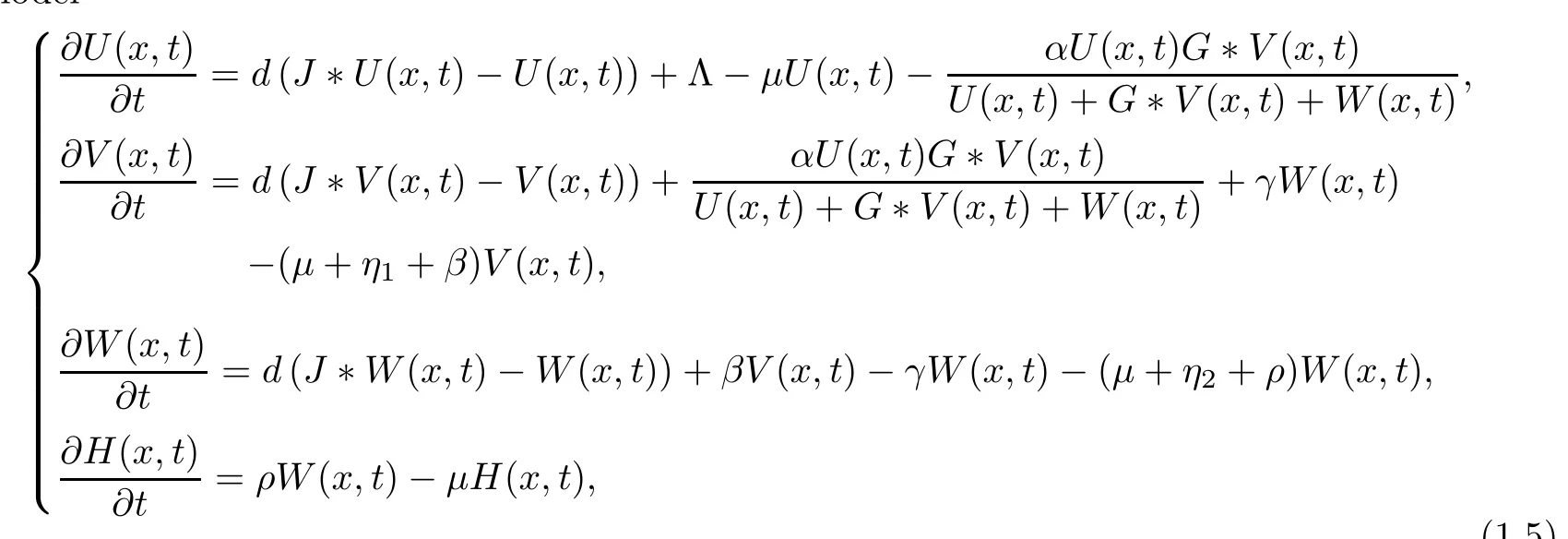
with relapse and spatio-temporal delay. First, we will find a positive constant c∗, which will be defined later (Lemma 2.1), to construct the existence and asymptotic behavior of the positive bounded traveling waves of (1.5) for c > c∗by Schauder’s fixed-point theorem, analysis techniques and integral techniques. It should be pointed out that we need the same diffusive rates and natural morality rate for U,V and W to guarantee the boundedness of traveling waves.There is a certain difficulty in establishing the asymptotic behavior of traveling waves for (1.5)with c>c∗by the previous method in[12]for the appearance of spatio-temporal delay. Inspired by the work of Yang et al. [24], this difficulty is overcome by the use of integral techniques and analysis techniques. In addition, the existence of non-negative bounded traveling waves with c = c∗is also obtained by the limit theory. In particular, motivated by the ideas of Yang et al. in [11], the existence and asymptotic behavior of positive bounded traveling waves of (1.5)when c = c∗and γ = 0 are proven by some analysis techniques, and this improves upon the work of Wang et al. [19] and Zhu et al. [12]. Finally, we also find another positive constant c∗,defined in Lemma 2.1, to establish the nonexistence of traveling waves of (1.5) with 0 ＜c ＜c∗by a two-sided Laplace transform, which is different from the method of Yang et al. [24], who only obtained that there is no traveling wave solution decaying exponentially at ξ →-∞, we obtain more general nonexistence results.

It is worth noting that the two positive constants mentioned above, c∗and c∗, satisfy 0 ＜c∗≤c∗; this is attributed to the fact that the rate of relapse and spatio-temporal delay arise at the same time in the model(1.5). It is still an open problem as to whether or not there is a traveling wave when c∗≤c ＜c∗for c∗＜c∗. Moreover, when the relapse and the healing individuals H(x,t) are not considered, and taking Λ = µ = γ = H = η1= η2= 0, the model(1.5) becomes a SIR model with spatio-temporal delay in [22]; when G(x,t) = δ(x)·δ(t), the model (1.5)reduces to (1.4), where δ(·) is Dirac function. Therefore, this paper generalizes the conclusions in [12, 19, 22].

The rest of this article is arranged as follows: in Section 2, some of the assumptions and preliminary results we need are illustrated. In Section 3,the existence,boundedness and asymptotic behavior of traveling waves for the wave speed c ≥c∗are established. In Section 4, the non-existence of traveling wave solutions for 0 ＜c ＜c∗is investigated.

2 Preliminaries

Considering the relative independence of the fourth equation in(1.5),it is sufficient to focus on the following system:

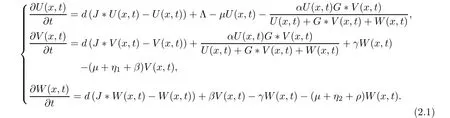
Denote the initial disease-free equilibrium as E:=(U0,0,0). Let(U(x,t),V(x,t),W(x,t))=(U(ξ),V(ξ),W(ξ))and ξ =x+ct. Then(U(ξ),V(ξ),W(ξ))satisfies the corresponding traveling wave system of (2.1) as follows:

The following results are consequently deduced:

Lemma 2.1 Supposing that (A1)-(A3) hold, then a positive constant c∗can be found to ensure that △(λ,c) = 0 admits only real roots when c > c∗. In particular, there is some positive number δ small enough satisfying △1(λc+δ,c)＜0 and △2(λc+δ,c)＜0 if λcindicates the first positive root of △(λ,c)=0. In addition, another positive constant c∗can be found to guarantee that there exists only one positive real root of △(λ,c)=0 when 0 ＜c ＜c∗.

呈现译本乃译者与作者、读者之间交互作用的实践结果，呈现译本的可接受程度取决于译者交互隐形的程度。随着交互层次的梯升，译者完成三级交互后自身最终消解于理解场和阐释场，这正是译者隐形的本质所在。随着翻译研究向多领域、跨学科不断发展，借助哲学视角全面解读译者隐形的内涵，明确其衡量译本呈现及效果的尺度价值，从而避免因译者认知偏差而过度显形所造成的译本失真呈现。

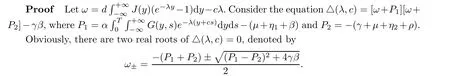
Consequently, △(λc,c) = 0 for some λc> 0 and c > c∗, where λc∈(λ-1,λ+1) and λcis the first positive root of △(λ,c) = 0. Therefore, there exists some δ > 0 small enough such that△1(λc+δ,c)＜0 and △2(λc+δ,c)＜0, due to the fact that △1(λ,c), △2(λ,c) and △(λ,c) are all continuous. The proof is complete. □

Remark 2.2 For 0 ＜c ＜c∗,there is no real root for one of △1(λ,c)=0 and △2(λ,c)=0,at least.

3 Existence of Traveling Waves

In this section, we first investigate the existence and asymptotic behavior of positive bounded solutions for (2.2) with c > c∗. Second, the existence of non-negative bounded solutions for (2.2) with c=c∗is obtained. Also, the existence and asymptotic behavior of positive bounded solutions for (2.2) with c=c∗and γ =0 are included.

3.1 Traveling waves for c>c∗

In order to establish the existence and asymptotic behavior of positive bounded solutions of (2.2) for c>c∗, the following lemmas are needed:

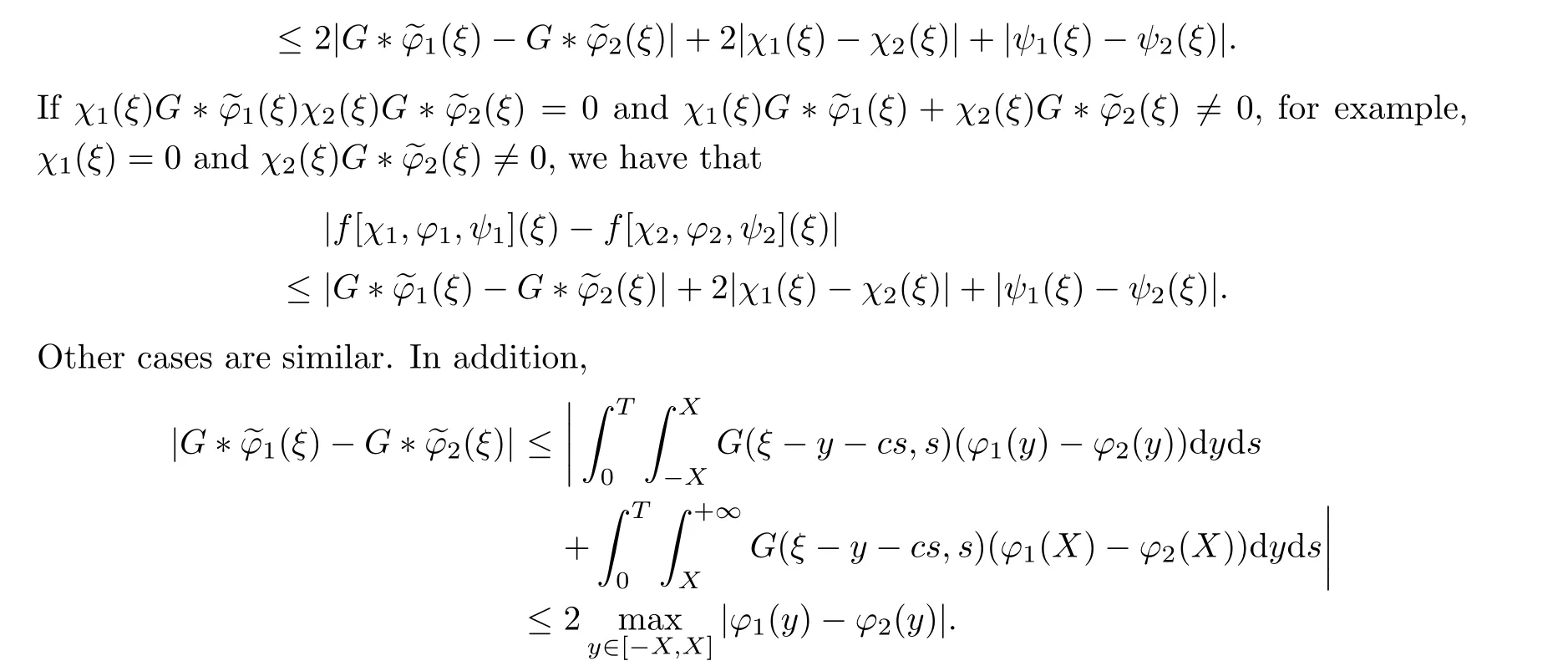
In conclusion, the above discussions lead to

Naturally, (3.5) has a unique solution UX(·),VX(·),WX(·)∈C1([-X,X]), by the ODE theory.Now, an operator F =(F1,F2,F3) on ΓXis defined as

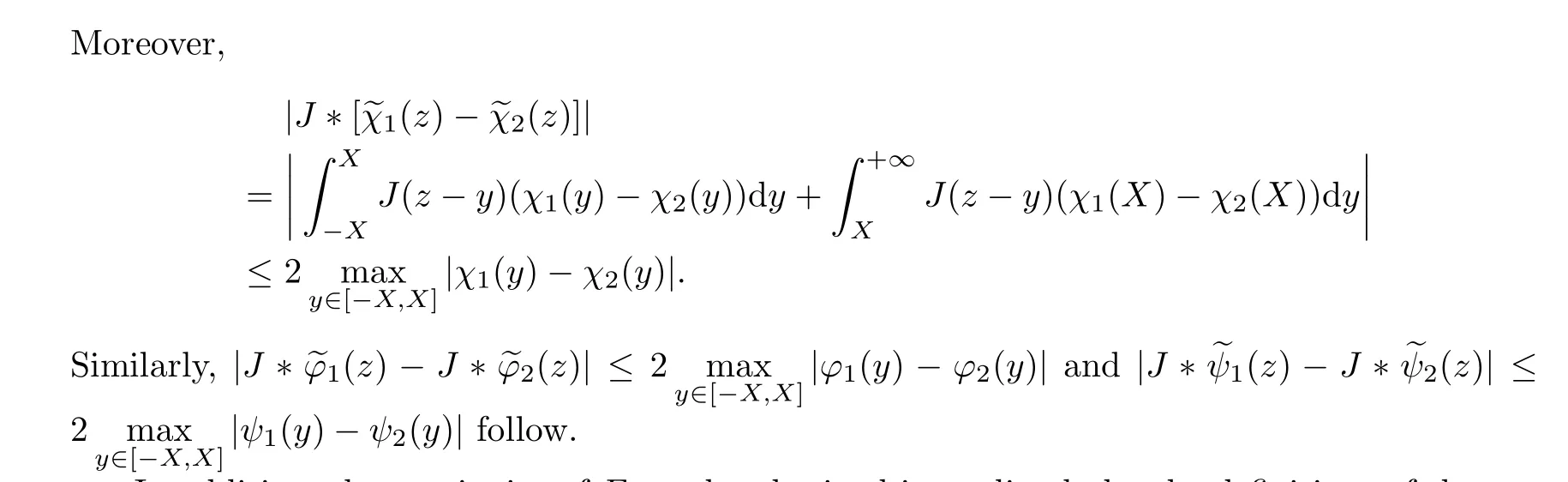
In addition, the continuity of F can be obtained immediately by the definitions of the operators UX,i(·),VX,i(·),WX,i(·) and F. Furthermore,U＇X(ξ), V＇X(ξ) and W＇X(ξ) are all bounded for ξ ∈[-X,X], (χ(·),φ(·),ψ(·)) ∈ΓXby (3.5), and UX(·),VX(·),WX(·) are all C1([-X,X]),which implies that F is relatively compact on ΓX. Therefore, F is a completely continuous operator. The proof is complete. □

Obviously, ΓXis a bounded and closed convex set. It follows from Schauder’s fixed-point theorem that there exists (UX(ξ),VX(ξ),WX(ξ))∈ΓXsatisfying

Theorem 3.8(Existence) Assume that(A1)-(A3)hold. Then there is a bounded solution(U(ξ),V(ξ),W(ξ)) of (2.2) satisfying 0 ＜U(ξ)＜U0, V(ξ)>0, W(ξ)>0 for every c>c∗.

Proof In light of the above discussions,we only need to show that 0 ＜U(ξ)＜U0, V(ξ)>0, W(ξ)>0 for ξ ∈R.

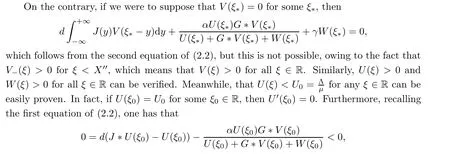
which leads to a contradiction. Therefore, U(ξ)＜U0for any ξ ∈R. The proof is ended. □

Next, we demonstrate the asymptotic behavior of positive bounded solutions of (2.2) for c > c∗; that is, we prove the solutions (U(ξ),W(ξ),V(ξ)) of (2.2) in Thoerem 3.8 satisfying(2.3) and (2.5) when γ > 0, or satisfying (2.3)-(2.4) when γ = 0. For the proof, the following assumption (A4) is also needed when γ =0:

(A4) G is compactly supported with respect to the space variables, and RGis the radius of the compact support set of G with RJ≥RG.

3.2 Traveling waves for c=c∗

In this subsection, the existence and asymptotic behavior of solutions of (2.2) for wave speed c=c∗are investigated. It is easy to verify that(2.1)admits a unique positive equilibrium E∗:=(U∗,V∗,W∗)when γ =0 and(A3) holds, where U∗>0,V∗>0,W∗>0. For the proof,the following result is necessary:

Lemma 3.10 Assume that (A1)-(A3) hold. Then, for every c > c∗, both U(+∞) and W(+∞) exist, and (U(ξ),V(ξ),W(ξ)) satisfies (U(+∞),V(+∞),W(+∞)) = E∗if γ = 0,α>b(c) and V(+∞) exists.

Theorem 3.11 Assume that (A1)-(A3) hold. Then, for c = c∗and γ ≥0, there is a bounded solution(U(ξ),V(ξ),W(ξ))of (2.2)satisfying 0 ≤U(ξ)≤U0, V(ξ)≥0 and W(ξ)≥0

Remark 3.12 The existence and asymptotic behavior of positive bounded traveling waves with c=c∗for γ =0 can be included in Theorem 3.11. However,the existence and asymptotic behavior of positive bounded traveling waves with c=c∗for γ >0 are still open questions.

4 Nonexistence of Traveling Waves

In this section, we intend to establish the nonexistence of solution of (2.2).

5 Numerical Simulation and Discussion

Theorem 3.8, Theorem 3.11 and Theorem 4.1 provide a threshold condition for whether the disease spreads or not. Specifically, according to Theorems 3.8 and 3.11, if c ≥c∗and(A1)-(A3) hold, then there are traveling waves for(2.1). In addition, by Theorem 4.1 there are no traveling waves for (2.1) when 0 ＜c ＜c∗and (A1)-(A3) hold. Furthermore, we show that the wave speeds c∗and c∗are influenced by diffusion and time delay. In fact, it follows from Lemma 3.1 that

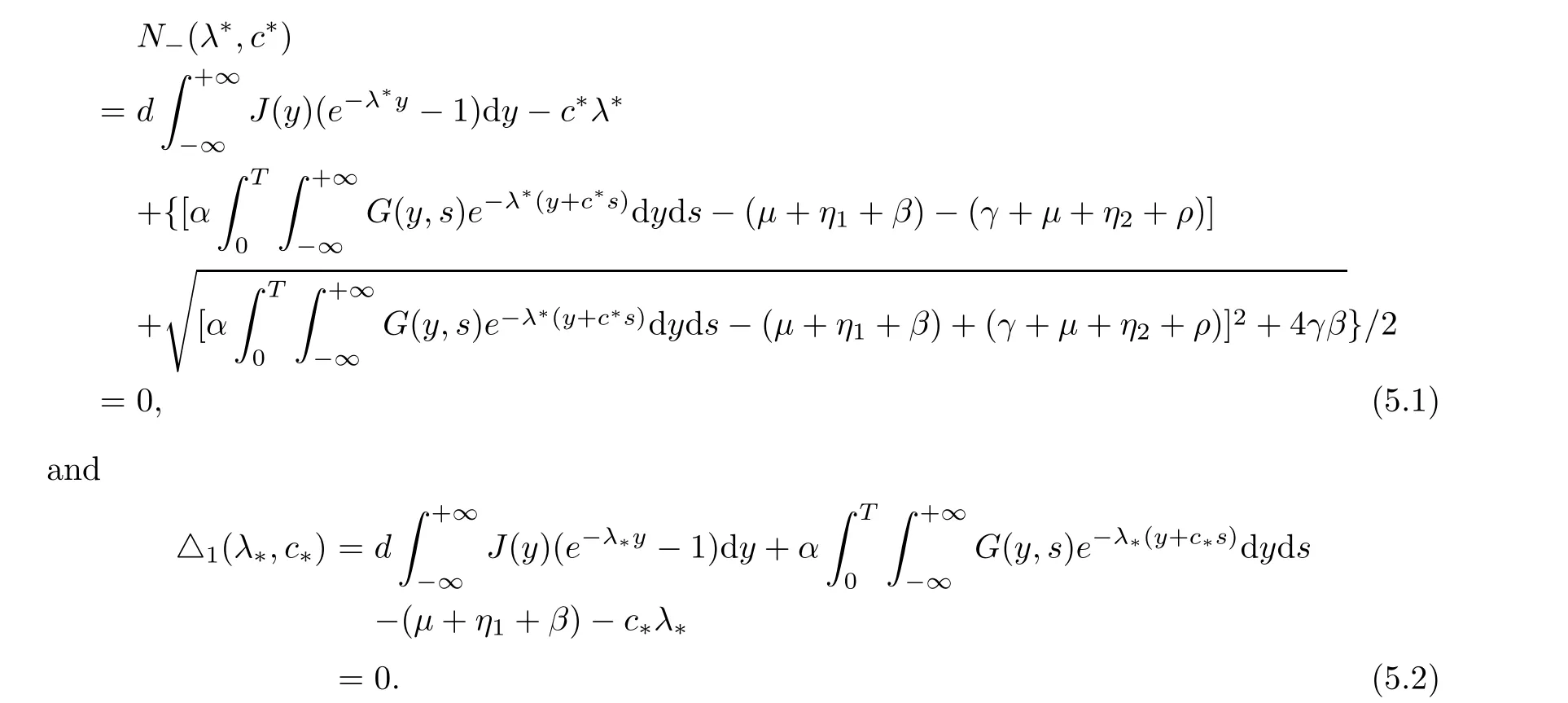
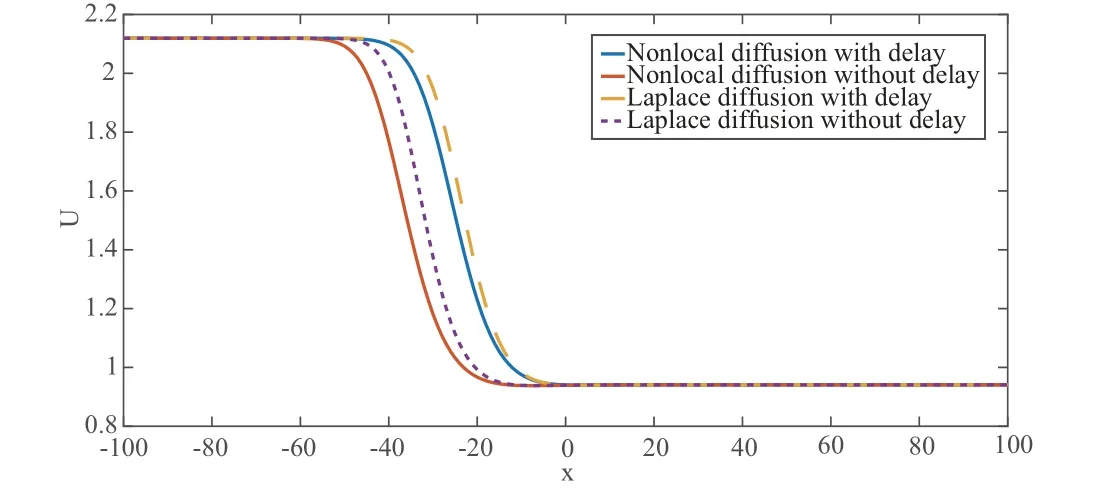
Figure 1 Traveling waves of U

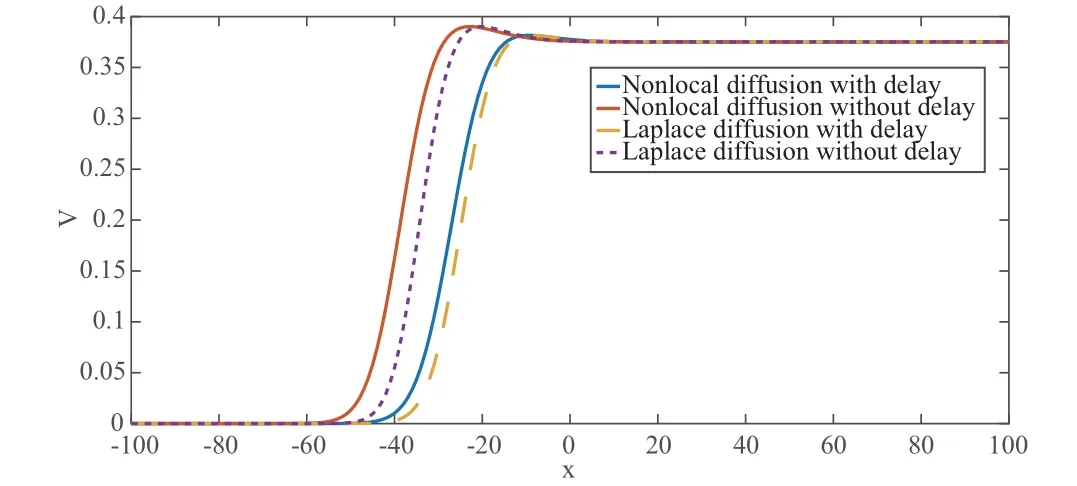
Figure 2 Traveling waves of V

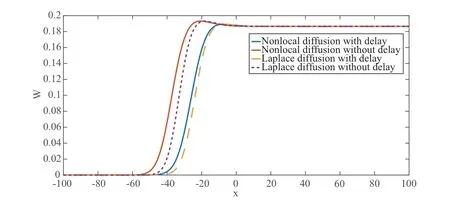
Figure 3 Traveling waves of W

On the other hand, inspired by the work of Zhu et al. [12], the two-dimensional numerical simulations for traveling waves of an HIV/AIDS infection model with (or without) delay and local (or nonlocal) dispersal are demonstrated above (in view of the fact that the HIV/AIDS infection model is well-known, and as a kind of epidemic model with relapse).

In the process of numerical simulation, d = 0.1, and the other correlation parameters are stated in the table below.

?

In addition, U0= 2.119122257, U∗= 0.9407872997, V0= 0, V∗= 0.3752146776, W0= 0 and W∗=0.1865579503 can be obtained by a simple calculation.

As is shown in Figures 1-3, the spread of traveling waves can be accelerated by nonlocal dispersal, while it can be slowed down by time delay, that is, in biology, disease spread will be faster in the case of nonlocal dispersal and small time delay. This conforms with the above discussions in mathematical analysis.

AcknowledgementsWe would like to give thanks for the help in numerical simulations to doctoral student Mingzhen Xin of the School of Mathematics and Statistics at Lanzhou University.