a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *

Yiming DING (丁义明)+Yun SUN(孙运)

Center for Mathematical Sciences，School of Science,Wuhan University of Technology,Wuhan 430070,China E-mail : dinggm@whut.edu.cn; sungun@whut.edu.cn

Definition 1.1 An indecomposable compact invariant set A ⊆X is called a topological attracting set if int(B(A)) /= ∅, where B(A) = {x ∈X,ω(x) ⊆A} is its basin of attraction. A topological attractor is a topological attracting set which contains a dense orbit.

From Definition 1.1, a topological attracting set A is indecomposable and invariant, and it attracts a non-empty open set. In what follows, we call A an attracting set for brevity.Note that an attracting set may admit empty interior (for example, an attracting fixed point).The basin of attraction follows from Milnor’s definition of metric attractor [21], and that A is indecomposable follows from Williams [27]. The attracting set A must be indecomposable,because the number of attracting sets may be large if A is decomposable. For instance, if attracting set can be decomposable,then the union of A and a repelling periodic orbit can also be an attracting set, so there will be too many attracting sets. A topological attractor contains a dense orbit, which indicates that f is topologically transitive on the topological attractor,and we call it an attractor for brevity.

Denoting Afas the collection of all attracting sets of f, in this paper we shall consider a family of maps F. For f ∈F, f admits unique attractor A and satisfies the following two conditions:

• Basin condition: ∀Ai,Aj∈Af, if int(B(Aj)△B(Ai))=∅, then Aiand Ajare nested.

• Finiteness condition: ∀M ∈AfA, #{E ∈Af,E ⊇M}＜∞.

For any f ∈F, f has only one topological attractor. The topological behaviors could be complicated when attractor is not unique. ∀Ai,Aj∈Af, that Aiand Ajare nested implies that Ai⊇Ajor Aj⊇Ai. The basin condition indicates that(B(Aj)B(Ai))∪(B(Ai)B(Aj))is nowhere dense, which is used to prove that the attracting sets are nested; see Lemma 2.1 for details. The finiteness condition is a technical condition, which will be used to ensure the existence of maximal proper attracting set if f ∈F is not transitive. If f has only finite attracting sets, the finiteness condition is satisfied automatically. If f has infinite attracting sets,the finiteness condition implies that for any attracting set of f which is not the topological attractor, there are finite number of attracting sets of f which contain it. According to [9, 10,16],if f is either a topologically expansive Lorenz map,or a unimodal map without homterval,it admits unique topological attractor and satisfies those two conditions. It is interesting to know whether there exists continuous map in compact metric space with one topological attractor and violating the finiteness condition.

Isolated invariant sets (see Definition 4.3) are singled out because they can be continued to nearby systems in a natural way, and in this sense they are stable objects. Conley [5]obtained the fundamental decomposition theorem of isolated invariant sets and extended it to Morse decomposition. Since then the Conley index theory had been studied extensively[2, 18, 20, 26]. Liu [20] studied the Conley index for random dynamical systems, and Wang[26] studied the shape Conley index in general metric spaces. Conley’s work focused on flow or homeomorphism,while we adapt the main ideas to a general continuous map. In this paper,we consider the topological behaviors of f ∈F on compact metric space X. We first introduce the A-R pair decomposition of X and obtain the leveled A-R pair decomposition of X,then use it to characterize α-limit set of each point. Observing that proper attracting set and corresponding repelling set could be intersected, but the interior is always disjoint, we prove that they are both isolated invariant sets when they are not intersected. In Section 4, we slightly modify the definition of Morse sets and obtain the weak Morse decomposition of X. Based on weak Morse decomposition, we construct a bounded Lyapunov function V(x), which can give a clear description of orbit behavior of each point in X except a meager set.

The remain parts of the paper is organized as follows: we introduce leveled A-R decomposition of X in Section 2, and characterize the α-limit set of each point in Section 3. In Section 4,we introduce weak Morse sets and obtain a bounded Lyapunov function V(x) via weak Morse decomposition of X. Although we characterize the topological properties of α-limit sets of f ∈F, the metric properties of such sets are not clear. Under some regularity conditions, it is still unknown if the α-limit set is of (Lebesgue) measure zero. For maps with more than one attractor, the topological characterizations of α-limit sets are still unclear.

2 Leveled A-R Pair Decomposition

Conley [5] obtained the attractor-repeller pair decomposition of isolated invariant sets, but some sets may be decomposable even if they are not isolated invariant sets, such as the whole space X. For f ∈F, we first introduce the A-R pair decomposition of X. According to Definition 1.1, if A is an attracting set, then int(B(A)) /= ∅. Let the dual repelling set of attracting set A be

Notice that A and R may be intersected at the boundary, but the interior is always disjoint.Denote L:=A ∩R and (A,R) as an A-R pair decomposition of X, then

Topological transitivity is a classical topological property. Let A be the unique attractor.Then f confined on A is topologically transitive, A is indecomposable and A contains a dense orbit. For any f ∈F, we first see whether it is topologically transitive on the X or not. If f is topologically transitive on X, then the whole compact space X is indecomposable and itself is a topological attractor. In this case, A=X, R=∅.

Lemma 2.1 Supposing that f ∈F, we have the following:

(1) If f is not transitive on X, then it admits a maximal proper attracting set A1.

(2)The proper attracting sets of f can be ordered as A1⊃A2⊃...⊃Am(0 ≤m ≤+∞).

Case 1: If int(B(B∗)) = ∅, then there exists no attractor in B. Since each attracting set contains an attractor, there exists one attractor in AiB and AjB, respectively. Hence we obtain two different attractors, which contradicts with the uniqueness of attractor.

Case 2: If int(B(B∗)) /= ∅, int(B(Ai) B(B∗)) /= ∅and int(B(Aj) B(B∗)) = ∅, then there exists one attractor in AiB and B respectively, which contradicts with the uniqueness of attractor.

Case 3: If int(B(B∗)) /= ∅, int(B(Aj) B(B∗)) /= ∅and int(B(Ai) B(B∗)) = ∅, then there exists one attractor in AjB and B respectively, which contradicts with the uniqueness of attractor.

Case 4: If int(B(B∗))/=∅, int(B(Ai)B(B∗))/=∅and int(B(Aj)B(B∗))/=∅, then there exists one attractor in AiB , AjB and B respectively, which contradicts with the uniqueness of attractor.

Case 5: If int(B(B∗)) /= ∅, int(B(Ai)B(B∗)) = ∅and int(B(Aj)B(B∗)) = ∅, then both B(Aj)B(B∗) and B(Ai)B(B∗) are nowhere dense. Since B(B∗) = B(Ai)∩B(Aj), then B(Ai)B(Aj)=B(Ai)B(B∗) and int(B(Ai)B(Aj))=∅. Similarly, int(B(Aj)B(Ai))=∅.Hence(B(Aj)B(Ai))∪(B(Ai)B(Aj))is nowhere dense,which implies int(B(Aj)△B(Ai))=∅.Applying the basin condition, we can obtain that Ai⊆Ajor Aj⊆Ai. Since Aiand Ajare different attracting sets, Ai⊂Ajor Aj⊂Aiholds.

If f admits unique proper attracting set,then the maximal proper attracting set is attractor A. If f admits more than one proper attracting set,there exists a proper attracting set M ∈Afsuch that M ⊃A. By the finiteness condition, there are finite number of proper attracting sets which contain M. Let A1be the maximal proper attracting set which contains M. Given two proper attracting sets, we have proved that they are nested, and then all the proper attracting sets are nested. Hence A1is the maximal proper attracting set in Af.

(2) If f is not topologically transitive on X, we can obtain a maximal attracting set A1⊂X,A1is compact under the induced topology and A1is invariant under f. Denote f1:= f|A1and Af1as the collection of all attracting sets of f1. If f confined on A1has more than one attractor, then f|Xalso has more than one attractor since A1⊂X, which contradicts with the uniqueness of attractor. According to the definition of attracting set, we can obtain Af1=AfX, i.e., Af1⊂Af, then the finiteness condition and basin condition obviously hold for f1. Hence f1∈F and(A1,f1)is a dynamical system. If f1is topologically transitive on A1,then A1is the unique attractor of f. If f1is not topologically transitive on A1, there exists a proper maximal attracting set A2⊂A1, and f2is also a map in F. In this way, if fm-1is not transitive on Am-1,one can obtain the maximal attracting set Amof the system(Am-1,fm-1).Then we obtain a cluster of attracting sets ordered as follows: X =A0⊃A1⊃A2⊃...⊃Am,and m might be infinite. □

Let m be the level of dynamical system (X,f) if the process above can proceed m times consecutively. The level of(X,f)can be used to understand the relationship between attractor and attracting set. Denoting A0:=X, if m is finite, Amis the unique attractor since Amcan not be decomposed; if m is infinite, attractor is the intersection of all attracting sets.

Definition 2.2 If the level of(X,f)is m,since each attracting set corresponds a repelling set, there exist m proper attracting sets and m corresponding repelling sets. And the set of all (Ai,Ri) (0 ≤i ≤m) is called the leveled A-R pair decomposition of X, denoted as

{(A1,R1),(A2,R2),...,(Am,Rm)}.

Example 2.3 Let f : I = [0,1] →I be an m-renormalizable topologically expansive Lorenz map and c be the critical point. We regard the critical point c as two points c+and c-, then f is continuous in some sense since f is topologically conjugate to a continuous map on symbolic space [17]. According to [10], define Rf to be the minimal renormalization map of f and define [a1,b1] to be the renormalization interval, then Rf confined on [a1,b1] is also an expansive Lorenz map. Suppose that E1is the minimal proper completely invariant closed set corresponds to the minimal renormalization, i.e., f(E)=f-1(E)=E. Putting

3 α-Limit Set of Each Point

We prove that proper repelling sets and proper α-limit sets are the same sets from different aspects, and we characterize the α-limit set of each point via leveled A-R pair decomposition of X. Notice that attracting set and repelling set may be intersected, hence we particularly describe the α-limit sets of intersection points.

Lemma 3.1 Let f ∈F and the level of (X,f)is m. Then the following statements hold:

(1) ∀x ∈X, α(x) is a bi-invariant closed set of f.

(2) Each proper repelling set is a proper bi-invariant closed set.

(3) Each proper bi-invariant closed set is a proper α-limit set.

then Riis a proper bi-invariant closed set. Notice that if there are m proper repelling sets of f, then the number of proper bi-invariant closed sets is exactly m.

Proof (1) By Lemma 3.1, we know that proper repelling set and α-limit set of f are the same sets in different aspects. If the level of (X,f) is m, then f has exact m proper α-limit sets. It follows from the proof of Lemma 3.1 that all the α-limit sets are defined as Ri={x ∈X,orb(x)∩int(B(Ai))=∅}, i=1,2,...m, and

(2) If L=∅, at first, we describe the set {x ∈X,α(x)=R1} where R1is the repelling set corresponding to the maximal attracting set A1.

Claim α(x)=R1if and only if x ∈A0A1=X A1.

By the proof of (1), R1is the minimal proper α-limit set of f. So α(x)⊇R1for all x ∈X.Denote fi:=f|Ai(0 ≤i ≤m) and D1=R2∩A1. For ∀x ∈D1, x also belongs to R2and A1;because f(A1)=A1and orb(x)∩int(B(A2)) =∅, we can obtain f(x)∈D1and f-1(x)∈D1.Hence D1is the minimal proper bi-invariant closed set of f1. It follows that D1∩R1=∅and D1⊂R2. If x ∈X A1, i.e., x /∈A1, and as A1is invariant under f, for any n ∈N we have f-n(x)∩A1= ∅, so α(x)∩A1= ∅, which indicates α(x)∩D1= ∅. Hence, α(x)R2and α(x)=R1.

On the other hand,for any x ∈A1,since α(x,f1)=α(x,f)∩A1,we see that α(x)⊇α(x,f1).By the minimality of D1, α(x,f1) ⊇D1for all x ∈A1, so α(x)∩D1/= ∅, which implies that α(x)/=R1for x ∈A1. The proof of the Claim is completed.

For 0 ≤i ≤m, let Aibe the ith proper attracting set of f, let Ribe the corresponding repelling set, and let Dibe the minimal proper invariant closed set of fi. By the Claim we know that α(x)=R1if and only if

For the case i = 2 ≤m, we consider the map f1. According to the Claim, we obtain that α(x,f2)⊇D2if and only if x ∈A1A2. It follows that α(x)=R2if and only if x ∈A1A2.

Repeat the above arguments, we conclude that α(x)=Riif and only if

If m ＜∞, and fmis topologically transitive on Am, α(x,fm)=Amfor all x ∈Am. Then we have that α(x,fm) ⊆α(x), and Am⊆α(x) for all x ∈Am. If α(x) /= X for any x ∈Am,then X α(x) is a bi-invariant open set since α(x) is proper bi-invariant closed, and there exists another attractor in X α(x), which contradicts with the unique attractor. Hence we can conclude that α(x)=X for all x ∈Am.

Remark 3.2 If L /= ∅, ∀x ∈Li, we have either α(x) = Rior α(x) = Ri+1. In fact,according to Theorem A, if regard x ∈Ai, α(x) = Ri+1; if regard x ∈Ri, α(x) = Ri. In this way, the α-limit sets of points in meager set L can also be characterized.

If m=0,then f is topologically transitive on X which implies that α(x)=X for any x ∈X,since X is the largest α-limit set, f admits exactly m+1 different α-limit sets.

4 Lyapunov Function

We first introduce the definition of isolated invariant set, and prove that both proper attracting set and proper repelling set are isolated invariant sets when they are not intersected.Then we define the weak Morse decomposition of X via leveled A-R pair decomposition and obtain a bounded Lyapunov function of f.

Definition 4.1 (Franks & Richeson[12]) Let f ∈F and then f :X →X is a continuous map; for any set N ⊂X we define InvmN to be the set of x ∈N such that there exists an orbit segment {xn}m-m⊂N with x0= x and f(xn) = xn+1for n = -m,...,m-1. We will call a complete orbit containing x a solution through x. More precisely, if σ : Z →N is given by σ(n)=xnand x0=x and f(xn)=xn+1for all n,we will call σ a solution through x. We define InvN as Inv∞N, the set of x ∈N, such that there exists a solution σ with {σ(n)}∞-∞⊂N and with σ(0)=x.

Note that from the definition it is clear that f(InvN)=InvN. The following basic property of InvN is trivial if f is one-to-one, and also holds for general continuous maps:

Proposition 4.2(Franks&Richeson[12]) If f is a continuous selfmap on compact metric space X, and N is a compact subset of X, then

Definition 4.3 A compact set N is called an isolating neighborhood if InvN ⊂intN.A set S is called an isolated invariant set if there exists an isolating neighborhood N with S =InvN.

Suppose that m is the level of (X,f). Notice that Aiand Rimay be intersected, i.e.,Ai∩Ri/= ∅(0 ≤i ≤m), but the interior is always disjoint. At this case, the isolating neighborhoods do not exist, so both Aiand Riare obviously not isolated invariant sets.

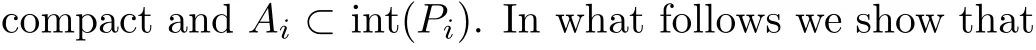
For instance, suppose that f is an m-renormalizable topologically expansive Lorenz map or an m-renormalizable unimodal map without homtervals.According to Example 2.3, if m is infinite, then both Aiand Riare isolated invariant sets for any 1 ≤i ＜m; if m is finite,then both Aiand Riare isolated invariant sets for 1 ≤i ≤m-1, but Amand Rmmay be intersected.

Conley put forward the decomposition of isolated invariant set that are consistent with concept of isolating neighborhood and obtained a Lyapunov function, which is called Conley’s fundamental decomposition theorem [5]. In fact, X is decomposable when f ∈F is not topologically transitive on X, but X is not an isolated invariant set since we can not find an isolating neighborhood N such that X ⊂intN. Hence,we slightly modify Conley’s fundamental decomposition theorem.

Now, V(x) -V(fn(x)) = 0 if and only if h(fm(x)) -h(fm+n(x)) = 0 for all m ≥0, i.e.,h(fm(x))=a constant for all m ≥0. This implies that ω(x)∩(A∪R)=∅,which contradicts with the definition of connecting orbits. Thus V(x)-V(fn(x))>0, and conclusion (3) holds.When A ∩R=∅, this implies L=∅and V(x) is defined on the whole space X. It is clear that g(x)and h(x)is continuous,hence V(x)is a continuous function, and conclusion(4)is verified.The proof is complete. □

Conley[5]extented fundamental decomposition theorem to Morse decomposition via Morse sets, and emphasized that Morse sets are disjoint compact invariant sets. However, when Aiand Ri(0 ≤i ≤m) are intersected, Aiis clearly not an isolated invariant set, but Aimay still be decomposable. Hence we slightly modify the definition of Morse sets and obtain the weak Morse decomposition of X via leveled A-R decomposition. Observe that weak Morse decomposition of X is more delicate, and this is almost the same as Morse decomposition of isolated invariant set when Ai∩Ri=∅for any 0 ≤i ≤m.

Definition 4.6 A weak Morse decomposition of X is a collection of interior disjoint compact invariant sets, called weak Morse sets,

Proof Observe that if m = 0, then MD= {M0= X} is the simplest weak Morse decomposition. When m = 1, the result MD= {M0= R1,M1= A1} is the same as Lemma

Now, V(x) -V(fn(x)) = 0 if and only if h(fm(x)) -h(fm+n(x)) = 0 for all m ≥0, i.e.,h(fm(x)) =a constant for all m ≥0. This implies that ω(x)∩MD= ∅, which contradicts with the definition of connecting orbits. Thus V(x)-V(fn(x))>0, and conclusion (4) holds.When L=∅and V(x)is defined on X. It is clear that g(x)and h(x) is continuous,hence V(x)is a continuous Lyapunov function, and conclusion (5) is verified.

As for(6),∀x ∈XL,we can obtain a value V(x)∈[0,1]. If V(x)=0,x ∈MmL=AmL and x belongs to the attractor, then according to Theorem A, α(x) = X. If V(x) = 1/2j(0 ≤j ≤m-1), then x ∈MjL, and according to Theorem A,α(x)=Ri+1. Furthermore, all the points in X MDare divided into m different connecting orbits. If V(x)∈(1/2j+1,1/2j),0 ≤j ≤m-1, then x ∈Cj. By the definition of connecting orbit, α(x)=Ri+1. Hence we can characterize the α-limit set of each point in X L via V(x). □

Let f be an m-renormalizable expansive Lorenz map or an m-renormalizable unimodal map without homtervals. If m is finite, Amis the topological attractor,and fmis topologically transitive on Am. According to Example 2.3, there exists possibility such that Am∩Rm/= ∅,but the interior is always disjoint. If Am∩Rm/= ∅, then V(x) of f is not continuous; if Am∩Rm=∅, then V(x) of f is continuous.