A NONSMOOTH THEORY FOR A LOGARITHMIC ELLIPTIC EQUATION WITH SINGULAR NONLINEARITY*
2023-01-09ChunyuLEI雷春雨
Chunyu LEI(雷春雨)
School of Sciences,GuiZhou Minzu University,Guiyang 550025,China E-mail: leichygzu@sina.cn
Jiafeng LIAO(廖家锋)+
College of Mathematics Education,China West Normal University,Nanchong 631002,China E-mail: liaojiafeng@163.com
Changmu CHU(储昌木)Hongmin SUO(索洪敏)
School of Sciences,GuiZhou Minzu University,Guiyang 550025,China E-mail: gzmychuchangmu@sina.com; gzmysxx88@sina.com

1 Introduction and Main Result
We study the existence of multiple positive solutions for the following logarithmic elliptic equation with singular terms:

Here Ω ⊂RN(N ≥3) is a bounded domain with a smooth boundary, 0 <γ <1 and λ is a positive constant.
Regarding the singular semilinear elliptic equation on a bounded domain, many papers have studied the problem

For the elliptic equation with logarithmic nonlinearity, we can refer to [17-26] and the references therein. In particular, [24] considered the following semilinear elliptic equation with logarithmic nonlinearity:

Here 0 <p <2∗and b ∈C(Ω).
Inspired by the above works, we study problem (1.1). Compared with problem (1.2), the logarithmic term u log u2is indefinite. Compared with problem (1.3), we consider the case of-1 <p <0 and discuss the existence of positive solutions. Thanks to the critical point theory for nonsmooth functionals, we prove that problem (1.1) has at least two positive solutions.

for any u ∈H10(Ω). The singular term leads to the fact that the functional I does not belong to C1(H10(Ω),R). The sign of the logarithmic integral term is indefinite, which brings about some difficulties in terms of studying the existence of positive solutions to problem (1.1). Our main result is as follows:
Theorem 1.1 Assume that 0 <γ <1. Then there exists Λ0>0 such that problem(1.1)has at least two positive solutions for any 0 <λ <Λ0.
2 Preliminaries
With the help of [27] and[28], we first recall some concepts adapted from the critical point theory for nonsmooth functionals, especially the concept of a concrete Palais-Smale sequence.We then prove the existence of the negative energy solution of problem(1.1)in the next section.
Let (X,d) be a complete metric space, and let f :X →R be a continuous functional in X.Denote by |df|(u) the supremum of δ in [0,∞) such that there exist r > 0 and a continuous map σ :Br(u)×[0,r] satisfying

for (v,t)∈Br(u)×[0,r].
A sequence {un} of X is called a concrete Palais-Smale sequence of the functional f if|df|(un) →0 and f(un) →c <+∞as n →∞. In this paper, however, we use another concept instead: the so-called concrete Palais-Smale sequence for the functional I. Since we are looking for positive solutions of problem (1.1), we consider the functional I defined on the closed positive cone P of H10(Ω); that is,

Here P is a complete metric space and I is a continuous functional on P. We now introduce the following definition: a sequence {un} of P is called a concrete Palais-Smale sequence of the functional I if |dI|(un) →0 and I(un) is bounded. The functional I is said to satisfy the concrete Palais-Smale condition at the level c if any concrete Palais-Smale sequence {un} with I(un)→c possesses a convergent subsequence.
It turns out that if |dI|(u)<+∞, then we have the following lemma:





By the arbitrariness of the sign of φ, we can deduce that(2.12)holds. The proof of Lemma 2.3 is complete. □
3 Proof of Theorem 1.1
In this section, we first prove that problem (1.1) has a negative energy solution.
Lemma 3.1 There exist constants r,ρ,Λ0>0 such that the functional I satisfies
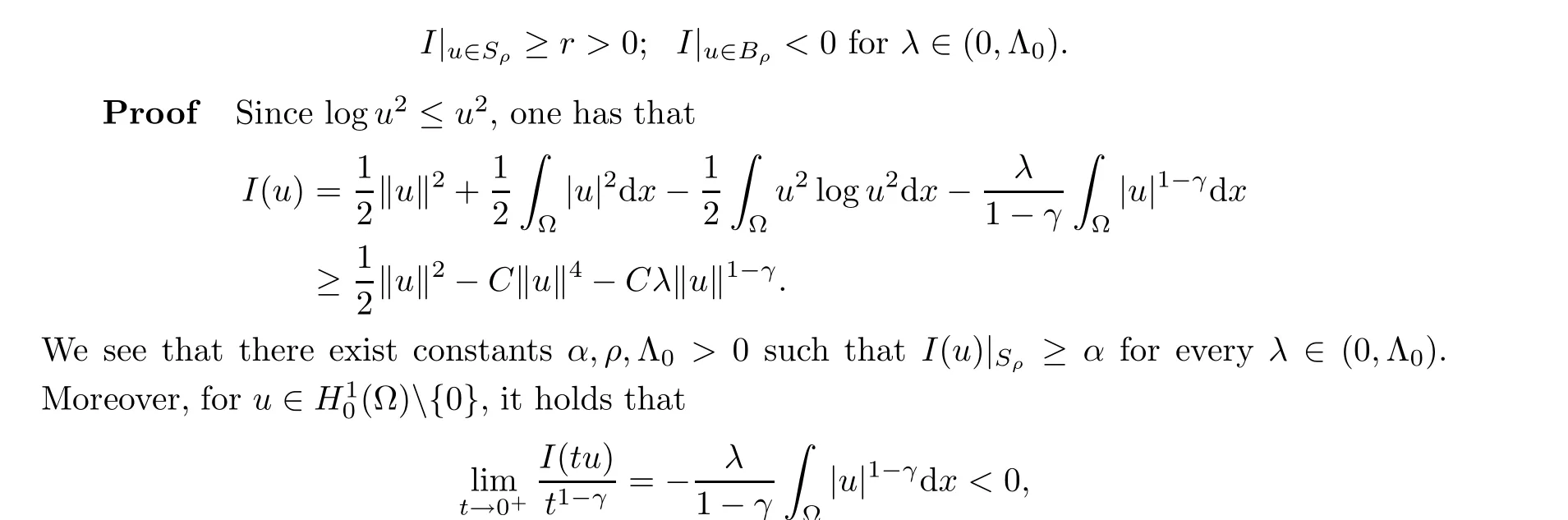
which implies that I(tu)<0 for t suitably small. Therefore, for ‖u‖ sufficiently small, one has that d ≜infu∈BρI(u)<0. The proof is complete. □
According to Lemma 3.1, we can obtain that d is attained at some u∗∈Bρ. Furthermore,by Lemmas 2.1 and 2.3, we obtain
Theorem 3.2 For 0 <λ <Λ0,problem(1.1)has a positive solution u∗with I(u∗)=d <0.

which implies that d ≥I(u∗). Since Bρis closed and convex, one has that u∗∈Bρ. Thus, we obtain that I(u∗)=d <0 and u∗/≡0 in Ω.
Second, we prove that u∗is a nonzero and nonnegative solution of problem(1.1). From the information above,we know that u∗is a local minimizer of I. Then,for v ∈P and a sufficiently small t>0 such that u∗+t(v-u∗)∈Bρ, one has that I(u∗)≤I(u∗+t(v-u∗)). In a manner similar to the proof of Lemma 2.1, we obtain that

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
- GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*
- COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*
- UNDERSTANDING SCHUBERT'S BOOK (III)*
- a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *
- STRONG CONVERGENCE OF AN INERTIAL EXTRAGRADIENT METHOD WITH AN ADAPTIVE NONDECREASING STEP SIZE FOR SOLVING VARIATIONAL INEQUALITIES∗
