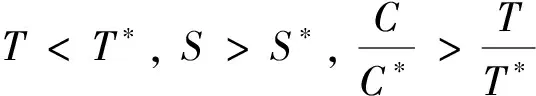对慢性感染者进行治疗的丙肝SICTR模型的全局性态分析
2023-01-09郑田田胡新利
郑田田, 胡新利
(西安工程大学 理学院,西安 710048)
0 引 言
全球丙肝病毒(Hepatitis C virus, HCV)感染者约7 100万人,每年新发丙肝病例300~400万例[1],其中约55%~85%的HCV感染者转为慢性肝炎,不及时治疗会逐步发展为肝纤维化、肝硬化甚至肝癌,这是严重危害人类健康的一个社会问题。随着DAA(Direct-acting antiviral agent)药物的问世,丙肝病毒的治愈率提升至95%以上[2],世界卫生组织提出2030年消除丙型病毒性肝炎这一公众卫生目标。但是因为丙肝病毒隐匿性强,发展速度慢,感染早期症状不易察觉,导致诊断率不足20%,治疗率更低。我国丙肝感染者约560万人,加上高危群体和高发地区人群,总计约1 000万左右[3]。因而对于世卫组织提出的目标还有很长的一段路要走。
近年来,数学模型被广泛用来分析丙肝病毒的传播和控制。文献[4]在经典宿主内丙型肝炎病毒感染模型中引入了一个肝外仓室,描述了宿主在肝内和肝外组织中感染丙型肝炎病毒的过程,得到了模型的全局动力学结果。文献[5]在文献[4]的基础上进一步考虑了免疫反应和CTL(Cytotoxic T lymphocyte)免疫应答对具有肝外感染仓室的丙肝模型的动力学分析。2017年,Zhang等提出并研究了一种新的乙型/丙型肝炎病毒感染数学模型,该模型考虑了健康肝细胞的增殖和被感染肝细胞的潜伏期,并证明了该模型的稳定性[6]。2008年,Keeling等考虑了一个具有两种传染状态的一般仓室模型,其中易感者能被急性感染者和病毒携带者所感染[7]。2011年,Martin等针对注射吸毒者提出了两种可能的治疗方案:每年治疗一定比例的感染者和每年治疗固定数量的感染者,并对这两种方案进行评估,给出了具有现实意义的方案[8]。2020年,Cui等提出了一个具有急性和慢性感染的丙型肝炎流行病学模型,强调急性丙型肝炎患者可以自行消除病毒进入康复类,而慢性丙型肝炎患者不能自动消除病毒进入康复类,并对该模型的全局动力学进行了研究[9]。2020年,Su等在研究中考虑到疾病传播过程中的个体空间扩散行为,提出了具有非线性感染率和HCV感染空间扩散的SICR模型[10]。尽管有大量学者对丙肝有了深入的研究,但是同时考虑丙肝的急、慢性期和治疗的文章较少。本文在文献[8-9]的基础上,根据丙肝的传播特点,建立了一个具有治疗策略的丙肝模型,并对该模型的全局动力学进行了研究。
1 模型建立
把疾病流行区域的整个人群N(t)分为5个仓室:易感者S(t)、急性感染者I(t)、慢性感染者C(t)、治疗者T(t)和恢复者R(t),并做出如下假设:
(1)人群是均质的,即所有人是混合均匀的,人口的输入率为Λ,且新输入的人口都是易感者;
(2)N(t)表示t时刻总人口数量,并且N(t)=S(t)+I(t)+C(t)+T(t)+R(t);
(3)由于近年来丙肝新药频现,且效果显著,因此不考虑在治疗过程中因病死亡的情况;
(4)易感者与急性感染者和慢性感染者之间的传染率相同,均为β。
根据丙肝的传播特点,给出了丙肝在人群中传播的流程图,如图1所示:
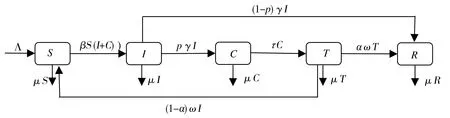
图1 丙肝传播流程图
根据图1,建立以下传染病模型:
(1)
其中Λ表示人口输入率;μ表示自然死亡率;β表示传染率;p表示急性感染向慢性感染的进展率,(1-p)表示急性感染者的自发清除率;γ表示急性感染者的移出率;τ表示接受治疗的慢性染病者的比率;α表示慢性感染者的治愈率;ω表示慢性感染者退出治疗的比率。
(2)
直接求解该方程,可得
易得
显然,
是系统(1)的正向不变集。由于变量R在系统(1)中前4个方程中没有出现,故只需研究前面4个方程,可以把系统(1)降维为如下系统:
(3)
接下来考虑系统(3)的动力学行为。
定理1系统(3)的有界正向不变集为
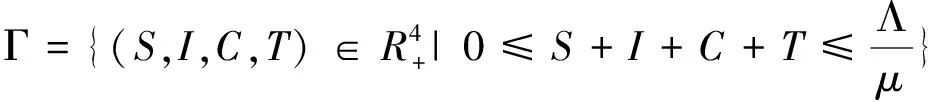
证明将系统(3)的各个式子相加,可以得到以下结果
(4)
由方程(4)得
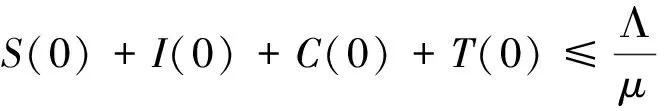
2 基本再生数和平衡点的存在性
(5)
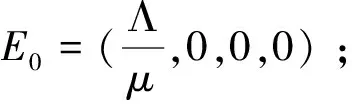
证明令系统(3)的右边等于0,得
(6)
由方程组(6)的后2个方程可得
(7)
将式(7)代入方程组(6)的第二个方程,得
(8)
将式(7)和式(8)代入方程组(6)的第一个方程中,得
(9)
因为R0>1,所以μ(τ+μ)(γ+μ)-βΛ(τ+μ+pγ)<0,又
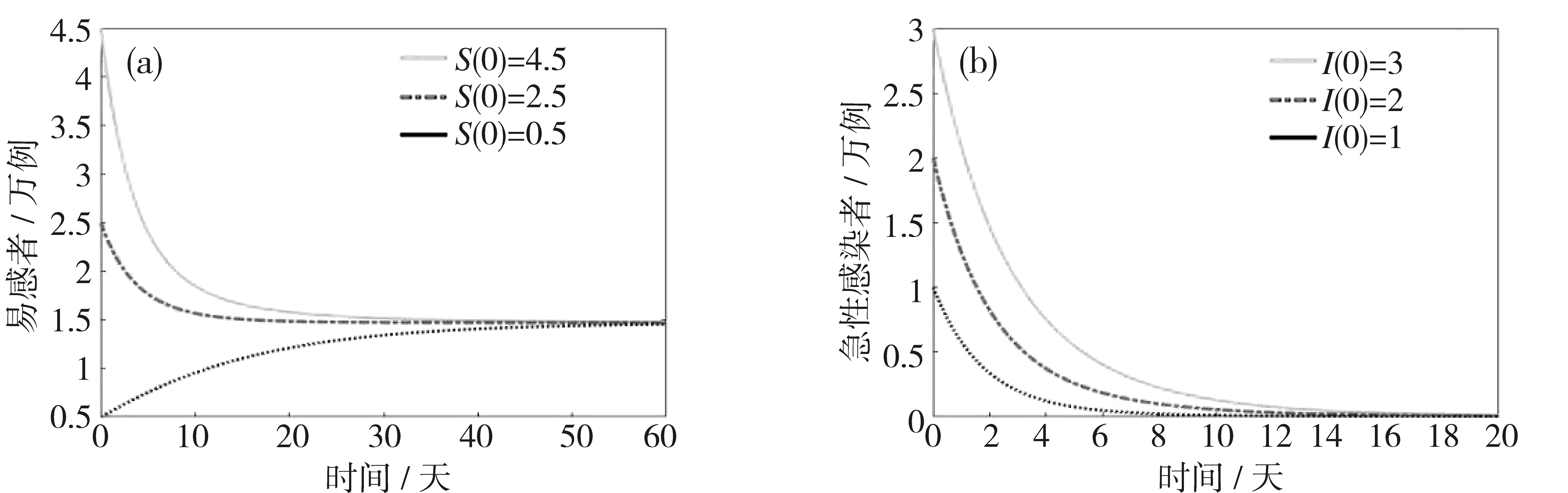
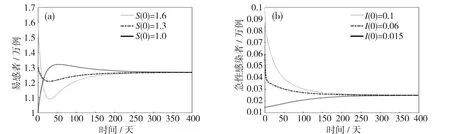
(γ+μ)(τ+μ)(ω+μ)>ωτγ>ωτpγ>(1-α)ωτpγ,0 所以C>0。 因此,当R0>1时,系统(3)除了无病平衡点外,存在唯一的地方病平衡点,记为E*=(S*,I*,C*,T*)。其中S*,I*,C*,T*均为正,且 定理3当R0<1时,系统(3)的无病平衡点E0在Γ内是局部渐近稳定的;当R0>1时,无病平衡点E0是不稳定的。 证明系统(3)在无病平衡点E0处的Jacobian矩阵为: 对应的特征方程为: 由特征方程可知λ1=-μ,λ2=-ω-μ,λ3,λ4满足方程: 此方程等价于 由一元二次方程的韦达定理,得 当R0<1时,显然得到λ3λ4>0,λ3+λ4<0,因此λ3<0,λ4<0。 由此可知,当R0<1时,所有特征根均具有负实部,系统(3)在无病平衡点E0处是局部渐近稳定的;当R0>1时,特征根具有正根,系统(3)的无病平衡点不稳定。证毕。 定理4当R0≤1时,系统(3)的无病平衡点E0在Γ内是全局渐近稳定的。 证明由定理3可知E0在Γ内是局部渐近稳定的,若要得到全局渐近稳定性,只需证明E0是全局吸引的。 构造Lyapunov函数: 对V1(t)关于系统(3)求全导数: 证明构造Lyapunov函数: 显然V2(t)在Γ中是正定函数。由方程组(6)可知 (10) 对V2(t)关于系统(3)求全导数,并将(10)代入,得 整理得 本节对系统(3)用数值方法来研究无病平衡点和地方病平衡点的稳定性和某些参数的敏感性,以及参数对慢性丙肝患者数量的影响。 图2中取参数β=0.024,τ=0.2,其他参数取值如表1所示。通过计算得R0=0.152 5<1,由定理3知无病平衡点是全局渐近稳定的。取初始值(S(0),I(0),C(0),T(0))分别为(4.5,3,2.5,0.5),(2.5,2,1.5,0.3)和(0.5,1,0.5,0.02)做数值模拟。从图2(a)~图2(d)中可以看出,所有的易感者随着时间的推移趋向于非零稳态(Λ/μ=1.47),急性感染者、慢性感染者和治疗者都随着时间的推移达到零稳态。 图2 R0=0.152 5<1时无病平衡点E0的全局稳定性 图3中取参数β=0.08,τ=0.015,其他参数取值如表1所示,计算可得R0=1.156 9>1,由定理4可知,存在一个稳定的地方病平衡点。取初始值(S(0),I(0),C(0),T(0))分别为(1.6,0.1,0.25,0.003),(1.3,0.06,0.15,0.002 5)和(1,0.015,0.09,0.001 6)作数值模拟。图3(a)~图3(d)显示所有的易感者、急性感染者、慢性感染者和治疗者都随着时间的推移达到非零稳态。 表1 系统(3)中参数的定义 图3 R0=1.156 9>1时地方性平衡点E*的全局稳定性 在图4和图5中取初始值为(S(0),I(0),C(0),T(0))=(1.5,1,0.8,0.16)。图4中取τ=0.015,β分别取0.06,0.08和0.1,其他参数取值如表1所示,可以看出最终的慢性丙肝感染者人数随β的增加而增加,要想控制丙肝,需要尽可能采取措施减少传染率。图5中取β=0.08,τ分别取0.01,0.03和0.05,其他参数不变,可以看出慢性丙肝感染者人数随τ的增加而减少,也就是增加对慢性患者的治疗率对于疾病的防控有着积极的意义。 图4 β对慢性丙肝患者数量的影响 图5 τ对慢性丙肝患者数量的影响 通过数值模拟的结果,分析易感者与染病者之间的传染率以及慢性丙肝患者的治疗率对慢性丙肝患者人数的影响,得出以下结论: (1)易感者与染病者之间的传染率越大,慢性丙肝患者人数就越多,当传染率达到一定值时,使得R0>1,丙肝将成为地方病;(2)丙肝治疗率越高,慢性丙肝患者就越少,当治疗率达到一定值,使得R0<1,丙肝将灭绝。因此,在应对丙肝传染病时,建议从两方面入手:第一,减少易感者与感染者的有效接触,例如避免共用一次性注射器和针头、严格消毒牙科器械和美容器械、发生高危性行为时使用安全套、妊娠前进行病毒学检查等;第二,提高丙肝治疗率:首先,丙肝治疗费用昂贵,虽然国家已经将治疗丙肝特效药纳入医保,但仍需关注贫困群体用药问题[16];其次,提高丙肝治疗率的重要环节是发现丙肝患者,这就要求人们做到:定期体检、出现全身乏力、食欲减退、恶心呕吐和肝区不适等症状及时就医,加大力度筛查有丙肝流行病史以及与丙肝病人密切接触的群体等。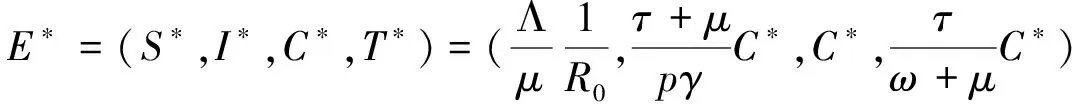
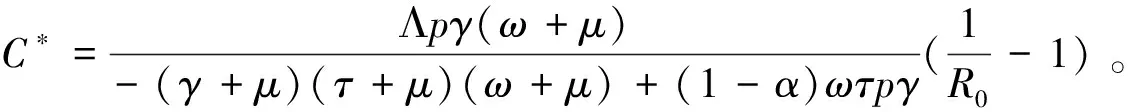
3 无病平衡点的稳定性
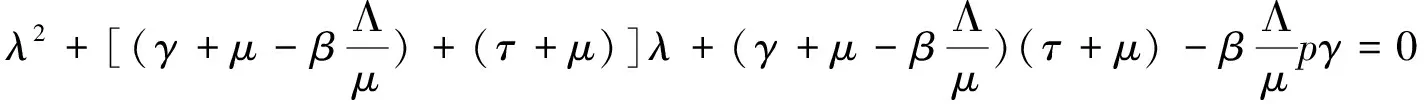
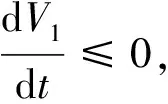
4 地方病平衡点的稳定性

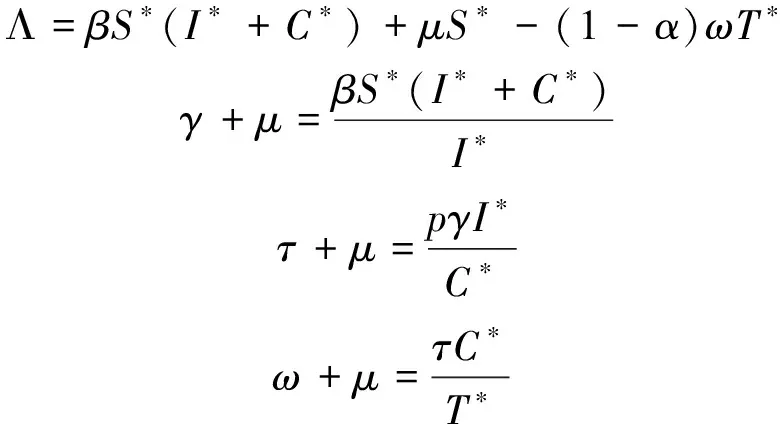
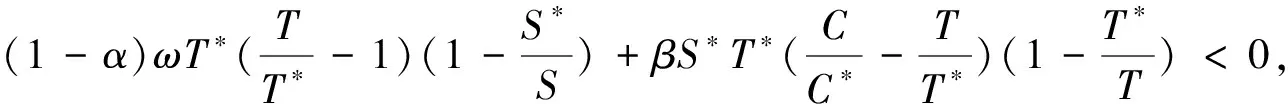
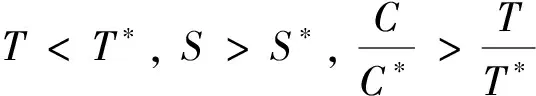
5 数值模拟



6 结论与建议