受媒体报道和疫苗接种影响的传染病模型分析

刘中凯，刘俊利，刘白茹

(西安工程大学 理学院，西安 710048)

传染病一直是影响人们身心健康和社会发展的重要因素，每年有成千上万的人死于传染病，所以对预防和控制传染病的研究具有重大意义. 随着科学技术的不断发展，媒体报道的信息对人们的生活产生了越来越重要的影响，而媒体报道对传染病的影响也越来越受到人们的关注. 通过媒体报道，可以提高人们的疾病防范意识，人们采取主动接种疫苗、佩戴口罩、主动隔离等措施，有效减轻了传染病的危害，阻碍了传染病的进一步传播.

文献[1]提出了一个带有媒体报道的传染病模型，加入了一个分段连续的传染率. 研究发现，如果感染的人数超过某一临界水平，那么媒体报道就会发挥积极作用. 文献[2]建立了一个非线性传染病模型，并且提出了一种估计媒体报道系数的新方法. 研究发现，媒体报道虽然不影响基本再生数，但是有助于降低疾病的危害，并且降低了在地方病稳定状态下的感染者数量. 文献[3]研究了意识对传染病爆发的影响，并在模型中加入了两个时滞:一个是有意识人群记忆衰退的时滞，另一个是从疾病发生到意识行为发生改变之间的时滞. 研究表明，媒体报道对疾病防控具有重要的作用. 文献[4]研究了媒体报道对具有媒介传播的传染病的影响，建立了一个非线性传染病模型. 通过分析发现，在人群中意识的存在使得疾病的侵袭变得很困难，并且通过媒体的持续报道和意识的迅速传播，可以彻底根除这种疾病. 文献[5-6]考虑到了某些疾病具有较长的潜伏期，建立了具有媒体报道和潜伏期的传染病模型. 结果表明，媒体报道可以有效减少感染者的数量，遏制疾病传播. 文献[7-11]考虑到了在媒体报道作用下接种疫苗的情况，建立了具有媒体报道和疫苗接种共同影响的传染病模型. 通过研究发现，媒体报道和疫苗接种能够有效的减轻疾病的扩散，减少传染病的危害. 文献[12]建立了受媒体报道和疫苗接种共同影响的传染病模型. 研究发现，如果接种疫苗的人对传染病的防范过于自信，那么媒体报道对疾病的传播可能会产生不良影响. 文献[13]建立了受媒体报道影响的传染病模型，将易感者分为了有意识的易感者和无意识的易感者，并且考虑到了信息从被人们接受到发生行为改变这个过程中时滞的影响. 通过分析发现，在媒体报道的影响下，人们意识不断提高，有效的减轻了传染病的传播.

考虑到只有有意识的易感者才会接种疫苗，而无意识的易感者不会接种疫苗，并且有意识的易感者的感染率应该低于无意识的易感者的感染率. 因此，本文在文献[12]和文献[13]的基础上建立了一个受媒体报道和疫苗接种共同影响的传染病模型，分析了媒体报道和疫苗接种对传染病的重要影响.

1 模型的建立

模型分为无意识的易感者Sn(t)，有意识的易感者Sa(t)，感染者I(t)，接种者V(t)和媒体报道信息量M(t)五个仓室.设总人口为N(t)，则N(t)=Sn(t)+Sa(t)+I(t)+V(t).设A为人口的输入率，d为自然死亡率，a为感染疾病的死亡率，β0和β1分别为染病者对无意识的易感者的传染率和对有意识的易感者的传染率，并且β0>β1.λ为从无意识的易感者变成有意识的易感者的转化率，λ0为有意识的易感者的意识丧失率，θ为有意识的易感者的疫苗接种率，r为染病者经过治疗后的康复率，μ为媒体项目贯彻率，μ0为媒体宣传过程中信息耗散率，ω为接种疫苗后的免疫丧失率，p和q分别表示感染者经过治疗后恢复到无意识的易感者和有意识的易感者的比例，并且p+q=1，f和δ分别表示接种者免疫丧失后，从接种者变成无意识的易感者和有意识易感者的比例，并且f+δ=1.依据以上假设，建立如下模型：

(1)

系统(1)的初始条件为

Sn(0)≥0,Sa(0)≥0,I(0)>0,V(0)≥0,M(0)>0.

(2)

假设所有的参数都是正常数.

下面研究系统(1)在条件(2)下解的非负性和有界性，记

由下面的定理可知Γ为系统(1)的正向不变集.

定理1 系统(1)在条件(2)下的解(Sn(t),Sa(t),I(t),V(t),M(t))始终是非负有界的.

证明：首先证明解的非负性. 将系统(1)表示成向量形式，令

Y=(Sn,Sa,I,V,)T∈R5，

(3)

其中F∶R5→R5且F∈C∞(R5)，则上式变为

(4)

下面证明解的有界性. 总人口N(t)满足下面的微分方程

从而集合Γ为系统(1)的正向不变集. 定理得证.

2 基本再生数和平衡点稳定性分析

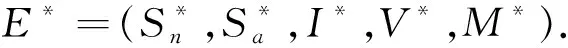
(5)

(6)

求得

(7)

其中：

X1=(ω+d)[λμ(r+d+a)+rqμ0β0]>0,

X2=β1(ω+d)(λμ+μ0β0)>0,

X3=μ0β0[(λ0+d+θ)(ω+d)-ωδθ]>0.

将系统(6)前四个式子相加得

由此得到关于I*的方程为

a1I*2+a2I*+a3=0,

(8)

其中：

a1=(d+a)X2,

显然a1>0.而当R0>1时，有a3<0，此时式(8)存在唯一的正根：

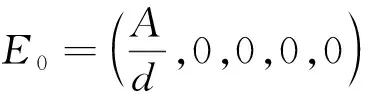
证明:系统(1)在无病平衡点E0处的雅可比矩阵为

则矩阵JE0的特征方程为

(9)

其中：c1=λ0+θ+ω+2d>0,c2=(λ0+d+fθ)ω+d(λ0+θ+d)>0， 显然，式(9)有Z1=-d<0，Z2=-μ0<0两个根.令

g(Z)=Z2+c1Z+c2,

显然方程g(Z)=0的两个根都具有负实部.又因为Z3=(R0-1)(r+d+a)，则当R0<1时，有Z3<0，无病平衡点E0是局部渐近稳定的；当R0>1时，有Z3>0，无病平衡点E0是不稳定的.定理得证.

定理4 当R0<1时，系统(1)的无病平衡点E0在Γ内是全局渐近稳定的.

证明：构造Lyapunov函数L=I，L沿系统(1)轨线的全导数为

β0I(Sn+Sa)-(r+d+a)I≤

(R0-1)(r+d+a)I.

(10)

(Z+d)(Z2+b1Z+b2)=0.

定理5 假设q=0，则当R0>1，且如下条件(11)成立时

(11)

最后，质量管理不到位。质量是工程施工进度的主要影响因素之一，结合我国建筑工程实践来看，在建筑工程施工中，针对施工人员工作行为以及技术操作的管理未得到有效的落实，不规范操作的现象十分常见，这为工程施工质量埋下了严重的隐患，不可避免的波及到了施工进度。

令

Hk=(-1)kDk，k=1,2,3,4,5.

Dk为矩阵JE*的k阶顺序主子式.计算得

H1=λM*+β0I*+d,

H2=(λM*+β0I*+d)(λ0+β1I*+θ+d)-

λ0λM*,

a)+β0I*rqθ+(β0-β1)I*rqd,

θβ0I*].

3 疾病的持久性

定理6 当R0>1时，存在ε>0，使得具有初值条件

Sn≥(0),Sa≥(0),I(0)>0,V(0)≥(0),M(0)≥(0)

的解(Sn(t),Sa(t),I(t),V(t),M(t))满足

证明:设

X={(Sn,Sa,I,V,M)|Sn≥0,Sa≥0,I≥0,V≥0,M≥0},

X0={(Sn,Sa,I,V,M)∈X|Sn≥0,Sa≥0,I>0,V≥0,M≥0},

∂X0=XX0.

易证X和X0是正不变的，∂X0为X中的闭集，系统(1)是点耗散的.定义M∂为

M∂={(Sn(0),Sa(0),I(0),V(0),M(0))|Sn(t),Sa(t),I(t),V(t),M(t)∈∂X0,∀t≥0}.

先证

M∂={(Sn,Sa,0,V,M|Sn≥0,Sa≥0,V≥0,M≥0}.

所以

M∂={(Sn,Sa,0,V,M|Sn≥0,Sa≥0,V≥0,M≥0}.

记

Ω=U{ω(Sn(0),Sa(0),I(0),V(0),M(0))|Sn(0),Sa(0),I(0),V(0),M(0)∈M∂},

其中ω(Sn(0),Sa(0),I(0),V(0),M(0))表示从点(Sn(0),Sa(0),I(0),V(0),M(0))出发的解的ω-极限集.在M∂上系统(1)变为

因此当t→∞时，M(t)→0，所以考虑以下极限系统：

(12)

(13)

则定理得证. 由文献[15]知，欲使式(13)成立，只需要证明下式成立

Ws(E0)∩X0=Ø

(14)

这里Ws表示E0的稳定流形.使用反证法，假设Ws(E0)∩X0≠Ø，则存在

(Sn(t),Sa(t),I(t),V(t),M(t))∈X0,

当t≥0，t→∞时有

(15)

(16)

由式(15)知，存在t1>0，使得当t>t1时，有

则由系统(1)得

由式(16)得，当t→∞时，有I(t)→∞，这与式(15)矛盾，所以式(14)成立.定理得证.

4 数值模拟

为了分析媒体报道和疫苗接种在系统(1)中的作用，本节分别利用意识转化率参数λ和疫苗接种率参数θ对系统(1)进行了数值模拟.

首先，考虑如下参数值：

A=2,λ=0.9,β0=0.06,λ0=0.05,r=0.08,p=1,q=0,ω=0.15,f=0.8,d=1/78,β1=0.03,θ=0.9,δ=0.2,a=0.001,μ=0.3,μ0=0.1.

(17)

取初值(5,50,4,6,7)，此时R0=99.765>1，正平衡点E*存在，由图1可知，正平衡点E*=(0.041,3.454,126.233 6,16.833 8,378.700 8)是全局渐近稳定的.

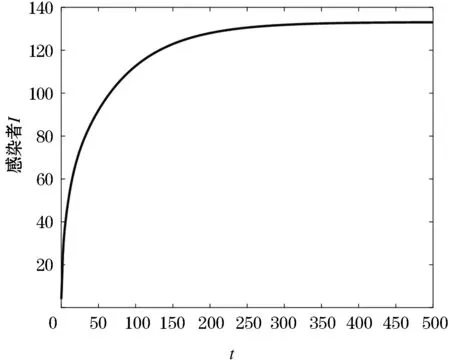
图1 正平衡点E*=(0.041, 3.045 4, 126.233 6, 16.833 8, 378.7008)全局渐近稳定.Figure 1 Positive equilibrium E*=(0.041, 3.045 4, 126.233 6, 16.833 8, 378.7008) is globally asymptotically stable

再考虑如下参数值

A=1,λ=0.9,β0=0.006,λ0=0.05,r=0.8,p=1,q=0,ω=0.15,f=0.8,d=1/78,β1=0.003,θ=0.9,δ=0.2,a=0.01,μ=0.3,μ0=0.1.

(18)

在式(18)这组参数下，取初值(5,50,4,6,7)，此时R0=0.568 8<1由图2可知，无病平衡点是全局渐近稳定的.

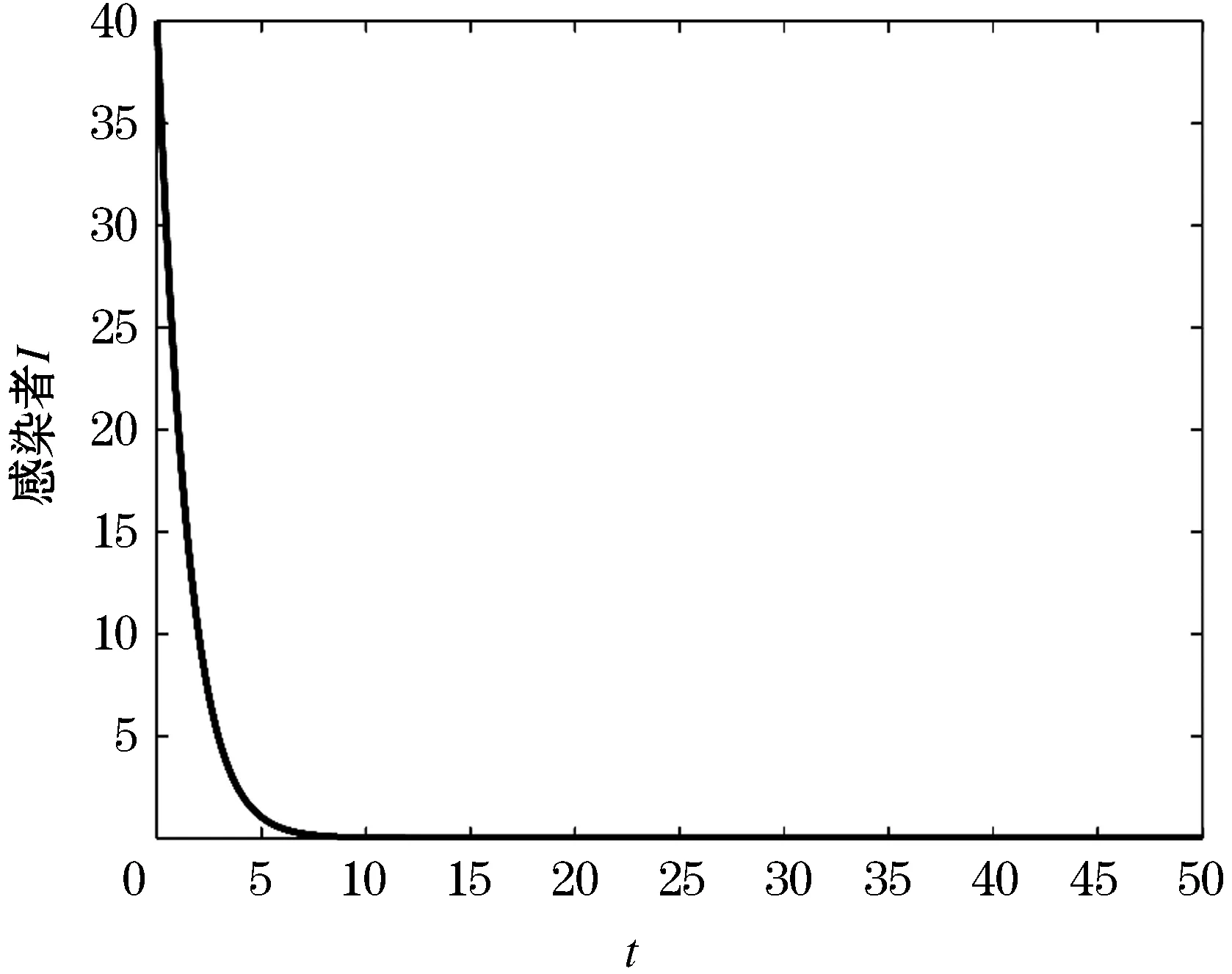
图2 无病平衡点E0=(78,0,0,0,0)全局渐近稳定Figure 2 The disease-free equilibrium E0=(78,0,0,0,0)is globally asymptotically stable

在式(17)这组参数下，考虑意识转化率λ和疫苗接种率θ对系统(1)的影响，得到图3.首先，对意识转化率λ进行不同取值，得到了图3(A). 然后对疫苗接种率θ进行不同取值，得到了图3(B).

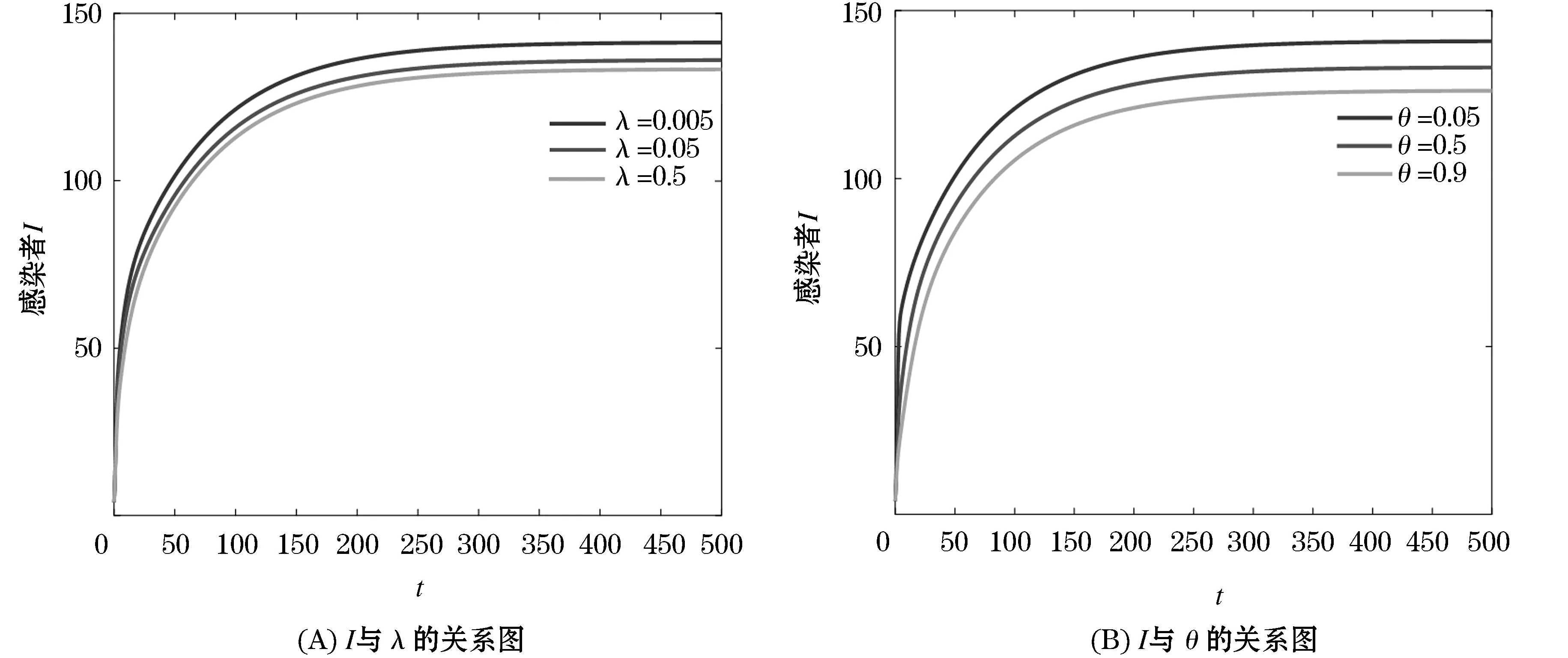
图3 I关于λ和θ的关系图Figure 3 A diagram of Ι with λ and θ

由图3可以看出，当意识转化率增加或者疫苗接种率增加时，都可以有效减少感染者的数量. 因此，当人群中出现感染者时，通过媒体的持续报道，增强人们对疾病的防范意识以及提高疫苗的接种率，都非常有利于遏制传染病的进一步扩散，有利于及时对疾病进行有效防控.

5 结 语

本文建立了一个受媒体报道和疫苗接种共同影响的传染病模型，假设只有有意识的人群才会接种疫苗，并且染病者对两类易感者的传染率是不同的.首先，证明了系统(1)解的非负性以及有界性，然后计算得到了模型的基本再生数R0，给出了平衡点存在的条件.系统(1)永远存在一个无病平衡点E0，并且在一定条件下，还存在一个地方病平衡点E*.分析表明当R0<1时，无病平衡点E0是全局渐近稳定的；当R0>1时，无病平衡点E0是不稳定的.在某些条件下，地方病平衡点E*是局部渐近稳定的，并证明了疾病的持久性.通过数值模拟对理论结果进行了验证，研究发现当意识转化率或疫苗接种率增加时，可以有效减少感染者的数量.因此，当人群中出现感染者时，通过媒体的持续报道，提高人群对疾病的防范意识以及提高人群的疫苗接种率都非常有利于疾病的防控.