基于变邻域的改进AGV路径规划算法
2023-01-08陈远浩吴明晖洪孔林
陈远浩,吴明晖,李 阳,洪孔林
(上海工程技术大学机械与汽车工程学院,上海 201620)
0 引言
在移动机器人领域中,自动引导车(Automated Guided Vehicle,AGV)广泛应用于工业场景的物料搬运工作[1]。路径规划是指移动机器人通过即时定位与地图构建(Simultaneous Localization and Mapping,SLAM)获得环境地图信息后,通过路径规划算法获得最优路径,决定AGV 在工厂环境中的工作效率[2]
目前,国内外主流路径规划算法包括遗传算法(Genetic Algorithm,GA)[3]、快速随机搜索树(Rapidly-exploring Random Tree,RRT)[4]、A*算法[5]等。
(1)GA 为全局智能优化搜索算法。Elhoseny 等[6]提出一种在动态环境下基于贝塞尔曲线的改进GA 路径规划算法,提高生成解的多样性。在染色体多样性度量值低于阈值时,才在每次迭代中接受染色体多样性,从而帮助GA 跳出局部最优解。但由于工厂环境复杂,GA 算法会随着种群增加,运算速度降低,最终还是会陷入局部最优解。
(2)RRT 属于采样搜索算法。Wang 等[7]提出一种基于强化学习的多RRT 方法,用于规划窄道机器人路径,将树的选择过程抽象为多臂赌博机问题,使用优化的强化学习算法进行选择。该算法运算速度快、搜索能力强,但在工厂环境下搜索时盲目性大、在高维度环境下耗时长、易陷入局部最优。
(3)A*算法属于启发式搜索算法。现已经在无人机[8]、智能工厂[9]、智慧农业[10]等领域广泛应用。Bing等[11]通过后阶段局部路径平滑算法提高A*算法的规划成功率。Xin 等[12]基于无限邻域思想优化传统A*算法的搜索方向,但降低了运算速度。陈伟华等[13]提出一种基于双重A*算法的移动机器人路径规划方法,使机器人在动态环境中也能实现安全导航,提高了路径规划效率。
虽然A*算法已广泛应用于工厂AGV 作业场景,但仍存在以下不足:①当SLAM 建立的环境地图较大时,传统A*算法会计算许多冗余节点,计算时间显著增长;②厂区规划AGV 安全行驶区域,相较于其它环境地图更规律,但A*算法的评价函数尚未对此进行优化;③A*算法的路径冗余节点较多,所规划的路径平滑度较差。
针对上述问题,本文提出一种基于变邻域的改进A*路径规划算法。首先,将传统3×3 邻域搜索方式改进为7×7 邻域搜索;然后,基于终点向量的变邻域搜索方法动态优化搜索邻域范围;接下来,融合预先建立的地图信息优化代价函数;最后,通过插点法优化冗余节点。
1 改进A*路径规划算法
1.1 传统A*算法
Hart[14]提出的A*路径规划算法在Dijkstra[15]算法的基础上增加启发式函数,在保证最优性的同时,增加目标节点信息以提升搜索效率。算法具体步骤如下:
步骤1:初始化栅格地图及起点终点信息。
步骤2:初始化close 及open两个空列表。
步骤3:将起点坐标设置为当前坐标并存入open。
步骤4:判断当前节点是否为终点,若是则输出路径结束算法,反之执行步骤5。
步骤5:搜索当前可扩展的所有子节点。
步骤6:计算子节点代价值F(n)并将子节点信息存入open。
步骤7:判断是否遍历所有可扩展节点,若遍历完执行步骤8,反之执行步骤5。
步骤8:计算F(n)最小子节点并从open 中删除该节点,之后存入close。
步骤9:设置该节点为当前节点,并执行步骤4。
算法的代价值表达式为:

式中,n代表各个节点,F(n)代表当前节点n的总体代价值,G(n)代表AGV 的起点坐标到当前节点n所在坐标的代价值,H(n)代表AGV 当前节点n所在节点的坐标到终点坐标的代价值。
常见的H(n)计算方法包括曼哈顿距离、欧几里得距离、对角线距离等[16]。本文选择欧几里得距离作为H(n)的代价函数,数学表达式如式(2)所示:
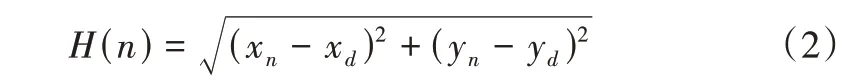
式中,(xn,yn)为当前节点所在坐标,(xd,yd)为终点所在坐标。
1.2 多邻域拓展及变邻域搜索方法
如图1(a)所示,传统A*算法采用3×3 邻域搜索方式,当转角过大时,会对AGV 的运动会造成影响,因此设置当前节点到子节点的转角均为45°的整数倍。
当面对大且复杂的环境地图时,该方式会计算冗余搜索节点,浪费计算资源。为此,通过多领域拓展搜索方法将当前节点到子节点的转角从45°的整数倍优化为多角度。同时,采用7×7 邻域搜索方法减少冗余节点的计算,如图1(b)所示。此外,将原有8 个子节点增加到48 个子节点,并将AGV 的移动方向从8个优化到32个。
在AGV 实用场景中,由于受安全区域限制,AGV 所处环境较为简单,不容易陷入“死胡同”,死锁发生可能性较低。因此,大量与终点方向相反的子节点往往是冗余搜索节点。针对该问题,本文基于终点向量的变邻域搜索方法,根据节点到终点的向量,将48 邻域搜索优化至27 邻域搜索,如图1(c)所示。
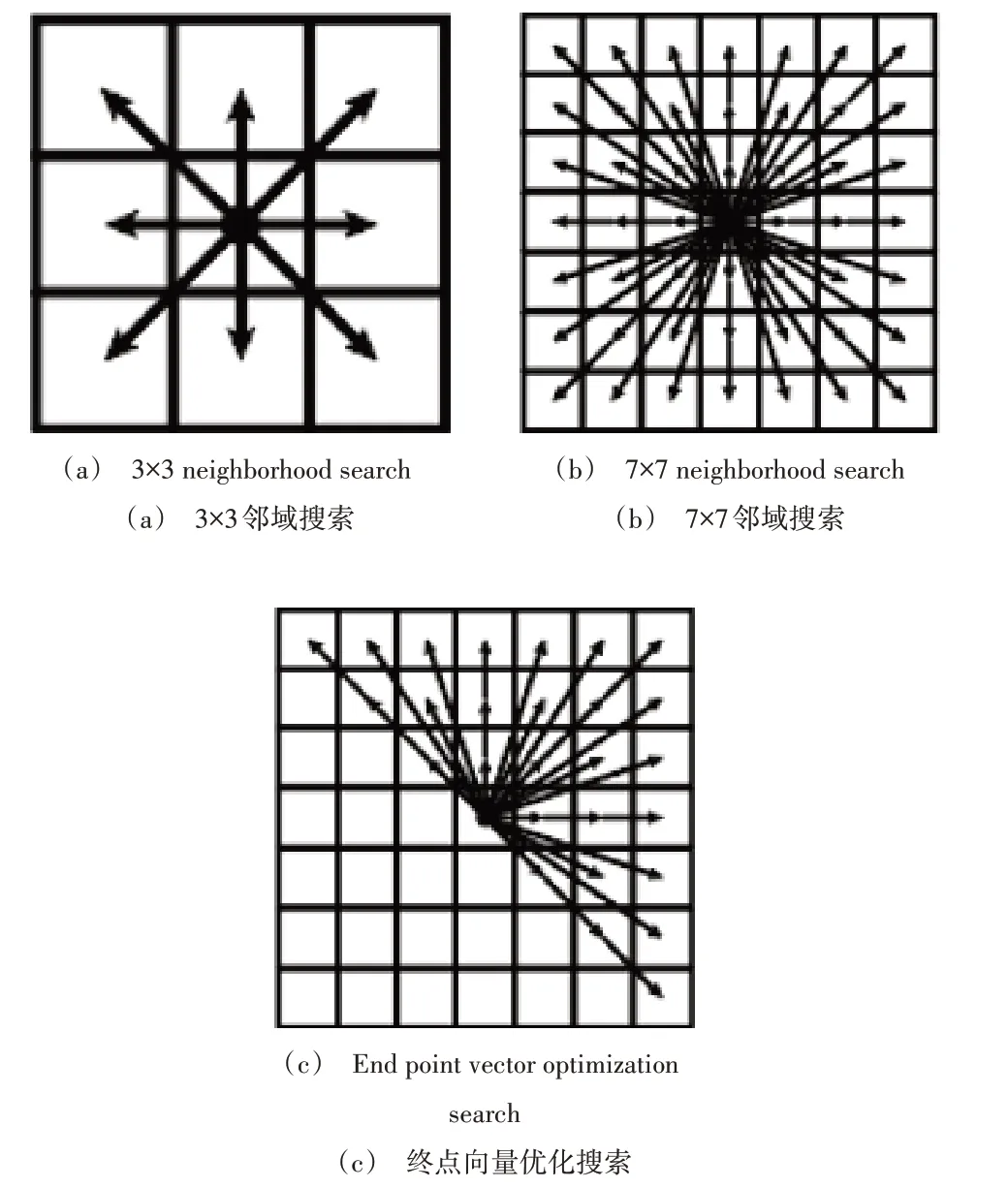
Fig.1 A*algorithm neighborhood search methods图1 A*算法邻域搜索方式
设(xn,yn)为当前节点所在的坐标,(xd,yd)为终点所在坐标,则终点向量可定义为:
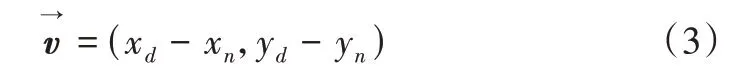
设θ为终点向量与x轴正向方向的夹角,则根据终点向量优化的搜索邻域如表1、图2所示。

Table 1 Endpoint vector optimization neighborhood表1 终点向量优化邻域
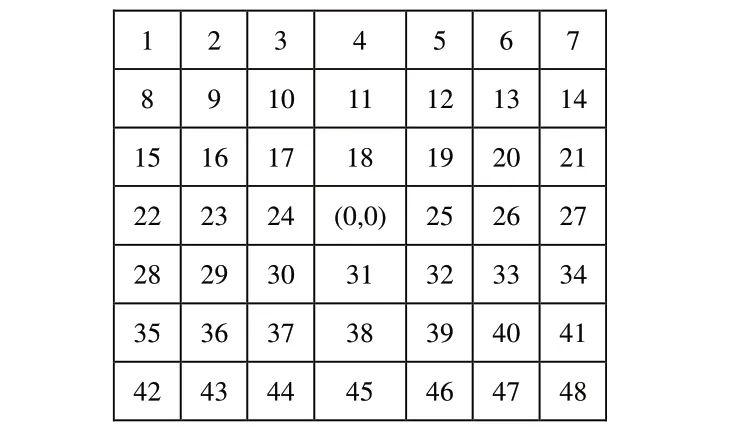
Fig.2 Neighborhood coordinate number图2 邻域坐标编号
1.3 代价函数优化
传统A*算法的启发函数在代价函数中会影响A*算法的效率。当H(n)<G(n)时,搜索节点多、效率低,路径短;当H(n)>G(n)时,搜索节点少、效率高,但无法保证规划的是最优路径。综上所述,当环境地图较为规则且搜索节点接近终点时,需要较大的启发函数;当地图环境较复杂且算法搜索节点较多时,则需要较小的启发函数[17]。为此,融合当前节点及环境地图信息,将代价函数改进为:

式中,d为当前节点到终点的距离,D为起点到终点的距离,N为可行区域占栅格地图的比重。
1.4 插点法优化
插点法又称Floyd 算法,利用动态规划思想寻求两点之间最短路径[18]。如图3 所示,为进一步优化A*算法规划的冗余节点,在AB之间插入D点。其中,A、B、C为初次规划的路径,dist(A,C)为A到C的最短距离。
由于A、C间存在障碍物无法直接形成路径,因此dist(A,C) 为+∞。通过计算可得dist(A,C) >dist(A,D) +dist(D,C),并且满足dist(A,B) +dist(B,C) >dist(A,D) +dist(D,C),因此ADC为最优路径。

Fig.3 Redundant path optimized by Floyd algorithm图3 插点法优化的冗余路径
1.5 改进A*算法流程
基于变邻域的改进A*算法流程如下:
步骤1:初始化栅格地图及起点终点信息。
步骤2:初始化close 及open两个空列表。
步骤3:将起点坐标设置为当前坐标并存入open。
步骤4:判断当前节点是否为终点,若是则插点法优化冗余路径、输出路径结束算法,反之执行步骤5。
步骤5:搜索当前基于终点向量优化的7×7 邻域子节点。
步骤6:计算子节点代价值F(n)并将信息存入open。
步骤7:判断是否遍历所有可扩展节点,若遍历完则执行步骤8,反之执行步骤5。
步骤8:计算F(n)最小的子节点,并将其从open 中删除,然后存入close。
步骤9:设置该子节点为当前节点,并执行步骤4。
2 实验结果及分析
2.1 实验设计
本文使用MATLAB 建立3 个30×30 的AGV 工厂仿真栅格地图A、B、C,起点坐标均为(1.5,1.5),终点坐标均为(30.5,30.5),如图4 所示。在3 组不同地图中分别使用GA算法、RRT 算法、传统A*算法和改进A*算法进行AGV 路径规划。并且,分别比较4 种算法的路径长度、搜索节点个数、运行时间、累积转角度数等性能指标。
2.2 结果分析
图5 为地图A 的实验效果,3 组实验的具体数据见表2。
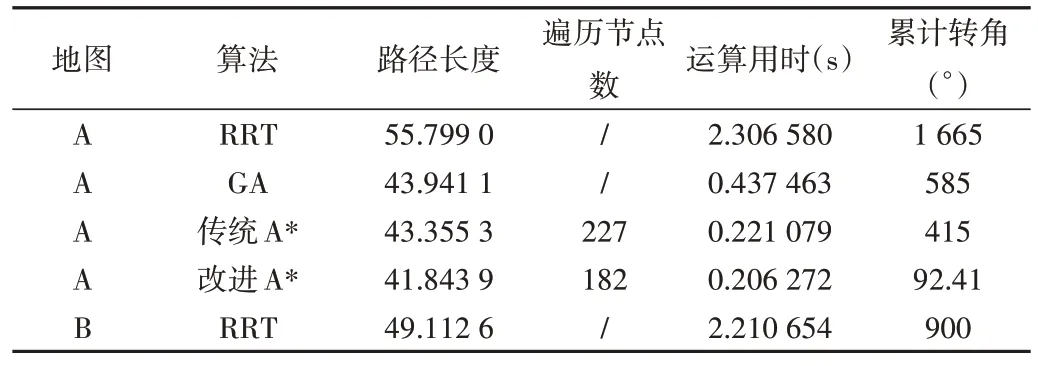
Table 2 Experimental data表2 实验数据

续表
通过比较每组实验数据可得出以下结论:
(1)RRT 算法由于基于随机采样搜索,导致其搜索时间不稳定,且输出的路径随机相较于传统A*算法及改进A*算法更长。
(2)在栅格地图环境中,RRT 算法及遗传算法的复杂度较高,计算时间相较于A*算法及改进A*算法更长。
(3)改进A*算法相较于传统A*算法,所规划路径长度更短,显著提高了AGV 的作业效率。
(4)改进A*算法遍历节点数更少,算法运算时间更短,算法性能存在一定提升。
(5)改进A*算法累计转角度数更小,AGV 能够规划更合理的路径,以减少不必要的转向。

Fig.4 Simulation grid map of three different AGV plants图4 3种不同AGV工厂仿真栅格地图
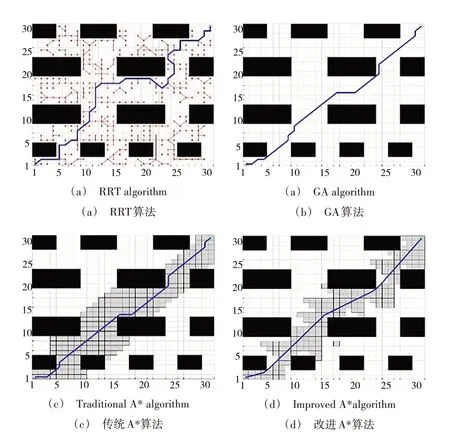
Fig.5 Experimental results of different algorithms on map A图5 不同算法在地图A的实验效果
2.3 实验验证
将改进A*算法应用于激光雷达AGV 中,AGV 实物主体如图6(a)所示,图6(b)为AGV 导航过程。

Fig.6 Application of A*algorithm on lidar AGV图6 A*算法应用于激光雷达AGV
此外,利用改进A*算法在SLAM 算法建立的工厂环境地图中,规划初始点到终点的最优路径。为了减少实际误差和实验偶然性,分别通过不同算法进行3 组由多个导航点组合而成的任务。由图7 可知,改进A*算法相较于其它算法,有效减少了规划路径的长度及累计转角。
3 结语
本文针对AGV 作业的环境特点,设计一种基于变邻域的改进A*路径规划算法。该算法首先扩展传统A*算法的搜索邻域;然后引入终点向量优化冗余搜索邻域,基于环境信息及当前节点信息优化代价函数;最后通过插点法优化冗余节点,提高路径平滑度。

Fig.7 Experimental results of different algorithms图7 不同算法实验结果
仿真实验及实物验证表明,该算法在AGV 工厂环境下,路径长度、遍历节点数、运算用时、累计转角等方面均优于传统A*算法,工作效率及AGV 运动平滑度得到了显著提升。
