云制造生产模式下的生产调度研究

万雨松，余开朝

（昆明理工大学机电工程学院，云南昆明 650093）

0 引言

我国各地区制造业水平差别巨大，制造资源分布极不均匀，并且存在着制造企业拥有很多制造资源，但由于没有充足的制造任务致使其被闲置的现象，从而导致了制造资源的浪费［1］。针对该情况，并且考虑到《中国制造2025》战略目标的需要，李伯虎院士［2］提出了云制造这一全新的生产模式。

云制造是源于工业4.0 概念的一种新的制造模式，其可采用网络技术充分利用分散的生产资源。在云制造过程中，集中利用分散的制造资源合理安排各级生产计划，为需要的客户提供制造服务［3］。然而，云制造这种新型生产模式给生产调度提出了新问题：从整体生产的角度而言，需要实时和快速反应的调度方法可大大提升分散制造资源的利用率，但相应地在生成生产调度计划时会存在效率问题。

目前学者们对于云制造的研究主要是考虑制造的服务属性，如Vahedi 等［4］在参与云制造的工厂之间建立相关权重，并设置提交订单客户的偏好权重，以便更好地进行任务匹配；郭亮等［5］研究云制造不同任务层次的加工任务匹配，构建了相对应的优化任务匹配模型。但目前已有研究比较关心的是云制造的服务属性，对于云制造模式下的生产相关部分的研究较少。

云制造调度问题面向的是多样化的产品需要和众多的柔性制造资源，因此如何更好地解决柔性作业车间调度问题（Flexible Job Shop Scheduling Problem，FJSP）是解决云制造调度问题的基础［6］。FJSP 是在最典型的车间调度问题（Job Shop Scheduling Problem，JSP）和可选择加工机器的基础上扩展产生的问题［7］。对于一个制造资源中心，加工工件的多个工序都可在制造资源中心进行加工，并且每一个工序都有一个或多个机器选择，这就是柔性车间调度问题。

目前对FJSP 的研究主要是如何求得高质量和更优的解。如Yazdani 等［8］提出一种混合整数线性规划模型，并且结合进化算法最小化FJSP 的完工时间；Brucker 等［9］证明了FSSP 是一个NP-hard 问题，即问题可能的解会随着问题规模的扩大而以爆炸般的速度增加。因此，精确方法在解决大规模柔性调度问题时效率不高，因其计算量很大。例如混合整数线性规划的求解方式可构造数学模型并求取全部解，但相对应的是求解时间很长，所以很难处理和求解云制造模式下的大规模调度问题。

因此，元启发式方法逐渐成为FJSP 最主要的研究方向。各种元启发式方法如粒子群算法、遗传算法、退火算法等被用于解决FJSP 问题。例如，Pezzella 等［10］使用优化的遗传算法（Genetic Algorithm，GA）求解FJSP 问题，该算法使用不同策略生成初始种群、选择个体并进行迭代搜索；代招等［11］在初始种群中利用混沌映射和反向学习策略提高初始种群质量，进而提高算法收敛速度；Huang 等［12］在交叉方法和变异方法基础上对遗传算法进行改进，在子代种群生成过程中采用新的自适应交叉和变异概率，大大提高了收敛速度；顾幸生等［13］使用博弈解集，在粒子群算法基础上对种群迭代进行改进，将改进算法用于求解FJSP。

然而，常用于求解FJSSP 的元启发式算法本身存在一定缺点，比如遗传算法的编码可能会出现不可行解的问题，需要增加剔除不可行解的步骤，导致计算量增加，并且因采用基于概率搜索的方式，所以在局部搜索时效率较低。粒子群算法在求解FJSP 离散组合问题时性能不佳，容易快速损失种群多样性，迭代至局部最优的陷阱中。因此，将不同算法结合，充分发挥各自算法的优点也是常用的算法优化手段。Li 等［14］将具有良好全局搜索能力的遗传算法与具有良好局部搜索能力的退火算法相结合，提出一种新的混合算法；Rohaninejad 等［15］针对FJSP，开发了一种将GA、粒子群算法（Particle Swarm Optimization，PSO）与局部搜索启发式方法相结合的新型混合算法；Zhang 等［16］处理FJSP 时将可变邻域搜索引入到GA 算法中，提升了求解质量，但是相应的算法运行时间大幅增加。

云制造的概念有一部分源自于云计算，在研究过程中，很多学者主要研究制造架构，针对制造生产部分的研究较少。因此，本文主要研究云制造模式在制造层面的生产情况，对云制造环境下的FJSP 问题需要考虑求解速度和质量的问题，进一步优化求解的元启发式算法，以优化云制造环境下的生产能力。为了在保证算法搜索性能的基础上加快求解速度，本文基于候鸟算法，利用分享邻域解的机制提升寻优速度；使用矩阵编码方式，省去了染色体修复步骤；采用3 种种群初始化策略，以保证种群质量和解空间分布，有助于快速搜索到最优解附近；引入变邻域搜索，但是只有优秀个体才会进行此搜索，在保证搜索能力的同时，可减少算法运算时间。

1 问题模型

1.1 云制造模式与调度框架

如图1 所示，在云调度生产模式中，个人或企业用户根据自身需要提交制造需求订单，生产订单会在云制造平台上拆分成不同的加工部件生产任务，然后这些任务会根据企业的制造能力进行匹配调度。生产任务的分配结果会返送给客户和企业，企业再将生产任务拆分成工序，进行柔性生产调度，并将调度结果下达至生产一线进行生产。

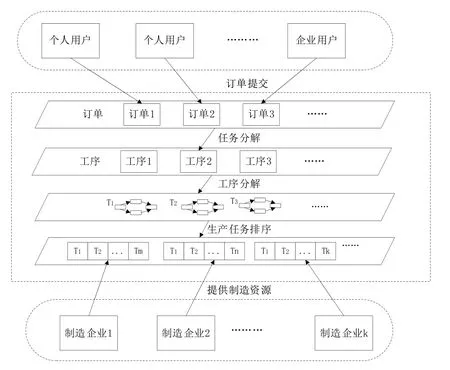
Fig.1 Cloud manufacturing production mode图1 云制造生产模式

针对云制造模式下的生产任务排序与机器选择的组合问题特性，找到合理的求解方法以充分利用企业的制造能力是有必要的。云制造模式下的柔性调度问题计算适合采用元启发式方法，即在一定时间内获得可接受的调度方案，而不是耗费大量计算时间获得最优解。

根据上文对云制造模式运行的分析，本文提出如图2所示的云制造模式调度框架。第一步是企业对自身已有的生产任务进行调度，并根据调度方案分析设备使用情况，然后将获得的剩余空闲生产能力发送到云制造平台上；第二步是云制造平台对用户提交的制造任务进行分析，将相应的制造任务与空闲制造资源进行匹配，使制造需求方与企业都能满意；第三步是企业接受订单后进行相应的云制造调度，看得到的调度方案是否符合要求，如果可以接受，则调度方案转入生产车间进行执行。

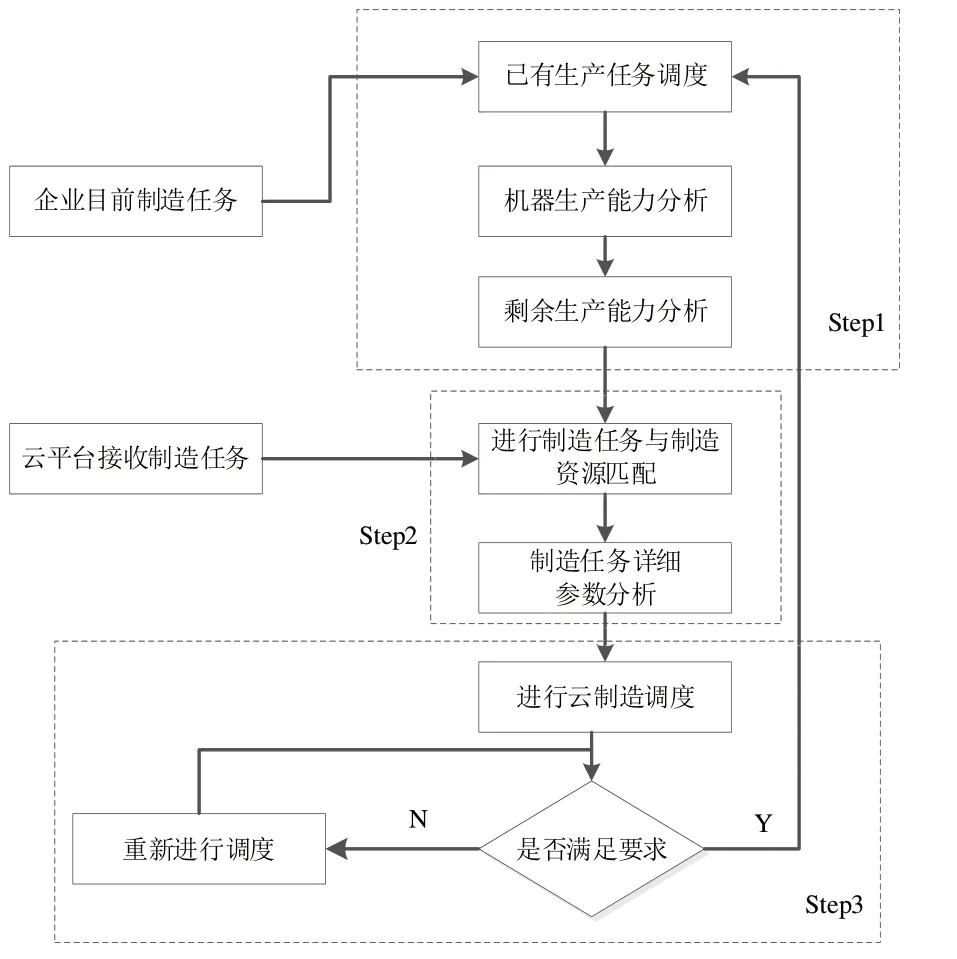
Fig.2 Cloud manufacturing mode scheduling framework图2 云制造模式调度框架

在云制造模式下，生产调度需要考虑的不仅仅是工序的加工顺序排列和工序选择哪个加工设备，而且需要适应整个生产模式的要求。如企业需要制定自身的生产任务计划，然后需要利用空闲的制造资源接收云平台的生产任务，这就要平衡两组任务使用机器时可能导致的加工时间冲突问题。在常规的调度问题基础上，云制造模式下的调度问题还引入了效率要求，所以问题的构成与求解更为复杂。

1.2 云制造模式下FJSP问题模型构建

为更好地描述与解决柔性作业车间调度问题，用以下参数和约束式对FJSP 问题构建相应数学模型，如表1所示。

判断参数：

Table 1 Flexible production scheduling model parameters表1 柔性生产调度模型参数

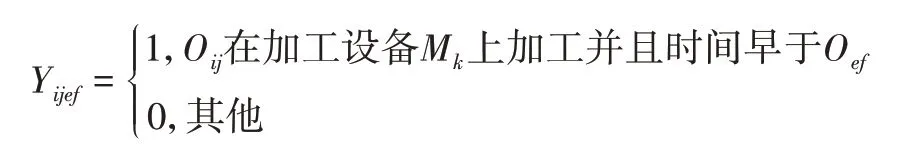
要符合云调度生产模型，就有一定的限制条件，具体如下：

（1）工序约束。

式（1）表示对于每个工件，自身工序的加工顺序是固定的，不可更换。

（2）加工设备约束。

式（2）表示在同一时间，一个加工设备上只能进行一个工序的加工。

（3）加工过程约束。

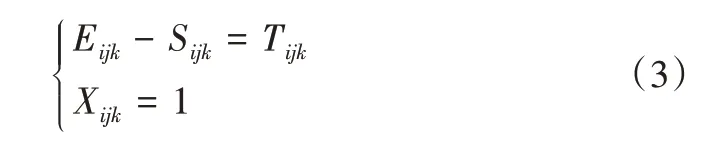
式（3）表示任意加工工序在加工时不能中断。

在上述约束之外，考虑到实际情况，还有一些其他约束：在初始时间，需要加工的工件和对应的加工机器都已准备就绪，所有参数均为非负数。

本文采用的求解指标是最大完工时间最小指标，也是最常用的调度性能指标，具体如式（4）所示。

对一组调度计划来说，就是要求得使时间最长、Ti值最小的调度方案，并且求解方法可扩展成多目标优化求解，也可引入生产平衡率、加工成本等其他生产指标。因此，本文对问题的研究主要基于最大完工时间最小指标，并将本文算法的求解结果与目前国内外比较典型的算法结果进行比较，以衡量算法性能。由于候鸟算法的通用性，尤其是其领飞鸟的设计方案，使得该算法不会受到问题约束条件的影响。

2 候鸟算法

MBO（Migratory Bird Optimization Algorithm）算法是一种利用共享搜索解机制的群体元启发式算法。该方法是基于候鸟在飞行中保持V 型编队以节省能量消耗的原理，由Duman 等［17］在2012 年首次提出，用于解决二次分配优化问题。MBO 算法主要有以下几个步骤：种群初始化、领飞鸟进化更新最优值、跟飞鸟进化更新解、更换领飞鸟，通过这样的循环找到最优解。

初始候鸟群（也即问题可能的解）组成一个V 形编队，包括一个先导候鸟和一些跟随候鸟。如图3 所示，在解决方案群中，为每个候鸟搜索邻域（即在每个解决方案附近生成数量有限的解决方案），评估每个候鸟的相邻解决方案。如果有更好的优化解，则该候鸟将被替换为更好的解决方案。

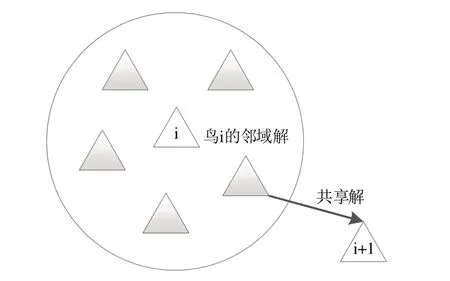
Fig.3 Schematic diagram of excellent neighborhood sharing图3 优秀邻域分享示意图

算法使用分享邻域解来模拟前鸟给予跟随鸟的抬升力，即每个跟随鸟（主要解决方案）都可以在其前鸟共享的解决方案帮助下改进自身解。因此，除领飞鸟外，群体的其他跟飞鸟都有机会被其前面候鸟的邻域加以改进。如图4 所示，算法搜索多次后，领飞鸟由于搜索过久，产生更优解的可能性变小，因此移动到队伍后列，选取后续的跟飞鸟成为新的领飞鸟继续搜索。然后在后续搜索过程中继续同样的替换过程，直到达到迭代次数。最后，引入群体最优解作为MBO 算法的解。

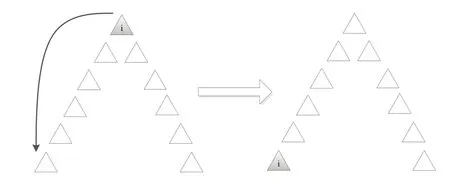
Fig.4 Schematic diagram of replacing the collar bird图4 更换领飞鸟示意图

分析候鸟算法的过程，单个候鸟的不同邻域搜索和进化策略能保证全局分散的搜索能力，共享邻域解能保证单个个体能通过整体的较优解进化，保证算法集中的搜索性能。MBO 算法在局部搜索的能力是比较优异的。

对于启发式算法而言，种群收敛不是越快越好。若种群收敛太快，会在全局搜索不足的情况下过早地聚集在局部解，陷入局部最优。MBO 算法将前面个体的邻域解分享给后面的多个跟随个体，从一方面来看，优化了种群的整体性能，但从另一方面来看，更多候鸟进入到前鸟附近，造成候鸟的种群多样性损失严重，容易陷入局部最优的陷阱。所以需要对MBO 算法进行相应的优化改进，以提升搜索性能。

2.1 编码／解码方案

柔性生产调度会有多种实际生产上的约束，在算法搜索过程中可能会产生不可行解的情况，所以本文使用矩阵编码的方式进行编码：云制造情况下收到n个工件的制造订单，每个工件有m道工序需要加工，每道工序有m（jj=1，2，…，m）台可选择的柔性机器，初始化种群Xn×m的元素Xij采用随机实数生成。式中，i=1，2，…，n，j=1，2，…，m。初始化的候鸟是一个问题的解，对于某个解Xi，整数部分表示待制造元件的柔性机器号，小数部分表示在机器上的加工顺序，优先度按照小数部分降序排列。这种编码方式是将每个矩阵当成一个候鸟，也即一个调度方案。采用该方式不仅能提高计算速度，而且能保证后续搜索、进化不会出现不可行解，节省了计算时间。

解码是对编码的逆向操作，根据得到的矩阵给出合理的柔性调度方案，例如给出一个初始种群X：

就第一列而言，观察整数部分可得：工件J1和J2是在机器一（整数部分）上加工，机器一先加工O11，再加工O21（小数部分升序顺序）；工件J3、J4是在机器二上加工，机器二先加工O31，再加工O4（1小数部分升序顺序）。根据各个工件的加工时间，最后给出一个可行的柔性调度方案。

2.2 种群初始化方案

类似于其他的群体智能算法，良好的种群初始化方法对于丰富种群多样性和提高搜索速度是很有帮助的。生成的初始候鸟种群需要保证质量和多样性，即初始解决方案覆盖的解空间很大，并且接近最优解。为了满足这两个要求，本文用以下3 种方式生成初始解，并且为保证多样性和质量进行了比例划分，具体如下：

（1）随机生成方式。为保证群体的多样性，使用随机生成方法生成60%的初始候鸟，即对于机器选择和操作序列，都是随机生成矩阵序列。

（2）优先机器的选择方法。首先是第一个工序和下一个工序随机选择加工机器，然后记录每台机器的操作时间，在下一个工序Oij选择机器时，将可选择机器之前的加工时间与Oij的加工时间相加，选择总加工时间最短的机器，然后继续下一个工序的机器选择，直到所有工序都选择了对应的加工机器。使用优先机器的选择方法生成20%的初始候鸟，使用该方法的优点是其可在算法初始阶段使机器的工作时间尽量一致，从而更好地探索搜索空间，并考虑机器的工作负载平衡。

（3）优先工件的选择方法。对工件的可选择机器进行随机选择，在机器的加工顺序上，优先加工剩余工序总时长最长工件的一个工序，然后再以同样的规则选择下一个工件进行工序加工。使用优先工件的选择方法生成20%的初始候鸟，该方法的优点是可以搜索到令所有工件加工时间最大值尽可能小的解空间。

2.3 候鸟群进化

在MBO 算法中，领飞鸟是第一个开始搜索邻域解的个体，然后如果有更好的解，则编码矩阵更换为更好的解，这被称为鸟群个体的进化，之后分享自身的优秀解给后续候鸟。这种机制就是模拟实际候鸟队列给后续候鸟的抬升力，后续候鸟可在自身搜索的解和前鸟提供的解中进行选择与进化，这就是候鸟群的进化。搜索解的方法主要是邻域搜索，柔性调度和常规调度的主要区别在于多了机器选择，本文主要采用以下4种邻域搜索策略：

（1）机器随机搜索。任意选择一个工序，将其加工机器改成其他可加工的机器，即整数部分编码改成其他，小数部分随机选择并且保证不重复。

（2）工序交换搜索。随机将一个机器上的两个工序交换（也即交换矩阵编码的小数部分）。

（3）工序前移搜索。随机选取一个机器上的任意两个工序，将后面加工工件的加工顺序插入到另一工件之前，即在插入的两个工件的小数部分之间随机生成一个小数。

（4）工序后移搜索。随机选取一个机器上的任意两个工序，将前面加工工件的加工顺序插入到另一工件之后，即在插入的两个工件的小数部分之间随机生成一个小数。

然而，由于初始的鸟群顺序是随机生成的，一些具有优秀解的候鸟可能处于队伍后方，难以给整个鸟群分享优秀解。因此，根据每个候鸟的适应度函数进行排序，解码后加工时间最短的候鸟排第一，然后依次排序，最差的候鸟在最后，该方式能够分享整个候鸟群的优秀解。同时考虑到MBO 算法的全局搜索能力，在迭代次数达到总搜索次数的一定比例时才开始排序，即设置巡回次数，从而避免种群多样性的快速损失，在后期增强局部搜索能力。局部搜索策略如图5所示。

Fig.5 Local search strategy图5 局部搜索策略

2.4 变邻域搜索

对于元启发式算法，对最优解范围的搜索能力是一个很重要的性能。变邻域搜索算法（VNS）是由Mavrotas等［18］首先提出的用于对给出的算法解进行范围寻优的局部搜索算法，主要原理是通过变动规则在某个较优解附近进行搜索，然后用更好的解替换掉原解。在改进的MBO算法中，变动规则主要是使用2.3 节的邻域搜索策略，对MBO 搜索到的最优解按规则变动进行搜索。主要步骤如下：

步骤1：选取候鸟群进化的最优个体B 作为变邻域搜索的起始值，搜索策略Smax=4，搜索次数Nmax=n。

步骤2：令S=1，从2.3 节的第S 个邻域搜索策略开始对B 的矩阵编码进行搜索变换，得到编码矩阵B1。

步骤3：利用邻域结构设定搜索次数对B1进行搜索，达到搜索次数后将其中的最优解设为B2。

步骤4：若B2是最优解，则将B2赋值给B，跳回步骤2继续搜索；若B 是最优解，则S=2，继续搜索，直到搜索策略S和搜索次数达到上限。

步骤5：选取最优解赋值给B，变邻域搜索结束。

2.5 改进候鸟算法流程

通过上述改进，本文提出了改进候鸟算法（Improved Migratory Bird Optimization Algorithm，IM-MBO），主要流程如下：①按3 种策略进行种群初始化；②领飞鸟通过搜索产生邻域解集U1；③如果产生的邻域解优于领飞鸟，领飞鸟进化为更优解；④跟飞鸟搜索产生邻域解集U2，然后将U1和U2中的最优解与跟飞鸟进行对比，取最优解；⑤选择20%的个体进行变邻域搜索；⑥如果达到巡回次数，进行领飞鸟替换；⑦如果达到终止条件，导出求出的最优解。具体流程如图6所示。

3 实验结果与分析

上述改进候鸟算法用MATLAB 语言实现，编写程序并运行的计算机是Window10 版本，处理器为Intel（R）Core（TM）i5-6300HQ，CPU 主频为2.3GHz，MATLAB 软件型号为MATLAB R2019a。为了测试候鸟算法的性能，选用在柔性调度邻域常用mk 系列的10 个实例［19］，加工工件数目范围为10～20，工序数目范围为5～15，机器数目范围为4～15。元启发式方法每次搜索得出的解可能不一样，为消除运算中的随机性，使最后的结果更具说服力，对每个案例运行10 次计算平均值。对比的目标一方面是遗传（GA）算法和粒子群（PSO）算法这两种常用于调度的元启发式算法，另一方面是Gu 等［20］提出的IGA-AVNS 算法和顾幸生等［13］提出的博弈粒子群算法（Gaming PSO）。参考任彩乐等［21］的研究，算法参数设置鸟群个体为51，候鸟搜索自身邻域解数目k=3，分享给跟随鸟的邻域解数目x=1，巡回次数S=10。求解结果如表2 所示。其中，n 代表需加工的工件数目，m 代表可供选择的机器数目，w 代表总工序数目，S是MBO 算法求解10 次的最优解，Ave 是MBO 算法求解10次获得最优解的平均值，T 是各个算法10 次求解的平均时间。

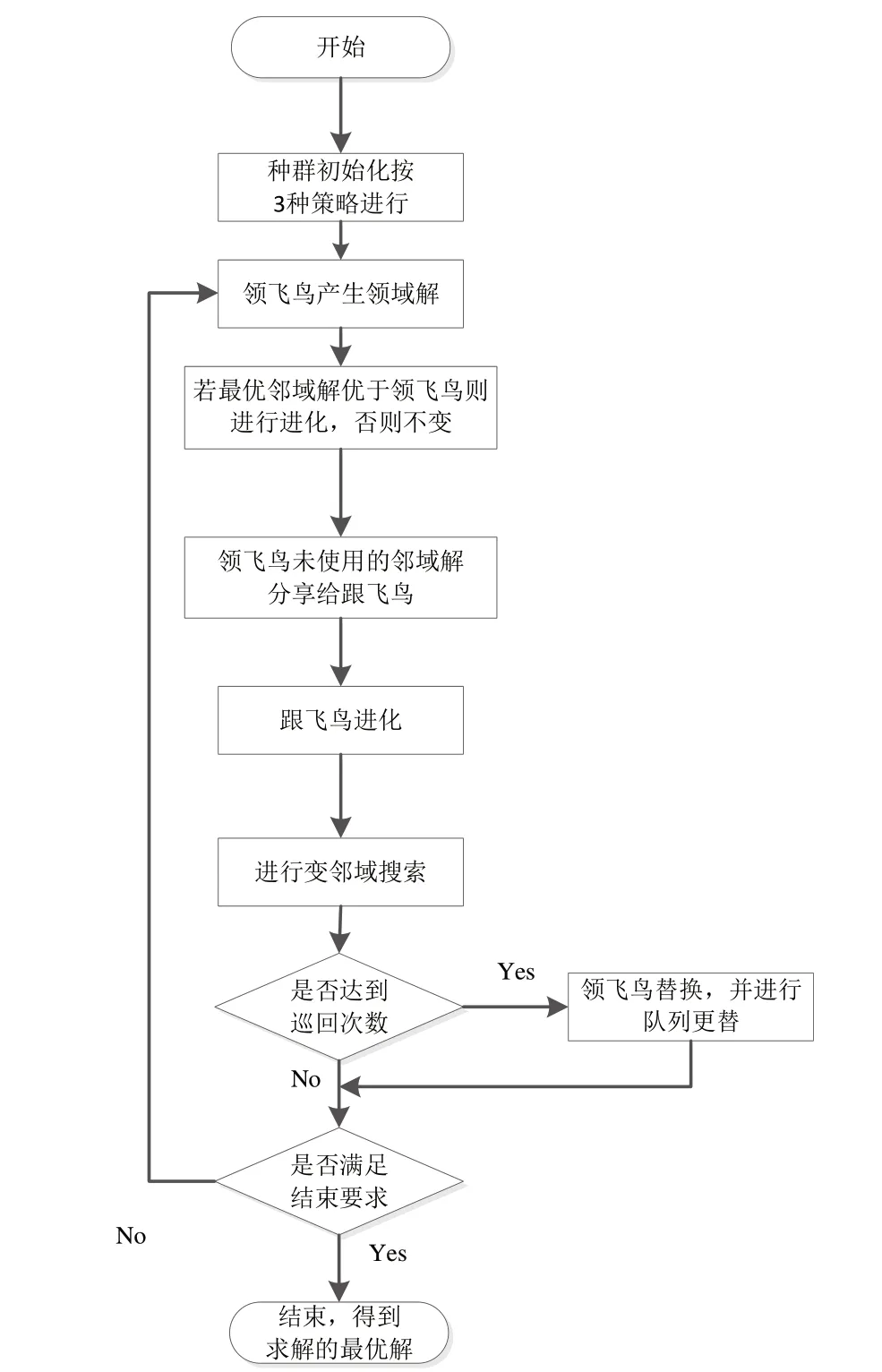
Fig.6 IM-MBO algorithm flow图6 IM-MBO算法流程

对比表2 中数据得出如下结论：先对比在同一运算环境下的3 种算法，对比mk 案例的最优解和平均解，IMMBO 在搜索能力与搜索速度上优于GA 算法和PSO 算法，说明整体的搜索性能良好。在算法运算时间上，由于编码方式不用染色体修复，加快了运算速度，IM-MBO 比GA 算法快34%，比PSO 算法快16%。对另外两位学者的求解结果进行对比，因为运算环境不同，所以不对比运算速度。IM-MBO 在10 个问题上的最优解总体上略优于Gaming PSO 算法，且有部分问题的解优于IGA-AVNS 算法，总体而言在搜索能力上差距不大。考虑到本算法因考虑运算速度，牺牲了部分求解性能，这样的结果是可以接受的。

下面用mk01 的案例进行说明，最终得出调度方案的甘特图如图7 所示（彩图扫OSID 码可见）。数字是加工工件的序号，横轴方向是工序加工时间，纵轴是机器上的加工工序。

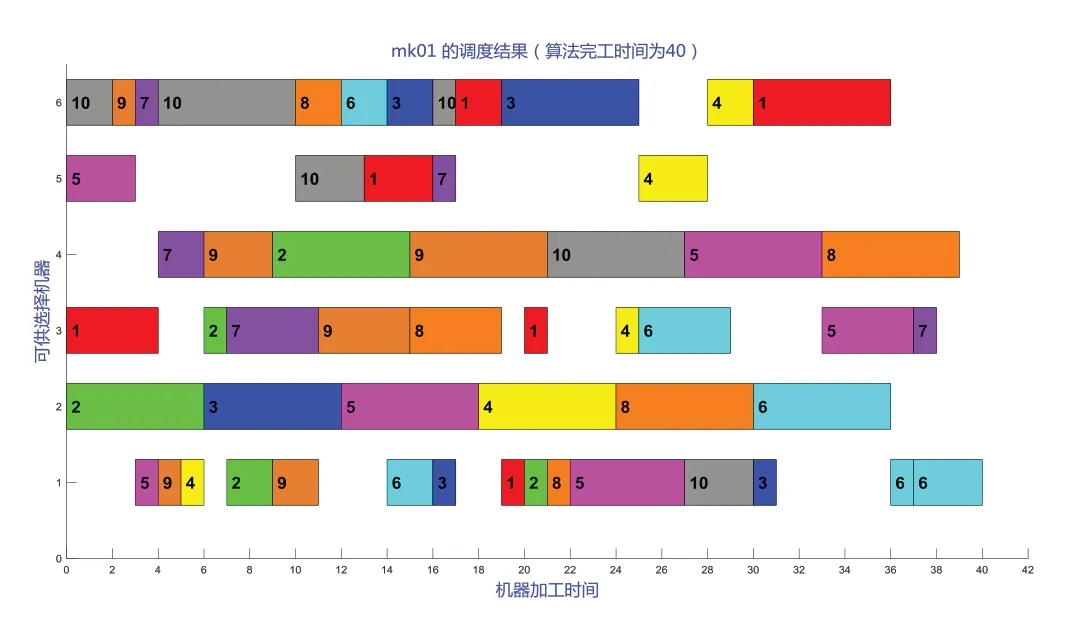
Fig.7 Optimal scheduling result of mk01 of MBO algorithm图7 MBO算法mk01最优调度结果

在计算速度上，PSO 算法由于迭代方式简单，搜索速度比PSO 算法略快，但是代价是易快速损失种群多样性，求解性能降低。为进一步了解MBO 算法的性能，以mk10的基准问题为算例，将本文提出的IM-MBO 与经典的粒子群算法PSO、遗传算法GA 进行收敛性能对比，3 种算法搜索过程如图8 所示。由图8 可知，3 种算法中，IM-MBO 约在60 次迭代时收敛到自身的最优解，最终求解值为215，并且搜索下降速度很快；PSO 初始收敛速度快，但是缺乏全局搜索能力，后期陷入局部最优，求解值为236；GA 收敛速度最慢，但是全局搜索能力尚可，所以初期慢于PSO，但后期不易陷入局部最优，求解值为229，优于PSO。

综上，所得到的IM-MBO 算法在求解速度、收敛速度、全局搜索能力等方面都优于原有算法，可用于云制造模式下的柔性生产调度。

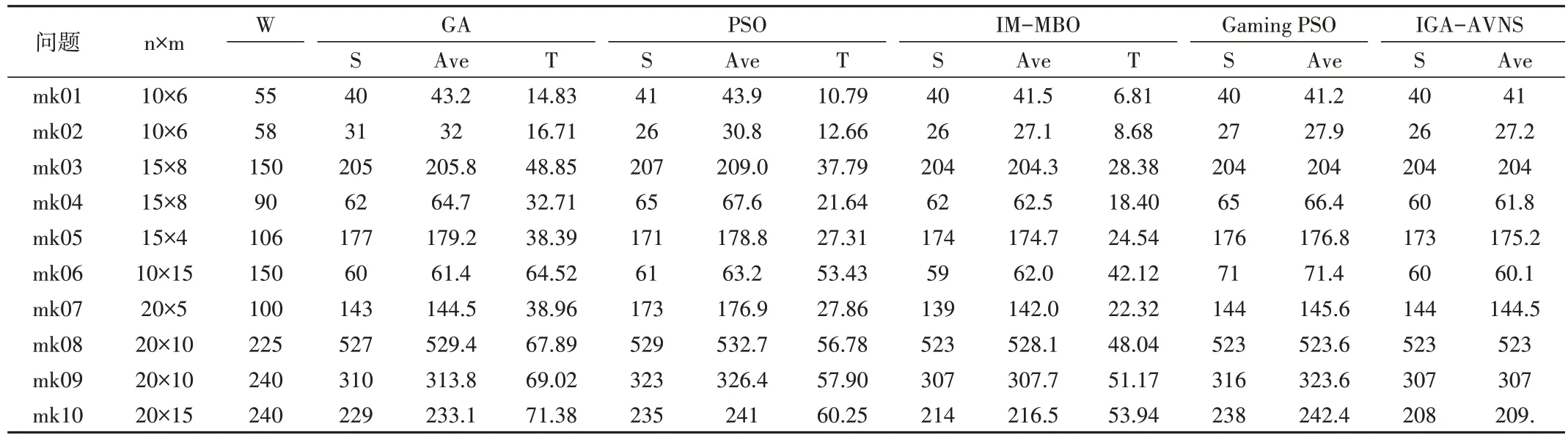
Table 2 Comparison of efficienty of main heuristic algorithms表2 主要启发式算法效率对比

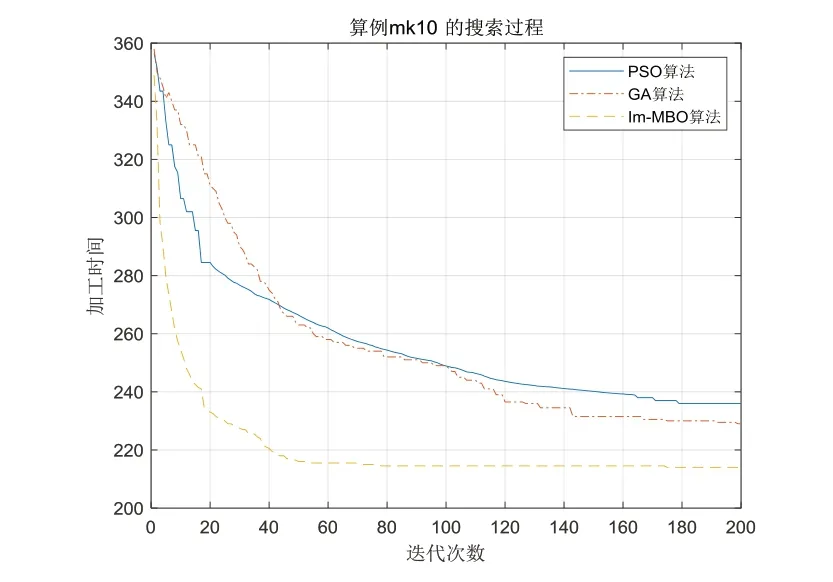
Fig.8 Solution process of the three algorithms图8 3种算法求解过程

4 结语

为了解决云制造模式落地存在的问题，使制造产业通过云制造模式充分利用制造资源，提升生产能力上限，进而提高生产效率、缩短生产时间，降低成本和能耗，推动中国制造产业高质量发展。本文主要研究了云制造模式下的柔性生产调度问题，提出了云制造模式调度框架；对MBO 算法进行了优化，在问题求解过程中使用了新的种群编码方式，利用3 种种群初始化策略按比例生成优质种群；采用新的进化方式并且引入变邻域搜索，提升算法的全局和局部搜索能力；最后用常用的10 个柔性调度案例验证了IM-MBO 算法的正确性和有效性，有利于提升云制造环境下的生产速率并降低生产成本。后续会考虑云制造环境下的动态订单调度问题，并采用IM-MBO 算法将云制造模式扩展成多目标问题求解，以更加符合实际需求。