二阶多智能体碰撞避免与连通性保持方法研究
2023-01-07周瑞敏王瑞尧周志青
周瑞敏,王瑞尧,周志青
(平顶山学院 信息工程学院,河南 平顶山 467036)
0 引言
多智能体系统以其特有的分布性、协调性和鲁棒性,在智能物流、军事防御、灾害救援等领域得到了大量的应用,并成为近些年来分布式控制系统的主要研究热点.目前,针对多智能体系统的研究,主要从模型本身出发,根据智能体之间的拓扑连接情况,采用相应控制方法,在保证系统性能要求的同时完成一致性、编队、包围等任务[1].
当可移动智能体在执行任务时,由于通信时滞、传感器失灵、外界未知干扰等因素,导致智能体不能及时获取自身及周围环境的状态信息,进而可能造成智能体与其他物体发生碰撞,不能完成协同任务.相对于静态障碍物的躲避,智能体之间的碰撞避免更具难度和挑战性.目前针对多智能体领域的碰撞问题,主要解决方法有基于零空间的行为控制方法、预测控制方法、人工势场方法等.基于零空间的行为控制方法通过将任务进行等级划分,然后将低级任务投影到高级任务的零空间上,以达到碰撞避免的目的[2-5].预测控制主要是在求解控制器之前,考虑添加智能体之间距离约束,进而实现智能体之间的距离大于相应的安全距离[6-7].相对于前述两种方法,人工势场法的原理和实现方式更为简单,主要是通过确定势场范围,当另一个智能体进入自身的势场范围内时,智能体会受到排斥力的作用,以使智能体相互脱离其势场范围[8],[9]1253.文献[9]1253首次提出了基于距离和速度的碰撞避免思想,将可能发生碰撞的区域大大减小.文献[10]在速度和不确定性动态未知的情形下,提出了基于观测器的滑模控制律,实现了系统跟踪误差的收敛性,并能保证智能体的相对距离满足指定约束.但上述文献只考虑了防碰撞问题,没有考虑智能体之间距离在势场半径附近时,势场排斥力时有时无带来的抖振现象.
对于智能体自身配备检测和通信设备的情形,其通信能力有限,智能体之间距离不能过大,否则会导致通信中断[11-12].为了同时解决碰撞和连通性中断问题,针对二阶双积分多智能体,文献[13]2449提出了编队控制律,并给出了势场函数参数的范围.文献[14]5898针对具有严格反馈的多智能体系统,提出了实际时变编队控制律,同时保证了势场函数的连续性,避免了抖振现象.文献[15]针对水上无人船模型,提出了基于输出反馈的协同控制律,可以同时保证碰撞避免和连通性保持.
基于以上论述和分析,针对二阶多智能体,笔者提出了具有去抖振的自适应碰撞避免和连通性保持方法,主要创新及贡献总结如下:
1) 同时解决了碰撞避免和连通性保持问题,丰富了多智能体的编队控制安全理论,并在势场函数设计过程中,引入相对速度以减小势场力对编队的不利影响.
2) 相对于文献[14]5904,考虑智能体半径,提出了更为简单的去抖振方法,以消除势场力在势场边界时的抖振现象.
1 图论与问题描述
1.1 图论
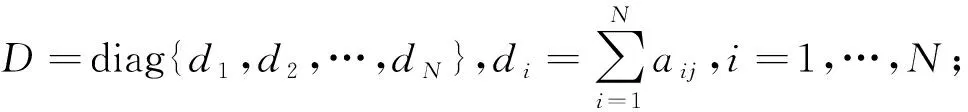
1.2 问题描述
考虑多智能体系统在三维空间运动,跟随者和虚拟主智能体模型描述如下:
(1)
(2)
其中,xi∈R3和x0∈R3分别为跟随者和虚拟主智能体的位置状态向量;vi∈R3和v0∈R3分别为跟随者与虚拟主智能体的速度状态向量;ui∈R3为跟随者的控制输入.
为了描述期望编队队形,引入变量τ=[τ1,τ2,…,τN],其中τi∈R3为智能体i与虚拟主智能体的期望位置偏置,定义编队跟踪误差如下:
(3)
其中,exi为位置跟踪误差向量,evi为速度跟踪误差向量.为了便于分析和描述,定义
(4)
笔者的目标是针对模型(1)和(2)设计控制方法,以实现变量τ描述的期望编队,同时保证智能体之间不发生碰撞,且智能体之间距离不超过最大通信距离.
2 控制方案设计
2.1 碰撞避免设计
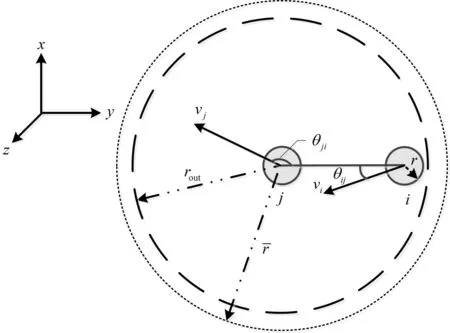
图1 碰撞避免原理
Ψca=
(5)

(6)
(7)
考虑到可能同时存在多个智能体与智能体i发生碰撞,则智能体i的碰撞避免控制律为:
(8)

2.2 连通性保持设计

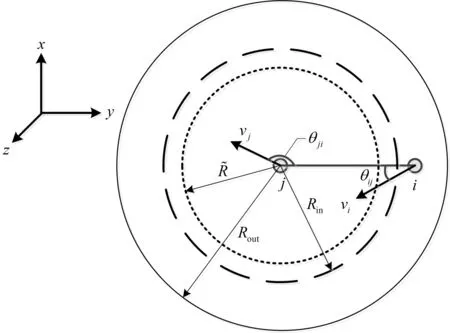
图2 连通性保持原理
Ψconn=
(9)
其中,自适应动作函数
(10)
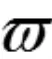
(11)
则针对智能体i的连通性保持控制输入为:
(12)
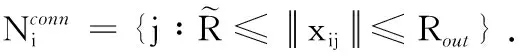
2.3 连通性保持设计
根据状态反馈原理及加性原理,结合公式(8)和(12),设计带有碰撞避免和连通性保持的编队控制律为:
(13)
其中,k1和k2为待设计的控制器参数.
3 理论分析
定理1 在编队控制算法(8)、(12)和(13)作用下,其中k1=-1,k2<0,则系统(1)能够实现零稳态跟踪误差,同时保证碰撞避免与连通性保持.
证明选取半正定类李雅普诺夫函数如下:
(14)
式(14)对时间t求导可得:
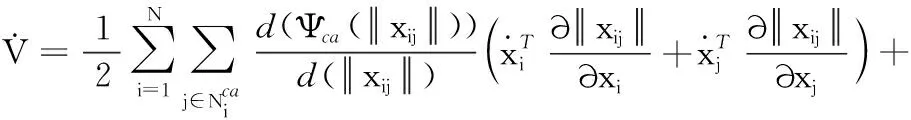
(15)
令
(16)

(17)
后续稳定性,碰撞避免和连通性保持的证明可参考[9]和[13],过程类似,此处不再列出,证毕.
4 数值仿真
选取由5个跟随者和1个虚拟领导者组成的多智能体系统,连接情况如图3所示.
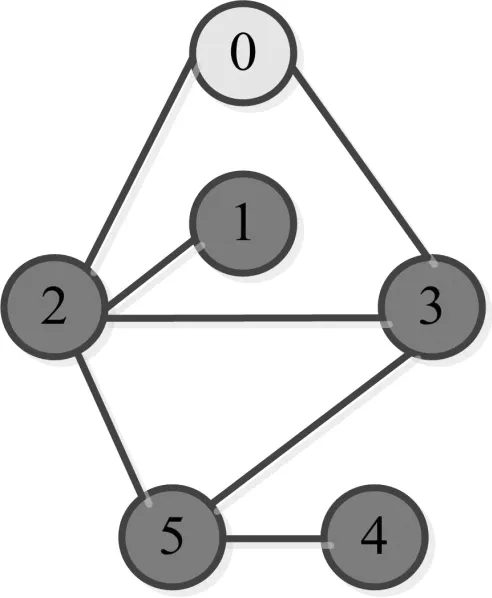
图3 通信拓扑
主智能体的初始速度为[0.4,0.4,0.4]T,初始位置为原点,跟随者的初始状态如下:
与虚拟主智能体的期望偏置位置为:
从图4可以看出,5个跟随者形成了五角星编队队形.图5中两个子图分别给出了有无碰撞避免(CA)和连通性保持(CP)时智能体之间距离的变化趋势,从图5(a)可以看出,无碰撞避免和连通性保持算法加入时,智能体发生了碰撞和连通性中断;反之,智能体间距离均大于2r,且小于Rout(见图5(b)),验证了所设计的碰撞避免算法和连通性保持算法的有效性.图6给出了编队位置跟踪误差和速度跟踪误差变化趋势,表明当t→∞时,系统可以达到零稳态跟踪误差.为了说明笔者所提去抖振方法的有效性,给出了有无去抖振时的速度变化仿真结果,其中图7(a)为有去抖振作用的智能体速度变化曲线,图7(b)为无去抖振作用加入的智能体速度变化曲线.对比可以看出(0~10 s),在去抖振作用下,智能体速度变化相对平缓.
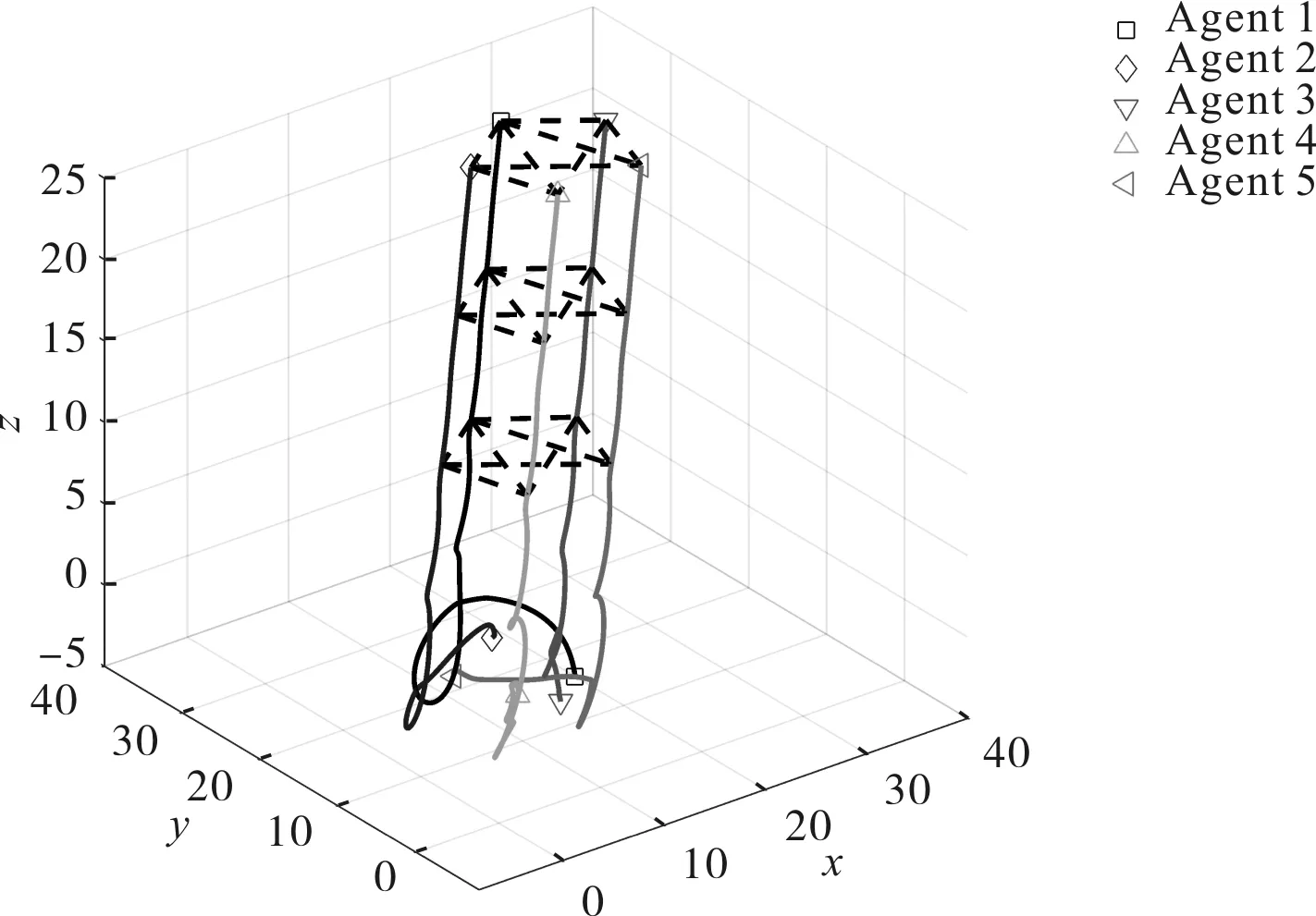
图4 智能体运动轨迹
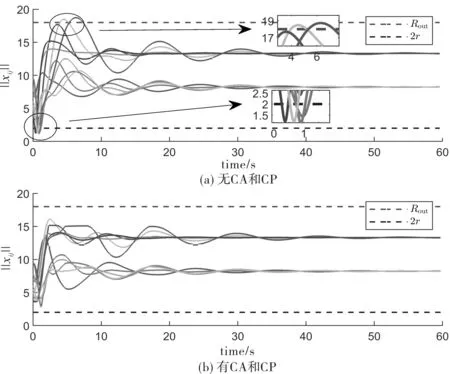
图5 有无CA和CP时智能体间距离

图6 位置和速度跟踪误差
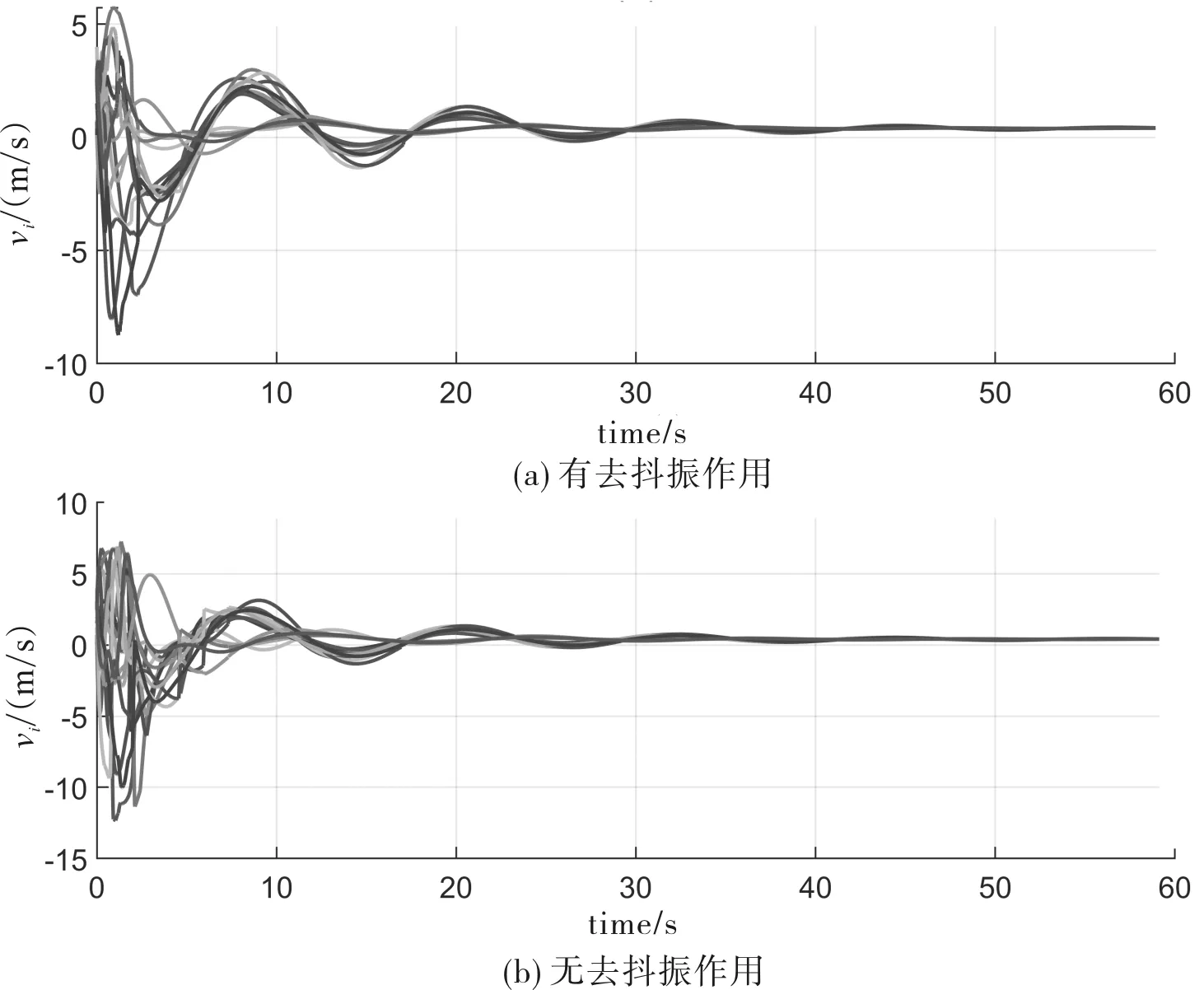
图7 有无去抖振加入时智能体速度
5 结论
笔者在人工势场基本原理的框架下,给出了碰撞避免和连通性保持算法,相比于其他结果,提出了较为简单的去抖振方法,并且所设计的势场函数可以根据相对速度的大小,自适应调节势场力,以达到碰撞避免和连通性保持的目的.为了验证所提算法的有效性,最后进行了仿真实验验证,结果表明所提的方法可以实现编队零稳态跟踪误差,并且同时保证碰撞避免和连通性保持.
