多维度单分子成像研究进展

李孟帆，陈剑威，石 伟，傅 爽，李昀泽，罗婷丹，陈俊帆，李依明

（南方科技大学 生物医学工程系, 广东 深圳518055）

1 引 言

光学显微镜作为人类利用光线进行生命探索工具的历史悠久，早在300多年前，列文虎克就用自制显微镜，对植物、动物细胞以及灰尘进行观察，证明了微生物的存在，揭开了生命最小单位的神秘面纱。随着科学理论的发展以及技术的进步，19世纪天文学家阿贝发现，限制显微镜成像极限的不再是透镜的放大倍数，而是系统对点光源会聚成像形成的圈状衍射光斑，这种光斑被称为艾里斑（Airy Disk）。即使是无限小的点光源经过透镜后也只能形成有限大小的艾里斑，当两个点光源离得比较近时就难以将它们分辨开。这种判断方法也被称为瑞利判据，在可见光范围内普通物镜的分辨能力约为200 nm。

近年来，随着对荧光分子开关的研究不断深入以及激光调制技术在生物医学领域的应用，已经出现了数种能够突破光学显微极限达到高分辨率成像的方法，包括：结构照明显微镜（SIM）[1-2]、受激发射损耗显微镜（STED）[3-5]，以及单分子定位显微镜（SMLM）[6-11]。其中，SIM技术的成像速度快，但分辨率提升较低；STED技术在分辨率和速度上表现都比较好，但缺点是对样品的光损伤较大。SMLM由于在三者中具有最高的分辨能力且不需要复杂的光路设计故被广泛应用于细胞器以及蛋白质结构的研究。但受限于其成像原理，SMLM的成像速度慢且对标记物要求较高。针对SMLM的上述缺点，近年来许多应对这些挑战的设计思路被提出，譬如：利用上转换荧光材料实现低能耗超分辨成像（STED）[12-14]，以及采用DNA互补特性实现任何染料都可成像的DNA-PAINT技术[15-16]等。

常规荧光显微镜在对目标荧光激发成像时往往会因为标记密度过大导致在受到激发且同时发光的情况下成像不可分辨。譬如线粒体内脊、微管以及核孔蛋白等纳米尺度下的结构在宽场成像中模糊不清。单分子定位显微镜则是通过激光不同步激活、激发，单分子荧光探针短时间内发生闪烁，保证相机的每一帧都能获取到稀疏少量的荧光点图像。通过计算机处理，解析获得的每一帧单分子信息，再将这些信息重新组合在一个图像空间上，最终获得高分辨图像。

光学系统的冲击响应被称为点扩散函数（PSF），其形态由光学系统的调制和发光点的物理性质决定。譬如在光路中插入柱面镜、起偏器、相位板以及自适应光学器件，又或是点光源本身的特性如荧光探针的发射波长、空间位置、朝向等参数都会使PSF形态产生变化。因此，从单分子图像中分析出单分子点所包含的信息就是单分子成像方法的核心。点扩散函数工程（PSF Engineering）是将单分子点信息编码进PSF，已成了热门研究课题。

自单分子定位方法诞生以来，出现了许多的PSF工程设计与实现方法，也逐渐出现了能获得某一参数的更精确信息或是能够同时获取多种信息的PSF设计。本文将阐述多维度的PSF工程技术，主要概括了目前的多维点扩散工程在单分子定位技术中对荧光点各个信息的解析，包括三维位置、发射波长以及偶极子朝向等，并简单介绍了单分子信息提取方法，最后讨论了多维度的PSF工程目前在显微成像中的优缺点，并对其在未来的发展进行展望。

2 点扩散函数的多维度信息提取

2.1 单分子二维定位

在宽场成像中，由于所有荧光分子同时发光，纳米尺度的生物结构会被掩盖（图1（a）），因此只有200 nm分辨率 。而单分子成像，则利用了荧光分子的开关特性，使荧光探针不同步发光。在持续的激发光照射下，一小部分的探针被“打开”，稀疏分布的单分子图像将会被相机收集（图1（a），t1）。而在下一时刻已经被“打开”的单分子可能会被关闭，同时另一部分的探针将被“打开”（图1（a），t2）。部分单分子荧光不断地“打开”、“关闭”，大量的稀疏单分子图片将被采集，通过解析它们所蕴含的信息，最终便可以重构成一张高密度高分辨率图像。单分子二维定位则通过计算每一帧图像中PSF质心[17]的位置并进行高斯拟合[18]，从而得出荧光探针的二维坐标信息[19-21]，最终组合为高分辨率的二维图像（图1（b））。理论上每一个单分子图像都有一个唯一的坐标位置，然而在每一次成像中，光子因遵从泊松分布而具有一定概率性，因此定位结果也具有不确定性。在这种情况下一般能获得20 nm的二维定位精度。

图1 单分子二维定位[21]。(a)在采集步骤中，将会获取稀疏分布的单分子闪烁图像；(b)分析步骤中，从单帧图像中准确定位的单分子二维位置，以及所有单分子点的合成图像。Fig. 1 Two-dimensional localization of a single molecule [21]. (a) In the acquisition step, sparsely distributed single molecule images are recorded; (b) in the analysis step, the two-dimensional coordinates of the single molecules are precisely localized in each frame and then accumulated to reconstruct the super-resolution image

2.2 单分子三维位置信息的提取

生物研究中，对细胞器空间分布以及蛋白质三维结构的研究具有重要意义，因此获取单分子三维位置尤为重要。沿荧光探针不同轴向位置单分子图像的变化情况如图2（a）所示。然而，在焦点附近的标准PSF随轴向位置改变而产生的形态变化非常不明显 （图2（a））。同时，处于焦点上方的单分子点产生的图像与下方的单分子图像形态过于相似，难以区分单分子点轴向位置是处于焦平面上方还是下方。所以，标准PSF通常不能获得较为精准的定位。

在早期Huang等[22-23]通过巧妙地在物镜后焦面插入柱面镜来打破焦点上下难以区分的困境。通过人为引入散光像差（astigmatism）将子午面焦点与弧矢面焦点错位，在焦点平面上下产生横、纵向拉伸的PSF（图2（b）），拉伸幅度会随着单分子点与焦点距离的不同而有所不同。她们采用椭圆高斯拟合精准定位单分子点的三维位置，焦点位置横向和轴向的定位精度为10 nm和22 nm。由于其在焦点附近具有较高的轴向分辨率以及实现方式较为简单，时至今日这都是单分子成像方法的最常用PSF工程之一。

比起借助已有透镜来调制不同形状的PSF，使用相位板（phase plate）、空间光调制器（Spatial Light Modulator，SLM）和可变形镜（Deformable Mirror，DM）[24]设计不同形状的PSF更灵活。2009年，Moerner实验室开发出了复杂的PSF并用于单分子成像领域，他们基于高斯-拉盖尔模PSF调制理论[25-26]，计算出一种旋转传播的PSF及其所需的相位，并先后将SLM和相位板放置在物镜后焦面上，成功将轴向位置信息编码进PSF中，这种方法被命名为双螺旋（Double-Helix,D-H）PSF。图2（c）两个旁瓣光斑会随着单分子点的轴向位置变化而发生旋转[27-28]。随后越来越多具有创意的PSF被应用在单分子成像领域，例如在后焦面上放置相位斜坡（Phase ramp）产生能够发生相对滑动的PSF[29]（图2（d）），单点旋转的螺旋（Corkscrew）PSF[30]（图2（e））， 利用艾利光束的自弯曲性[31-32]开发的基于双通道无旁瓣PSF[33]（图2（f）），图2（g）为SLM调制下的光路布局图。

图2 各PSF在不同轴向位置的变化及在SLM调制下的光路布局。（a）标准PSF；（b）散光PSF；(c)双螺旋PSF[27-28]；(d)相位斜坡PSF[29]；(e)螺旋PSF[30]；(f)自弯曲PSF[33]；(g) SLM调制下的光路布局Fig. 2 Changes of each PSF at different axial positions and optical path layout for SLM modulation. (a) The standard PSF; (b)astigmatism PSF; (c) double helix PSF[27-28]; (d) phase ramp PSF[29]; (e) spiral PSF[30]; (f) self-bending PSF[33]; (g) optical path layout for SLM modulation

在上述PSF工程出现的数年间，已经出现了许多能够随着三维位置出现较大变化的PSF。它们虽然能够以各种形式解码出单分子的三维信息，不过需要一个统一的指标来衡量PSF的定位精度。相机像素上收集到的光子数量在统计上服从泊松分布，而克拉美罗下界（Cramér-Rao lower bound，CRLB）是统计学上衡量无偏估计量是否有效的重要指标，如果一个拟合器有效，那么其拟合结果的标准差应该接近CRLB，那么也可以说CRLB是该拟合器能达到的拟合精度极限[34-35]。

2014年，Shechtman等将光瞳函数的55项泽尼克（Zernike）多项式幅值作为优化参数[36]，以CRLB作为指标构建了一项损失函数：

其中i为CRLB的优化维度，z为单分子点轴向位置。利用该损失函数，Shechtman等在1.5 μm的轴向范围内优化出了一个整体三维精度最优的鞍点（Saddle Point, SP）PSF，并用相位板实现了该PSF，证明了其在三维坐标具有更高的定位精度。利用CRLB的优化方式具有维度选择性，譬如只以x、y的CRLB作为优化指标可以得到在二维坐标下定位精度较高的PSF或者只优化z维度CRLB得到轴向坐标定位精度较高的PSF等。

2015年，Shechtman等以轴向景深为优化目标，得出了可调节轴向定位范围的Tetrapod PSF[37]（图3，彩图见期刊电子版）。与1 μm轴向定位景深的散光调制PSF相比，其景深能达到10 μm，并实现了在微流通道（Microfluidic channel setup）中对单分子点追踪的应用。将光瞳函数的Zernike多项式系数作为优化参数的方法通常都会得到与Tetrapod类似的PSF。虽然它们能获得较高的拟合精度，但是由于它们的光子分布较大，单个PSF可能占据几十个像素的宽度。当分子密度较高时，常会发生多个PSF重叠现象，传统的PSF提取程序很难将每个PSF完整分割。因此，这一类的PSF通常应用于密度较为稀疏的单分子追踪（Single Particle Tracking，SPT）或是平面轮廓分析[38-41]。近年来出现将深度学习应用在重叠PSF的分析方法[42-43]，使得大景深定位成像成为可能。

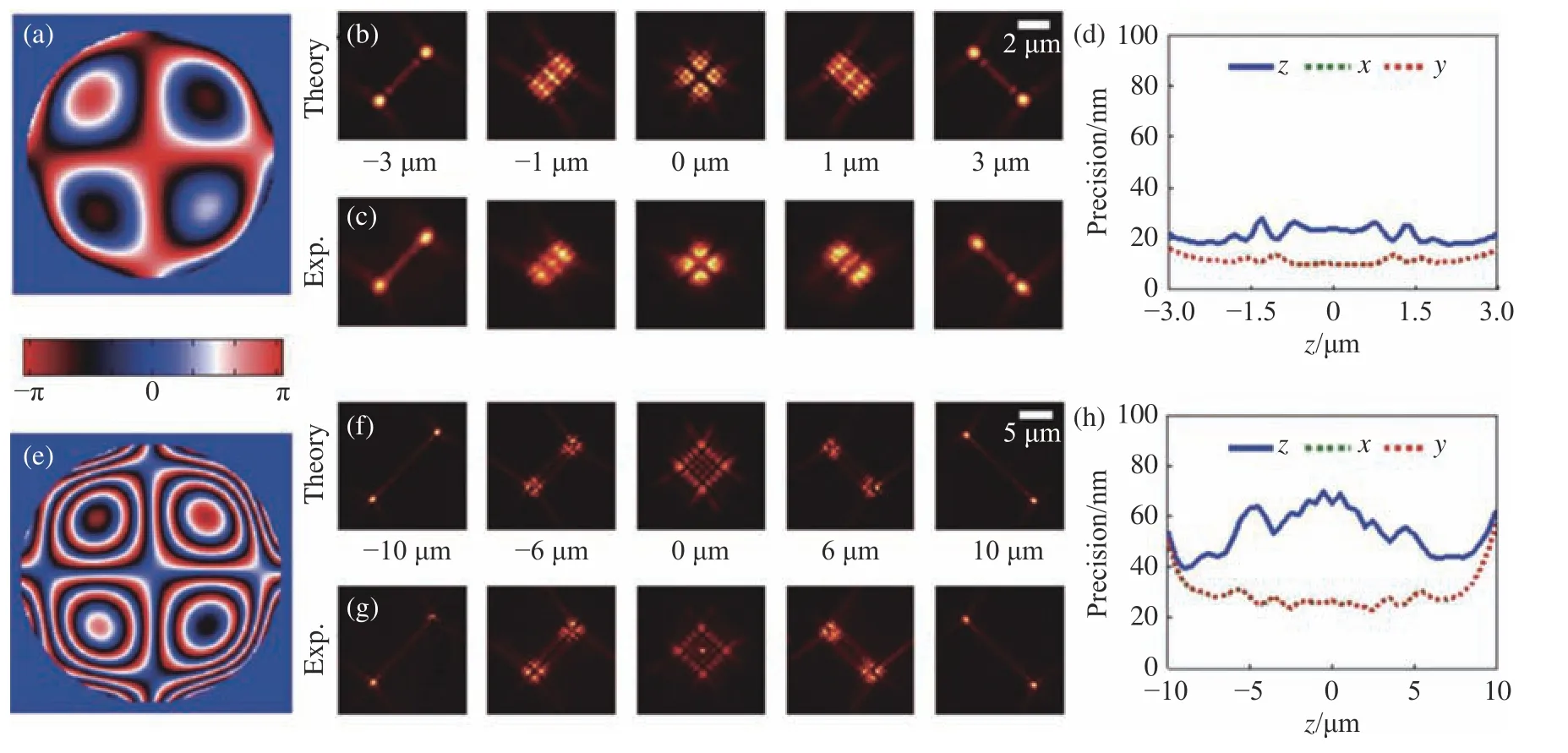
图3 不同景深优化下的Tetrapod PSF[37]。6 μm优化景深下的光瞳函数（a），理论PSF（b），实验PSF（c），定位精度（d）。（e）～（h）与（a）～（d）相同，但是为10 μm优化景深下的Tetrapod PSF。Fig. 3 Tetrapod PSF optimized at different depths of field[37]. (a) The pupil function, (b) theoretical PSF, (c) experimental PSF,(d) localizing accuracy of Tetrapod PSF optimized for 6 μm depth of field. (e)～(h) The same as (a)～(d), but for Tetrapod PSF optimized for 10 μm depth of field.

除了从荧光探针PSF中提取三维信息外，对激发光调制也能实现单分子三维定位。2017年Balzarotti等基于探测局部最小激发光，借助doughnut PSF提出了MINFLUX成像技术，其横向分辨率能达到1 nm[44]。2020年，Klaus等采用三维空心激发光PSF，进一步使用MINFLUX实现了三维定位，其各项同性的定位精度甚至达到了3 nm[45]。

2.3 单分子图像的波长信息提取

现代荧光标记技术十分灵活，使用不同发射波长的荧光探针标记不同的细胞结构进行多色成像可以研究各细胞器的空间结构及相互作用。一般的实现手段是在光路上放置二向色镜，将物镜接收到的发射光分为两路并分别成像在相机的两个区域，根据两区域对应位置上的PSF强度比值即可推断出该点的发射波长。Ilaria等根据这种方法实现了PtK2 细胞的三色成像[46]。

虽然多通道分色能够区分发射波长十分接近的荧光探针，但是这也意味着单一通道接收到的光子数降低，与此同时，其拟合精度就会下降，而且采用不同发射波长的探针可能都要重新挑选二向色镜的分光波长，适用性并不普遍。2016年，Broeken等借助衍射原理，通过SLM调制的稀疏光栅，令原本只有一个光点的PSF衍射为+1、-1和0级衍射亮点，测量1级极大值间隔获取其波长大小。在1 000光子数时其波长拟合精度可达到10 nm，实现了二维位置和荧光波长的同时测量[47]。2016年，Smith等借助SLM更进一步设计了弯曲光栅的后焦面调制，如图4（a）～4（b）所示，开发出了能够同时拟合三维位置信息和波长信息的PSF[48]。该设计同样是利用1级衍射距离判断波长，同时在不同的深度会发生显著变化（图4（c）），在平均光子数为800时其拟合光谱精度达10～20 nm，轴向精度达25～50 nm。

图4 同时测量单分子的发射波长与三维位置 [48] 。（a）光路设计图，SLM放置在后焦面上；（b）弯曲光栅的光瞳函数；（c）3种波长在不同位置下的PSF分布，波长越长2个旁瓣的距离越远Fig. 4 Simultaneous measurement of emission wavelength and 3D position of single molecules[48]. (a) Optical path design with an SLM placed on the back focal plane; (b) pupil function of curved grating; (c) PSF distributions of three different wavelengths at different localizations. The longer the wavelength, the farther the distance between the two side lobes

除了采用干涉、衍射方法区分波长外，还有基于色散原理设计PSF。Zhang等[49]通过在双通道分别插入柱面镜和分光棱镜的方法，实现了三维位置和荧光光谱的同时定位，并用该方法对差别为10 nm的4种染料进行无串扰三维成像。在SLM中，即使施加电压相同，不同波长的光经过后相位改变也略有差别，针对这一问题，Shechtman等通过最小二乘法计算出一种波长适应的SLM电压[50]，在同一个SLM调制下，实现了红光和绿光具有45°角度差的Tetrapod PSF，并进行了微管-线粒体的双色成像。2019年，Hershko等基于上述思路，通过神经网络在仿真系统中优化出一组具有特定波长响应SLM电压[51]，实现了同一视场分辨4种波长的单分子。

随着深度学习在成像领域的发展，许多以往不被注意的细节都能被机器学习解析出来。2019年，Kim等将两份由不同染料单独标记的原始图片放入神经网络中进行训练[52]，让网络学习到各PSF的轴向和颜色细节特征，然后应用在未知样品的三维位置定位及颜色分辨上（图5）。Kim的报告进一步证明了即使对于标准PSF，也能解析出更多的信息，展现了计算科学的发展对显微成像领域的推动作用。

图5 基于人工神经网络的信息提取方法[52]Fig. 5 Information extraction method based on artificial neural network [52]

2.4 基于单分子图像的偶极子朝向的参数提取

在大部分的PSF建模过程中，通常假设单分子点发射都是各向同性的。然而在许多情况下单分子点会表现出各向异性，物理层面上表现为具有方向指向的偶极子。对于自由旋转的单分子点来说，由于其朝向每时每刻都在改变，故在相机曝光时间内能够收集到的光在各个方向的光强比例大致相同。但是如果单分子点被限制在某个方向上时偏振光强分布会发生偏移，对应的PSF的中心会出现大约100 nm的偏差[53-54]。在如图6（e）所示偶极子模型中，其在xy面的偏转角称为方位角(azimuthal angle)，表示为φ,与光轴之间的夹角称为极角(polar angle)，表示为θ，同时由于偶极子可能并未完全固定，自身也会发生旋转振动，转动角度称为转动角α。当转动角较小时，偶极子光强分布较不均匀，反之，则更偏向于各向同性，如图6（a）～6（c）（彩图见期刊电子版）。此外，极角大小也会影响PSF偏移量的大小（图6（d））。因此，获取偶极子朝向可以补偿PSF的横向偏移，提高定位精度；而偶极子朝向在研究膜蛋白相互作用以及排列方式上也具有非常重要的指示作用[55-57]。

图6 偶极子方向引起的定位偏差[53]。（a） 转动角、极角、方位角分别为15°、45°、0°时单分子点的PSF xz切面（左图），xy切面（右图），以及其定位偏差；（b）极角、方位角与（a）相同的情况下转动角为60°的PSF；（c）和（d）分别为不同转动角，极角产生的横向偏移值；（e）转动角、极角、方位角在偶极子中的物理意义Fig. 6 Localization deviation caused by the dipole’s direction[53]. (a) PSF xz section (left) and xy section (right) of single molecule with a rotation angle, polar angle and azimuth angle of 15°, 45° and 0° respectively, and corresponding localization deviations; (b) PSF with the same polar angle and azimuth angle as (a) and rotation angle of 60°. (c) and (d) are the lateral offsets generated by different rotation angles and polar angles, respectively; (e) physical meaning of rotation angle, polar angle and azimuth angle of the dipole

2012年，Mikael等尝试通过双螺旋PSF来获得偶极子朝向[58]，他们运用偏振分束棱镜将两正交偏振光分开实现双通道成像（图7，彩图见期刊电子版）。虽然利用各通道的光子比例LD（Linear Dichroism）可以大致推断出方位角φ的朝向，但偶极子极角θ还未确定。接着，他们根据双螺旋PSF特征引入了旁瓣不对称性LA（Lobe Asymmetry）用以描述极角大小。LA指标的引入，解决了只考虑光子比率LD时定位结果简并的问题。当两参数确定时能够得到唯一的偶极子朝向结果。

图7 基于双螺旋PSF的偶极子方向定位方法[58]。（a）光路布局；（b）和（c）分别为两个偏振方向的成像通道，它们的光瞳函数分别为（i）、（ii）；（d）上下图分别为水平和垂直通道的PSF；（e）和（f）分别为LA、LD指标，只考虑LA指标时会出现4种可能的朝向结果。红色和蓝色分别代表透射通道和反射通道的LD指标Fig. 7 Dipole orientation localization method based on double helix PSF[58] . (a) Optical path layout; (b) and (c) are imaging channels in two polarization directions, respectively, and their pupil functions are (i) and (ii) respectively; (d) the upper and lower figures are PSF of horizontal and vertical channels, respectively; (e) and (f) are LA and LD indicators respectively. There are four possible orientations when only the LA indicator is considered. Red and blue represent LD indexes of transmission channel and reflection channel respectively

涡旋相位板(Vortex phase plate)是一种能将高斯光束调制为空心圆环的螺旋递增相位板，通常应用在STED显微镜[59]的激发光整形中。2021年，Hulleman 等将涡旋相位板放置在成像光路的傅立叶面上[60]，调制出Vortex PSF，如图8（a）（彩图见期刊电子版）所示。Vortex PSF与标准PSF相比，其偶极子朝向拟合精度有所提高，如图8（b）～8（c）所示，由于PSF较为紧凑，单分子图像的信噪比得到提高。他们利用这种方法实现了λ-DNA的偶极子朝向和三维位置的同时定位（图8（d）（彩图见期刊电子版））。

图8 基于vortex PSF的朝向与三维位置同时定位[60]。（a）Vortex PSF光路；在4 000个光子10个背景光子的单分子图像中，（b）方位角φ和（c）极角θ的CRLB；（d）λ-DNA的二维位置及方位角，伪色代表该点方位角，大小如左下角Fig. 8 Simultaneous localization of the single-molecule orientation and three-dimensional location based on vortex PSF[60] .(a) Vortex PSF’s optical path; CRLB of azimuth angle (b) and polar angle (c) in single molecule imaging with 4 000 photons and 10 background photons; (d) 2D position and azimuthal angle of the λ -DNA. The false color represents the azimuthal angle, as shown in the lower left corner

2.5 4Pi显微镜的相位提取

20世纪90年代，Hell等提出了一种双物镜成像系统架构[61]。与单物镜系统相比，其几乎接收了全立体角（4π）的荧光并发生自干涉，因此被称为4Pi显微镜。其轴向分辨率比宽场时提高了数倍。将单分子定位成像法与4Pi显微镜的结合可使轴向分辨率达到纳米级别[62]，这种成像方式被称为4Pi-SMLM。利用分束器将上下物镜的光重叠并进行干涉成像是4Pi-SMLM的光路设计特点[63-64]。将上下通道分别延迟不同的相位并在多个通道成像，各个通道的单分子图像相对光强反映了其干涉相位。由于各通道光强对于相位变化十分敏感，轴向分辨率能达到单物镜系统的6～10倍，实现亚10 nm精度的轴向定位[10]。

在4Pi PSF中存在4个相互独立的维度，即x、y、z和两物镜接收到单分子荧光的相位延迟φ。因此，建立4Pi PSF模型就需要获取各个轴向位置和干涉相位下的4Pi PSF，然而这需要精确的相位延迟方法，这在操作上是难以实现的。2020年Li等在相同光路中（图9（a）），通过IAB模型从轴向位置中解耦出干涉相位项，从实验采集的PSF中建立更真实的4Pi PSF模型[65]，如图9（c）所示。IAB模型可以将四通道实验PSF分成3个与相位φ无关的矩阵Ι、Α、Β，只需要校准3个三维矩阵就可以完整表达一个实验型的四维的4Pi-PSF，避免了对四维4Pi-PSF的直接校准。解决了由于温度变化对光程的改变所引起的定位偏移，结果证明了IAB模型能够达到理论定位精度，如图9（b）（彩图见期刊电子版）所示。

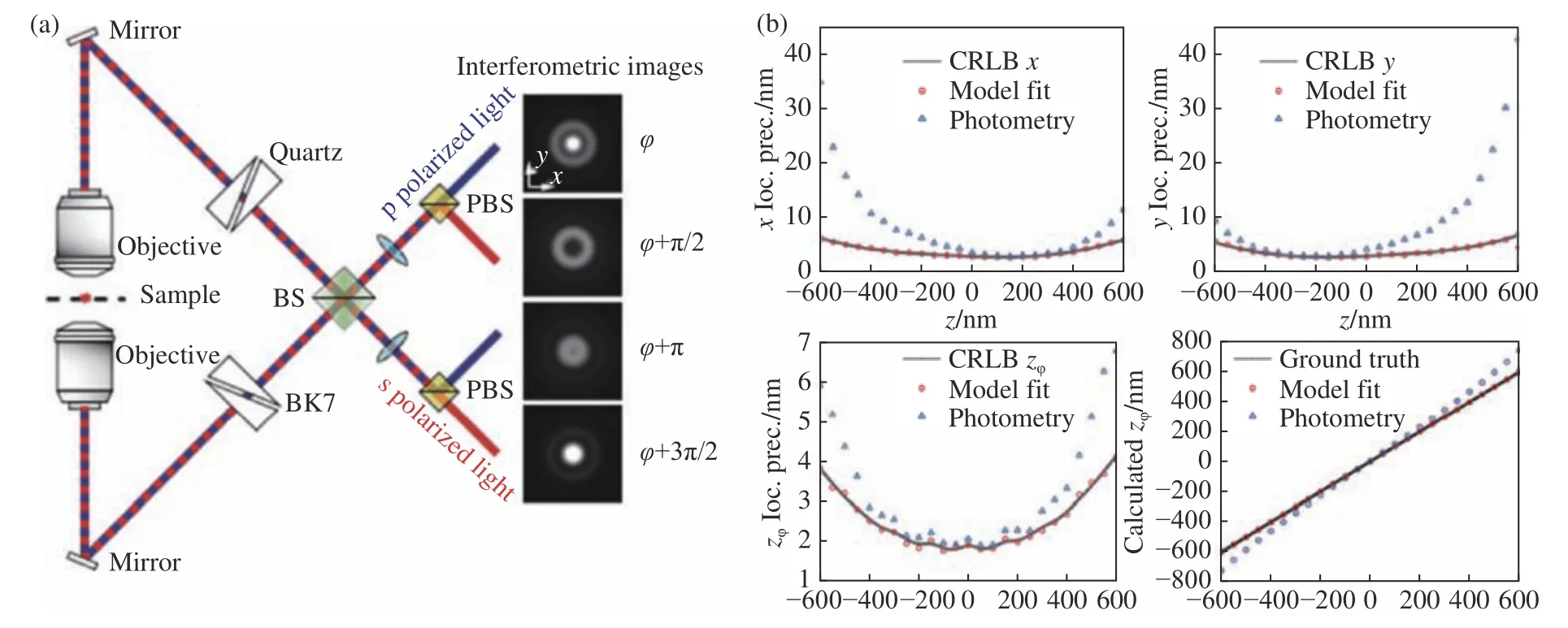
此外，IAB模型还克服了光度法（photometry）在高数值孔径物镜产生定位偏差的问题。由于4Pi实验装置是一个多通道光路，天然适合进行多色单分子成像。2022年，Chen等提出只需在原有4Pi实验装置中π/2和3π/2光路插入滤光片，就能实现目前最简洁的多色4Pi成像系统[66]，并且相比传统的多色4Pi方法[67]提升了光子利用率。

3 点扩散函数模型和分析方法

3.1 点扩散函数建模

3.1.1 高斯模型拟合

虽然从光学计算角度出发，点光源在像平面的光强分布并非是高斯分布，但是因为艾瑞（Airy）光斑与高斯的形状相似，且高斯模型的计算更为简单而被广泛使用[68]。二维高斯计算模型为：

式（2）中，x0,y0为 高斯中心位置，σ为二维高斯宽度。

不过高斯拟合结构简单，对于存在由像差、特定偏振等导致的不对称的PSF并不适用。随着单分子点远离焦点位置，艾瑞光斑会显示出明显的衍射环图案，高斯模型已不足以描述其变化。总的来说，高斯模型拟合在单分子点处于焦点附近百纳米的对称PSF时，能够实现理论的二维定位精度。然而在复杂的光学调制情况下，还需要更为真实的PSF模型。

3.1.2 三次样条插值的实验点扩散函数模型拟合

为了还原PSF的精细结构，通常根据光场分布建立PSF模型，对于大数值孔径物镜的成像系统，还需要使用考虑电场偏振的矢量模型[69-70]。然而它们的计算较为复杂，并且光学系统与理想系统存在偏差，通常需要进一步校准。采用图形处理将离散模型连续化的样条插值建模则可以避免这样的问题[71-72]:

其中Δx、Δy、Δz分别为x、y方向像素大小和轴向步长，m,n,p为各维度阶数，ai,j,k,m,n,p为插值系数。每一个位置的PSF强度至多需要64个多项式参与计算。

通过在载玻片上放置荧光珠，移动z轴位移台，可以获得三维实验PSF图像。随后采用插值算法将其连续化，便可建立更真实的插值PSF模型。通过将实验采集图像与插值PSF进行极大似然估计或是最小二乘法，找出最为相似的PSF模型，从而解析单分子图像中的信息。由于插值算法形式固定，因此可以便捷地采用硬件辅助，Li等利用GPU加速计算实现了每秒拟合十万个单分子点的高速拟合[72]。

3.2 神经网络的信息提取

深度学习算法的出现解决了密集且复杂的PSF无法进行单分子定位成像的问题。2018年，Nehme等开发出一套基于卷积神经网络算法的单分子定位工具Deep-STORM[42]。通过提前设置单分子点密度和信噪比生成单分子图片，训练出能够从重叠的单分子图片中还原二维位置的网络。他们演示了通过这种方法解析信噪比较低的仿真图像以及实验成像的微管二维定位。

2020年Nehme等进一步开发出能够进行三维定位的神经网络Deep STORM3D[43]。他们随机生成大量不同轴向位置的高密度单分子仿真图像，不断优化网络直到能够有效还原单分子点的真实位置，训练网络对重叠PSF的三维定位能力，从而实现高密度单分子定位（如图10所示）。通过这种方法他们实现了使用Tetrapod PSF对COS-7细胞上高标记密度线粒体的三维成像。由于训练模型的可选择性，他们也实现了该系统对多种PSF的三维定位。

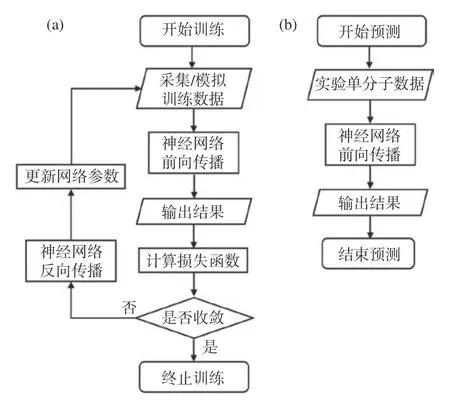
图10 基于卷积神经网络的单分子定位流程图。（a）网络训练步骤；（b）定位步骤Fig. 10 Flowchart of single molecule localization based on convolutional neural network. (a) Network training steps; (b) localizing steps

2021年，Artur等基于上述定位方法，考虑了跨邻帧中所蕴含的信息的相关性(Temporal Context)，开发出下文依赖的深度学习定位方法DECODE[73]。与Deep STORM3D相比，其高密度PSF的定位速度提高了10倍，准确率提高了2倍，在达到理论定位精度的同时对定位结果还可做出不确定度预测。虽然基于深度学习的单分子定位能够实现快速计算，但是每当光学系统发生变化时，都需要花费数小时重新训练网络，不过迁移学习能够缩短新网络建立成本，随着算法的进一步发展，神经网络可能将会被广泛应用于单分子成像中。

4 结束语

在成像技术中，PSF一直都被视为解析单分子点信息的窗口之一。本文介绍了二维单分子定位，多种三维PSF工程设计，以及从PSF提取出的多维度信息，包括荧光发射波长、偶极子朝向、自干涉相位，最后介绍了常用的定位方法。

需要指出的是，对PSF进行改造虽然提高了其对于某一维度的定位精度，但是同时也常需要对另外一些性能做出取舍，譬如增大了PSF面积，或是降低了其他维度的定位精度、缩短了定位范围等。因此，常常需要结合应用场景以及需要解析的单分子信息，挑选合适的PSF进行单分子成像。

由于单分子定位成像涉及到成像原理、材料特性、数据处理等多领域，因此进一步探索多维度信息可以从以下几个方面出发：通过添加额外的光学设备以增加研究维度，譬如通过检偏器测量单分子朝向[48]；通过荧光材料特征反映细胞微环境，解析荧光寿命分辨标记的染料类型[74]；从需要探究的问题中寻找定位维度，譬如单分子追踪中的运动模型参数[75]；从具有误差的图像中还原单分子信息，如校准由于折射率不匹配导致的定位误差[76]；通过高效的算法提升成像质量，譬如多通道全局拟合定位[77]等。总的来说，多维度单分子成像研究是一个多领域、多方向的课题，随着更多学科的加入，已经展现出了巨大的研究潜能和宽广的应用前景。