分辨率、超分辨率与空间带宽积拓展—从计算光学成像角度的一些思考

左 超 ，陈 钱

（1. 南京理工大学 电子工程与光电技术学院 智能计算成像实验室(SCILab), 江苏南京 210094；2. 南京理工大学 江苏省光谱成像与智能感知重点实验室, 江苏南京 210094；3. 南京理工大学智能计算成像研究院(SCIRI), 江苏南京210019）

1 引 言

人类对外界信息的感知80%以上来自视觉。而人眼的信息获取能力受生理结构的限制，在时间、空间、灵敏度、分辨力等方面均存在局限，无法获取遥远距离的信息或者难以看清非常细小的物体。光学成像技术的出现，将客观景物转变为图像，扩展了人眼的视觉特性。例如：望远镜的发明，实现了对宇宙、星空等遥远空间的探索与观测；显微镜的发明，实现了对微观世界如细胞等的观察与分析。由此可见，光学成像系统的发明与研究是为了获取客观世界的图像信息，获取更多的信息量一直是人类追求的永恒目标。

一个光学成像系统的信息量由该系统的视场和分辨率决定[1]。宽视场能够覆盖的观测范围更大，高分辨率能够获得更多的细节信息。顾名思义，宽视场高分辨成像，即成像系统既能够在拍摄到很大的视场范围的同时，又能拍摄到重要且又易被忽略的细节信息。其被广泛应用于众多的科研领域与军事民生领域。比如：在市区广场，车站机场等人流密集的场所，宽视场高分辨率成像系统可以实现全方位安防监控，对密集人群中的可疑人员进行观察甚至跟踪等[2]；在交通管理中，宽视场高分辨成像系统可以对车辆流量，交通安全，路面状况等进行全面的实时观测；在现代军事行动中，越来越要求光学成像系统能够及时获取战场大范围内的详细情报，以满足对军事目标探测、识别、侦测和战场态势感知的需要。在现代生物学领域中，随着研究重点已经由生命体的形态学表型探测逐步转向了细胞和分子基本机制的定量测量，这种格局的转变直接导致对生物光学成像中信息通量的需求在不断增加[3]。例如，神经元作为大脑和神经系统的基础组成部分，它的大小通常是微米量级的，但它的功能连接范围遍及了整个大脑，想要研究整个神经系统的工作机理就必须同时对整个大脑内每一个神经元进行高分辨率成像。再如，细胞生物学、临床快速诊断、药物筛选和细胞功能分析等研究应用一方面需要对群体活细胞进行快速无损的功能检测，另一方面又需要针对单细胞进行亚细胞结构和生物分子水平的动态功能分析以对细胞内基本功能进行解读[4]。然而，复杂生物样本的单细胞研究带来了信息量的指数级增长，伴随而来的更大挑战来自大量的生物信息的获取。简言之就是“小个体”与“大群体”之间的矛盾。一个由数千个细胞组成的肿瘤样本可以在基于集群的研究中进行一次分析，而单细胞水平的研究则需要进行数千次分析。这意味着大量的人力、时间和研究费用。复杂生物系统的单细胞研究在生命科学的各个领域都极为重要，然而有限的技术手段和资源仍然是一个巨大的挑战。因此为了研究这种拥有海量信息的生命科学系统，必须借助于同时具备宽视场和高分辨率的成像工具。

传统光学成像系统的成像过程是一个简单直接的串行过程：场景经过光学透镜系统折射后聚焦投影到传感器，传感器像素和目标场景之间通过建立“点对点”的一一对应关系来获取图像，传感器得到的数据经过数字化处理后形成计算机可显示的图像。这种“所见即所得”的成像模式实质上可以理解为场景强度信号在空间维度上的直接均匀采样记录与再现。在此过程中，成像的分辨率与信息量不可避免地受到光学衍射极限、探测器离散采样、成像系统空间带宽积（Spatial Bandwidth Product，SBP）等若干物理限制：首先，光学系统所能分辨的最小物体特征受限于光的衍射特性，存在瑞利-阿贝物理衍射极限。其与探测光波的波长与成像系统的孔径密切相关，无论使用何种光学仪器，都很难对尺寸小于半个波长（约为200 nm）的微小特征清晰成像。其次，像素是组成数字图像的最小单元，像素数量越多且越细腻，图像承载的信息量就越大，因此像素数量是影响图像品质的重要因素。但受到探测能效、制作工艺、工作条件、光电串扰、功耗成本等因素的限制，光电探测器的像元尺寸无法无限制缩小，规模也无法无限制扩大。最后，对于一个成像系统而言，成像视场越大、分辨率越高，有效像素数量就越多，图像中包含的信息量也就越大。但现有光学成像系统受拉格朗日不变量等因素的制约，空间带宽积大多仅在百万至千万像素量级[2,5-6]。而天文观测、航空航天、生命科学、军事国防等领域迫切需要成像系统满足宽画幅、跨尺度成像，其所需的成像信息量往往要达到亿像素甚至十亿像素级，这是传统成像系统的数十到数百倍。综上所述，基于“所见即所得”的传统成像技术因受光学衍射极限、探测器离散采样、成像系统空间带宽积等若干物理条件的制约，无法满足当今军事和民用领域对高分辨率、宽视场成像应用日益增长的需求。

计算光学成像技术将前端物理域的光学调控与后端数字域的信息处理进行有机结合，为突破传统成像技术的诸多限制性因素提供了新手段与新思路[7-8]。近年来，计算光学成像已发展为一门集信息光学、现代信号处理、计算光学、几何光学等理论于一体的新兴交叉技术研究领域，成为国际上光学成像领域的研究重点和热点，代表了先进光学成像技术的未来发展方向。尽管计算成像的概念形成于20世纪90年代中期，但从本质上而言它并不能算是什么“新事物”。作为20世纪最伟大的工作之一，信息论应用概率论、随机过程、傅立叶分析等数学手段定量分析信号的采集、处理及传输的一般规律。正如其奠基者C.E. Shannon的著名论文A Mathematical Theory of Communication中所说[9]：“通信的基本问题就是在一点重新准确地或近似地再现另一点所选择的信息”。从信息论的观点看来，声学、电学和光学系统都是用来传递信息的，电学系统传递随时间变化的电讯号，而光学系统传递随空间变化的图像[10]。在一个典型的通信系统中，信源消息通过信源编码，信道编码，然后由调制器加载到载波调制信号上通过信道进行传输。在信道的另一端，信号将先经过解调，然后在通过信道解码、信源解码后送到信宿处。经过比较可以直观地看出，近年来快速发展的计算光学成像技术正是信息论在光学成像领域的应用和拓展——场景或物体相当于通信系统中的信源，成像系统相当于信道，最后重建得到的图像相当于信宿。而光信息学，即信息光学就是通信理论中傅立叶分析等一系列数学思想以及系统理论与光学（主要是波动光学）相结合的产物，其研究的是光信号表征、采集、分析、处理以及在自由空间与光学系统中传输的一般规律。

信息光学起源可以追溯到原始光学初期，但获得迅速发展还是最近半个多世纪的事，这得益于20世纪几项重要的发明：信号传输与通讯、激光与光全息、光电信号数字化以及数字信号处理技术。而20世纪末计算成像概念的兴起与快速发展又得益于“可调控”光学器件——包括光源（波长调谐激光器、可编程LED阵列、可编程LCD面板）、光学元件（扫描振镜、变焦透镜）、空间光调制器（SLM，DMD，LCOS）等的出现、先进高分辨高灵敏度光电传感器（sCMOS、EMCCD、SPAD、TOF、偏振相机）、数据处理能力日益提升，存储空间日益递增的计算机/并行处理计算单元、以及最优化理论、压缩感知、深度学习等新型数学与算法工具三方面的并行发展与无缝结合。光电器件、计算机与微处理器的计算性能仍然会在接下来的若干年内借助于“摩尔定律”的惯性（尽管并非严格遵守）持续增长。而正在孕育中的新型光学器件、光场调控机制、高性能图像传感器、数学算法与工具、并行/云/光/量子计算、人工智能技术必将为计算成像技术的未来发展注入新的活力。如今，计算光学成像已发展为一门集信息光学、计算机视觉、计算光学、现代信号处理、几何光学等理论于一体的新兴交叉技术研究领域。

这里值得提及的是，“成像中的计算”与“计算成像”有着本质的不同。计算成像虽然被称为“计算”成像，但其核心仍在于前端（物理域）的光学调控机制与成像系统表征，其从根本上决定了后端（数字域）信息处理技术所能解译与反演的信息量。简言之，如果成像系统前端所获取的原始信号（大部分情况是强度信息）的正向模型不明确或者数据不理想，仅依靠后端图像处理技术很难加以弥补。因为信息并不会凭空产生（这对当下非常流行的深度学习技术也适用），正所谓“巧妇难为无米之炊”[8]。因此，通过将前端（物理域）的光学调控与后端（数字域）信息处理的有机结合，计算光学成像对照明、成像系统进行光学编码与数学建模，以计算重构的方式获取图像与信息。这种新型的成像方式将有望突破传统光学成像技术对光学系统以及探测器制造工艺、工作条件、功耗成本等因素的限制，使其在功能（相位、光谱、偏振、光场、相干度、折射率、三维形貌、景深延拓，模糊复原，数字重聚焦，改变观测视角）、性能（空间分辨、时间分辨、光谱分辨、信息维度与探测灵敏度）、可靠性、可维护性等方面获得显著提高。正如本文的标题所示，这里所着重探讨的主题是光学成像系统的分辨率、超分辨率与空间带宽积拓展，这显然是计算光学成像技术所重点涉及的范畴。

另一方面我们不得不承认，由于缺乏系统性的理论体系与框架支撑，现阶段的计算光学成像并不能被称为一门系统性的光学分支学科。更准确地说，它可以被认为是一种对各类新兴光学成像机理“后知后觉”地总结归纳与抽象概括，并为人们提供了一个“包罗万象”的通用框架。例如，分辨率提升、超分辨率与空间带宽积拓展技术相关的研究可以追溯到20世纪中叶（例如合成孔径雷达，CT等技术），其历史甚至早于人类第一个数字-光学成像系统——电荷耦合器件（CCD）相机的发明（20世纪70年代中叶）。而超分辨成像技术，特别是荧光超分辨显微成像技术基于结构光照明、受激发射损耗[11]与荧光分子的光开关效应[12-14]等新颖光学调控机制，光学显微镜的衍射极限已被大幅突破，使光学显微镜的分辨率达到了纳米尺度。2014年，诺贝尔化学奖分别授予Eric Betzig, Stefan W. Hell 以及William E. Moerner三位科学家，以表彰他们在超分辨荧光显微成像技术方面的重大贡献。显然上述光学成像技术所取得的巨大成就是独立于 “计算成像” 领域所取得的。它们都源于本身所处于的学科方向，在实践中逐渐发展且逐渐形成了独具特色的系统理论与技术体系。但不可否认的是，这种基于个案（case-by-case）的研究方式难以揭示那些看似独立的成像方法之间的本质物理机理和内在关联。

本文标题的后半部分“从计算光学成像角度的一些思考”恰好阐明了本文的核心立场——通过将这些新型光学成像的具体个案置入“计算光学成像”这个更高维度的体系框架去分析与探讨，有望更深入系统地解释这些成像技术背后的物理学与光信息学本质，这将有望为设计和探索面向各类复杂现实成像应用的新型成像机理与方法提供有益的启示。值得说明的是，本文与我们不久前在《红外与激光工程》中所发表的综述“计算光学成像：何来，何处，何去，何从？”[8]侧重点有所区别。它并不力求面面俱到，而旨在反映一个核心思想——大多数提升分辨率，或者说“超分辨”及拓展空间带宽积的计算光学成像方法，它们本质上只是在若干物理机制的限制下，在“得”与“失”之间做出符合规律的权衡与选择，或者形象地说——"戴着脚镣跳舞"。这也从侧面印证了，在没有足够恰当的动机和缘由的情况下，滥用“超分辨”一词是存在一定隐患的。因为其忽略了在提高成像分辨率过程不可避免的基本“权衡”以及所需要付出的“代价”。

基于上述认识，本文“分辨率、超分辨率与空间带宽积拓展——从计算光学成像角度的一些思考”，概括性地介绍了分辨率、超分辨率与空间带宽积的相关基础理论，核心机理及其在计算光学成像中的若干实例。在第一章到第三章中，首先简要介绍分辨率与空间带宽积的基本概念与背景知识。对于一个成像系统而言，分辨率主要受限于光学系统衍射与探测器离散采样两方面。前者称为光学分辨率，受衍射极限影响；后者称为图像分辨率，受采样极限影响；二者共同决定了成像系统的解析力。而空间带宽积主要取决于成像系统的自由度，其可在相空间中简洁明了地可视化。第四章至第七章中，以Lukosz的超分辨原则[15-16]与Papoulis广义抽样[17-18]理论为出发点，阐述大部分提高成像分辨率的计算成像方法从本质上都可以被理解为一种 “空间带宽积调控”策略，即利用成像系统的可用自由度，在成像系统有限空间带宽积的限制下，以最佳方式进行编解码和传递信息的过程，并基于此分类对典型的超分辨率与空间带宽积扩展的计算成像方法进行了概述。最后，在第八章中针对若干未来重要的发展方向进行展望，并给出了本文的总结性评论。

2 光学分辨率与衍射极限

图像的空间分辨率是对图像细节分辨能力的衡量，是评价成像系统图像质量的关键指标，也是成像系统实际应用中应考虑的一个关键参数。成像系统的分辨率主要包括光学分辨率（衍射极限）与图像分辨率（像素尺寸）。二者共同成为光学成像系统空间分辨率的两大制约因素。光学分辨率本质上与光学系统的孔径大小以及用于观察样本标本的光波长有关。在表征光学分辨率时，通常需要考虑三个数学概念：‘艾里斑’、‘瑞利判据’、‘阿贝衍射极限’，它们分别从不同的角度衡量成像系统的分辨能力。以下按历史时间顺序逐一对这些术语进行解释。

2.1 空域单点准则——艾里斑（1835）

对于一个理想光学系统来说，一个无穷小的点物经过光学系统后，仍然会在像面汇聚为一个理想点。然而，在实际成像系统中，由于光的衍射现象，通过光学系统的点状物体最终会被成像为一个点状光斑，称为“艾里斑”。“艾里斑”是由英国数学家和天文学家G. B. Airy得名而来的。1835年，他在剑桥哲学学会学报上发表了一篇题为《有关圆孔径物镜的衍射》的论文[19]。论文以一个天文学家的视角描述了通过一个精良的望远镜观察到的恒星周围的光环或者射线的形状及亮度。尽管该文章是从天文学的角度去阐述的结论，但该结论对其他光学系统，特别是显微镜具有普适意义。图1为艾里斑的典型现象。如图1所示，艾里斑（Airy Disc）是在衍射限制的系统中由圆形孔径形成的聚焦的光点，其呈现为中央为亮点、周围是明暗相间的同心环。衍射图案由光的波长和光所通过的孔径大小决定。艾里斑的中心点含有大约83.8%的光强，第一个光强过零点出现在的位置如式(1)所示：

图1 艾里斑的典型现象，由其中心的最亮光点和环绕的衍射环组成Fig. 1 The typical phenomenon of an Airy spot consists of the brightest spot at its center and the surrounding diffraction ring

其中：λ表示波长，F# 为 成像系统的F数，NA为成像系统的数值孔径，其余16%的光强分布于环绕该点的衍射图案中。

“艾里斑”基于空域单点准则来衡量成像系统的分辨能力，它说明对于一个理想物点，即使采用一个没有像差的完善的透镜或光学系统成像，也得不到理想的几何像点，而仅能得到一个由孔径与波长决定的衍射光斑，这正是光学衍射与有限孔径效应的影响。光学分辨率与光学系统孔径成正比，与照明光源波长成反比，增加光学孔径，或者采用波长较短的光照明，都可提高分辨率。然而，艾里斑是从空域单点强度成像特性来衡量成像系统分辨能力的准则，其又被称为（光强）点扩散函数，通常用于描述非相干成像系统的成像特性。当然，实际成像中通常物体并不是一个理想点，而是可以看作无限密集的点目标的集合，成像系统观察时图像也是由许多光点组合而成的。因此，相比较采用单个光点的“艾里斑”准则，采用两点分辨能力的“瑞利判据”或许是更妥当的方式。

2.2 空域两点准则——“瑞利判据”（1896）

Rayleigh以Airy的理论为基础进一步延伸，于1896年创造了“瑞利判据”理论（Rayleigh Criterion）[20]。瑞利判据在衍射极限系统当中定义了分辨率极限，换言之，就是何时能够将2个光点相互区分或分辨开。如图2（彩图见期刊电子版）所示，当两个物点相距较远时，两个像斑也相距较远，此时两个物点可以被分辨，若两个物点相距很近，使得两个像斑重叠而混为一体，此时两个物点就不能再分辨了。瑞利提出了这样一个距离分辨标准 δRayleigh：当一个艾里斑的边缘与另一个艾里斑的中心恰好重合时，此时对应的两个物点刚好能被人眼或光学仪器所分辨，这个判据称为瑞利判据，用公式表示即：

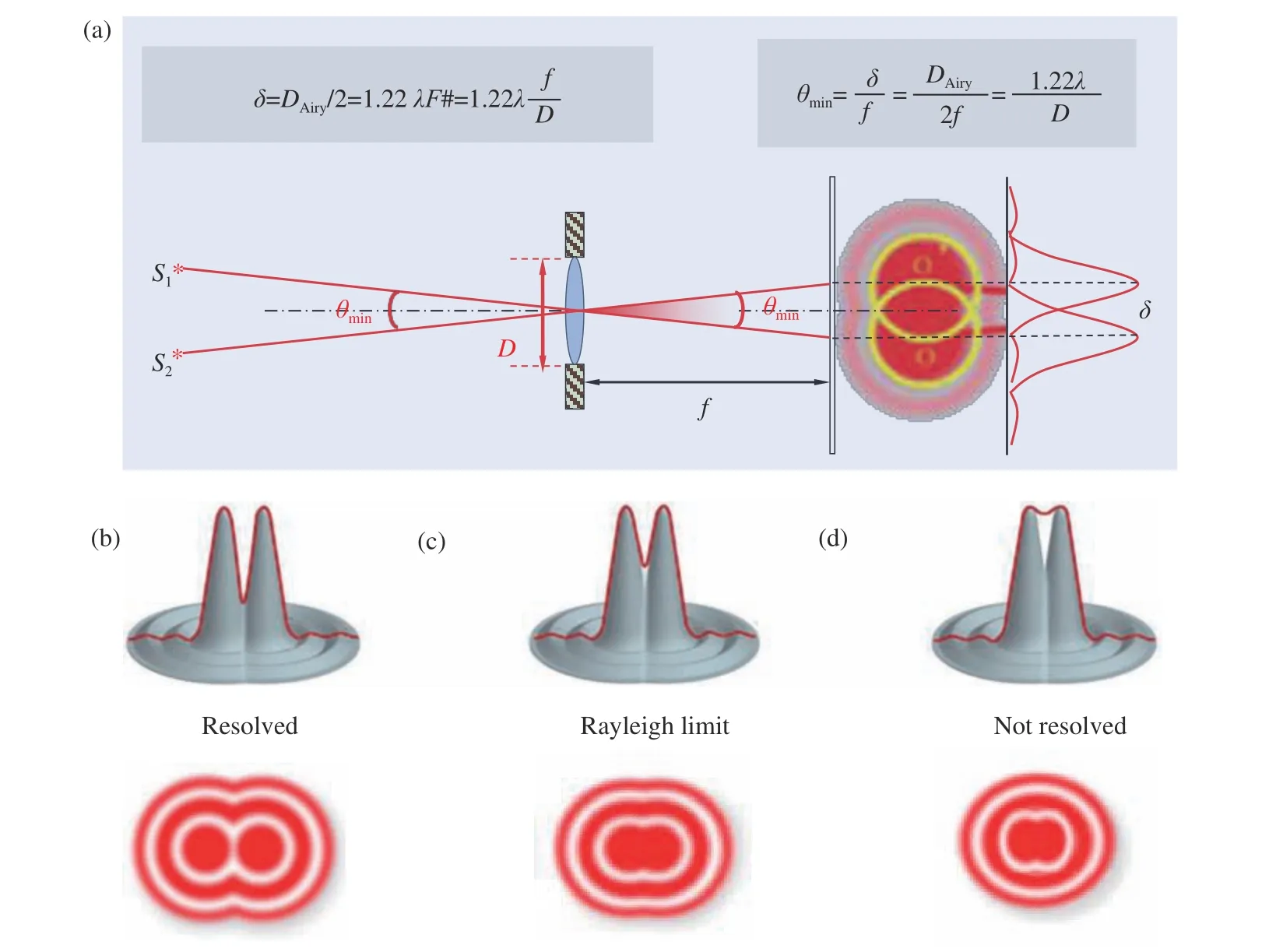
图2 “瑞利判据”的可视化表达。(a) 成像系统最小可分辨距离（光学角分辨率）与成像系统的孔径成反比。(b-d) 两个非相干的点目标在不同间距下所能拍摄到的艾里斑图像Fig. 2 Visual representation of the "Rayleigh criterion". (a) The minimum resolvable distance (optical angular resolution) of the imaging system is inversely proportional to the aperture of the imaging system. (b-d) Airy spot images of two noncoherent point targets at different spacings

假设两个艾里斑的峰值强度为1，中心凹陷位置的强度为0.735。根据瑞利判据，两个恰好能够分辨的衍射焦斑的明暗对比度的极限值是0.153。Rayleigh选择的标准是基于人类的视觉系统，并为观察者提供足够的对比度，以区分图像中的两个独立物点。值得说明的是，瑞利判据严格意义上并不是一个基本的物理定律，而是一个有些主观定义的值，这一点由其本人在1879年的论文中明确指出[21]。当满足瑞利判据，即当两个物点刚能分辨时，其对透镜中心的张角为最小分辨角：

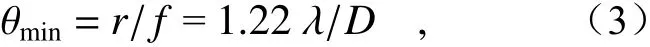
其中D为光学系统的口径，f为光学系统的焦距，它正好与艾里斑对透镜中心的张角相等。即对某种光学系统而言，一个物点通过其成的像斑越小，其分辨率才越高。正如之前所述，鉴于“分辨率”本身的含义就存在主观性与不确定性，瑞利判据因其简单方便而被人们广泛采纳，已经成为衡量光学系统分辨率的最普遍的定义之一。

2.3 频域线对准则——“阿贝衍射极限”（1873）

“阿贝衍射极限”是由德国数学家和物理学家E. K. Abbe而得名[22]。他与Carl Zeiss共同创立了“蔡司光学工作室”，即现在的蔡司公司，对光学显微镜的设计和理论做出了开创性的贡献。除此之外，Abbe还是定义数值孔径这一术语的首位学者：

式中n为 成像介质的折射率，α是物镜孔径角的一半。当成像介质为空气（折射率n=1），则数值孔径仅取决于所述孔径角的最大值（90°），即NA=sin90o=1。这是空气作为成像介质数值孔径（使用“干”显微物镜）的理论最大值。想要使数值孔径突破1，必须提升成像介质的折射率，如采用水（折射率1.33），甘油（折射率1.47）和浸油（折射率1.51）等。

1873年，Abbe发表了他关于显微镜图像生成的开创性论文“Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung”（对显微镜理论和显微视觉性质的贡献）[22]，提出了自己对光学成像系统原理的理解[22]：物是一系列具有不同空间频率二维光栅的集合，入射光经物平面发生夫琅和费衍射，在透镜焦面（频谱面）上形成一系列衍射光斑，各衍射光斑发出的球面次波在像面上相干叠加，从而形成图像，如图3（彩图见期刊电子版）所示。这就是著名的阿贝成像原理，其显式地将成像过程分为两步：分频与合成。而其中成像系统对分辨率的限制作用就体现在频谱面的低通滤波效应：物体包含从低频到高频的信息，透镜口径限制了高频信息通过，只许一定的低频信息通过，高频信息不能参与成像。因此，丢失了高频信息的光束再合成导致图像细节模糊。对于非相干成像系统而言，这个低通滤波器的截止频率为：

图3 阿贝成像原理显式将成像过程分为两步：分频与合成Fig. 3 The Abbe imaging principle explicitly divides the imaging process into two steps: frequency division and synthesis

其所对应的空域光栅线对的最小可分辨间距为

阿贝成像原理的意义在于：它基于傅立叶分析的理论来描述成像系统的成像过程，构成了傅立叶光学中成像系统分析的基石，也启发人们通过改造频谱的方法来进行光信息的调控与处理。

2.4 对光学衍射极限准则的探讨——常数游戏?

注意由阿贝成像原理所定义的“阿贝衍射极限”相比较瑞利判据而言系数上有些差异（常数系数为0.5而非0.61），这个值几乎对应于点扩散函数的半高宽（Full Width at Half Maximum, FWHM）。

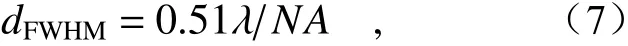
这背后有两方面因素：一是阿贝衍射极限是以周期光栅线对间距，而非两点间距作为分辨率判别准则的。尽管光栅线对间距也表示空间距离，但其本质上还是空间频率的等效表达，这与基于空域两点准则的瑞利判据从本质上是有所区别的。而且其最小可分辨间距衡量的是低通滤波器的截止频率（滤波器频域支持域，也就是非零的边界），这忽略了对比度的限制，因此是一种非常理想的情况。而瑞利判据中定义两点可分辨的明暗对比度的极限值是 0.153，这显然要比阿贝衍射极限更加苛刻一些，从而最小可分辨距离的值也就更大一些。值得提及的，如果将此对比度进一步从0.153放宽到极限值0，也就是两个艾里斑恰好完全重合成为一个平顶包络时，此时的两点分辨率判据称为斯派罗判据（Sparrow Criterion）[23]，可表示为

这个值更接近于从“阿贝衍射极限”公式中得到的最小可分辨线对间距（式(6)）。图4（彩图见期刊电子版）用一个实例给出了这些不同方法所得的分辨率判据的计算方法与差异。当使用510 nm的绿光及NA为1.4的油浸物镜时，基于瑞利判据的分辨率极限为222 nm，基于斯派罗判据的分辨率极限为171 nm，基于阿贝衍射极限判据的分辨率极限为182 nm，基于半高宽的分辨率极限为186 nm。

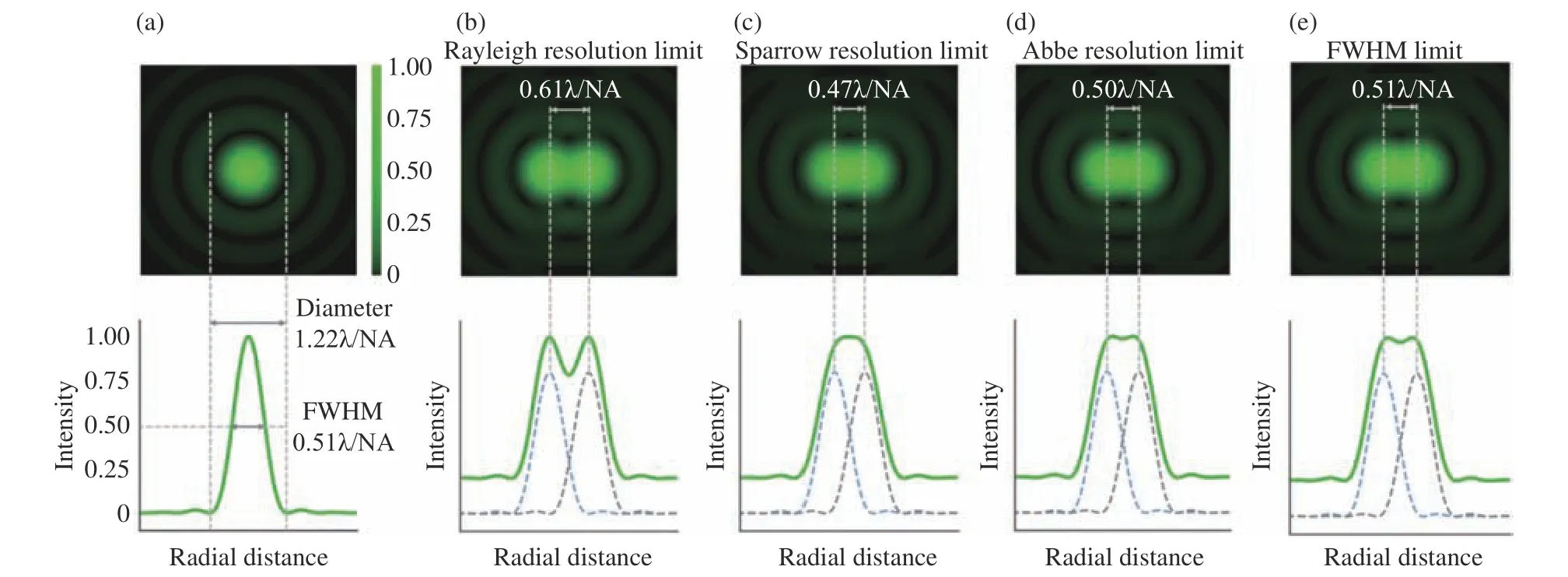
图4 艾里斑(a)与4个常用的分辨率度量准则（即Rayleigh (b)、 Sparrow (c)、 Abbe (d)和FWHM (e)）。灰色和蓝色的曲线代表试样中不同点的单个强度变化，其中垂直（y-）轴是强度，水平（x-）轴是各点之间的横向间隔。下图上方的曲线描述了所述的对强度分布的单独贡献，而下方的曲线展示了由各自上方曲线中的每个单独成分形成的叠加强度曲线Fig. 4 Airy spot (a) and 4 widely-utilized criterion (i.e., Rayleigh (b), Sparrow (c), Abbe (d), and FWHM (e)) for resolution computation. The gray and blue curves represent the individual intensity variations at different points in a specimen where the vertical (y-) axis is the intensity and the horizontal (x-) axis is the lateral separation between the points. The bottom plots describe the individual contributions to the intensity distribution while the top plots illustrate a super-imposed intensity profile formed by each of the individual components in the respective bottom plots

2.5 对光学分辨率的进一步探讨——传递函数理论与相干性

如前所述，从信息论的观点看来，光学系统传递的是随空间变化的图像。而光信息学，即信息光学，或傅立叶光学就是通信理论中傅立叶分析等一系列数学思想以及系统理论与光学（主要是波动光学）相结合的产物，其研究的是光信号表征、采集、分析、处理以及在自由空间与光学系统中传输的一般规律。J. W. Goodman的《傅立叶光学导论》[24]与《统计光学》[25]是这个领域最为重要的著作。它们分别利用傅立叶分析与概率统计的数学工具对不同相干态的光进行表述，并深刻揭示了它们干涉、衍射、偏振及成像等光学现象的本质规律。

从空域来看，任何载有物体或者场景信息的复杂光场信号，在空间域都可以看作不同统计特性（关联性）的点源（球面波）的组合；从频域来看，该复杂光场信号又可以看作各种空间频率（角度）的正/余弦或复指数函数（平面波）的集合（角谱）。光学系统（当然也包括自由空间）对输入的物空间的响应程度是通过空域点扩散函数来度量的，而光学系统对输入的物空间频率响应程度是通过频域的光学传递函数（OTF）来度量的，二者互为傅立叶变换。因此，一个光学成像系统的性能可直观且定量地通过光学传递函数（或等价点扩散函数）来体现。这种空间域与频率域的分析方式为分析成像系统的衍射极限提供了相互联系又有所区别的独特视角。

在本小节中，我们将目光从点扩散函数转向光学传递函数，因为基于空间频率域的光学传递函数理论不仅能给出分辨率的极限值，还能够更直观地给出目标不同空间频率信息的对比度传递值，因此逐渐成为评价光学成像系统像质的主要方法

OTF完全表征了系统的成像特性，即反映系统对不同空间频率正弦波分量的通过能力。其模通常称为调制传递函数或对比传递函数MTF，它表示被成像系统传递的不同空间频率成分调制度（或对比度）衰减的情况； O TF的相位由相位传递函数PTF表示，它表示被成像系统传递的空间频率在像面上相对其理想位置的偏移。如图5（彩图见期刊电子版）所示，OTF的作用在空域中等价于点扩散函数（PSF）和组成理想物函数各空间频率的卷积，该卷积效应会导致图像对比度的衰减（取决于MTF）或图像位置的偏移（取决于PTF）。值得注意的是，还可以将OTF利用欧拉公式展开：

图5 OTF 的幅值和相位成分。（a）表示 OTF 对强度调制的影响，即对比度的影响；（b）表示OTF对空间分布的影响。（c）OTF的大小完全取决于正弦波模式的最小强度（IMIN）与最大强度（IMAX）的相对大小。为了纳入可能的相移的影响，OTF是在复数坐标的单位圆内构建的，其实部和虚部反映了相移的大小，在这些坐标中，OTF 的实部和虚部的平方根给出，因此保持单位值，与相移无关Fig. 5 The magnitude and phase of the OTF. The former expresses the effect on intensity modulation, i.e., contrast (a), and the latter is the spatial distribution (b). OTF magnitude depends solely on the relative magnitude of the minimum intensity(IMIN) of the sinusoidal pattern vs. its maximum (IMAX). To incorporate the effect of a possible phase shift, OTF is constructed within a unit circle in complex coordinates, with its real and imaginary parts reflecting the magnitude of phase shift, but not the OTF magnitude itself, which is in these coordinates given by a square root of the sum of squared real and imaginary parts of OTF, therefore remaining unit value independent of the phase shift (c)

右边的两个因子分别为OTF的实部和虚部。前者是余弦函数，在空间频率为零时值为1，而后者为0。当PSF径向对称分布时（即光学系统与像差函数具有径向对称性，如散焦、球差的情况），其傅立叶变换的虚部为0。反之，当PSF径向非对称时，如成像系统存在彗差与像散时，OTF就会存在明显的虚部成分。

值得注意的是，之前所讨论的大多数结论都是针对非相干成像（如荧光显微成像、摄影、遥感等）的情形，而在许多光学成像与计量学应用中，通常需要引入主动照明照射待测样品：如高时空相干性的激光已成为传统干涉计量与全息成像等领域不可或缺的重要工具；而在众多新兴的计算成像领域（如计算光学显微成像），降低光源的相干性，即部分相干光源在获得高信噪比、高分辨率图像信息方面具有独特优越性[26-27]。因此，光学成像系统的传递函数理论与光场的相干性是密不可分的。这里由于篇幅所限，仅阐述最重要的结论部分：

对于相干成像系统而言，其为一个复振幅的线性系统，此时光学系统的传递函数被称作相干传递函数。对于一个没有像差的光学成像系统，其为一个理想的光瞳函数，即MTF在通带内恒为1，其截止频率为

因为理想的光瞳函数通常为只有0和1两个数值的低通滤波器（截止频率以内为1，截止频率以外为0），通带内的空间频率将被无衰减地通过，即成像系统具有很高的对比度。但是由于最终成像系统仅对光强信号敏感，所以往往只能探测到具有吸收成分的样品。当成像的物体具有一定的相位分布时，其复振幅分布可以近似为aeiϕ≈a(1+iϕ)，必须借助于传递函数的虚部成分才能够对相位信息成像[28-29]。如借助于基于阿贝空间滤波原理的相衬显微技术，或者在成像系统中引入光学像差，如离焦等的相位恢复与定量相位成像技术（如相干衍射成像[30-31]、光强传输方程[26,32]等），亦或是通过采用非对称照明或非对称孔径，以打破成像系统的径向对称性（如差分相衬显微成像[33-34]、傅立叶叠层显微成像[35-36]、四棱锥波前传感器[37-38]、或孔径分割/可编程显微成像[39-40]等）。

对非相干成像系统而言，其为一个光强的线性系统，此时光学系统的传递函数被称作非相干传递函数或光学传递函数。考虑到傅立叶自相关定理，光学传递函数是相干传递函数的归一化自相关，数学上可以通过两个移位的光瞳函数的积分得到，其截止频率被拓展到相干截止频率两倍，如图6（彩图见期刊电子版）所示。

图6 相干传递函数和非相干光学传递函数的计算模型和分布剖线Fig. 6 Computational model and distribution profile of coherent transfer function and optical transfer function under incoherence imaging condition

值得注意的是，由于非相干成像物面上各点的振幅和相位随时间变化的方式是彼此独立的，统计无关的。尽管物面上的每一点通过系统之后仍能得到一个对应的复振幅分布，但是由于物面是非相干的，此时的复振幅分布无法再像相干情况下被直接叠加，而仅仅对强度叠加。因此，非相干成像系统无法对物体的相位信息进行探测。同样注意到，光学传递函数的幅值随空间频率的增大呈现衰减趋势，这意味着增大成像孔径在获得高分辨率的同时还会导致成像的高频细节的衬度降低。

对于部分相干（介于相干与非相干之间）照明下的成像系统而言，情况会更为复杂一些，其严格的传递函数理论是在20世纪50年代由Hopkins基于统计光学原理建立起来的，揭示了成像系统中物体与图像之间的关系是双线性的，它们在频域中的传递关系通过交叉传递系数（TCC）来表征[41]。然而TCC的高维特性（对于二维成像系统而言是个四维函数）给部分相干成像的运算分析与计算反演都带来了极大的不便。但幸运地是，当被测物满足一阶Born或Rytvo近似时，部分相干成像系统可以近似为一个线性系统[42]，物体的吸收与相位成分均可以由TCC线性部分（令其空间频率坐标的其中之一为0即可得到）的实部与虚部所表征，且该传递函数与光场的相干性密切相关[26,43]。其量化截止频率由照明数值孔径NAill与物镜的数值孔径NA共同决定（二者之比被定义为相干参数[26,43]）

其中在显微镜中，NAill通常由聚光镜的孔径角决定。对于吸收物体成像，物体衬度在低空间频率处（空间频率小于 (NA-NAill)/λ区间）没有衰减，超过此区间将会出现类似非相干成像系统传递函数那样的衰减情况，到(NA+NAill)/λ时，最终衰减为0，如图7（彩图见期刊电子版）所示。对于相位物体成像，基本结论与相干照明类似，同样需要引入光学离焦像差或非对称照明/探测，才能使传递函数产生虚部成分，从而在图像中能够探测到相位成分。

图7 不同照明条件下的光学传递函数几何示意图。（a）相干与非相干成像情况（光源孔径无穷小或大于等于物镜孔径）；（b）部分相干成像情况（光源孔径小于物镜孔径）Fig. 7 Geometric schematic of the optical transfer function under different illumination conditions. (a) Coherent and incoherent imaging cases (source aperture is infinitely small, or is greater than or equal to the objective aperture); (b) partially coherent imaging case (source aperture is smaller than the objective aperture)

2.6 传统成像系统中的光学分辨率限制

在此章节的最后需要提及的是，不论是相干成像、非相干成像还是部分相干成像，上节所提及的分辨率公式本质上都是建立在阿贝衍射极限的基础上的。它们都可以结合2.1～2.3节所提到的一些标准判据稍作修改，如在一些文献中，部分相干照明下的瑞利衍射极限被简单地定义为[44-45]：

值得注意的是，由于瑞利衍射极限的系数1.22是在非相干成像条件下得到的结论，直接将其加以推广显得并不是那么严谨。当照明的相干性较低时有NAill＞0.5NA，该推广的精度是可以接受的。但当照明相干性较高时，情况就变得复杂一些。由上节传递函数理论可知，此时不能简单地将非相干成像的结果直接迁移到部分相干成像的情况，而需要具体情况具体分析[46-47]。例如，相干照明下的瑞利衍射极限被定义为[48-50]：

这显然比直接推广的情况要好上不少（1.22λ/NA），这是因为虽然截止频率仅为非相干成像的一半，但相干成像的MTF在通带内没有像非相干成像那样的衰减，而这也间接补偿了其两点分辨能力的损失。类似地，相干照明下的斯派罗衍射极限被定义为[48-49,45]：

尽管上述工作已经充分考虑了相干成像衬度的影响，但不得不承认其仍然有一定的争议与缺陷。正如J. W. Goodman在《傅立叶光学导论》所指出的[24]：相干成像下的两点分辨能力还与它们之间的相位差有关。图8显示了相干成像下两点源强度与它们相位差之间的关系，当二者同相位时，强度无法被分辨；但二者相位差增加到π/2，二者强度中间出现了一个凹陷，图像强度分布与非相干点源的分布相同；当相位正交时（相位差为π），凹陷一直下降到了0点，从而两个光源强度就被完全“解析”出来。因此，不能单一从两点的强度图像来判断相干成像下的分辨率，更不能以相位正交特例来说明相干成像下分辨率优于非相干成像。此外，在许多计算成像技术中，图像分辨率还依赖于所选取的成像模型、重建算法、以及噪声与重建伪影等，这都需要对相干成像下的分辨率准则进行拓展与补充。如R. Horstmeyer等[51]主张采用西门子星分辨率靶标（Siemens star target）置于成像视场各个位置的强度与相位图像来综合衡量其相干成像系统的分辨能力，如图9所示。

图8 相干成像下两点源强度与它们相位差之间的关系。竖线表示两个点源的位置。其中ϕ是两个点源之间的相对相位[24]Fig. 8 The relationship between the intensity of two point sources under coherent imaging and their phase difference. The vertical lines indicate the positions of the two point sources, where ϕ is the relative phase between the two point sources[24]

图9 用西门子星的分辨率靶标衡量相干成像系统的分辨率（波长 400 nm，100× 0.8NA，像素大小1.3 μm，有泊松噪声）[51]。（a）理想目标图像； （b）视场中心成像效果；（c）视场边缘成像效果（存在像差）；（d）沿着（c）中圈出的一段图像振幅值，周期为533 nm。由于“暗”辐条内的噪声值（圈出的）超过了“亮”辐条内的值，因此不可能明确地声称分辨率为533 nm。（e）周期为550 nm的辐条被清晰分辨（所有辐条都通过了验证）Fig. 9 Simulated example of a resolution report with the Siemens star for a coherent imaging system (λ = 0.40 μm, 100×0.8 numerical aperture objective, pixel size = 1.3 μm, with Poisson noise)[50]. (a) Ideal target image. (b) Imaging effect of region in while box of (a). (c) Re-imaged target center after moving it to the edge of the sensor, where aberrations further limit effective resolution. (d) Plot of amplitude values along a segment of the blue circle in (c) at 533 nm spoke periodicity. As noisy values within ‘dark’ spokes (circled) exceed values within ‘bright’ spokes, it is not possible to unambiguously claim a resolution of 533 nm. (e) Similar plot along the red circle in (c), showing that spokes at a periodicity of 550 nm are unambiguously resolved (verified for all spokes)

虽然本节所涉及的分辨率极限的定义准则有所区别，但它们背后所蕴含的物理涵义是类似的：要提高成像系统的光学分辨率，标本必须使用波长更短的光来进行观察，或者提高光学系统的孔径大小（对于显微镜而言，包括照明的数值孔径与探测的数值孔径）。但不管怎么样提高，其数值孔径也是有限的，不可能把物体散射的所有光都收集到。即使能够造出一个接近理想的物镜，能收集到所有的远场散射光，这个分辨率也难以看到比波长一半小的物体的细节（约在200 nm左右）[52]，这也即是传统光学成像系统中的衍射极限限制，如图10（彩图见期刊电子版）。

图10 阿贝衍射极限—— 光学成像系统难以看清比波长一半小的物体的细节Fig. 10 Abbe diffraction limit—optical imaging systems have difficulty seeing details of objects smaller than half the wavelength

3 图像分辨率与采样定律

如前所述，对于任意的光学成像系统，其成像过程可以被表述为：光源发出的光照射样品，经光学系统衍射并在其后焦面被成像系统的孔径选通并滤波，最终在图像平面形成影像的过程。随着从光学成像时代到光电数字化成像时代的转变，图像需要通过图像传感器件进行数字化离散采样和记录。这一过程要求能够记录光学图像的完整信息，以应对后续的观察和处理。因此，光学分辨率不再是限制成像系统分辨率的唯一因素，它和光电探测器件的图像分辨率一起成为制约系统空间分辨率的两大因素。

3.1 光学图像的离散化与数字化记录

成像数字化过程意味着对光学图像进行离散化采样，以形成一系列矩阵分布的采样网格。在每个采样点上，局部区域内的辐照度被积分，并被图像传感器所记录。这一过程可以建模为样本分布与系统点扩散函数的卷积。进一步而言，图像强度在每个采样点被量化，以产生一个整数灰度值，如图11（彩图见期刊电子版）所示。此过程将光学信号转换为数字信号并记录，为光学成像后续的存储与处理提供了数据基础。图像分辨率是衡量数字图像代表光学系统记录的模拟图像的精细细节的程度，其核心参数在于构建和渲染数字图像时使用的像素尺寸和数目。在同等视场下，随着数字图像采样和量化期间获取的像素数量增加，图像的空间分辨率也随之增加。理想的数字采样过程能够完整地记录光学图像的全部信号，样本的重要信息将完好无损地被记录并再现。而如果数字化采样过程无法完整记录光学图像的信号，那么将会产生信息混叠。也就是说，即使样本的信号可以被光学系统很好地传递，但是传感器的记录过程导致部分信息混叠，无法呈现光学系统的所有信息。

图11 光学图像的离散化与数字化记录过程。（a）原始理想光学图像；（b）局部区域的离散采样图像；（c）图（a）红框区域的局部放大图；（d）对应区域的像素灰度数值Fig. 11 The process of discretization and digital recording of optical images. (a) Original ideal optical image; (b) local area discrete sampling image; (c) enlarged view of the area in the red box in (a); (d) pixel gray scale of the corresponding area

3.2 香农-奈奎斯特（Shannon-Nyquist）采样定理

香农-奈奎斯特采样定理指出在满足两个条件的情况下，均匀间隔的采样点可以无误差地重构出原始信号的连续分布[53]。第一，该函数必须是有限带宽的，这意味着它的傅立叶频谱在某个截止频率（称之为截止频率）以上的所有频率都是零。第二，采样间距必须满足Nyquist所提出的奈奎斯特采样定理：大于信号中最高频率分量fmax的两倍。以图12所示的简单一维正弦波信号为例，当采样间距恰好满足Nyquist采样频率2fmax可以采集到正确的信号周期变化，此时原信号频谱沿频域产生复制但不产生混叠；当采样间距小于Nyquist采样频率 2fmax时，采样点无法正确反应原周期信号，此时信号频谱将产生混叠。

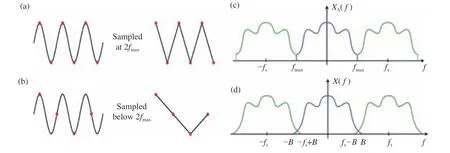
图12 香农-奈奎斯特采样定理。（a）采样间距恰好满足Nyquist采样频率 2 fmax可以采集到信号正确的周期变化；（b）采样间距小于Nyquist采样频率 2 fmax无法采集到正确的周期信号；（c）满足Nyquist采样频率时，原信号频谱沿频域产生复制但不产生混叠；（d）不满足Nyquist采样频率时信号频谱产生混叠Fig. 12 Shannon-Nyquist sampling theorem. (a) The correct periodic variation of the signal can be captured when the sampling spacing exactly satisfies the Nyquist sampling frequency 2 fmax; (b) the correct periodic signal cannot be captured when the sampling spacing is less than the Nyquist sampling frequency 2 fmax; (c) when the Nyquist sampling frequency is satisfied, the original signal spectrum is replicated along the frequency domain but no aliasing occurs; (d)the signal spectrum is overlapped when the Nyquist sampling frequency is not satisfied

将香农-奈奎斯特采样定理拓展到光学图像信号的离散采样可知，当探测器像素尺寸间距过大，或采样过于稀疏时，即不满足上述奈奎斯特采样定律时，将导致像素混叠效应。即探测器前光学图像的频谱中具有的高于Nyquist频率（采样频率的一半）的高频信息，会沿着Nyquist频率对折混入低频当中而不能被恢复。香农-奈奎斯特采样定理表明，成像系统的像质退化不仅发生在光学系统中，还发生在图像数字化的过程中——像素大小和间距都会造成像质的下降。整个系统的MTF是光学系统的MTF与传感器的MTF的乘积。首先，像素大小会造成对比度下降。因为一个像素的灰度值与它面积范围内光强的总和成正比，这类似于对原始连续光学图像利用均值滤波器做了一次卷积。其次，像素间距形成了离散采样，采样频率不足也可能会造成信息的丢失。如果假设Iin(x)为照射到探测器上的原始光学图像，探测器阵列的像元尺寸为p，像素间距为xd，探测器所拍摄到的离散信号可以被建模为[54]：

其中：⊗表示卷积。

从频域来看，该信号频谱是经过低通滤波的光学图像的频谱，即由宽度为1/p的sinc函数调制形成的低通滤波图像。采样相当于复制了图像的带限频谱的复制。

3.3 传统成像系统中的图像分辨率限制

光学图像的离散化与数字化记录过程最终导致的不良后果就是采样不足形成的“马赛克”效应，如图13所示。如果考虑到一个实际的光电成像系统，决定其探测距离的重要因素就是镜头焦距。当镜头焦距确定后，目标所成像的大小，也就是在焦平面上所占像素数与其距光学系统的距离有关。图13(c)给出了一个典型的红外热像仪对于人体目标在不同距离下的成像效果（像元尺寸为38 μm，像素分辨率为320×240，50 mm焦距镜头）。从图中可以看到，目标越远，其像所占用的像素点越少，“马赛克”效应越严重。正如约翰逊准则（Johnson Criteria）所定义的那样[55]，这种马赛克效应将成为限制搜索/跟踪系统的探测（目标所成的像在探测器焦平面上必须占到1.5个像素以上）、识别（目标所成的像在焦平面上必须占到6个像素以上）、以及辨认（目标所成的像在焦平面上必须占到12个像素以上）的关键瓶颈。

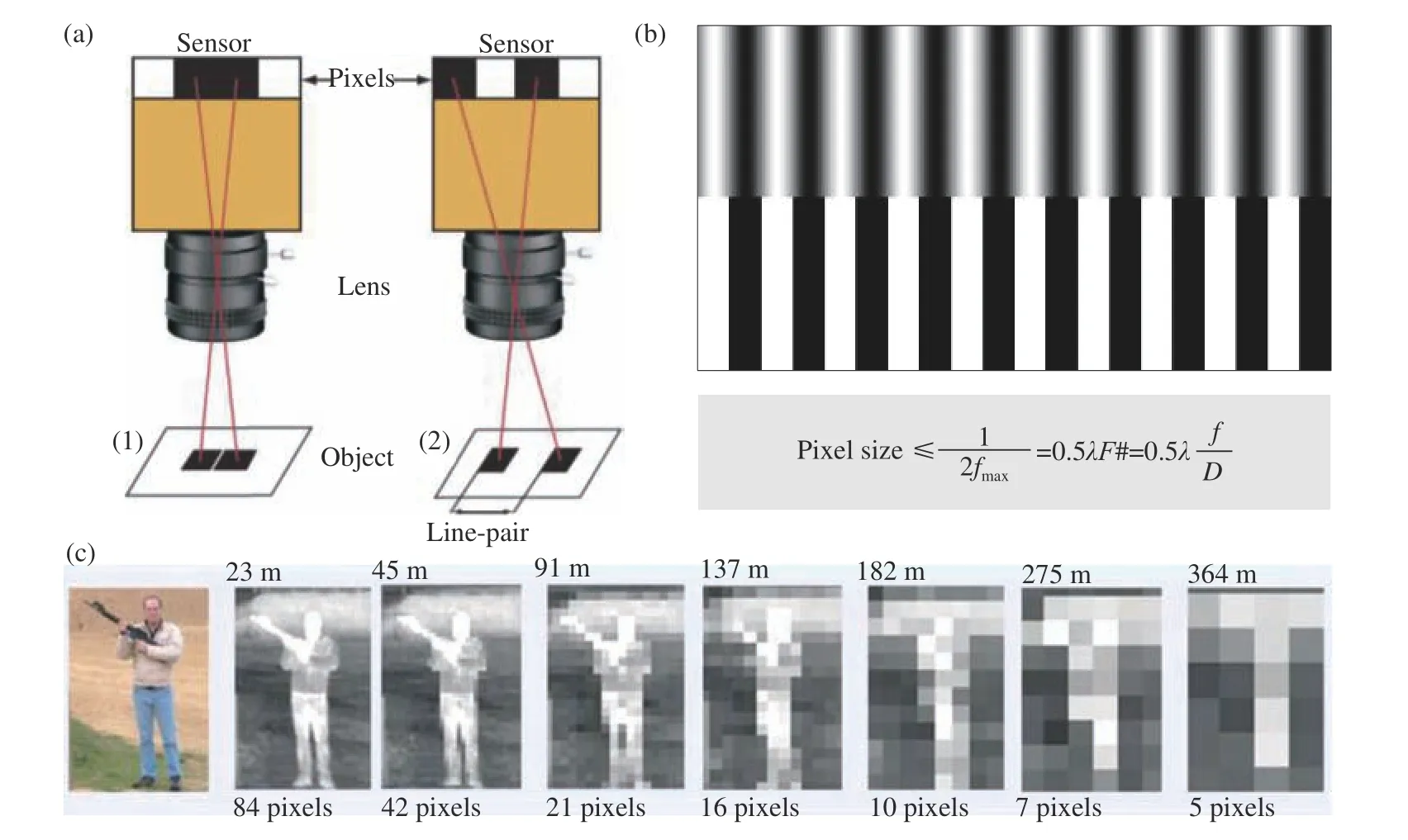
图13 探测器像元大小所限制的奈奎斯特采样极限（马赛克效应）。（a）像素采样不足（像素尺寸过大）所导致的信息混叠现象；（b）恰好满足奈奎斯特采样极限时的情况；（c）一个典型的红外热像仪对于人体目标在不同距离下的成像效果（像元尺寸为38 μm，像素为320×240，50 mm焦距镜头）Fig. 13 Nyquist sampling limit (mosaic effect) limited by detector image element size. (a) Information aliasing caused by under-sampling of pixels (too large pixel size); (b) The case when the Nyquist sampling limit is exactly satisfied; (c)imaging results of a typical thermal imaging camera for a human target at different distances (image element size of 38 μm, pixels of 320 × 240, and a lens of 50 mm focal length)

如前所述，提升图像分辨率的核心在于减小像元尺寸或增加像元数量。这种方式虽然看似简单直接，但实际实施时，通常面临以下4方面的问题：

（1）目前的探测器尺寸已经接近物理极限，受探测器工作条件和加工工艺的限制，通过减小像元尺寸和增加阵元数量的方式提高分辨率往往是十分困难的；特别对于某些特殊波段的探测器，如红外探测器，受制作工艺、工作条件、功耗成本等因素的限制，阵列规模仍然较小、像元尺寸较大，通常难以满足奈奎斯特采样定理[56]，无法完整记录光学图像的全部信号，从而难以满足对远距离弱小目标精准探测/识别所需要的成像分辨率的需求，如图14（彩图见期刊电子版）所示。

图14 大多数红外热像仪，如制冷中波热像仪和非制冷长波热像仪的像素尺寸较大。特别是当配备了在宽视场大口径的光学成像系统时，像元尺寸成为了限制其成像分辨率的根本因素（采样比Fλ/d小于2）[56]Fig. 14 The pixel size of most thermal imaging cameras,especially cooled mid-wave cameras and uncooled long-wave cameras, is large, especially when equipped with a large-aperture optical imaging system in a wide field of view, and the image element size becomes a fundamental factor limiting its imaging resolution (sampling ratio Fλ/d less than 2)[56]

（2）像元尺寸变小会导致光通量降低，灵敏度下降，产生严重的散粒噪声，后续补偿困难；

（3）高密度的探测器阵列会引入光电串扰问题，使得图像质量进一步恶化；

（4）信号通路增加将导致系统功耗、体积、重量、数据存储以及处理复杂度的增加。

值得说明的是，虽然本节侧重以远距离探测系统为例来说明，但是图像分辨率与采样在显微成像系统中也具有同等重要的作用。在显微成像系统中，必须谨慎地选择图像传感器件以对经光学系统放大的细节信息进行充分采样。然而，在采样要求更为严格的基于部分相干或非相干成像的光学系统中，采集到的原始图像经常会出现欠采样现象[57-60]。特别是针对大视场高分辨率的计算光学显微成像技术而言（如无透镜片上成像），这些原始欠采样的图像信息将导致成像分辨率出现严重损失。

4 图像信息量与空间带宽积

图像信息量与空间带宽积是光学成像系统信息论中的一个基础问题，其采用与评估一个通信系统类似的方式去评估一个成像系统的信息容量。在本节中将首先简要介绍光学系统信道容量问题的工具—光学信息论与相空间光学，然后再着重讨论图像的空间带宽积以及成像系统的空间带宽积限制。

4.1 光学成像系统的自由度

在香农信息论中的香农公式是通信领域最著名的公式之一，其描述了高斯白噪声干扰下连续信道的信道容量[61]：

式中，C代表信道，也就是传输通道可传送的最大信息速率，简称为信道容量；T为信号的传输时长；Δv为信号的传输带宽；S NR代表接收信号的信噪比；光学信息论通过将香农公式进行改良和拓展，以用于表征一个成像系统的光学信道容量。其中一个重要拓展是关于光学自由度的定义。在原始香农公式中的TΔv是时间信号以奈奎斯特采样率进行离散采样处理后的符号数。而单位符号能承载多少比特的信息，即比特数（类似于A/D过程中量化时的阶数）可以被理解为信号的自由度，也称系统的香农数。在光学成像系统中，被传递的图像信息由光场信号表征，其不再仅仅是时间的函数，因而需要重新考虑其自由度。本节所讨论的问题就是需要多少个独立变量来描述一个光信号。

光信号的自由度问题最早是由von Laue[62]（1914年）和后来的Gabor[63]（1961年）所提出的，他们把自由度解释为信息传递的通道。他们还认识到光学信号的自由度与几何光学的重要不变量，即史密斯-拉格朗日（Smith-Lagrange）不变量之间[64]的密切关系。而后，Toraldo di Francia在他1955年的论文[65]首次明确把自由度的概念引入光学领域，并借助于抽样定理得出了自由度的估计。考虑到成像系统孔径的限制，光信号以奈奎斯特采样率进行离散采样处理后的最高空间频率为Δv，且信号在空间域被包含在大小为D的窗口中，因此，可以估计描述信号的自由度，即描述一个光信号所需的独立变量的数量为

但因公式(19)没有考虑成像的多维特性与成像系统的时间带宽，因此是不完整的。将此定义扩展到具有有限的持续时间和时间带宽的二维光信号的情况，自由度的总数可以被定义为[66]：

其中Dx、Dy、Δvx和 Δvy表示图像x和y方向上的视场和空间带宽，而T和B指的是信号的时间长度和带宽。公式中3个常数“2”的前两个是用于标示当带限函数是复函数时，每一个采样值都由强度与相位两个自由度所决定，第三个常数“2”代表光场还有两个相互正交的偏振态。Toraldo di Francia的光学自由度显然并不十分严谨，1969年，他把Slepian、Pollak和Landau发展的回转椭球波函数[67-69]引入光学信息论，创立了光学本征理论，相干条件下无像差光学系统传递信息量的问题才得到了较为严谨的解读[67]。即便如此，由于光场实际上还有更多维度，如空间、时间、强度、相位、光谱、偏振、角动量、相干性等，其光学自由度数也应该是由这些维度叠加而来的[66,10]，所以这一表达也并不是最完整的。但上述公式至少反应了一个事实：可以为光场中每个独立的维度增加一个自由度，它们都能作为传输信息的载体。

4.2 相空间光学与维格纳（Wigner）分布函数

“相空间光学”（phase space optics）是一种对光场相干性进行度量与表征的一门系统学科分支，同时也是对成像系统承载信息能力进行定量分析的重要工具。不同于常见傅立叶变换的空间域或频率域，相空间光学是一个人为构造的多维空间，能够同时描述光信号的空间位置和空间频率（角谱）[70]。维格纳分布函数（Wigner Distribution Function，WDF）是最常用的相空间表达，其最早可追溯到1932年，Wigner[71]针对热力学体系的量子修正研究而提出一个描述粒子动力学状态的准概率分布函数。20世纪60年代，Dolin[72]和Walther[73-75]在辐射计量学领域中引入维格纳分布函数，并定义其为“广义辐亮度（generalized radiance）”。1979年，Bastiaans[76-83]正式将维格纳分布函数引入到傅立叶光学领域，系统地分析和总结了维格纳分布函数在光学成像与光信息处理中的应用，并论述了维格纳分布函数在描述部分相干光场的独特优势。由于维格纳分布函数能够同时表示信号的空间位置和空间频率特性，其既可满足对部分相干光场空域和频域信息关联特性的分析和处理的需求，又能够以近似光线的形式对部分相干光场分布的表征与传输进行直观的可视化[84]，从而搭建了波动光学和几何光学的桥梁，并为部分相干理论和成像系统分析提供了崭新的视角。

在经典部分相干理论中，互相干函数是描述部分相干光最常用的工具。然而它们的双线性的本质使其在计算中较为复杂，并且通常难以对公式背后所蕴含的物理意义做出直观解释。通过Wigner分布函数对部分相干光场进行表征能够有效克服上述缺点，简化对成像过程、系统以及相关机理的描述。对于部分相干光场U(x,t)，其中x=(x,y)为二维空间坐标，维格纳分布函数被定义为其交叉谱密度函数在差分变换坐标系下的傅立叶变换[70]：

其中u是 对应于x在 空间频率域的坐标,G(x1,x2)为光场的交叉谱密度函数。注意与交叉谱密度函数G(x1,x2)类似，维格纳分布函数等价描述了一个多色部分相干光场中单色成分的系综相关特性，即光场的空间相干性。

维格纳分布函数严格来说可以被理解为关于光子的位置和动能的概率密度分布。单色相干光波场的标量复振幅函数在某一个平面上的空间频率坐标实际上对应不同角度传播的平面波分量（角谱），所以可以将维格纳分布函数W(x,u)中的u近似地理解为某点x处的光线分布的角度。由于位置与方向（动能）是唯一确定一束光线的两个元素，维格纳分布函数又可以被理解为一种更加严格的光线模型，被定义为广义辐亮度：不同于传统辐亮度，广义辐亮度可以取负值[85]。它不仅考虑了光线的直线传播，还能够精确描述光波的波动光学效应，如干涉与衍射现象。当U(x)为单色相干光波场时，G(x1,x2)=U(x1)U*(x2)，则其维格纳分布函数可以表示为

如表1所示，维格纳分布函数具有空间边缘（spatial marginal）性质、频率边缘（spatial frequency marginal）性质、卷积（convolution）和瞬时频率（instantaneous frequency）等重要性质。维格纳分布函数具有空间、频率双重表述功能，其空间传播与光学变换性质却无一例外地遵循光线模型。这使维格纳分布函数成为一座连接几何光学（光度学）与物理光学的桥梁，为成像系统分析和光信号处理提供了一种非常简单而实用的工具。表2为维格纳分布函数的常见光学变换，它们在相空间所对应的维格纳分布函数的变化作用总结于图15。

图15 常见信号变换在相空间的表征。（a）菲涅耳传播；（b）Chirp调制（透镜）；（c）傅立叶变换；（d）分数阶傅立叶变换；（e）光束放大器Fig. 15 The characterization of common signal transformations in phase space. (a) Fresnel propagation; (b) Chirp modulation(lens); (c) Fourier transform; (d) Fractional Fourier transform; (e) beam magnifier

表1 维格纳分布函数的性质Tab. 1 Properties of WDF

表2 维格纳分布函数的常见光学变换Tab. 2 Common optical transformations of WDF

4.3 空 间 带 宽 积（Space-Bandwidth Product，SBP）与相空间图（Phase Space Diagram，PSD）

空间带宽积一方面可以用来度量成像系统的信息量，另一方面，对于记录系统来说，也可以衡量系统接收信息量的能力，具体到成像系统中，可以用来衡量成像系统可以测量物体的大小和细节分辨的能力。为简单化，本小节仅考虑成像系统空间坐标一维的情况，此时空间带宽积同式(19)，N=DΔv， 此时，D代表物体所占据的空间域成像视场，Δv为物体满足奈奎斯特采样定律下的信号带宽。不难发现，此定义与Toraldo di Francia所描述的光信号的自由度一致[65]，其等效于有效视场和系统截止频率所确定的通带面积的乘积。SBP是评价系统性能的重要参数，既可以描述图像的信息容量，又可用来描述系统的信息传递和处理能力。结合上一小节相空间光学与维格纳分布函数的定义可以发现，上述空间带宽积可以直观地用它在相空间，即空间-频域中所覆盖的面积来描述。维格纳函数分布中支持域（非0区域）所围成的面积便是空间带宽积，因此维格纳函数可以视为系统空间带宽积的一种全面的度量工具，它不仅给出了空间带宽积的值，也给出了空间带宽的分布情况。将这种相空间下描述空间带宽积的可视化表达方式称作相空间图或维格纳图[86,70]。

图15所示的即是一个在空间域与频率域都为有限支持域的信号在不同光学变换下的PSD，当光场经菲涅尔衍射后，维格纳分布函数产生了水平方向的剪切（图15(a)），当光信号通过一个理想的薄透镜时，啁啾信号调制下（即信号与二次相位函数的乘法）的维格纳分布函数产生了垂直方向的剪切（图15(b)）；光信号通过傅立叶透镜，或对信号进行远场衍射，傅立叶变换作用引起维格纳分布函数90°旋转（图15(c)）等。所有这些对维格纳分布函数产生的变换都是线性正则变换（Linear Canonical Transform，LCT）的特例[70,87]。它们将其每个x-u坐标映射到一个新的位置，且该坐标映射是仿射的，也就是说PSD内部阴影区域的面积在映射前后是保持不变的，这形象地说明了线性正则变换下光学成像系统的有限空间带宽积应与信息量守恒，也就是说其SBP是一个定值，这类似于海森堡不确定性原理。值得一提的是，早在1914年，von Laue就从光学信息论的角度指出了光学系统信息量守恒原理：给定一个光学系统，它能传递的光信息自由度数是常量，因为该系统可传递的空间频带是不变的[62]。但是von Laue支持该理论的理由却是错误的，直到1966年才由Lukosz纠正并建立了Laue-Lukosz自由度不变定理[15]：给定一个光学系统，其可传递的光信息自由度数是常量；系统的空间频带却是可变的，因为可以通过减少总自由度数N某一个因子来扩展空间频带宽，以提升成像系统的分辨率，该部分将在第5章详细讨论。

不难发现，当PSD保持长方形的形状时，对图像传感器的空间带宽积要求最低，此时PSD的面积正好等于在奈奎斯特极限下完整表示信号所需的采样样本数，即其有效可分辨像元的数目，更具体而言，其被定义为[88-90]

其中：r=λF#=0.5λ/NA，为成像系统在非相干成像条件下的阿贝衍射极限分辨率，F#代表镜头的F数，NA代表其对应的数值孔径，0.5这个因子是由于奈奎斯特采样定律所引入的。

4.4 传统成像系统中的空间带宽积限制

基于光学系统空间带宽积守恒原理，对于传统成像系统而言，通过镜头聚焦并被成像设备采集到的物体的信息量，也就是其空间带宽积总是有限的。如图16及表3所示，现有的成像镜头的空间带宽积都在千万像素量级（10 Megapixels），且随着镜头焦距的提高（角分辨率提高），成像系统的空间带宽积不但没有提升，反而有所下降[2,5-6]。这种有限的空间带宽积是制约广域监视、天文观测、航天遥感、边防预警等成像系统对复杂环境下的目标进行有效探测、识别与感知的关键瓶颈。

表3 典型35 mm单反相机镜头的空间带宽积Tab. 3 Spatial bandwidth product of typical 35 mm SLR lens

图16 对于传统光学系统，视场与分辨率这两个参数互相矛盾，无法同时兼顾。（a）35 mm单反相机不同焦距下所对应的视场角；（b）35 mm单反相机不同焦距下所拍摄到的典型图像Fig. 16 For conventional optical systems, the two parameters of the field of view and resolution are contradictory and cannot be accommodated at the same time. (a) Field of view of 35 mm SLR cameras at different focal lengths; (b) typical images captured by 35 mm SLR cameras at different focal lengths

成像视场与分辨率的矛盾同样存在于传统显微成像系统中。如图17所示，对于一个传统光学成像系统，空间分辨率的提高与视场的扩大往往是一对难以调和的矛盾[91]。如表4所示，随着物镜放大倍数的提高，成像视场直径呈反比线性缩小，但是光学分辨率极限却很难做到线性提升（放大率超过40倍时尤其明显），因此，传统显微成像系统始终受限于空间分辨率与视场大小之间的矛盾。目前，现有的大部分显微物镜的空间带宽积也在千万像素量级，这种有限的空间带宽积

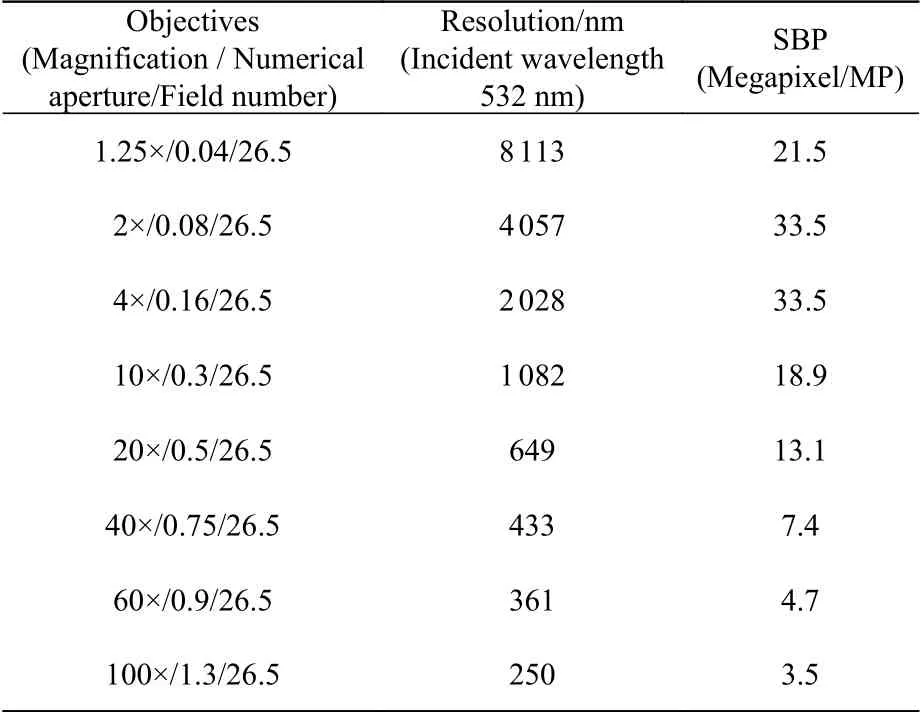
表4 典型的显微物镜的空间带宽积Tab. 4 Spatial bandwidth product of typical microscopic objectives

图17 传统显微镜存在分辨率与视场大小难以同时兼顾的矛盾：低倍镜下视野大，但分辨率低；切换到高倍镜后分辨率虽得以提升，视场却相应的成更高比例的缩减Fig. 17 There is a tradeoff between the resolution and FOV in traditional microscopes: the FOV under low-magnification objective is large with the low resolution; for high-magnification objective, the resolution is improved while the FOV is reduced dramatically

与宏观成像系统一样，成为制约显微成像系统应对复杂生物样品（如细胞集群）的单细胞研究的关键瓶颈[92]。虽然利用高倍物镜结合视场拼接技术可以同时实现高分辨与宽视野成像，达到提升空间带宽积的目的，但机械扫描与图像拼接降低了成像速度，致使成像系统的时空带宽积（Space-Time-Bandwidth Product，STBP，即单位时间内的SBP）降低，从而无法为单细胞分析提供研究细胞生命现象动态过程所需的高时间分辨率[93-94]。因此，如何有效突破成像系统的时空带宽积限制，实现高通量成像，是目前计算光学成像研究的一大重要方向。

5 （光学）超分辨成像——基于空间带宽积调控的视角

本节借助于Lukosz的超分辨原理来阐述大部分提高光学成像的光学分辨率的计算成像方法从本质上都可以被理解为一种“空间带宽积调控”（space-bandwidth product adaptation）策略。Lukosz在他的两篇开创性的论文中指出[15-16]，图像分辨率并不是单纯由其频域带宽决定的，而是由其总的空间带宽积决定的。因此可以借助于一定的编码方案，将总信道容量的一部分用于传输图像信号的各个频段，这些频段甚至可以在原系统的通带之外，从而为突破成像系统的分辨率衍射极限提供了可能性。当然为了满足空间带宽积的限制，所能成像的目标视场大小也必须相应进行缩放，以保持传输信号信息的总量守恒。

5.1 Lukosz空间带宽积调控

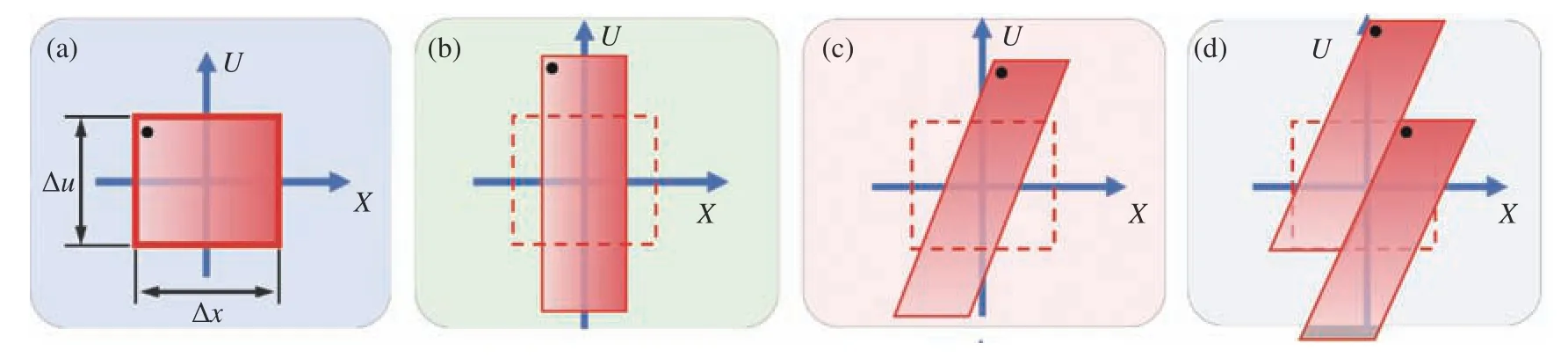
Lukosz所提出的“空间带宽积调控”本质上是利用成像系统的可用自由度，在成像系统有限空间带宽积的限制下，以最佳方式进行编解码和传递信息的过程[15-16]。图18展示了Lukosz在其原著中提出的成像系统，相干照明下的物体的波前传播到第一透镜前方的光栅上，光栅衍射产生物光场的两个副本，它们以不同但共轭的方向传播。4f系统将紧靠光栅G1后方的波前成像到共轭平面，第二个相同的光栅G2位于该平面上。Lukosz从原理上推导出通过该系统可将成像分辨率提升至孔径限制下衍射极限的两倍。该原理可以借助于PSD进行直观阐述[88-89,95]。如图19所示，根据上节中所定义的相空间中的SBP概念，考虑一个空间上紧凑，同时在频带上受限的信号，满足SBP=ΔxΔv。图19(a)显示了成像系统在没有光栅的情况下传输信号的PSD。为了在保持传输信号信息总量守恒的前提下将图像分辨率提高两倍，需要将其视场缩减到原来的一半（图19(b)）。在这种情况下，物光信号自由空间中傍轴衍射对应于信号相空间区域的水平剪切。传播到第一个光栅对应于一个水平剪切（图19(c)）。随后用光栅函数进行调制，将信号分成两个相同的副本，每个副本都沿频率轴移动（图19(d)）。透镜的傅立叶变换作用交换了相空间的空间轴和频率轴，使其在相空间中顺时针旋转了90°。而4f系统的有限孔径效应相当于抹去了由光学系统传输的频段之外的所有频率（图19(e)）。光场传播到达第二个光栅再次产生了两个相同的副本，每个副本沿频率轴向相反方向移动（图19(f)）。因此，获得了3个信号分量，其中中间完整的那个是所期待恢复的（但经过菲涅耳传播的）输入信号。因此，将信号反向传播到输出图像平面（图19(g)），并应用空间滤波器滤除掉不需要的信号分量或伪影（图19(h)），就可以恢复出原信号。

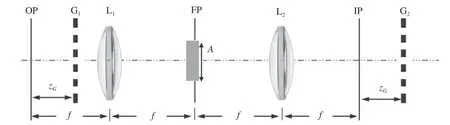
图18 Lukosz型超分辨率系统。物体平面（OP）的信号被传播到第一个光栅（G1）。然后，编码信号通过由两个傅立叶透镜L1和L2组成的4f成像系统成像到位于第二个光栅（G2）的共轭平面。系统孔径大小为A，位于夫琅禾夫平面（FP）。解码后的信号在系统的图像平面（IP）中被观察到Fig. 18 Lukosz-type superresolution system. The signal in the object plane (OP) is propagated to the first grating (G1). The encoded signal is then imaged to the conjugate plane located at the second grating (G2) by the 4f imaging system consisting of two Fourier lenses, L1 and L2. The system aperture of size A resides in the Fraunhofer plane (FP). The decoded signal is observed in the image plane (IP) of the system

图19 超分辨率系统的相空间图。（a）通过4f系统的信号，没有编码；（b）带宽超过4f系统通带2倍的信号；（c）第一个光栅（G1）之前；（d）G1之后；（e）通过4f系统后和第二个光栅（G2）之前的编码信号；（f）G2之后；（g）信号反传播到图像平面IP；（h）去除信号区域外的伪影之后Fig. 19 Phase-space diagram of the superresolution system. (a) Signal passing the 4f system without encoding; (b) signal with a bandwidth exceeding the pass band of the 4f system by a factor of two; (c) before the first grating (G1); (d) after G1;(e) encoded signal after passing the 4f system and before the second grating (G2); (f) after G2; (g) signal back-propagated to the image plane IP; and (h) after removing artifacts outside the signal area

5.2 提升分辨率所需要付出的成本与代价

虽然上节中所提及的Lukosz超分辨率系统已经在实验中得以成功验证[96]，但必须意识到实现超分辨是需要付出成本与代价的。首先，即使在理想的条件下，输出信号的能量也只有输入信号的四分之一。一般来说，信号功率的损失与分辨率提高的倍数成正比。成像系统的孔径和输出平面的空间滤波器都会将所接收信号的能量减半。这会导致成像信噪比的损失。更重要的是，如果将整个成像系统（包括衍射光栅）视为一个黑匣子，它其实只是一个分辨率为1 /2Δu的成像系统。但不可否认的是，它的内部清晰地包含了信息编码、信道传输以及信息解码几个部分（尽管信息解码部分是由光学系统完成的，但这不影响对其性质所作出的界定）。这就像一个典型的通信系统：信源信息通过信源编码、信道编码后，经过调制器加载到载波调制信号上通过信道进行传输。在信道的另一端，信号将先经过解调，再通过信道解码、信源解码后，送到信宿处。Lukosz超分辨率的思想反映的是计算光学成像的最精髓部分，即“先调制，再拍摄，最后解调”这种“混合光学—数字”成像方式的缩影。

相空间分析使我们能够明确看到Lukosz超分辨率方案的另一个非常重要的代价：编码步骤产生了PSD的复制与扩展，原始信号的两个副本在相空间需要合理安置以确保它们不相重叠（在相空间中是正交的），并且能够在孔径函数截断后重新组合。这个概念可以进一步扩展到同时考虑空间和时间等多维自由度的情况——即Laue-Lukosz自由度不变定理[97]：给定一个光学系统，其可传递的光信息自由度数是常量；但系统的空间频带却是可变的，因为可以通过调控自由度数N中某些因子来扩展空间频率带宽。例如采用时域编码和时频复合编码的方式扩展相空间，此时由于整个信息空间已经拓展到了由空间和空间频率坐标以及时间和时间频率组成的扩展相空间，传输信号在此扩展相空间中的正交性往往更容易得到满足[98-99]。另一方面，由于额外时间维度的引入，甚至依托于高维数据的冗余性放宽“相空间有部分重叠”这一限制性条件，而信号本身可以从具有重叠的多次测量值中反演重建出来。最终，Lukosz超分辨率方案也可以拓展到非相干成像与结构光场照明的场合，因为其PSD的剪切、复制、扩展、截断、重组等相空间操作都可以适用于任意相干态的光波场。上述思想在现阶段许多计算成像超分辨技术中都被体现的淋漓尽致，如分时合成孔径雷达、傅立叶叠层显微成像以及结构光照明超分辨显微术等。但无论如何，这些技术都脱离不了一个最基本的前提假设——信息不会无中生有，想要在“分辨率”上有所“得”，就必须在另一个光学自由度上，如时间分辨率、成像视场等，有所“失”。它们实质上都是在物理限制下，在“得”与“失”之间所作出的符合规律的权衡与选择。

5.3 （光学）超分辨成像的典型计算成像案例

Lukosz所提出的“空间带宽积调控”其实是一种内涵广泛且具有普适意义的超分辨成像思想，但在当时由于基于“调制解调”的计算成像思想仅仅处于启蒙阶段，在他关于超分辨率的开创性论文中仅给出了非常有限的实例来支撑他的思想[15-16]。而如今，计算光学成像已全面进入了“百花齐放，百家争鸣”的繁荣发展局面，现在已经有大量成熟的样例来充分体现Lukosz超分辨成像思想。基于 Laue-Lukosz 自由度不变定理，可以看出经典空间频带展宽可通过牺牲另一个维度上的自由度来实现，如以牺牲时间分辨换取空间分辨的合成孔径、结构光照明技术以及牺牲视场的点扩散函数工程的超分辨成像技术等。

5.3.1 合成孔径

光学衍射极限对系统成像分辨能力的限制本质上是系统孔径的限制，即有限的系统孔径限制了成像系统的成像分辨能力。合成孔径光学超分辨率成像技术主要借助于Lukosz超分辨率思想，通过多个小口径光学系统的图像数据合成等效获得大口径光学系统的成像能力。传统合成孔径成像技术是一种基于主动照明的相干探测成像机制，如图20所示的合成孔径雷达（Synthetic Aperture Radar，SAR）或许是人类历史上最早采用“计算成像”思想的光电探测系统（尽管是在微波波段）[100]。通过发射大时宽-带宽积的信号（如线性调频信号），对目标回波进行脉冲压缩，获得面向距离的高分辨率；其成像原理是在平台与目标相对运动的情况下，利用多普勒频率的线性变化，记录平台不同位置处的目标回波信号；经过数据处理，将发射孔径在空间上合成一个虚拟大孔径，实现方位聚焦，获得方位向的高分辨率图像。

图20 最早的合成孔径“计算成像”技术——合成孔径雷达Fig. 20 Synthetic Aperture Radar (SAR), the earliest computational imaging technique

将合成孔径雷达的思想扩展到光学波段，形成了激光合成孔径雷达技术（Synthetic Aperture Ladar，SAL）[101]。2002年，美国空军实验室利用移动孔径和漫反射散射目标成功研制了世界上第一个真正的合成孔径激光雷达装置[102]。2005年，美国Aerospace公司同样采用1.5 μm波长的光纤激光器第一次实现了真正意义上的激光合成孔径雷达成像（如图21所示）：大小为5 mm×8 mm漫反射目标，在距离2 m处进行合成孔径成像[103]。类似于SAR，基于激光合成孔径的SAL也是以提升有效成像孔径为目标的[104-105]，但SAL的激光发射孔径衍射极限与SAR的天线束宽相比要小得多[106-107]。并且其合成孔径长度远小于传统SAR的合成孔径长度，即相同时间内需要处理的数据量没有SAR那么大，这也就加快了战场情报的掌握速度。此外相比于SAR，SAL工作在光学波段，它的高分辨率和对微小表面的成像能力，以及这些图像看起来更自然、更容易理解的事实，对于快速掌握战场环境细节非常适合。

图21 激光合成孔径雷达技术[102]。（a）美国Aerospace公司研制的基于光纤的激光合成孔径雷达成像原理图；（b）成像结果对比（右图为衍射受限成像结果，左图为合成孔径后的结果图）Fig. 21 Synthetic Aperture Ladar (SAR)[102]. (a) Principle diagram of laser synthetic aperture radar imaging based on optical fibers developed by Aerospace Corporation of the United States; (b) comparison of imaging results (right image is diffraction-limited imaging results, left image is synthetic aperture results)

不管是微波波段还是光学波段的合成孔径雷达技术，都基于相干探测原理，如干涉测量或全息的方法记录复数振幅。但值得一提的是，合成孔径技术其实并不依赖于相干测量与相位直接探测。2013年，Zheng等[35]提出了傅立叶叠层显微成像（Fourier Ptychographic Microscopy，FPM）技术：样品被不同角度的照明光束（通常是一个LED阵列）依次照射（见图22），采集的低分辨率图像在频域基于叠层相位恢复算法实现合成孔径，从而使频谱支持域得到显著提升[108-110]。与传统的合成孔径超分辨率算法不同，相位恢复和频域合成孔径在傅立叶叠加成像重叠更新算法中同时完成，这就是傅立叶叠层成像技术本身的魅力所在。通常情况下，傅立叶叠层成像技术使用低倍率物镜的低数值孔径来获得大视野，然后使用大角度范围的照明光束在频域中依次照亮样品来合成孔径。最终图像的等效数值孔径提高到物镜和照明的数值孔径之和，同时保持低倍率物镜的大视场，从而实现大空间带宽积。

图22 傅立叶叠层显微成像技术原理图Fig. 22 Schematic diagram of Fourier ptychographic microscopy

2016年，Holloway等[111]首次将傅立叶叠层成像技术应用在远距离成像中，通过频域中的孔径交叠反复迭代投影更新并恢复目标不同的空间频率的振幅与相位成分，在非干涉条件下以单次曝光实现合成孔径主动超分辨率成像。该技术虽然采用相干激光照明，但并不采用干涉的方式对散射场的强度和相位进行直接探测。随后在2017年，Holloway等[112]又在之前的基础上对透射式系统进行改进，提出了反射光路结构的宏观傅立叶叠层成像系统，其系统结构如图23所示。在反射式系统中，通过对散斑噪声的处理而能够对漫反射物体进行测量，使该技术面向远距离目标探测的实用性更近了一步。

图23 反射式傅立叶叠层成像系统实物与原理图[111]Fig. 23 Reflective Fourier ptychographic imaging system and its schematic diagram[111]

上述相干合成孔径成像技术，都需要在照明光源具有极高相干性的条件下才能实现，因此不可避免地需要采取激光主动照明的方式。然而，针对远场目标探测的应用环境，主动激光照明对激光功率、发散角、稳定性等都提出了诸多具有挑战性的要求。尤其是在战场监测等应用环境下，主动照明还会引发自我暴露等问题，对其应用场景有一定限制。因此，研究在太阳光、月光等被动照明下的非相干合成孔径技术也必将是未来的一大发展趋势。但由于非相干成像条件下物场相位信息已经丢失，直接对其强度探测无法将其信息在频域进行有效融合，因此其核心问题是非相干条件下物场波前相位信息的获取。范西特-泽尼克定理表明非相干目标的光强分布与其远场互强度函数互为傅立叶变换。因此，只需在非相干光场的前提下实现相位复原与频谱填充，就可实现目标强度的合成孔径成像。如图24所示，非相干合成孔径反演成像基于多个分立子孔径对来自目标的各方向散射光进行收集，然后通过逐点关联干涉[113-114]、非相干全息[115]、傅立叶叠层[116]等相位测量或恢复技术计算各子孔径下的复振幅分布，然后通过分时合成填充大口径光学成像系统才能获得的物场频谱，进而利用傅立叶逆变换重建高分辨率的目标图像。

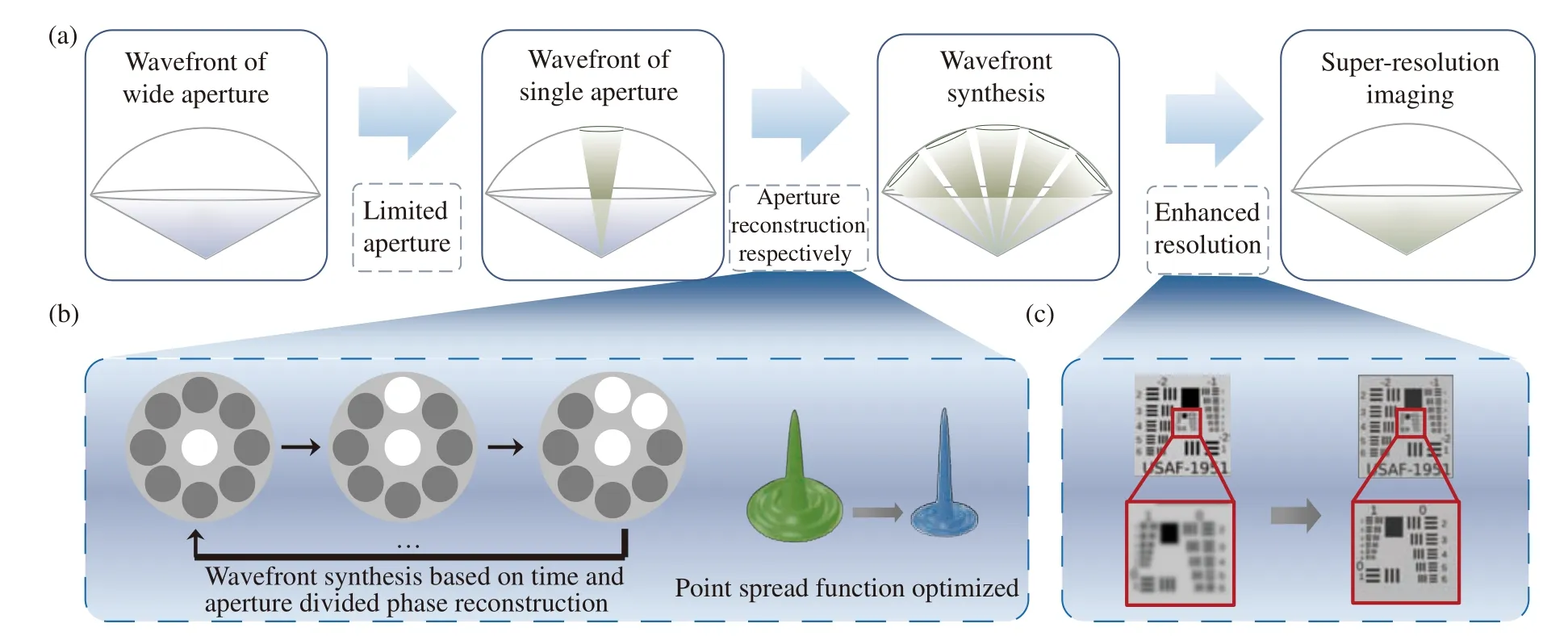
图24 非相干合成孔径技术原理[116]。（a）分时分孔径相位反演合成孔径过程；（b）基于分时分孔径相位反演合成孔径实现点扩散函数优化；（c）超分辨前后成像对比Fig. 24 Principle of incoherent synthetic aperture technology[116]. (a) Process for synthetic aperture super-resolution imaging based on time and aperture division synthetic aperture of phase reconstructive; (b) point spread function optimization based on time and aperture division synthetic aperture of phase reconstructive; (c) image comparison before and after super resolution

值得一提的是，严格意义上来说合成孔径技术通常不被称作“超分辨”技术，这是因为其不但单次测量是衍射受限的，而且合成孔径后仍然受限于由子孔径之和所决定的大孔径光学系统下的光学衍射极限，其并没有突破由光波波长所限制的光学衍射极限。此外，通常情况下合成孔径的原始数据都是基于低空间带宽的成像系统以牺牲时间分辨率获得的空间分辨率提升，因此必须在总的空间带宽（或分辨率）和时间分辨率之间做出权衡，这再次表明在使用“超分辨”这一术语时要足够谨慎。这强调了一个成像系统实现超分辨率的能力往往与其信息量或自由度的分解与重组相关，前者往往需要借助于光学调控机制来实现，而后者是需要数字化的信息处理形式来实现，而最终所“超”的分辨率需要通过另一个维度的“牺牲”来弥补。

5.3.2 结构光照明

另一种典型的基于频域调控的超分辨技术是结构光照明显微术（Structured Illumination Microscopy，SIM）。如前所述，成像系统的分辨率受到阿贝空间滤波效应的限制，存在接近波长一半尺度的衍射极限，物场信息中高于此光学传递函数截止频率的成分将会被滤除。针对这一问题，Gustafsson[117]于2000年提出了SIM技术，其基本原理是通过结构化照明在频域以空间混频的方式将物体高频信息载入光学系统的探测通带内实现突破阿贝衍射极限的超分辨光学显微成像。当利用周期性结构正弦照明光激发样品时，在频域上由于结构光频谱与物频谱的卷积而产生携带物体信息的多级频谱。其中±1级频谱将携带物体细节信息的高频部分平移至截止频率范围内而被探测，如图25(a)所示。但这些高频信息与0级频谱的低频信息叠加在一起，需要后期数据处理（如相移、反卷积、参数估计等）将三级频谱分开才能有效获得样品的高频信息[118]。由于结构光条纹照射在样品上也受到系统衍射限制，因此等效截止频率最多可拓展一倍，即SIM的分辨率最多能在衍射极限的基础上提高一倍，达到非相干衍射极限的2倍，约100 nm[119]。但光栅衍射效应不仅仅限于±1级频谱，例如矩形光栅的频谱就要丰富的多，其还包括±2级、±3级等高阶频谱。因此，假如能采用矩形光栅作为结构光，则可以产生多级频谱，使等效截止频率得到多次拓展从而大幅提高分辨率。但由于结构光的产生也受到光学系统有限孔径的限制，直接在物平面上形成一个周期接近衍射极限分辨率的矩形光栅并不现实。针对此问题， Gustafsson[120]在传统SIM的基础上进一步提出了饱和结构光照明显微技术（Saturated SIM，SSIM），巧妙地利用荧光分子的饱和激发使样品在正弦光波激发下发出具有高阶频率分量的非正弦结构光，从而实现多级频谱拓展（如图25(b)），将分辨率提高到了约50 nm的水平。然而，饱和照明所需的高强度激光增加了SSIM的光漂白，使其难以运用于活细胞成像，无法发挥SIM高光子效率、低光毒性的优势，因此并未得到广泛应用。相关结果见图25(c)～25(e)。

图25 结构光照明显微术。（a）传统（线性）结构光照明显微术的光路及频谱调制过程；（b）饱和结构光照明显微技术的频谱调制过程；（c）COS-7细胞中f-肌动蛋白的饱和SIM超分辨图像及不同方法的对比结果（左上：宽场，右上：反卷积，左下：SIM，右下：SSIM）；（d）不同方法下COS-7细胞中质膜微囊的超分辨图像（左上：宽场，右上：反卷积，左下：SIM，右下：SSIM）；（e） 活体COS-7细胞中质膜微囊的SSIM超分辨结果[117,120-121]Fig. 25 Structured illumination microscopy. (a) Optical train and spectral modulation process of conventional (linear) structured illumination microscopy; (b) spectral modulation process of saturated structured illumination microscopy; (c)SIM super-resolution images of f-actin in COS-7 cells and the comparison results with different methods (upper left:wide field, upper right: deconvolution, lower left: SIM, lower right: SSIM); (d) super-resolution images of caveolae in COS-7 cells with different methods (upper left: wide field, upper right: deconvolution, lower left: SIM, lower right:SSIM); (e) SSIM super-resolution results of caveolae in living COS-7 cells[117,120-121]

虽然在光栅调控方式上具有高度相似性，结构光照明技术与Lukosz超分辨率方案在具体实施上仍有几点区别。首先，光栅调制与形成的方式不同（物理光栅-光学结构光场），所以SIM光栅条纹同样受到系统衍射极限限制。其次，Lukosz超分辨率方案本质上是属于相干成像的范畴，而SIM技术实际上是一种非相干成像模态，所以二者在成像机理（复振幅探测-强度探测）与衍射极限上（相干衍射极限-非相干衍射极限）都有一些区别。最后，从处理方式上来看，SIM是通过数字重构来获得空间带宽积提升的，而非Lukosz超分辨率方案中的物理滤波。尽管如此，SIM技术与Lukosz超分辨率方案的本质思想是一致的。这种一致性当将SIM技术应用在相干成像系统中时尤为明显，如结构光照明数字全息显微术[122-123]。由于相干正弦光场本质上可以看作是2束（当存在直流分量时为3束）平面波干涉叠加形成的结果，此类相干SIM技术本质上就可以看作是相干合成孔径技术的一个（多孔径复用探测）特例[124]。

5.3.3 点扩散函数工程

除了上述从频域光学传递函数合成的方式来提升分辨率外，实现超分辨率同样也可以从空域角度考虑，即通过缩小空域点扩散函数的尺寸来实现。这类通过人为调控点扩散函数来实现超分辨成像的技术被称为点扩散函数工程。阿贝衍射极限公式源自严密的物理学推演，并在实践中经受了严格的检验，但其成立的条件是可以改变的。2014年，获得诺贝尔化学奖的超分辨率荧光显微技术利用荧光分子的开关效应的发现和单分子探测技术，使连续观测单个荧光分子行为而非其集合平均成为可能。受激发射损耗显微（Stimulated Emission Depletion，STED）[11]、光敏定位显微（Photo Activated Localization Microscopy，PALM）[13]、随机光学重建显微（Stochastic Optical Reconstruction Microscopy, STORM）[12]等超分辨成像利用荧光分子的受激辐射原理与光开关效应绕开了阿贝衍射极限，将光学显微技术带入到纳米尺度。这些技术都离不开对成像系统PSF的人为调控。

基于PSF函数调制的超分辨技术的代表为Hell[11,125-126]所提出的STED技术。如图26所示，STED采用两束共轴激光，分别为激发光和损耗光。在激发光的照射下，基态的荧光分子吸收光子跃迁到激发态并发射出荧光；再使用环形损耗光将第1束光斑周围的荧光物质通过受激损耗过程灭活，只保留位于中间部位的纳米尺度区域以减少荧光光点的衍射面积，通过扫描记录即可获取整个样品的完整图像[127]。STED显微镜的横向分辨率可达20～70 nm，凭借超高的分辨率，STED很快被应用于生物细胞研究并取得一系列重要的新发现[127]。但是，由于STED本身属于点扫描成像技术，为了提升成像速度，STED通常需要高的激发强度来记录足够的光子以换取时间分辨率，所导致的光毒性和光漂白限制了STED在活细胞成像中的应用。

图26 STED的超分辨原理示意图和结果图。（a）STED典型光学系统；（b）STED超分辨原理；（c）微管宽场图像；（d）微管超分辨图像[128]Fig. 26 The schematic diagram and results of super-resolution STED. (a) A typical STED setup; (b) the principle of STED;(c) the wide-field image of microtubules; (d) the super-resolution image of microtubules [128]

Betzig[13]等提出的PALM技术基于荧光分子的光转化能力和单分子定位，通过用光控制每次仅有少量随机离散的单个荧光分子发光，并准确定位单个荧光分子点扩展函数的中心，最终利用多次曝光叠加成一幅超高分辨率图像，如图27所示。由Hess[129]提出的荧光活化定位显微术（fPALM）与PALM原理相似，荧光团经探测器成像后，由光强控制荧光分子被可逆地灭活或不可逆地光漂白而从视场中消失。庄小威[12]提出的STORM与PALM技术在原理上类似，区别在于其所利用的探针是化学小分子（Cy3和Cy5、Cy7等）而不是生物大分子。基于单分子定位的超分辨显微成像技术可实现10～30 nm的横向分辨率，但由于反复激活和淬灭荧光分子，所需时间长，其时间分辨率较低。

图27 PALM的超分辨原理示意图与结果图。（a）探测的单个原始光子图像；（b）对（a）的高斯拟合；（c） 定位的（a）的中心；（d） 聚苯乙烯微球的宽场图像；（e）叠加原始PALM堆栈数据中单分子图像所获取的聚苯乙烯微球图像；（f）聚苯乙烯微球的PALM超分辨图像Fig. 27 Schematic diagram and result diagram of PALM super-resolution imaging. (a) Detected single raw photon image;(b) Gaussian fitting of (a); (c) localized center of (a); (d) wide-field image of plain polystyrene beads; (e) the plain polystyrene bead image obtained by superimposing the single molecule images in the entire PALM data stack;(f) PALM super-resolution image of plain polystyrene beads

上述STED、PALM和STORM超分辨成像技术理论上可将显微成像系统的有效PSF尺寸无限压缩，极大提高系统的分辨率，但它们都需要对样品进行复杂的荧光标记，这就局限了显微样品的种类，并且这类技术对荧光探针也有较高的精度要求。如何在不采用荧光标记的前提下缩小PSF尺寸，提升成像系统的分辨率对天文学、遥感监测、无标记显微和光学数据存储等领域具有重要意义。由于成像系统的PSF由光瞳函数所决定，因此可以通过调制光瞳函数（振幅、相位与偏振）实现对PSF的调控。该问题由Toraldo di Francia[130]于1952年进行了系统阐述与研究。他指出通过构造由离散环状狭缝组成的系统孔径，可以减小PSF中心光斑的尺寸。通过仔细设计同心环半径，可以减小中心的光斑大小，当焦斑主瓣宽度小于衍射极限时，则实现了超分辨成像。该想法随后被许多学者通过理论与实验得以证实[131-134]，并广泛应用到光刻和光存储等领域。实际上，该光瞳滤波技术与后来报道的超振荡透镜在思路和形式上都非常相似。在第2.3节中所讨论的阿贝成像原理表明，成像系统对物光场而言相当于一个低通滤波器，其截止频率决定了成像系统所能观察到的最小特征。因此，当光场通过成像系统后在像面形成的是一个带限信号。一般来说，带限函数的振荡速度是不可能高于其最高傅立叶分量的，但超振荡现象的发现恰好反驳了这一点。超振荡现象的本质就在于带限函数在局部区域振荡得比其最高傅立叶成分更快，其首次由Aharonov等[135]和Berry[136-137]引入到光学聚焦中。超振荡的发生可以解释为信号的局部频率，或者说相位梯度超过信号傅立叶频谱中的最高频率分量。对于二维光场信号，超振荡的发生与相位奇异性（非连续性跳变或振荡）有关[138]，并且可以很容易地在散斑场中观察到[139]。超振荡焦斑通常尺寸上要小于 0 .38λ/NA[140]，显著优于瑞利判据的 0.61λ/NA，因此为远场的超分辨聚焦和成像提供了新的思路。

值得注意的是，这里将超振荡归类于Lukosz型超分辨方案的原因是超振荡所带来的分辨率提升效应也是需要付出代价的。一方面，超振荡现象常伴随着较低的主瓣强度和高强度的旁瓣。因此，可用的视场范围非常有限，通常需要以牺牲视场换取分辨率的提升。此特性使其非常适合与共聚焦点扫描机制的显微镜相结合（因为该类技术本身就需要牺牲视场或者时间分辨率），如图28所示[141]。另一方面，对于一个固定振幅的超振荡窗口，信号能量随着超振荡的数量呈指数增长，并随着信号带宽的倒数呈多项式增长[142]。这就意味着随着超振荡效应的提升，大部分的信号能量会停留在超振荡发生窗口之外，从而需要牺牲信噪比（或斯特列尔比，Strehl Ratio）以换取分辨率的提升。这与Feirreira和Kempf[142]所指出的信号动态范围的指数增长符合香农信息理论不谋而合：如果成像系统空间带宽积为SBP，其可以传输信息的比特数为S BPlog2(1+S NR)。如果想要提升分辨率，即增加超过空间带宽乘积的信号特征量，必须要牺牲信噪比，即每个单位符号所携带的信息量。因此，在设计超分辨率孔径或者超震荡透镜时，必须在分辨率（PSF尺寸）、视场、信噪比之间进行平衡[143]。

图28 基于超振荡透镜的共聚焦显微镜，右上角的插图显示了超振荡光斑的光强分布[141]Fig. 28 Principles of confocal microscopy with superoscillatory illumination. The inset in the upper right corner shows the intensity distribution of a superoscillatory hotspot[141]

6 （图像）超分辨成像——基于广义采样的视角

从上节可知，Lukosz的超分辨方法仅仅对信号的相空间分布进行调控与重排列。而本节将在相空间中解释采样与插值，这不仅仅是为了在空间域和频域同时揭示对采样定理的理解，还展示了将其概念基于Lukosz的空间带宽积调控思想相关联与拓展的可能性。这将为解释另一类超分辨技术，即突破像素离散采样频率限制的图像超分辨成像技术提供独特的视角。

6.1 相空间采样与Papoulis带宽压缩

光学图像在相空间内的表征特性就如同不可压缩的流体，虽然它灵活可控，但总体积守恒。想要压缩相空间的一个维度，必须牺牲其他的维度。可以将同样的概念应用于香农-奈奎斯特采样定理——空域离散采样在相空间中对应沿频率v轴复制频谱，并沿x轴离散化维格纳分布函数[144-145]。而其逆过程插值对应于低通滤波器的维格纳函数在频率轴上的相乘和在空间域中的卷积。

为了理解相空间采样的核心思想，以Papoulis带宽压缩[146]的相关样例来说明。如图29所示，原始（带限）信号(a)通过透镜啁啾（即信号与二次相位函数的乘积）与分数阶傅立叶变换后，其PSD也相继经过平行于v轴方向的剪切（图29 (b)）以及旋转后，形成了另一个带限函数（图29(c)）。其PSD与x轴重新平齐，但带宽发生了改变。

图29 通过线性光学变换进行带宽压缩。（a）带限函数的相空间图；（b）啁啾后的PSD；（c）经过分数傅立叶变换恢复带限函数后的PSDFig. 29 Bandwidth compression via linear optical transformations. (a) Phase-space diagram of band-limited function; (b) PSD after chirping; (c) PSD after fractional Fourier transformation to recover band-limited function

显然上述Papoulis带宽压缩是以空间轴延展（Δx增 加到Δx′）为代价的，空间带宽积总量并不发生改变，这本质上与Lukosz超分辨率的空间带宽积调控相一致。

6.2 相空间广义采样定理

可以进一步将相同的概念应用于空间带宽有限但频域带宽无限的信号（图30(a)）。当其在自由空间传播（菲涅尔衍射）时，该信号的空间带限性就会被打破，如图30 (b)所示。因为其PSD不再是长方形条状，在空间域不论如何进行直接采样都会导致在频域中非带限信号的直接复制，从而不可避免地造成混叠。然而，当能够采用分数阶傅立叶变换对信号进行去啁啾时，就能够将其频域转换到紧凑支持域，此时再对信号进行高于Δvs频率的采样就可有效地避免混叠问题，如图30 (b)所示[70]。另一方面，还可以暂且不顾混叠，对信号进行高于Δvs频率的采样，然后在插值恢复之前对信号进行去啁啾，或者等价地说把去啁啾结合进入内插公式中，同样可以去混叠并恢复连续信号[147]。上述过程揭示了一个信号只要在相空间沿着某一个方向或者联合维度是紧凑的，它就能够通过空间带宽调控的方式在不丢失信号信息的情况下获得对其离散采样，其最小采样频率是由其相空间最紧凑维度上的局部带宽决定的。该思想可以被认为是香农-奈奎斯特采样定理的拓展，我们将其称为相空间的广义采样定律。正如图30 (b)～30(c)所示，不管采用何种相空间变换，该信号的最小采样间距是由其相空间的局部带宽决定的。

图30 菲涅尔全息图的广义采样。（a）空间紧凑的信号的相空间图；（b）采样域中的信号；（c）图（b）中去啁啾后的信号Fig. 30 Generalized sampling of Fresnel holograms. (a) Phase-space diagram of a signal compact in space; (b) signal in the domain of sampling; (c) signal in (b) after dechirping

6.3 Papoulis广义采样

区别于相空间的广义采样定理，Papoulis从另一个角度提出了另一种广义抽样展开概念，其为实现图像亚像素超分辨提供了数据采集方案基础，可广泛应用于分析时间多次编码采样或者空域并行多孔径系统。这些系统的任务可以定义为用多个小空间带宽积系统对一个大空间带宽积信号进行采集，或者一个小空间带宽积系统通过多次采样对一个大空间带宽积信号进行采集。Papoulis广义抽样为分析与解读这些超分辨、或者空间带宽积拓展的计算成像技术提供了一个通用的理论框架[17-18]。

Papoulis广义采样指的是通过对一个信号u(x)（它可以是有带宽限制的，也可以是没有带宽限制的）以M个相应的点扩散函数hm(x)进行抽样调制，经过系统低通滤波与离散化采集后降采样的gm(x) 恢 复连续信号的估计值uˆ(x)的过程。这本质上是一个多元联合解卷积问题，或者等价于线性方程组的求解问题。而该方程组的解的存在性与唯一性，取决于点扩散函数hm(x)的形式与数量[148]。更具体来说，由系统点扩散函数hm(x)所构造的采样矩阵H本身要是可逆的。从物理角度说，每个子孔径对应的光学传递函数可以覆盖原信号所感兴趣的带宽Δv，也就是说在这个频带内的每个频率必须被至少一个子孔径所覆盖。此外，在传递函数多次覆盖的区域，它们的多次测量值间还需要具有一定意义上的正交性，以此保证对每个频谱信息进行无歧义恢复[148]。

以亚像素超分辨成像作为一个简单的例子来说明。可以把对场景的两次低分辨率采样当作是两个成像子系统，每个子系统的通带为Δv，且分别以奈奎斯特采样频率的一半对输出信号进行采样。如果两个系统在同一个位置采样，则它们的功能相同，此时，由于高频分量没有足够的信息去解混叠，所以无法恢复理想信号。但如果在两个测量值之间引入亚像素偏移，就会引起测量信号的差异，这就为恢复理想信号提供了有效的信息，如图31。与Lukosz型超分辨率类似的是，Papoulis广义采样实质上也是一种通过交换自由度来实现信息量提升的过程，其构成了实现多帧图像超分辨率与去混叠技术的基础。

图31 可控亚像素移动所引起的像素级光强变化Fig. 31 Pixel level light intensity change caused by controllable sub-pixel movement

6.4 压缩采样（compressive sampling）与压缩感知（compressive sensing）

上述采样技术虽然是香农-奈奎斯特采样定理的拓展，但它们成立的前提仍然受到采样定理本身的限制。而压缩采样理论则认为可以通过远少于传统香农-奈奎斯特采样的次数来恢复图像，该理论亦被称为压缩感知[149-150]。为了实现这一点，压缩采样依靠两个准则：稀疏性（sparsity）与非相干性（incoherence）。也就是说大多数自然信号是稀疏且可压缩的，它们在合适的基下有更紧凑的表示，即信号在某个域中非零点很集中，远远小于信号总点数。而误差、干扰、噪声或者与信号无关的成分，在此基下则有着稠密的表示。

压缩采样与压缩感知突破奈奎斯特采样定理的关键就在于其采样的方式。当提到“采样频率”的时候，意味着做的是等间距采样，数字信号领域通常都是做等间距采样，但是压缩感知采用不等间距采样，比如采用随机亚采样，这时候频域就不再是以固定周期进行延拓的了，而是会产生大量不相关的干扰值。这些频率泄露均匀地分布在整个频域，但因为相比核心成分而言赋值较小，通过“压缩”排除它们的干扰，为信号的高信噪比恢复提供了可能。压缩感知理论的核心问题是信号的稀疏表示、观测矩阵的设计和重构算法，信号本身或在变换域中的系数越稀疏，观测矩阵和稀疏基构成的压缩感知矩阵的受限等距常数越小，则压缩感知的性能越好。而重构算法通常以原始信号和信号估计之差的L1范数作为目标函数，并通过非线性迭代优化的方式实现。

压缩采样所代表的基本思路是从尽量少的数据中提取尽量多的信息，这毫无疑问是一种极具应用前景的理论与思想。它是传统信息论的延伸，但是又超越了传统的采样理论，成为了信息论的一门崭新子分支，在计算光学成像领域得到了广泛关注[151-152]。但我们仍需注意，信息本质上不会无中生有，压缩采样的成立是有条件的。L1范数最小化本质上蕴含了目标分布的先验信息（如分片平滑性），该先验信息的准确性决定了数据压缩比以及信号重建的质量。

6.5 （图像）超分辨成像的典型计算成像案例

随着光学成像到光电数字化成像的转变，图像需要通过图像传感器件进行数字化离散采样和记录。这一过程要求能够记录光学图像的完整信息，以应对后续的观察和处理，图像的像素分辨率也是成像系统进行采样的“最后一道工序”。根据奈奎斯特采样定律知，当探测器的像素大小大于所探测光强最高余弦频率分量周期的1/2时，会发生像素混叠。如图32(a)所示，此成像过程可以等效为光强先经高分辨率像素网格采样（不发生混叠），然后进行一次像素合并，相邻高分辨像素合并为低分辨率像素的过程（发生混叠，如图32 (b)）。像素超分辨的本质就是将低分辨像素重新分解成高分辨率像素，并获取每个高分辨率像素响应相对于低分辨率像素的权重（图像细节成分），如图32(c)所示。这本身也是一个从无到有的过程，因此，超分辨率的优化重建本质上是一个病态方程的逆向求解问题。高维病态问题的不确定性即解的不可预测性，可以通过构建系数矩阵，将病态问题正定化，从而实现病态问题的优化求解。归根到底，超分辨率重建技术本质上就是采用光学调控的方式，通过交换自由度来实现信息量提升，从而打破成像系统的固有限制，实现图像超分辨率重建与去混叠。其本质都是将信号通过调制解调的方式，以牺牲某一维度（时间）的信息来换取另外一个维度（空间）上的信息提升，或通过构造函数或算法将信号无失真或近似地恢复，从而实现滤波、去噪和去伪影等功能。

图32 图像亚像素超分辨。（a）图像降采样正向模型；（b）采样频率不足产生频谱混叠效应；（c）亚像素位移超分辨重建示意图Fig. 32 Image subpixel super-resolution. (a) Image downsampling forward model; (b) spectral aliasing effect due to insufficient sampling frequency; (c) schematic diagram of subpixel shift super-resolution reconstruction

超分辨率重建通常以构建正向物理模型以及学习外部样例等方式引入先验知识，使得超分辨率重建问题的解具有唯一性，重建出理想的高分辨率图像。目前图像（像素）分辨率成像技术大致可分为两类，即单帧图像超分辨[153-155]和多帧图像超分辨[156-157]。

6.5.1 单帧像素超分辨技术

单帧图像超分辨重建技术仅从一幅低分辨率图像中即可重建对应的高分辨率图像，其也可以看作是图像插值的特例。显然，从一幅静态图像进行像素超分辨率是一个病态逆问题求解过程，但在图像质量较高而噪声较低且放大系数较小的情况下，可以通过引入某种先验模型或使用特定的匹配机制在原始图像上进行插值，以提升图像的视觉效果。

单帧图像超分辨方法主要包括频域外推[158-159]、正则化[160]、实例映射[161]以及深度学习[162-165]等。稀疏性可以作为约束或者正则项，提供额外的先验信息。而大部分信号本身并不是稀疏的（即在自然基下的表达不是稀疏的），但是经过适当的线性变换后是稀疏的（即在另一组基下是稀疏的），如离散余弦变换与小波变换等。这样就可以使得采样速率完全由信号中包含的信息所决定，而不再受限于信号的带宽，从而打破了传统信息处理需满足奈奎斯特采样的局限性，在信号处理领域开辟了全新的研究方向。其基本思想也是如何利用尽可能少的信息恢复得到高维信息。压缩感知用非自适应线性投影来保持信号的原始结构，通过编解码的方式，以远低于所需的采样频率对原始信号进行采样，并通过后端数据处理的方式对原始信号进行重建恢复，有效减小了传感器的计算压力与数据的传送、储存成本。与此同时，压缩感知目前也存在一些问题和瓶颈，主要集中在系数矩阵的构建与重建求解上，例如测量矩阵与稀疏基的非相关性难以保证，稀疏矩阵构建的复杂性，稀疏求解的不确定性等。

近年来，人工智能与深度学习技术的飞跃式发展为计算光学成像技术开启了一扇全新的大门，也同样再次助推单帧图像超分辨图像[166-169]的革新，将传统物理模型驱动的图像复原转为基于数据模型驱动的图像间映射问题，或是物理模型与数据模型的联合优化设计。深度学习技术[170-172]通过输入图像中不同尺度上的内部相似性或者从外部低分辨率和高分辨率样本中进行学习建立学习映射函数来恢复其最可能的高分辨率版本，如图33（彩图见期刊电子版）所示。然而由于单帧图像所包含的信息本身十分有限，故所能达到的分辨率提升效果会受到极大限制。更重要的是，额外的高频信息往往是通过“图像先验”[173-174]与“样本学习[175]”所得到的，因此重建所获得的“最有可能”的高分辨率版本通常情况下只能在视觉上达到较高的清晰度，但不能保证提供真实的目标图像高分辨率细节。

图33 基于深度学习的单帧图像超分辨图像重构算法[184]。（a）基于图像特征提取的单帧图像超分辨率神经网络结构框图；（b） 单帧图像神经网络超分辨重构结果。虽然图像细节变清晰了，但大多与真实图像并完全不一致Fig. 33 Single-frame super-resolution image reconstruction algorithm based on deep learning[184]. (a) Block diagram of singleframe image super-resolution neural network structure based on image feature extraction; (b) results of single-frame image neural network super-resolution reconstruction. Although the image details become clearer, most of them do not match with the real image at all

进而，基于物理模型先验[176-178]的深度学习求解思想也相继提出，将复杂的问题分解为若干简单子问题或子步骤与深度神经网络的联合优化求解，或是将成像系统的点扩散函数[179-181]（或光学传递函数）模型映射到深度学习网络中，同时将光学系统拍摄到的图像与传递函数作为“网络输入”，将待恢复的期望信息作为“网络输出”通过高维度特征拟合实现图像与信息的提取与重建。此外，通过构建真实数据集[182-183]，建立场景与图像之间的正向模型，并使得采样数据包含场景中所感兴趣的物理信息，提供模型重建的稳定性以及可靠性。

6.5.2 多帧像素超分辨技术

1977年，Papoulis A首次引入广义采样理论[17]，对Shannon采样定理进行推广，探讨符合Nyquist采样率的条件下，线性时不变系统带限信号的采样与重构问题。进一步User M和Zerubia J在Papoulis A理论基础上，将信号空间拓展到非带限情况，将信号的重构问题转向空间投影与信号在其子空间或投影空间的逼近[148,185]。而多帧图像超分辨的核心思想在于利用时间带宽（获取同一场景的多帧图像序列）换取空间分辨，构建病态逆向问题的求解矩阵。采用照明端或成像端调控的方式，建立场景与成像端之间的变换或调制模型，通过迭代算法优化进行计算反演，以获得目标场景的高质量图像与高维度物理信息。正如Papoulis广义采样所指出的，超分辨重建问题本质上是一个多元联合解卷积问题，或者等价于线性方程组的求解问题。若给予足够数量的观察图像，系统的求解方程将是正定矩阵或超定矩阵，使高分辨图像复原成为可能。从物理角度讲，由系统点扩散函数所构造的采样矩阵H本身要是可逆的，并且在实际成像中也包含着成像系统干扰项及大气扰动等外部影响因素，因此逆向矩阵构建的稳定性（条件数）代表了成像模型对噪声的敏感性，它直接影响高分辨图像的恢复效果。因此，Papoulis广义采样实质上也是一种通过交换自由度来实现信息量提升的过程，其构成了多帧图像超分辨率与去混叠技术的基础（图34）。

图34 多帧图像超分辨基本原理。通过进行不同的调控方式使得点扩散函数（采样矩阵）产生像素级的光强变化Fig. 34 The basic principle of multi-frame image super-resolution. The point spread function produces pixel-level light intensity variations (sampling matrix) by performing different modulation methods

空间混叠意味着高频成分被折叠并加入到低频成分中，通过获得几个具有不同空间混叠效应的测量，这些高频成分可以被识别和恢复，但如果在两个测量值之间引入亚像素偏移，从而引起测量信号的差异，这就为理想信号恢复提供了有效的信息。因此，传统的多帧图像超分辨算法大多数通过探测器与观测场景间的可控亚像素位移来产生这些具有光强多样性的低分辨图像的，通过对同一场景的多次采样，最后采用重构算法恢复出高分辨率图像。基于被动亚像素位移的超分辨重建算法研究较为成熟，大部分算法是从图像盲复原引入的，还可以细分为频域法[186]，非均匀内插法[187]等。在经典多图像超分辨中，对同一场景中的低分辨率图像进行亚像素位移，对高分辨率图像进行重构，这只需移动相机即可实现，如图32(c)所示。然而，由于非理想光学传输、非均匀采样[187]及配准误差[188]问题，这种方法通常仅限于分辨率的小幅度提高。

实现图像亚像素偏移的另一类关键技术是通过主动微扫描的方式获得光学系统和探测器之间的可操纵位移[189-192]，以获取像素级的光强变化。微扫描可以看作是一个过采样的过程（图35），它通过压电陶瓷、扫描振镜或平板旋转来实现，通过高精度微扫描装置使得探测器所采集图像分别在x，y方向进行等间距的亚像素位移，得到多帧具有不同方向、不同位移的混叠图像。通过已知的不同方向的位移量，结合采集的图像进行数据重组即可重建得到一张去混叠图像，从而实现超像素分辨成像。微扫描技术的应用比较广泛，特别是在现代军事夜视与红外成像制导应用方面占有极其重要的地位。主动微扫描图像超分辨技术[193]有效解决了被动多帧图像超分辨中的非全局平移、配准误差、以及采样不均匀的问题，有效促进了分辨率稳定且各向同性的提升，但采集装置存在着系统结构复杂，加工精度高，位移量及扫描路径不易控制，对环境振动敏感等缺点[194]。

图35 微扫描装置。（a）光学折射法；（b）平板旋转法；（c）压电陶瓷体Fig. 35 Micro-scanning device. (a) Optical refraction method; (b) flat plate rotation method; (c) piezoelectric ceramics

针对上述问题，本课题组提出了基于孔径编码的像素超分辨成像方法[195]。从“编码、混叠、采样”正向建模过程出发，同时考虑点扩散函数的各项异性、频谱的覆盖率与响应度，通过构建多元联合解卷积方程寻找最优编码图案，突破探测器空间采样限制，实现图像去混叠。该方法与传统的基于亚像素位移的多帧图像超分辨率方法的根本区别是，成像过程并不依赖于场景和探测器之间的相对运动，且明确考虑了成像系统的衍射效应。如图36所示，编码孔径像素超分辨成像技术的基本思想是通过改变不同的孔径模式来调节成像系统的点扩散函数，使得点扩散函数可以跨越多个整像素，并包含有关高频图像的信息。成像系统在不同孔径编码调控下对同一场景进行多次采样，然后将所拍摄到的低分辨率混叠图像在频域进行迭代重构与解混叠，最终可反演出目标场景中小于像素尺寸的高频细节成分。实验结果如图37所示，采用该技术可使成像系统的分辨率提升至探测器物理尺寸所限制的奈奎斯特采样频率的3倍以上，进而实现“亚像素”成像。该方法其实是点扩散函数工程与Papoulis广义采样理论在像素超分辨成像领域的创新结合，其不借助于物理移动器件或空间扫描机制，为突破探测器空间采样不足所造成的分辨率受限提供了一条崭新的思路。

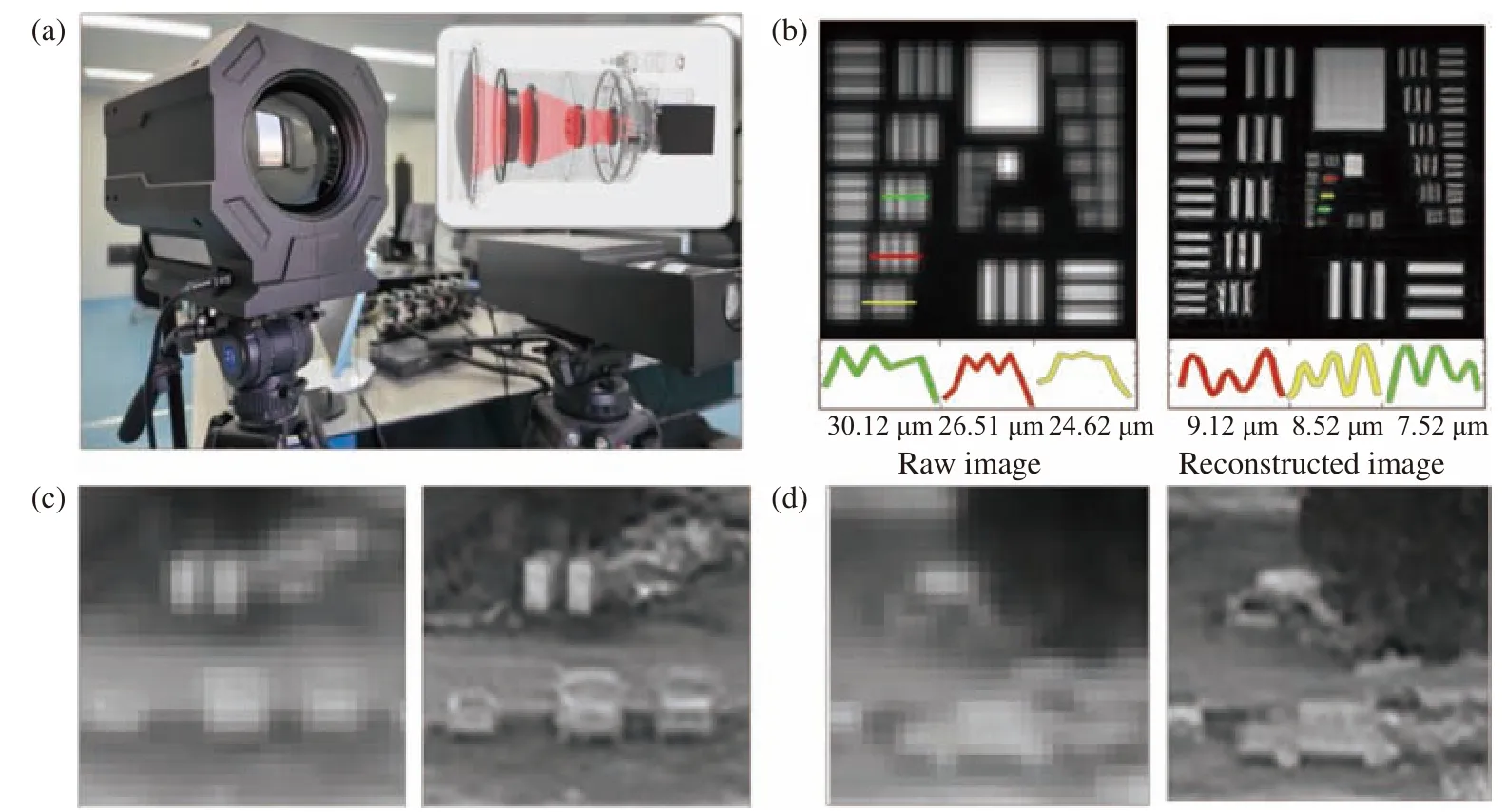
图37 基于孔径编码的像素超分辨成像技术的典型实验结果[116]。（a）长波红外成像系统对标准分辨率靶标成像测试；（b）～（d） 采用像素超分辨算法对USAF靶标及远距离车辆前后成像效果对比Fig. 37 Typical experimental results of coded aperture-based pixel super-resolution imaging technique[116]. (a) Long-wave infrared imaging system for standard resolution target imaging test; (b)-(d) comparison of imaging resolution before and after applying pixel super-resolution algorithm on USAF target and vehicle

7 空间带宽积拓展——扩视场vs超分辨

图像空间带宽积是其奈奎斯特极限下完整表示信号所需的采样样本数，即其有效可分辨像元的数目。而受光学系统空间带宽积守恒原理所限，对于传统成像系统而言，通过镜头聚焦并被成像设备采集到的物体的信息量，也就是其空间带宽积总是有限的，大约在千万像素量级（10 Megapixels）。图像空间带宽积取决于两方面因素——视场与分辨率，因此图像空间带宽积的扩展也必须依赖于视场的扩大与分辨率的提高两方面共同完成。

7.1 基于视场扩大的空间带宽积拓展

扩大视场是提升空间带宽积，获得宽视场高分辨图像最直接的方式。其又可以分为单成像系统扫描拼接与多探测器/多孔径合成两类技术。单成像系统扫描拼接是以时间分辨置换空间分辨的传统带宽积拓展方式。图38为美国卡耐基梅隆大学设计开发的Gigapan全景拍摄系统[196]，通过围绕一个固定轴进行连续扫描拍摄，获取不同视角下的图像，然后通过后期图像拼接处理，最终获得了约十亿像素级的宽视场超高分辨率图像。在理想情况下（忽略视场重叠区域），所获得图像的最大空间带宽积由单幅图像的空间带宽积与曝光次数的乘积决定。

图38 Gigapan全景拍摄系统及拍摄拼接所得的像素全景图Fig. 38 Gigapan panoramic imaging system and the gigapixel panorama image obtained by stitching

多探测器/多孔径合成是在同一时刻使用多个成像设备对空间场景进行并行拍摄。每个相邻成像设备之间均有一定视场的重叠，最终通过拍摄图像拼接获得宽视场高分辨图像。这种方法无需旋转扫描机械结构，解决了单相机扫描拍摄的时间分辨率低的问题。依照视场拼接方式的不同，其大致包括探测器拼接、多相机拼接和多尺度成像等方式。

7.1.1 多探测器拼接

近来年，随着航天遥感、天文观测、广域监视等领域的发展，单片探测器的像素规模已经不能满足要求。多探测器拼接技术利用多片探测器实现了像素的互补，通过光学系统分光并投射于各个探测器感光面实现多幅图像获取，并借助光学拼接成像技术实现了广域超高分辨图像合成探测。如Microlensing Observations in Astrophysics(MOA) 项目的第三代成像组件MOA-cam3[197]，其由10片像素数为 2000×4 000的CCD4482芯片按5×2组成，经过特殊封装, 可实现多个侧面拼接，如图39 (a)所示。欧洲空间局（ESA）建造的大型天文望远镜Gaia[198]的焦平面阵列由106片CCD拼接而成，如图39 (b)所示。单片CCD像素数为4 500×1966，可实现总像素数可达9.4亿广域图像。由华盛顿大学和其他研究机构的科学家研究的大型综合巡天望远镜（Large Synoptic Survey Telescope，LSST）[199]的焦平面阵列由189个4 096×4 096像素数的CCD探测器组成，如图39 (c)所示。LSST三天全天区拍摄一次，可以实现320～1 060 nm波长范围的6个波段上20 000平方度天区的连续重叠成像，像素规模达到30亿。如图39 (d)所示，由中国科学院国家天文台承担建造的大天区面积多目标光谱天文望远镜LAMOST[200]包含一个反射施密特校正镜，包含24块正六边形子镜片，每片镜片的口径在3.6～4.9 m之间，通过我国自主研制的镜面拼接技术，将接收到的包含天体光谱信息的光束反射到光纤探头并传输到CCD上，可同时观测4 000个天体。

图39 多片探测器进行集成与拼接。（a）由10片CCD4482芯片组成MOA-cam3；（b）由106片CCD 拼接而成的Gaia天文望远镜的焦平面阵列；（c）由21个模块组成的大型综合巡天望远镜LSST（Large Synoptic Survey Telescope）的焦平面阵列。每个模块由9个CCD 探测器组成；（d）由24块正六边形的镜片拼接组成的大天区面积多目标光谱天文望远镜的改正镜Fig. 39 Integration and stitching of multiple detectors. (a) MOA-cam3 is composed of 10 CCD4482 chips; (b) the Gaia Astronomical Telescope's focal plane array consists of 106 CCDs stitched together; (c) the focal plane array of the Large Synoptic Survey Telescope (LSST) is composed of 21 modules. Each module consists of 9 CCD detectors; (d) the correction mirror of large sky area multi-target spectral astronomical telescope is composed of 24 hexagonal lenses

除了天文观测外，多片探测器进行集成与拼接技术还广泛应用在军工探测领域。例如美国空军实验室和LosAlamos国家实验室联合研制了AngelFire大视角持久监视观测系统，英国Logos Technologies公司研制了高分辨率广域昼夜监视系统Kestrel，英国BAE公司研制了搭载在A160T蜂鸟无人直升机上的ARGUS系统[201]等。如图40所示，ARGUS系统采用了368个Aptina MT9P031商用图像传感器和4个主镜头，其中92个传感器为一组，共用一个主镜头。92个探测器呈棋盘状分布，4个焦平面阵列交错互补，再通过图像拼接，能够得到较好的整体大视场高分辨率图像，总像素数为18亿。该系统飞行高度为6 km，可覆盖直径为7.2 km、面积为40平方公里的地面区域，地面像元分辨率可达15 cm，对覆盖区域内的人、车辆以及景物清晰可辨。

图40 ARGUS-IS系统及其成像效果。（a）ARGUS-IS 系统外型；（b）系统采用了368个图像传感器和4个主镜头，其中92个传感器为一组，共用一个主镜头。通过巧妙设置传感器的安装位置，使得每组传感器获得的图像错位，互为补充，再通过图像拼接，能够得到较好的整体成像结果。（c）此成像系统在6 000 m高空有效覆盖7.2 km×7.2 km的地面区域Fig. 40 ARGUS-IS system and its imaging results. (a) ARGUS-IS system appearance; (b) the system adopts 368 image sensors and four main lenses, of which 92 sensors are in one group and share one main lens. By skillfully setting the installation position of the sensors, the images obtained by each group of sensors are misaligned to complement each other, and then by image stitching, a better overall imaging result can be obtained. (c) This imaging system effectively covers a ground area of 7.2 km×7.2 km at 6 000 m altitude

7.1.2 多相机拼接

多相机分视场组合成像是使用多个小相机组成的相机阵列在同一时刻拍摄多幅有一定视场重叠的子图，再拼接得到广域视场合成图像。相机阵列的排列方式根据应用场景的不同而变化，包括平面型、环型、球型、仿生复眼型等。典型案例包括：2005年，斯坦福大学Wilburnden等人提出的一种由96个相机组成的大型成像系统，其可实现室内场景或室外特定场景的拼接成像，如图41(b)与41(c)所示。Lytro公司所研制的光场采集系统Immerge（如图41(a)）打破了多相机拼接场景的限制。该系统每个相机均配有单独的数据处理器，并且可以单独调控自己相机分布，拍摄出来的子图可以适应场景的变化，从而可以实现宽视场高分辨率视频图像采集[202-203]。借助于每个相机在不同视角分布的优势，该技术还可用于三维重建（如图41(d)所示的用于3D扫描技术的CAMatrix环型相机阵列系统）与光场渲染（如图41(e)所示的来自清华大学戴琼海院士课题组的鸟笼状相机阵列系统）等。

图41 多相机拼接系统。（a）Lytro公司所研制的光场采集系统Immerge；（b）斯坦福半环型相机阵列系统；（c）斯坦福平面型相机阵列系统；（d）CAMatrix环型相机阵列系统；（e）清华大学鸟笼相机阵列系统Fig. 41 Multi-camera stitching system. (a) Immerge, a light field acquisition system developed by Lytro; (b) Stanford semiring camera array system; (c) Stanford planar camera array system; (d) CAMatrix ring camera array system;(e) Tsinghua University birdcage camera array system

在仿生复眼成像方面，瑞士洛桑联邦理工学院（EPFL）的科研团队设计并研制了仿生复眼成像设备Panoptic[204]，如图42(a)所示。该成像系统由上百个“子眼微相机”组成并分层排布在一个半球面上，可覆盖较大的视场范围。在Panoptic系统的基础上，该科研团队进一步研发了大视场高分辨率的OMNI-R系统和Giga EYE系统[205]。其中OMNI-R系统由44个焦距为6 mm，视场为53°×43°的子眼镜头组成，如图42(b)所示，可以实时成像的视场范围为360°×100°。类似于昆虫复眼结构的还有美国北卡罗来纳州立大学天文学家Nicholas Law研制的艾弗里地基望远系统（Evryscope）[206-207]。该系统由24个口径为7 cm的望远镜组成，24个望远镜排布在半球壳上，如图42(c)所示，每次曝光可以获得约1/4个天空的视野。

图42 仿生复眼成像系统；（a）瑞士洛桑联邦理工学院（Swiss Federal Institute of Technology Lausanne，EPFL）的科研团队设计并研制了仿生复眼成像设备Panoptic；（b）大视场高分辨率的OMNI-R系统；（c）Nicholas Law研制的艾弗里地基望远系统EvryscopeFig. 42 Bionic compound eye imaging system; (a) Bionic compound eye imaging device Panoptic designed and developed by a research team at the Swiss Federal Institute of Technology Lausanne (EPFL); (b) large field of view high-resolution OMNI-R system; (c) Avery ground-based telescope Evryscope developed by Nicholas Law

7.1.3 多尺度成像

多尺度光学成像是另一种可同时实现宽视场和高分辨成像的方法。区别于前文介绍的几种成像方法，该方法是基于透镜系统的比例法则，从通过光学设计校正光学系统像差的角度出发来拓展成像系统的空间带宽积。针对大尺寸光学系统几何像差大的问题，美国杜克大学的Brady提出了多尺度光学成像设计方法[208]，采用光学设计的手段减少系统的几何像差。其主要思想是将系统成像过程划分为大视场粗糙成像与小视场高分辨成像两部分。大视场粗糙成像采用置于系统前端的主球透镜头对空间大角度光能进行收集实现，而小视场高分辨成像则采用位于主透镜后端的小透镜阵列对不同视场处的像差进行校正并配合使用与透镜阵列相对应的探测器阵列来实现。最终，借助信号处理单元将多通道获取的具有一定重叠的高分辨图像进行快速并向配准，拼接得到一幅完整的大视场高分辨图像。

虽然采用多尺度光学系统拓展成像系统空间带宽积具有很大的优越性，但是系统对主镜的选择有很高的要求。若以常规的透镜作为系统主镜，组成次级成像的多孔径中继阵列所需要校正的局部视场像差各不相同，这会很大程度增加中继阵列的加工与设计的难度。针对这一问题，Brady等人提出了同心多尺度光学成像系统[209-215,2]，使得次级成像系统所需要校正的局部像差对称，基于此，他们先后研制了应用于可见光波段的多尺度大视场高分辨率成像系统AWARE-2[2]、AWARE-10[216]、AWARE-40[217]，如 图43所 示。AWARE-2与AWARE-10均采用一个双层同心球透镜作为前级系统，分别以98个微相机以及382个微相机构成中继成像阵列；AWARE-40则采用一个非同心的双高斯物镜作为前级系统，从而增加了前级系统物镜的焦距，以262个微相机构成中继成像阵列。上述的多尺度成像系统均能够实现大视场高分辨成像，且获取图像的有效像素个数均可达十亿以上。

图43 多尺度成像系统。（a）AWARE-2结构图；（b）AWARE-10结构图；（c）AWARE-40结构图Fig. 43 Multiscale imaging system. (a) AWARE-2 architecture; (b) AWARE-10 architecture; (c) AWARE-40 architecture

7.2 基于分辨率提升的空间带宽积拓展

基于多探测器/多孔径合成技术为成像空间带宽积拓展提供了一种直接且可行的途径。理论上来说，只要不断提升探测器孔径数值，就能无止境地提升成像系统的空间带宽积。当然，这种堆砌硬件的做法通常被戏称为一种“土豪”式的做法[218]，不论从科研角度，还是从工程角度看，都不是一种最为理想的解决方案。而基于分辨率提升的空间带宽积拓展技术则是一种“更聪明”的做法，其仅利用单个成像系统即可一次性获得较大的成像视场（通常采用广角镜头、低倍物镜甚至无透镜光路），在此基础上，再结合之前所介绍的计算光学成像技术提升成像分辨率的方法，来实现高空间带宽积成像。

7.2.1 合成孔径全息术

相空间光学为理解数字全息的频谱分布以及对数字探测器的带宽要求提供了一个强大的工具。2013年，笔者有幸参加了于德国海德堡举办的Fringe 2013会议。在此次会议上，J. W. Goodman针对相空间光学在数字全息方面的应用作了Holography Viewed from the Perspective of the Light Field Camera的大会报告。J. W. Goodman以光场相机为类比强调了相空间光学，特别是Wigner分布函数对于分析数字全息不同记录结构的采样MTF以及像元响应非线性的重要意义[219]。图44展示了不同记录结构下的菲涅尔型全息图在维格纳空间的空间带宽积分布，图中全息图零级的空间频率为物体空间频率的两倍，这是由于物体自相关所导致的频谱展宽。相比较同轴全息图中所有信息在相空间中相互重叠，离轴全息中正负一级与零级分离，这是由于离轴参考光所引起的频率搬移所导致的。通过观察它们的相空间图可以直观看出同轴全息对于数字探测器件空间带宽积的要求要低于离轴全息，空间带宽积的有效利用率也高于离轴全息。然而由于三个级次混在一起无法分离，通常还需要用时域相移技术，以牺牲时间分辨率的方式将它们解耦。

图44 不同记录结构的菲涅尔型全息图在维格纳空间的空间带宽积表示。（a）物体的原始SBP；（b）同轴全息的SBP；（c）离轴全息的SBPFig. 44 SBP representation for different Fresnel-type holograms in Wigner space. (a) Original SBP of the object; (b) SBP for in-line geometry; and (c) SBP for off-axis geometry matching on the different elementary apertures

相比之下，离轴数字全息技术仅需采集一幅载频干涉图即可以简单高效地实现相位重建。然而由于共轭项和零频分量的存在，该方法很难充分利用成像系统与成像器件的空间带宽积。如图45所示，合成孔径全息显微技术将载频干涉条纹当作频域载波，通过频分复用原理在全息图的傅立叶频谱空间上调制多重空间信息[220]。其与众多合成孔径技术类似，也是基于移频原理。文献[221]建立了数字全息合成孔径的基本理论基础，采用倾斜照明[222]，位置扫描[223-224]等方式实现数字全息超分辨成像。成像系统可以采用共路干涉光路[225-227]，Mach-Zehnder干涉光路[228-229]，无透镜光路[223,230]，多波长复用[231]，空域最优复用策略[231-233]等。正如本文第5章所提到的，除倾斜照明外，结构光照明也是实现超分辨数字全息的常用方法[121,234]。此外，合成孔径全息显微技术不仅可以提升系统横向分辨率，同时可以提升轴向分辨率，使得系统具有高精度轴向切片能力，实现超分辨真三维成像[235,228]。值得注意的是，频分复用的原理不仅能提升分辨率，还能延展视场，可用以解决探测器靶面有限而导致的视场受限问题。其基本原理是利用物体在不同视场内信息与不同参考光角度干涉形成不同频率的载波成分，从而将看似叠加在一起的多幅空间视场信息在频谱域进行分离[236-238]。最终在频谱中分别进行解调与视场拼接，从而在不移动物体或者成像系统的前提下拓展了成像的视场，相较传统离轴全息技术，其在一定程度上提升了成像的空间带宽积。

图45 基于合成孔径的数字全息显微镜[220]。（a）合成孔径后的频谱图；（b）传统的单孔径低分辨率重建；（c）合成孔径后的高分辨率重建Fig. 45 Synthetic aperture-based digital holographic microscopy[220]. (a) Spectrum after synthetic aperture; (b) conventional single-aperture low-resolution reconstruction; (c) high-resolution reconstruction after synthetic aperture

7.2.2 傅立叶叠层显微成像

傅立叶叠层显微成像可以看作是前一节提及的合成孔径全息术的非干涉版本，该方法整合了相位恢复和合成孔径的概念，无需任何的机械移动操作，不仅可以获得与高数值孔径物镜相当的高分辨率细节，又能够保留低数值孔径物镜原有的大成像视场。典型的傅立叶叠层显微成像系统通过将传统显微镜的照明源替换为可编程LED阵列来实现，因此其可以与大多数显微镜平台兼容。可编程LED阵列可灵活调控实现角度照明扫描来记录不同空间频率的样本信息。在采集过程中，每个LED单元被顺序地点亮，产生具有一定入射角的平面波，依次照亮样品，由此记录一系列低分辨率和大视场的图像用于后续的迭代重建。其中，明场照明的子孔径光谱包含零频率分量，记录了透射光下样品的低频信息，而暗场照明将低频率分量移到所捕获的子孔径之外，收集了大角度倾斜照明下的高分辨率散射信息。通过平面照明与空间频率的一一对应关系，这些图像在傅立叶空间的相应区域采用交替投影算法被合成，显著地拓展频谱带宽，实现超越物镜衍射极限的成像分辨率。最终的等效数值孔径可以扩展为物镜数值孔径和LED阵列的照明数值孔径之和。如图46所示，傅立叶叠层显微成像技术可在2×，0.08 NA的物镜的大视场下，通过合成孔径达到了约20×物镜的成像分辨率[91]。由于其简单的硬件配置和优越的成像性能，傅立叶叠层显微成像技术已经广泛应用于生物医学和病理学领域，如疟疾感染细胞识别、循环肿瘤细胞测量和高内涵筛选等。

图46 傅立叶叠层显微成像技术采用2× 0.08 NA的物镜，在其大视场下通过合成孔径达到了约20×物镜的成像分辨率[91]Fig. 46 Fourier ptychographic microscopy uses a 2× 0.08 NA objective and achieves an imaging resolution of approximately 20× objective in its large field of view through synthetic aperture[91]

傅立叶叠层成像技术在提出伊始就引起了研究人员广泛的研究兴趣，近年来，像差补偿[239]、位置误差校正[240,109]、照明模态解耦[241-242,59]、三维衍射层析[243-245]等核心问题被相继攻克。与传统的数字全息合成孔径超分辨率算法不同，在傅立叶叠层成像交替更新算法中，相位恢复与频域合成孔径是同时完成的，这一优势也使得它可以在多个应用领域发挥强大的潜能。然而，不得不考虑的一点是，传统傅立叶叠层成像技术采用迭代重建来提升孔径带宽积的算法本质上是一个非线性优化问题，其算法收敛的关键在于原始数据约束，而这往往需要采集大量的原始低分辨率图像。这也导致了傅立叶叠层成像在生物学应用的一个最主要的问题，即成像效率较低，使其难以实现快速和动态的成像应用。针对这一问题，稀疏采样[246]、多角度照明复用[241-242]、空间分束单次采集[247-248]、差分相衬初始化迭代[93]等方法被相继提出。例如，Sun等[36,94]通过分析倾斜照明的相位传递特性，提出采用最优化的环形可编程照明来执行傅立叶叠层成像（图47），将其实现定量相位成像的数据需求量级减少，实现了动态定量相位成像。他进一步将该环形照明与颜色复用技术相结合，实现了单帧傅立叶叠层显微成像[36,94]，在1.33 mm2的视场下成像的半宽分辨率达到了388 nm，成像速度达到相机的固有帧频50 frame/s。有关傅立叶叠层成像技术的更多详细内容，感兴趣的读者可参阅相关综述论文[92,249-250]。

图47 基于环形照明的傅立叶叠层显微成像的高通量定量显微成像[36]Fig. 47 High throughput quantitative microscopic imaging based on annular illumination Fourier ptychographic microscopy[36]

7.2.3 无透镜片上显微成像

片上无透镜显微成像技术是一种无需借助任何透镜，直接将待测物体置于，或者紧靠传感器表面进行成像的高通量显微成像技术。从实现技术路线来看，其主要分为两类，即接触式投影成像技术和基于衍射的无透镜显微成像技术。在接触式投影成像中，样品紧贴传感器表面放置，使用部分相干光源直接照射相位物体，图像传感器直接采集样品的投影。不借助任何重构方法，该方法不仅能对静态物体进行成像还能对细胞分裂、运动及其他特性进行监测。2008年，Cui[251]等和Ozcan[252-253]等在微流体通道上结合片上显微技术，实现了对不同类型细胞的监测。次年，Ozcan[254]等实现了微粒和细胞强度和相位的重构。2011年，Zheng[255]等在移除相机表面玻璃的传感器表面，基于投影式无透镜显微镜实现了细胞生长以及胚胎干细胞分化的跟踪。此外，结合微流通道可有效减小实验系统体积，实现大视场高分辨成像。如2008年，Yang[251]等利用微流体、金属镀层的CMOS传感器以及微米尺寸的小孔阵列，实现了对秀丽隐杆线虫、孢子和单细胞的高分辨成像。

另一类无透镜片上显微成像技术被称为芯片上无透镜全息显微成像技术，其最初于2009年由美国加州大学洛杉矶分校（UCLA）的Ozcan课题组[256]所提出。该技术由准相干光场照射记录同轴衍射全息图，再结合相位恢复技术来减少甚至消除样品与成像面之间的衍射现象[257-259,30,260]。最初的芯片上无透镜全息显微成像技术大多是基于迭代相位复原技术，通过稀疏物体约束[256,261]或多距离强度约束恢复光场的相位分布[259,262]，再通过角谱反衍射重构出物面的强度和相位分布。2015年，本课题组[263]基于菲涅耳域内照明波长与传播距离的可置换性，将光强传输方程相位恢复技术引入到无透镜全息显微成像中，并采用“多波长照明、固定物平面”的方式避免了传统无透镜显微成像中所需引入的机械移动。与基于传统透镜的显微成像技术相比，无透镜片上显微成像技术在两个方面表现出优势[261,58]：第一，由于物体与探测器距离很小（一般小于1 mm），系统最终的成像放大率接近于1，即成像视场完全由探测器的光敏面大小所决定；第二，由于物体与探测器距离很小，成像系统的等效数值孔径也接近于1，即几乎样品的所有正向散射光均能够被探测器所接收。以上两点表明无透镜显微成像系统相当于一个放大倍数为1，数值孔径为1.0的传统光学显微系统，其空间带宽积相比于传统显微镜提升了约2个数量级。然而，由于探测器像元尺寸（通常）所导致的离散采样效应，理论的光学分辨率在实际中往往难以实现，因此迫切需要提高重构图像的分辨率。本质上而言，无透镜全息显微技术将传统的显微成像系统中的空间带宽积受限这一问题转移到了成像器件的采样率受限上。原则上说，限制芯片上无透镜全息显微技术成像分辨率的是欠采样引起的高频信号混淆失真，而非数值孔径不足引起的高频信号丢失。因此，该领域大量的研究工作都集中在“像素超分辨”上，即通过某种方式缩小等效像元尺寸，实现“亚像元成像”，从而就可以实现大数值孔径的高分辨率探测。图48（彩图见期刊电子版）显示了相关超分辨方法，包括：传感器二维横向亚像素扫描[264]、光源微位移亚像素扫描[58]、传感器轴向多离焦距离扫描[265]、照明光波长扫描[266]、基于平行板的主动光源微扫描[267]等。图49（彩图见期刊电子版）展示了基于不同无透镜成像系统的实验结果。本节的像素超分辨与第六章所讨论的图像亚像素超分辨技术在本质上是高度一致的。因为在传统像素超分辨中，水平方向的亚像素位移有助于提供额外的信息，用于消除像素混叠。而在无透镜全息显微成像中，单独使用横向位移只能消除像素混叠，而调控其余参数（如样品—传感器间距、照明角度、波长）不仅可以消除像素混叠（提高重构分辨率），还能用于消除共轭像（相位恢复）[262]，这正是Laue-Lukosz 自由度不变定理的灵活应用。有关无透镜显微成像技术更多详细内容，请参阅本课题组所撰写的综述论文《无透镜片上显微成像技术：理论、发展与应用》[57]。

图48 芯片上无透镜全息显微成像的“亚像素”超分辨技术。（a）照明源的亚像素移动[57]；（b）二维水平亚像素传感器移动[264]；（c）基于光纤阵列的光源扫描[268]；（d）照明波长扫描[266]；（e）多样品到传感器距离的轴向扫描[265]；（f）基于平行板的主动光源微扫描[267]Fig. 48 Schematic diagrams of the sub-pixel super-resolution based lensfree on-chip imaging setup. (a) Sub-pixel shifting of illumination source[57]; (b) 2D horizontal sub-pixel sensor motion[264]; (c) fiber-optic array based source scanning[268];(d) illumination wavelength scanning[266]; (e) axial scanning with multiple sample-to-sensor distances[265]; (f) active source micro-scanning using parallel plates[267]

图49 无透镜显微成像结果。（a）投影式成像系统胚胎干细胞的全场结果[255]；（b1-b9）图（a）中红框区域亚像素位移超分辨的时序结果；（c）基于多波长扫描的无透镜片上显微系统，Hela细胞的全场恢复结果[269]；（d）图（c）中Area1区域像素超分辨的时序结果Fig. 49 Lens-free microscopic imaging results. (a) Full-field results of embryonic stem cells from a projection-based imaging system[255]; (b1-b9) time-series results of subpixel shift super-resolution in the red-boxed region in (a); (c) full-field recovery results of Hela cells based on a lens-free on-chip microscopy system with multi-wavelength scanning[269];(d) time-series results of pixel super-resolution of Area1 in (c)

8 结论与展望

本文概括性地介绍了分辨率、超分辨率与空间带宽积拓展的相关基础理论，核心机理及其在计算光学成像中的若干实例。有别于大部分的综述论文与研究论文，本文所讨论的重点并不放在揭示现有方法在原理上的独特性与创造性上，也没有放在展示它们的具有吸引力的实验结果上。相反，我们将这些具体个案置入“计算光学成像”这个更高维度的体系框架去分析与探讨，在光信息论的意义上揭示了它们大多数都可以被理解为Lukosz “空间带宽积调控”策略的子集或者变体。它们本质上都是利用成像系统的可用自由度，如空间、时间、强度、相位、光谱、偏振、角动量、相干性等，在成像系统有限空间带宽积的限制下，在“得”与“失”之间所作出符合规律的权衡与选择。

本文的主要结论似乎是显而易见的，甚至可以说是微不足道的。但可以肯定的是，在当下蓬勃发展的计算光学成像这一领域中，这个结论并未得到充分的认识，或更准确地说，它未能得到足够的重视。就如同现在我们所能阅读到的大量该领域论文中，作者往往会不遗余力地在论文伊始（例如摘要）就展示出所提出的理论与方法在成像功能与性能提升方面的显著优势，却往往一直到了论文最后的结论部分都不愿意提及（不论是明确地还是隐晦地）该方法的缺点与局限性。例如针对图像像素超分辨技术，我们必须意识到并明确分辨率提升，即用于空间频率带宽提升以及解混叠，所需要的额外信息的来源。当我们利用Papoulis广义抽样原理，即采用小空间带宽积系统多帧采样来采集并重建大空间带宽积信号时，我们就必须理智地接受此过程中由于多次采样所造成的时间分辨率的损失。反之，如果只是追求最终成像指标上的“优美”而不愿意在速度、成像帧频上做出妥协，这就必须依赖于单帧图像超分辨技术。但事实上我们也必须意识到，这些额外“增长”出的图像信息的源头往往来自于先验。这就像建立了一套复杂的查找表机制，输入与输出总是由少到多的，而其中的逻辑来源于对目标场景中可能的物体特征的深入见解与精准预测，这是它们取得成功最主要的因素。当然，这类以少博多，以小博大的方法，不论是压缩感知抑或是当下非常热门的深度学习技术，都无法逾越“信息不会无中生有”，“过往不代表现在，更不能代表未来”这些既定的事实，这也预示着它们在某些“非常规”情形下失败的必然性。

因此，本文启发各位计算光学成像领域的从业者接受一些浅显易懂的光信息理论：在设计计算光学成像系统时，需要考虑图像或物体的信息量的度量，信息量经光学系统的传递，以及最后到达像平面后离散采样的影响。当采用不同光学调控或信息处理方法最大限度优化成像系统效能的同时，需要重视光学系统中传递光学信息量各自由度之间的制约关系。在光信息理论体系的指引下，借助于计算光学调控手段的灵活优势，发展求解相应逆问题的标准可重用算法，发挥成像系统有限信息资源的最大效用，针对性地在所关注的核心成像指标上实现质的突破，从而有助于面向各类复杂现实应用的新型计算成像方法更快，更系统地形成。

当然，计算光学成像现已发展为集信息光学、几何光学、计算光学、现代信号处理等理论、学科于一体的新兴交叉技术研究领域；光学信息论也是一门广泛涉及光学、概率论、量子理论、数学物理方法、通信原理等学科的综合学科。它们之间的深入交融以及在有关分辨率、超分辨率与空间带宽积拓展方面的进一步应用，还需要借助于各种类型的光学成像技术与系统来说明。由于本文篇幅所限，无法对此方面全面涉及。以下列出了笔者在本文未重点阐述但又十分重要的研究方向，这里仅做简要提及。

8.1 光学传递函数调控

在第二章中，我们讨论了光学传递函数与成像系统的性能紧密相关，其截止频率决定了成像分辨率，其响应幅度决定了成像的对比度与信噪比。Lukosz超分辨思想主要揭示了给定成像系统下信道容量与视场、空间带宽间的制约关系。但值得注意的是，计算光学成像系统的信道容量是与其采用的光学调控机制紧密相关的，而光学传递函数的截止频率与信噪比（即与坐标轴所围成的面积）在一定程度上反应了信道容量，因此可以通过光学传递函数调控的方式提升成像分辨率与信噪比，这点在基于相空间光学的成像系统分析中表现的更为清晰。以定量相位成像为例，如果采用非相干光场照明，由于光学传递函数的虚部为0（没有相位衬度），无法对相位信息进行成像[43,28]。这也就意味着该成像系统其对相位信息传递的信道容量为0，显然与对吸收物体成像的情况截然不同。而基于计算光学成像的思想，可通过照明调制[270]、孔径函数调制[271]等方式有效地针对相位信息传递，最大化相位传递函数的响应幅度与截止频率。例如最近我们的研究表明，匹配物镜数值孔径的环形照明非常适于对相位信息成像与探测，它不仅可以提供较高的成像衬度（MTF平坦且幅值较高），还可将非干涉定量相位成像的分辨率拓展到非相干衍射极限（截止频率达到fincoh）[28,272,36,34]。当然在此过程中，我们也需要对成像系统的光能利用率做出一定的妥协（环形照明总能量低于圆形照明孔径，因为其只是圆形照明孔径的一个子集），但这正体现了计算光学成像中“Less is more”（笔者这里将其翻译为有无相生）的哲学思想。

8.2 频谱外推与信息分辨率

由阿贝成像理论推演得到的阿贝衍射极限虽然在物理上看是严密的，但其成立的条件是基于空域无限的周期光栅的图像所推演得到的。然而，如果物体是一个有限尺度的光栅，其衍射的阶次就会额外衍生出许多高阶项，这些边带信息可能会落入物镜的数值孔径之中，从而为其信号反演提供了可能。显然，由观测图像和成像系统的PSF或者OTF的信息恢复原始高分辨率图像本质上是数学上的病态逆问题。其与相位恢复问题本质上非常类似，可以借助于Gerchberg-Papoulis (GP)[273]、Gerchberg-Saxton（GS）[274-275]或 者Fienup Hybrid Input-Output（HIO）[30]这类在傅立叶域与空间域进行反复投影的算法进行迭代优化求解。

本文第6章所讨论的压缩采样理论表明，在满足稀疏性与非相干性条件下，可以通过远少于传统香农-奈奎斯特采样的数据来恢复原信号。Donoho等[276]从数学角度深入阐述了这个问题，其主要结论是当一个物体如果在空域是稀疏的，即其共计n个采样点中有m/2个为0（m/2≤n）（Donoho等将其称为nearly black条件），其可以仅用一部分（n个其中的m个）的傅立叶系数对其进行完美重建。将该理论应用到成像系统，这一部分傅立叶系数必须能落入物镜的数值孔径之中，以此来推演衍射极限以外的高频分量，如图50通过有限区间频谱信息外推整个信号所示。该思想又被称为解析延拓理论，即任何空域有界函数的频谱函数是解析函数，因此只要能准确地知道它在有限区间内的部分信息就可以唯一确定整个函数。而基于此方法的超分辨技术称为解析延拓或频谱外推[277-278]，其对分辨率提升的有效性已经在相位恢复[279]、图像复原[280]、数字全息[281-282]等领域得到广泛的验证与应用。该思想其实也隐含在了Lukosz超分辨方案中，以牺牲一半的视场来换取2倍分辨率的提升。虽然解析延拓理论在理论上是完备的，但实际应用中所能达到的分辨率极易受到噪声与其他干扰信号的影响，这也从一定程度上反映了以香农信息论为基础，以信噪比为核心所定义的成像系统的“信息分辨率”极限[283-284]。

图50 通过有限区间频谱信息外推整个信号Fig. 50 Extrapolation of the entire signal through finite interval spectrum information

8.3 三维层析中的合成孔径

本文所讨论的光学成像技术着重针对二维成像，因此本文所指的分辨率特指横向分辨率。而在实际应用中，样品往往不仅仅局限在二维平面。事实上，生命有机体，大到人体小到组成人体的每个细胞，都是具有一定内部结构的三维物体。为了获得样品三维空间的立体结构，必须借助于断层扫描技术或者层析成像技术。X射线断层扫描术（X-ray CT）与核磁共振成像（Magnetic Resonance Imaging，MRI）是当今医学影像学中最为重要的三维成像技术，它们都是基于Radon所提出的投影重建理论（傅立叶切片定量）[285]。将该理论应用于光学波段或较小尺度的样品，就必须考虑光波的衍射效应，即需要借助于Wolf的衍射层析理论[286]。本质上而言，它们都可以被认为是一种合成孔径技术，只不过将二维频谱空间拓展

到了三维。例如基于衍射层析显微成像技术往往需要通过旋转物体[287-288]，改变照明方向[228,235,289-290]等方式得到各角度散射场的复振幅信息，然后在一阶Born或Rytov近似下对物体三维散射势频谱填充与合成孔径[26]。类似地，结构光照明显微成像也可以被拓展到三维成像（3D-SIM），其在2D-SIM的双光束干涉的基础上再加一束干涉光以产生轴向驻波效应，进而提升轴向层析分辨率[291]。值得注意的是，这些技术与二维合成孔径类似，在传递函数优化[292]、非干涉叠层重建[45,245]、频谱复用解耦[293-294]等方面也都取得了诸多成效，但最终仍需要在成像系统有限空间带宽积的限制下，在成像分辨率、成像速度与视场之间做出权衡。此外，此类技术还普遍面临由于照明与探测孔径角受限所致的“频谱缺失锥”这一共性问题。该问题可以通过引入目标分布的先验信息（如非负性、分片平滑性），并基于上小节提到频谱外推以及正则化方法加以补偿[295]。

8.4 近场显微与倏逝波收集

目前大部分计算光学成像技术所考虑的衍射极限仅仅限于传输波，倏逝波并没有被纳入其中。Lukosz的原始工作也并没有考虑倏逝波与超分辨之间的关系。当然，最直接的对束缚在样品表面含有高空间频率倏逝波进行收集的方式是采用扫描近场光学显微术（Scanning Near-field Optical Microscope，SNOM）[296]，利用纳米尺度探针将样品表面位置的倏逝波成分耦合成远场区域可以探测的行波，其广泛地应用于光学、化学、材料和生物等领域中。但它仍存在一些不足，如光学探针的加工要求与精度较高，且需要高精度的近场操作手段作为保障。为了解决这个问题，可以借助于计算光学成像中的合成孔径技术思想，通过光场调制将传统光学显微镜无法获取到的样品高频分量移动到系统的低通频带范围内。随后通过频谱解调，实现频谱接收范围的有效扩展[297]。为了实现有效的倏逝波频率搬移，通常需要借助于介质材料全反射产生的倏逝波和金属介质界面产生的表面等离激元。如图51所示，这些技术在本质思想上与本文第五章讨论的传统合成孔径技术，如结构光照明[298-299]与傅立叶叠层成像[300]技术十分类似，因此完全也可以被囊括在Lukosz超分辨框架中。

图51 传统SIM和基于表面等离激元PSIM原理示意图[298]。 （a）SIM；（b）PSIM；（c）介质中传播的色散曲线示意图Fig. 51 Illustration of the SIM and PSIM principles[298]. (a) SIM; (b) PSIM; (c) schematic of the dispersion curves of the propagating photon in dielectric media

8.5 基于深度学习的超分辨成像

深度学习作为近年来兴起的一种“数据驱动”技术，在光学成像领域受到越来越多的关注，并在近几年取得了丰硕的成果。它颠覆了传统计算成像的“物理模型驱动”方式，并开启了基于“数据驱动”的新范式[301-303]。对比传统方法的正则化函数或指定先验，深度学习所学习到的先验信息是针对真实实验数据的统计量身定制的，这原则上为求解反问题提供了更强、更合理的正则化。因此其绕过了求解非线性病态逆问题的障碍，可以直接建立输入与期望输出之间的伪逆映射关系。大量已发表的文献结果表明，基于深度学习的超分辨成像技术能够在极小的数据量需求下，提供显著优于基于先验或物理模型的传统的计算成像方法的性能[304-305,167,306]。但就如同本章开头所述，由于信息并不会“无中生有”，深度学习所获得的结果不可能总是准确可靠的。深度学习的成功通常取决于从训练样本中学习和提取的“共同”特征作为先验信息。因此当面对“罕见样本”时，人工神经网络是无法保证其结果的准确性的。

最后，不论是Lukosz空间带宽积调控，还是Papoulis广义采样，其本质上就是Laue-Lukosz 自由度不变定理背后思想的集中体现——想要在“分辨率”上有所“得”，就必须在另一个光学自由度上，如成像视场、时间分辨率、光谱分辨率等，有所“失”。它们实质上都是在物理限制下，在“得”与“失”之间所作出的符合规律的权衡与选择。“得”与“失”背后反映的是一种哲学思想，就如同中国从古到今观念中的阴阳、天地、五行一样，相辅相成，相生相剋，是一种既对立又统一的矛盾体。这或许也能够留给我们一丝人生启发：因为实无所“舍”，亦无所“得”，何不视“失”为“舍”，以“舍”博“得”。

致谢：南京理工大学智能计算成像实验室的张润南、钱佳铭、王博文、胡岩、卢林芃、范瑶、李加基、李卓识、吴雪娟等在本文的图表绘制、内容完善以及文字校对过程中做出了大量工作，在此向他们深表谢意。