蚁群算法在辅助导航重力匹配中的应用

陈小炜， 姜广胜， 陈 静

(陆军步兵学院石家庄校区军政训练系，石家庄，050083)

卫星导航虽然精度高，适用范围广，但对于水下潜器以及需要隐身的装备而言，惯性导航才是最佳选择。惯性导航基于惯性元器件解算出自身位置和姿态，不向外辐射信号，因此隐蔽性好，实用性强，但其是一种基于位推算法的定位方式，误差会随时间积累，长时间导航将无法满足定位需求，需要外部信息进行校对。由于重力异常容易获取，通过重力场特征信号获取位置信息，反馈给惯导系统进行位置误差校对，依然能够维持惯导系统的隐蔽性和自主性，所以重力匹配仍具备不受外界干扰等优点[1]。经典的重力匹配方法分为递推最优估计滤波和相关值匹配。近几年，相关值匹配取得了很大突破，产生很多研究成果，包括神经网络、支持向量机、数据关联滤波等[2-3]。蚁群算法是一种群智能最优搜索算法[4-6]，王晓燕等[7]结合蚁群算法与人工势场法，给不同的栅格位置赋予不同的初始信息素，通过不同信息素浓度，加速蚁群收敛速度，提高算法的搜索效率。敖邦乾等[8]使用Dubins曲线算法和贝塞尔三阶曲线理论，对水面无人艇路径的连接点与路径进行平滑处理，使路径在满足最小旋转半径的同时也满足动力学特性。本文将蚁群算法应用到重力匹配中，并将速度信息作为约束条件，同时根据搜索策略对蚁群算法的信息素浓度、算法参数进行自适应调整，并与均方差算法进行匹配，通过两种算法仿真数据对比，验证蚁群算法是否提高了匹配的搜索效率和匹配率。

1 蚁群算法

研究者发现蚂蚁会在所经过的路径上释放出一种特殊的激素，为其他蚂蚁提供方向指引，学者们称这种特殊的激素为信息素。信息素的浓度会随着时间产生挥发，所以路径越长，信息素浓度就越低，被其他蚂蚁察觉的概率就越小；相反，路径越短，信息素浓度就高，就会有更多蚂蚁选择该路径。蚂蚁越多，信息素的浓度就会不断加强；蚂蚁越少，信息素浓度就难以维持，直至最后因缺少信息素而被遗弃。因此形成了一种基于信息素浓度的正反馈机制，通过信息素浓度的变化来找到一条最优路径。蚁群算法的特性使得它非常适用于组合优化问题，通过信息素浓度来确定最优解，并且取得了良好的效果。蚁群算法一般包括参数初始化、循环遍历、信息素更新、判断是否终止等环节，见图1。

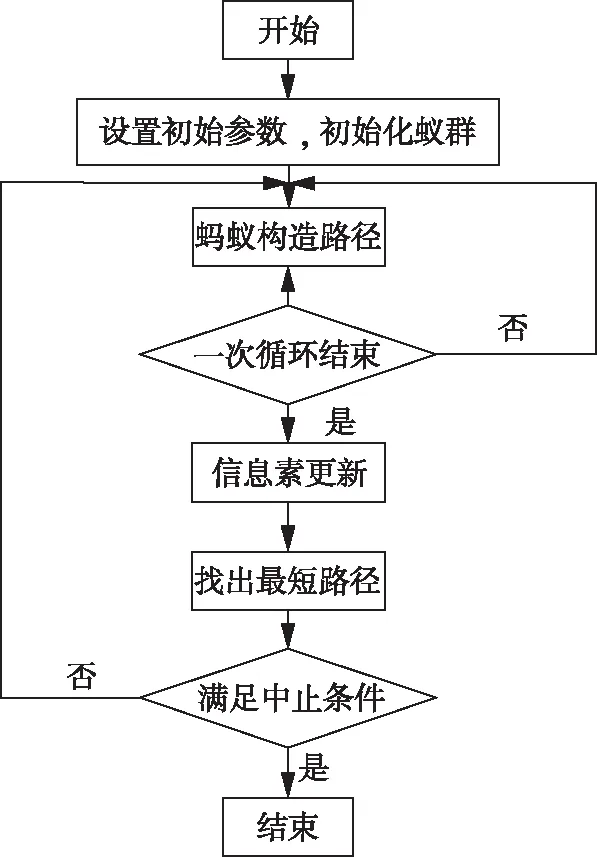
图1 蚁群算法流程图

设C={c1,c2,…,cn}为n个节点集合，L={lij|ci,cj∈C}是C集合中不同节点间的路径权值集合。τij(t)是信息素浓度值，表示t时刻路径(i,j)上残留的信息留浓度。Γ={τij(t)|ci,cj∈C}是τij(t)的集合，t=0时，各路径上的信息素浓度初始值相等，τij(0)=const。通过(C,L,Γ)集合组合蚁群算法的有向图，通过有向图G=(C,L,Γ)能够实现蚁群算法，获得最优解。

(1)

式中：α为信息启发因子，表示信息素对于蚂蚁选择该路径影响大小，α越大，影响越大，群体之间协作性越强；ηij(t)为启发函数，表示在t时刻蚂蚁从i转移到j的期望程度，代表了蚂蚁的主观性；β为期望启发因子，表示启发函数对于路径选择的重要性，β值越大，表示蚂蚁选择主观性更强，更接近于贪心规则；allowedk(i)代表了蚂蚁k的可选择集合，即位于节点i上的蚂蚁在进行下一步转移是可以到达的节点集合。

信息素浓度与启发信息都对转移概率有很大影响，且两者是对立的。所以，在搜索过程中要不断进行更新，防止信息素和启发信息数值相差过大，淹没对方。t+n时刻在路径(i,j)上的信息素更新如下：

(2)

式中：ρ为信息素挥发因子，(1-ρ)则为信息素残留因子，其中ρ∈(0,1)；Δτij(t)为t时刻路径(i,j)信息素量的增量，其中Δτij(0)=0。

2 重力匹配相关方法

重力信息实时测量和重力场背景图测绘能力是重力匹配的基础[9-11]。重力匹配是将航迹上的重力测量值与参考重力进行运算，通过求取极值或最优解来确定对应的位置信息。

匹配分为粗匹配和精匹配，分别对应搜索模式和跟踪模式。初始匹配是在搜索模式下进行的，此时惯导因误差较大需要校对，借助惯导系统可以确定载体的大致范围，同时根据重力基准图确定匹配范围。此时系统进入跟踪模式，通过载体轨迹上的测量值确定载体的真实位置。

因为惯导系统误差过大，所以在搜索模式下，需要扩大搜索范围，因此匹配范围也较大，保证载体真实位置在匹配范围内。此时需要载体采集一定的重力数据，通过连续的测量值确定载体的粗略位置。

进入跟踪模式后，载体将搜索模式得到的位置作为已知位置，从该位置出发，间隔固定时间沿某一方向进行采样，记录该时刻对应的重力测量值。最后将惯导指示航迹和载体行进过程中的的真实轨迹记录到重力图上，如图2所示。其中Ai表示载体在ti时刻的真实位置，Ci是该时刻惯导平台输出的位置。gi是重力仪在该时刻的测量值，也就是Ai处的重力值。因此存在3个点集：

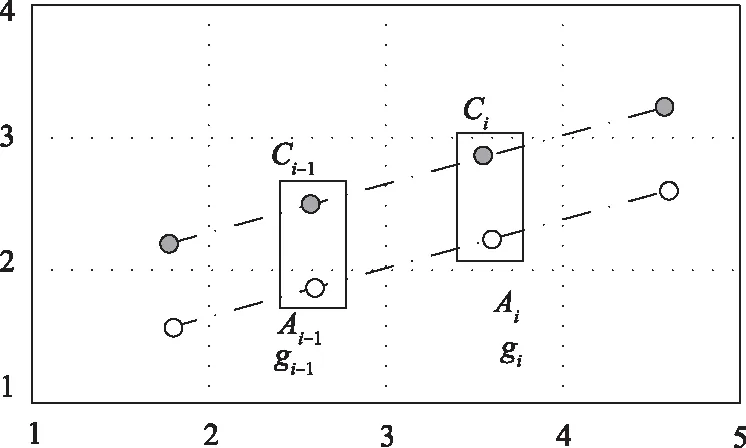
图2 真实航迹与INS指示航迹关系

A={Ai},C={Ci},G={gi},i=0,1,…,m

载体航迹重力测量值由点集C构成，点集A是载体的真实轨迹。本文将通过点集C和点集G，依据蚁群算法找到点集A。

根据测量位置，将搜索区域栅格化。将测量点Ci作为搜索中心，以距离Ri为搜索半径，在重力图划分网格点搜索区域，Ri要确保网格区域应包含Ai，也就是载体对应的真实位置。在网格范围内搜索测量值gi的等值点，搜索范围以Ci为中心向外辐射，其中dij表示搜索范围内测量值gi的第j个等值点，标记为网格点。半径Ri根据惯性单元的漂移误差来确定，惯性元件导航时间越长，精度就越低，半径也越大，同时Ri要考虑重力异常对惯性导航系统定位精度的影响[12-13]。dij的对应经纬度坐标为(λij,φij)，通过基准数据库获取该地理位置的重力值为gij，Ci的地理经纬度为(λci,φci)，Ri的单位为网格数，网格之间的距离为ρ。所以，等值点集Di可以由式(3)确定：

(3)

i=0,1,…,m;j=1,2,…,Ni

式中：Di为等值点集合，Ni为点数，δ为等值点的误差阈值，在该阈值范围内视为等值点。

3 匹配算法

3.1 相关值搜索匹配

根据惯性导航输出的位置，通过搜索查询基准重力数据库，可以得到对应的重力异常值g'N=[g'1,g'2,…,g'N]。通过重力仪或重力梯度仪可以测得载体航迹上的重力异常值gN=[g1,g2,…,gN]。搜索模式下，根据惯性元件的误差及位置信息确定搜索区域，也就是匹配区域。为保证实际航迹在搜索区域内，在不牺牲收敛速度的前提下，尽量扩大搜索范围。以短时间内航迹作为实验数据，只要时间足够短，便可得到与实际轨迹相平行的惯导输出轨迹。在搜索区域，可以得到S个与惯导输出轨迹平行的轨迹簇，假设平行轨迹簇中有S个轨迹，在重力数据库中提取重力异常值，得到S个数据向量。把重力仪测量值向量和数据库中提取的数据向量进行相关极值运算，可以确定航行体的位置。本文相关极值匹配算法选用常用的均方误差(MSD)算法，把搜索区域中得到的S个数据向量与观测值向量分别按式(4)计算均方误差JMSD, 最小的JMSD对应的即为匹配位置。

(4)

式中：k=1,2,…,N。

3.2 蚁群搜索匹配

当蚂蚁从起点到终点遍历完所有点，该集合便是一条匹配路径。如果蚂蚁到达某一节点，而该节点无法进行到下一节点，也是一次完整的遍历，即是匹配中的一个解，当足够数量的蚂蚁走完所有可能的路径，便包含了最优解。

节点D0为已知点，当蚂蚁从D0到达D1时有N1(N1为点集D1中等值点数)条有向线段。当蚂蚁从D1到达D2时，根据自由组合的可能路线，便形成N1×N2条路线。所以，以此类推，蚂蚁从Di到Di+1有Ni×Ni+1条路线。α[i,j]为每只蚂蚁从i到i+1选择的有向线段(j=1,2,…,Ni×Ni+1)。蚂蚁遍历的所有路径中，只有一条路径与真实路径最接近，以此作为目标函数，并通过速度信息进行约束，便能找到蚁群搜索路径得到最优解。

实验中通过多普勒测速仪等设备可以获得作为外部约束条件的速度信息，以此建立的目标函数为：

s.t.x=(x1j,x2j,…,xnj)∈S⊆D

(5)

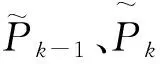
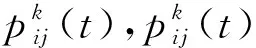
蚂蚁k在选择路径前往下一节点时，如果点集D中没有满足约束条件的节点，则蚂蚁k将自动死亡，也就是完成了一些遍历。蚂蚁k死亡后，更新禁忌表tabuk中的数字为{1,2,…,i,…}，禁忌表代表蚂蚁完成的遍历，且{1,2,…,i,…}⊆{1,2,…,n}，则蚂蚁k得到的解为：

Lk=|‖αij-α1j‖-vt|

(6)

当m只蚂蚁都完成遍历后，禁忌表更新完成，此时根据矩阵方程，可求得m组可行解。本次遍历取得的最优解优于当前解的话，则将本次最优解作为当前最优解。如果遍历次数小于最大循环次数，根据式(1)～(2)更新路径上的信息素，并进入下一次搜索。如果遍历次数大于或等于最大循环次数，则遍历结束，当前最优解即最终解。

4 仿真结果与分析

本文模拟生成惯性导航系统轨迹包括INS指示轨迹和载体真实轨迹。为了能够验证算法有效性，提前设定一条位置已知的轨迹，作为理论轨迹。惯导系统输出的轨迹是根据惯导仿真模型获得的轨迹，通过与真实惯导对比，该模型参数符合实际要求。取经度为125°～126.5°，纬度为45°～ 45.6°，高程为水平面组成的面内的所有重力异常数据。重力异常数据是由EGM2008重力异常数据库生成，分布图见图3。根据提前设定，将载体的航迹预设在该区域内，惯导系统的仿真数据就是按照提前设定轨迹进行仿真，从而得到该轨迹上INS指示轨迹。

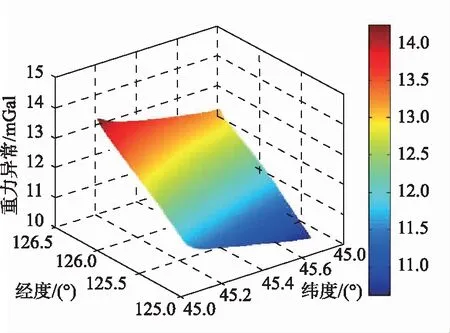
图3 重力异常曲面图

在搜索模式下，通过式(3)计算获取重力异常测量值的等值点，将等值点作为蚁群遍历节点，根据表1的参数进行设置仿真计算。实验中采用的惯导数据模型为光纤陀螺的参数，误差包含初始位置误差、常值漂移和随机噪声3种。其中，通过转台实验测得设备的常值漂移误差为0.01°/h，随机噪声均值为0，标准差为0.001的高斯分布白噪声。重力仪的实时量测数据是利用真实航迹在重力数据库中的采样值加上一定的测量噪声得到的。蚁群算法的参数设置见表1。

表1 蚁群算法参数设置

对蚁群算法进行仿真，得到匹配最优解。同时通过MSD算法进行仿真，并对两种算法仿真结果进行对比。图4惯导输出航迹、理论航迹、MSD匹配算法仿真航迹和蚁群匹配算法仿真航迹。图5为不同算法匹配的误差图。

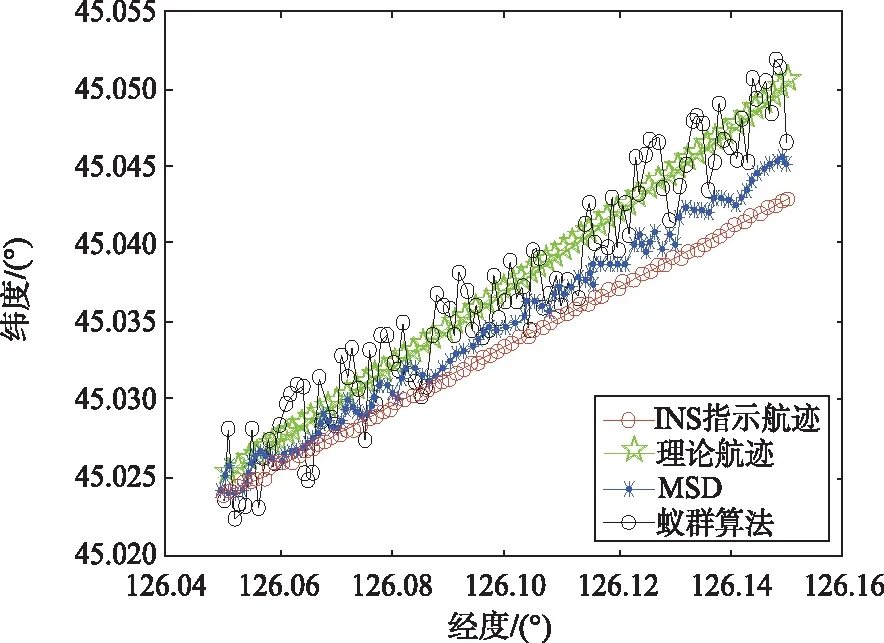
图4 航迹轨迹仿真图

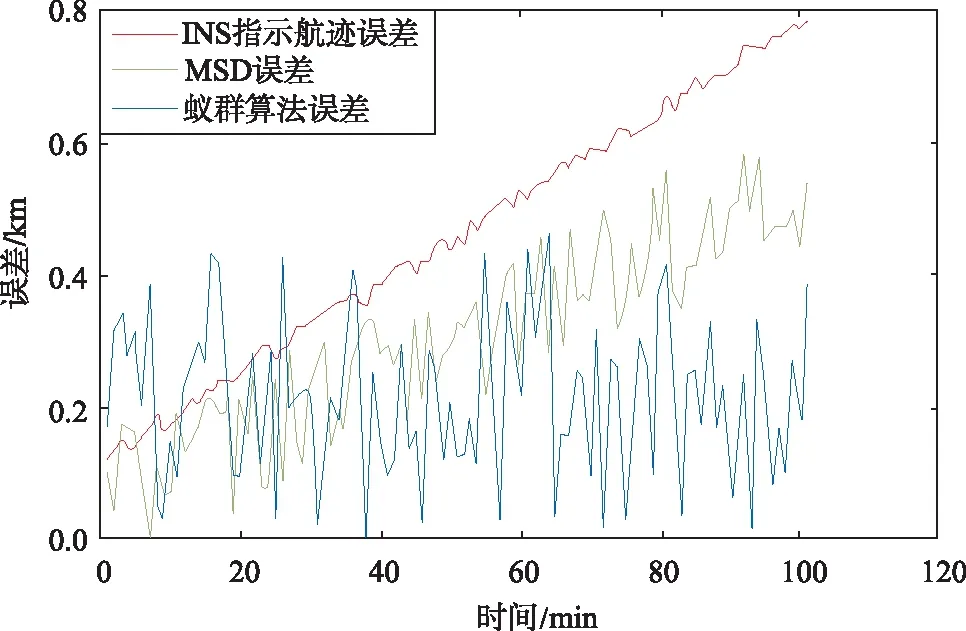
图5 匹配误差图

从图4和图5能够看出，惯导误差呈发散趋势，而MSD算法和蚁群误差相对稳定，且匹配效果优于惯导输出轨迹。表2为通过蚁群算法和MSD算法获得的匹配精度。从结果可以看出，相比于MSD算法，蚁群搜索算法误差均值更小，更加平稳，匹配精度更高，匹配效果更好。

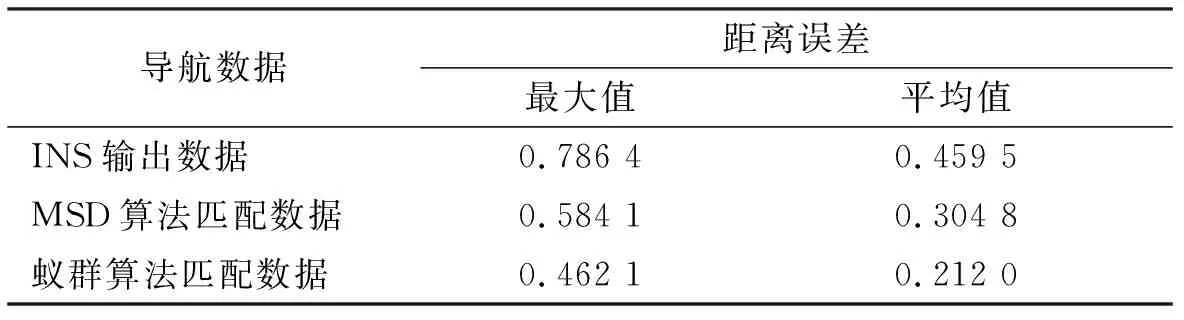
表2 经纬度误差 单位：km

5 结语

本文探索了基于蚁群算法的重力匹配，并建立仿真环境对该算法进行测试，将蚁群算法与相关极值算法中的MSD算法进行对比分析。仿真结果表明，蚁群算法匹配精度更高，能够找到一条更接近真实航迹的路线，有效避免误匹配的情况。