基于数据融合与GRU的航空发动机剩余寿命预测

2023-01-07李路云王海瑞朱贵富

空军工程大学学报 2022年6期

李路云，王海瑞，朱贵富

(1.昆明理工大学信息工程与自动化学院，昆明，650500；2.昆明理工大学信息化建设管理中心，昆明，650500)

航空发动机是飞机的核心部件，它的健康状况关系到飞机的安全性与经济性，对它进行准确合理的预测性维护就相当重要。利用传感器采集技术和先进智能技术对发动机的剩余寿命进行预测,就成了预测性维护工作中的关键一环。

随着“大数据”时代的到来，数据驱动的方法逐渐成为剩余寿命预测的主流方法[1]。任子强等将多源传感器数据融合成一维复合健康指标，再利用线性Wiener过程对一维复合健康指标进行退化建模[2]。虽然随机退化模型有较强的可解释性，但预测精度还有待提高。Li等采用SFS算法优化了SVR中的超参数，实现了滚动轴承的剩余寿命预测[3]。浅层机器学习难以充分提取设备的退化特征，在预测准确性和鲁棒性方面，深度学习更具优势[4]。为获得更高的预测精度，马忠等利用改进的CNN对航空发动机的剩余寿命进行预测[5]。Kong等提出了一种DCNN与LSTM相结合的方法，同时使用贝叶斯优化算法对两个网络的超参数进行优化，有效提高了锂离子电池的剩余寿命预测精度[6]。以上方法虽然获得了较好的预测效果，但并未对预测中的不确定性进行量化。航空发动机工作环境复杂，采集到的退化数据不可避免地会受到噪声的污染，为使预测结果更接近现实，应对预测中的不确定性进行量化[7]。Sun等将MC Dropout技术应用于多尺度卷积神经网络中，实现了滚动轴承剩余寿命的区间预测[8]。该方法有效量化了滚动轴承剩余寿命预测中的不确定性，但这种不确定性依赖于网络结构，无法保证预测结果的可靠性。李浩等利用SAE构造健康指标，将提取后的健康指标放入基于BiLSTM构建的DeepAR模型中进行剩余寿命预测[9]。该方法实现了发动机剩余寿命的区间预测，但是通过SAE构造的健康指标依然存在可解释性差的弊端。

利用深度学习进行寿命预测可获得较高的预测精度，但通过模型构造的健康指标和模型的可解释性成了一个巨大的挑战[10]。数理统计的方法可解释性强，但处理大数据的能力还有待提高。于是，专家们开始提出一种将深度学习与数理统计相结合的剩余寿命预测方法。Liu等利用PCA提取隐藏在原始传感器数据中的关键特征，再构建一个由Wiener 过程、LSTM、XGBoost等构成的动态多阶段组合预测模型实现对航空发动机的剩余寿命预测[11]。彭开香等采用DBN构造健康指标，再利用HMM模型实现对航空发动机的剩余寿命预测[12]。以上两种方法结合了深度学习和数理统计两者的优点，互相弥补彼此的不足，但这样的结合仍然存在两大缺陷：一是利用深度学习模型构造的健康指标可解释性差；二是提取的健康指标和随机模型是否匹配也是一个需要解决的问题[13]。

基于以上分析，本文提出一种融合数理统计与深度学习的新型航空发动机剩余寿命预测方法。一方面，利用Wiener过程建立退化模型，将模型预测寿命和真实寿命之间的偏差作为优化目标函数，形成复合健康指标提取与随机退化建模的反馈闭环，经过多次优化调整得到融合系数的最优解，再利用融合系数的最优解将多源传感器数据进行加权融合，构造一个解释性强的一维复合健康指标[13]。另一方面，利用一维复合健康指标和Bootstrap方法构建n个基于GRU的集成回归模型和1个基于GRU的预测误差模型，最终得到航空发动机剩余寿命的区间预测，有效解决了深度学习模型中预测结果不确定性难以量化的问题，为实际工程问题提供了一种新的解决思路。

1 理论基础

1.1 健康指标的构造

航空发动机是一种复杂的大型机械设备，仅依靠单一传感器监测数据并不能全面有效地表征发动机的健康状态，需要将多源传感器监测数据进行融合，充分提取所有监测数据中的退化特征，从而准确预测发动机的剩余寿命[14]。本实验选用的训练集包含100个发动机从开始运行至失效的完整状态数据，测试集包含100个发动机失效前某一段时间内的非完整监测数据。每个发动机的退化数据都是由21维传感器监测得到的，这些退化数据具有大规模、高维度、非完整的特点。为充分提取所有监测数据中的退化特征，本文参考和借鉴文献[13]的方法，将能够体现发动机退化趋势的14维传感器数据进行加权融合，构造一个可解释性强的健康指标。

1.1.1 多源传感器数据加权融合

利用式(1)构造一维复合健康指标：

(1)

式中：S为传感器的个数；ωb为第b个传感器数据的融合系数；xm,b(t)表示第m个发动机的第b个传感器在t时刻采集到的退化数据。

第m个发动机对应的监测时间记作tm，则复合健康指标对应的观测数据记作fm，如式(2)、式(3)所示。

tm={tm,0,tm,1,tm,2,…,tm,Km}

(2)

fm={fm,0,fm,1,fm,2,…,fm,km}

(3)

式中：fm,k=Fm(tm,k)，k=0,1,2,…,Km;Km为第m个发动机的监测数据个数，Δt=tm,k-tm,k-1。

1.1.2 利用Wiener过程退化建模

利用线性Wiener过程对复合健康指标进行建模。模型描述如下：

Fm(t)=fm,0+λmt+σmB(t)

(4)

式中：fm,0为第m个发动机在tm,0=0时刻的初始退化量；λm为漂移系数，反应了第m个发动机的退化率；σm为第m个发动机的扩散系数，刻画退化过程的随机不确定性；B(t)为反映退化过程时变随机性的标准Brownian运动。

1.1.3 求解融合系数

构建如下式所示表征预测效果的优化目标函数：

(5)

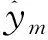
{W*,ν*}=minJ(W,ν)

(6)

通过最小化J(W,ν)可得到最优解{W*,ν*},本文利用拟牛顿法对式(6)进行多维搜索求解，具体求解过程如图1所示。

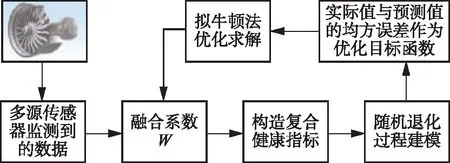
图1 多源传感器数据融合过程

1.1.4 健康指标的评估

为证明加权融合方法构造的健康指标优于其他方法构造的健康指标，本文采用Spearman相关系数评估发动机剩余寿命与健康指标之间的关联程度。Spearman相关系数的绝对值越大，两变量之间的关联程度越强[15]，Spearman相关系数的计算公式如下：

(7)

1.2 基于GRU和Bootstrap方法的剩余寿命预测

GRU网络运行速度快、处理时序特征有较好的优势，但无法量化寿命预测的不确定性，于是将它与Bootstrap方法进行结合，通过Bootstrap方法对最优复合健康指标进行重复抽样来量化寿命预测的不确定性。与其他预测模型相比，这种组合方法不仅能获得较高的预测精度，还能实现对航空发动机剩余寿命的单点预测和区间预测。

1.2.1 Bootstrap方法

Bootstrap是一种通过对传感器监测数据进行重复抽样来量化预测不确定性的方法，其基本思想是通过对原始样本进行n次有放回抽样，得到n个与原始样本大小相等的Bootstrap样本[16]。Bootstrap方法从理论上减少了预测值与真实值之间的偏差，适用于难于获取区间估计的样本预测[17]。

1.2.2 GRU

GRU[18]和LSTM[19]一样，是为了解决RNN梯度消失问题而提出来的。GRU与LSTM的区别主要在于GRU的结构和参数比LSTM更简单，运算效率更高效，GRU的结构如图2所示，主要由重置门和更新门构成。

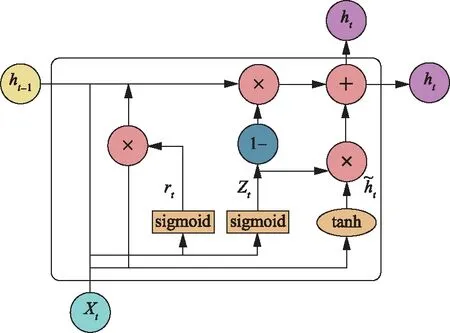
图2 GRU的结构图

计算公式如下：

(8)

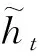
1.2.3 构建GRU和Bootstrap方法的寿命预测模型

文献[20]利用Bootstrap方法和二维DCNN实现了对滚动轴承的剩余寿命区间预测，本文参考此文献方法，利用GRU和Bootstrap方法实现对航空发动机的剩余寿命区间预测(图3)。

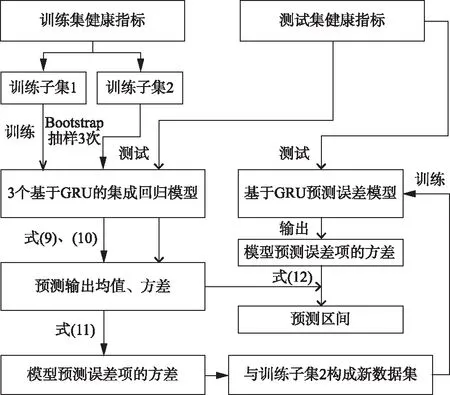
图3 Bootstrap-GRU预测模型

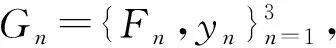
步骤4利用Gn中的3个Bootstrap样本分别训练3个基于GRU的集成回归模型。

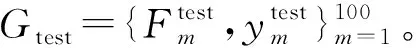
(9)

(10)

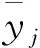
步骤8采用式(11)近似求出模型预测误差项的方差。

(11)

步骤10构建一个新的基于GRU的预测误差模型完成对新数据集Gr2的训练。

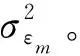
(12)

2 方法步骤

为解决深度学习方法在航空发动机剩余寿命预测中存在的弊端，提出一种多源传感器数据加权融合与GRU相结合的剩余寿命预测方法。其核心步骤是：①通过直接观察法挑选出能够表征发动机退化趋势的14维传感器监测数据作为特征参数，对特征参数进行标准化和贴标签处理；②利用Wiener过程构建一个反馈闭环回路，通过对优化目标函数进行搜索寻优，得到多源传感器数据的融合系数，根据融合系数构造一维复合健康指标；③利用一维复合健康指标和Bootstrap方法构建3个基于GRU网络的集成回归模型和一个基于GRU网络的预测误差模型，根据模型预测结果计算得到发动机剩余寿命的预测区间；④采用均方根误差和评分函数对预测结果进行评价。具体实施流程如图4所示。

图4 方法流程图

3 实验研究与分析

3.1 实验数据

为验证本文所提方法的效果，选取C-MAPSS涡扇发动机退化数据集中的FD0001数据集进行实验，该数据集包含训练集、测试集，具体数据信息如表1所示[21]。

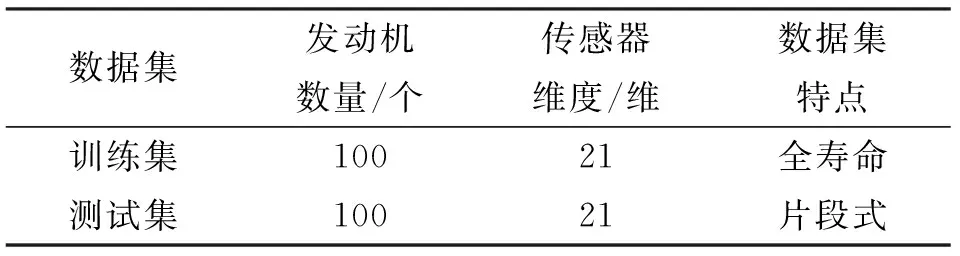
表1 FD0001数据集

3.2 性能度量指标

本文选用均方根误差和评分函数作为模型的性能度量指标[22]。

均方根误差(RMSE，式中简记RRMSE)的数学表达为：

(13)

评分函数(Score，式中简记Sscore)表达式如式(14)、式(15)所示：

(14)

(15)

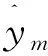
图5 评价函数图像

3.3 数据预处理

训练集中1号发动机的21维传感器监测到的数据如图6所示，从图6中可以看出，2、3、4、7、8、9、11、12、13、14、15、17、20、21号传感器监测到的数据能够反映涡扇发动机的退化趋势，因此选择以上14维传感器监测到的数据作为模型的特征参数。

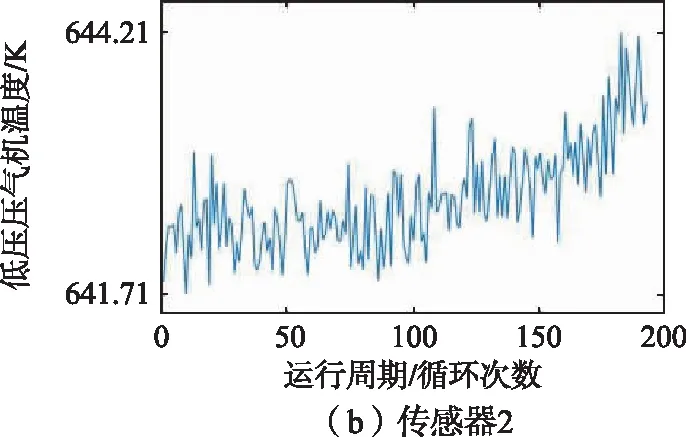
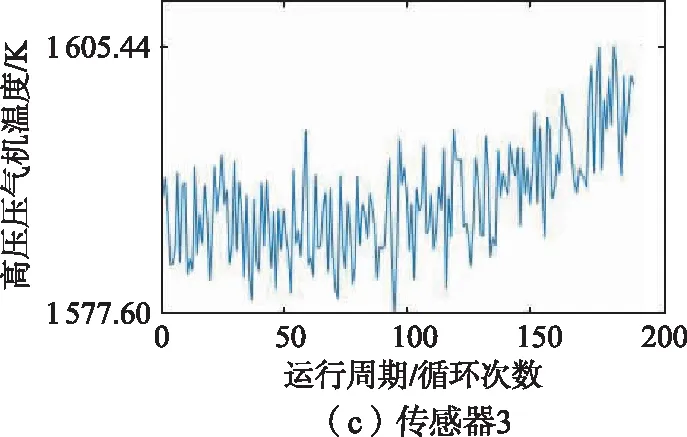
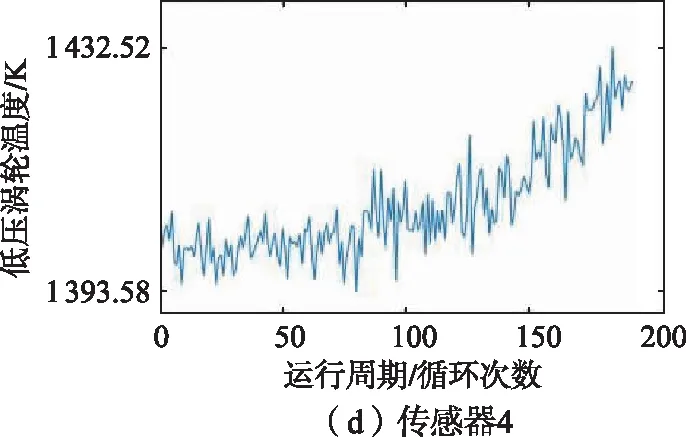
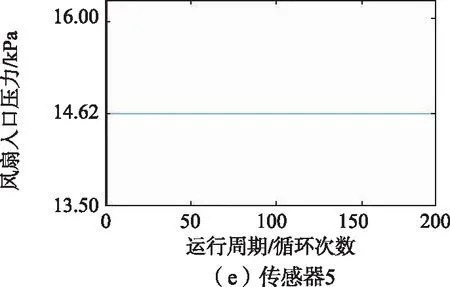
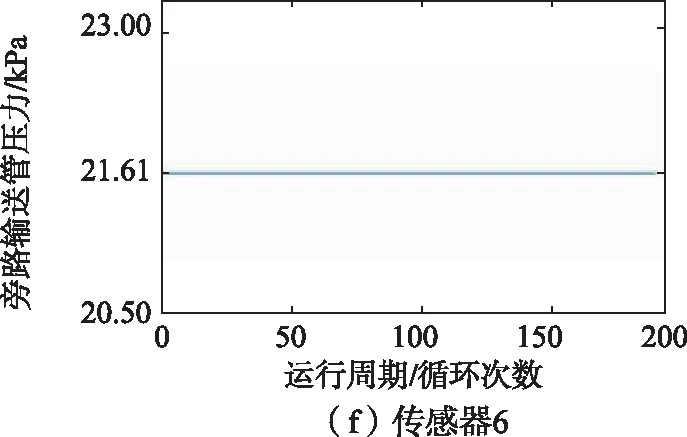
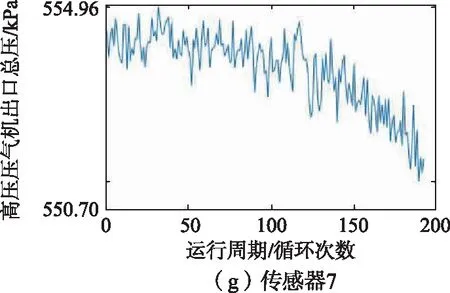
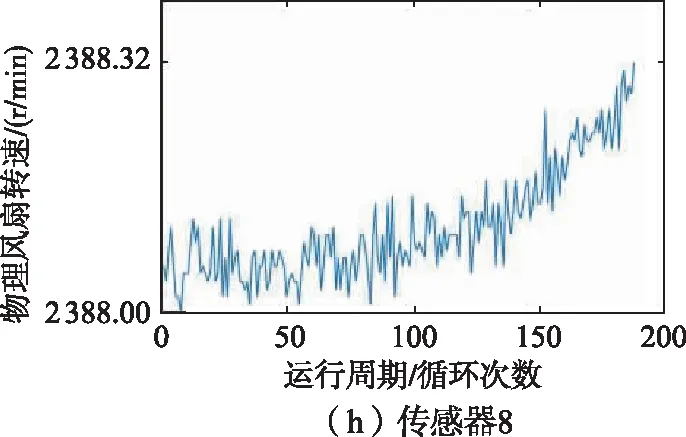
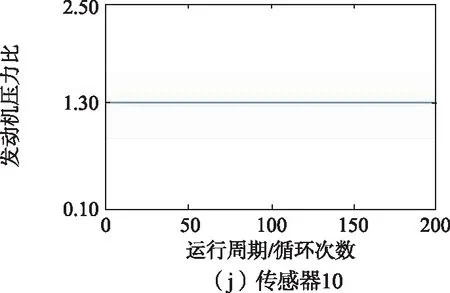
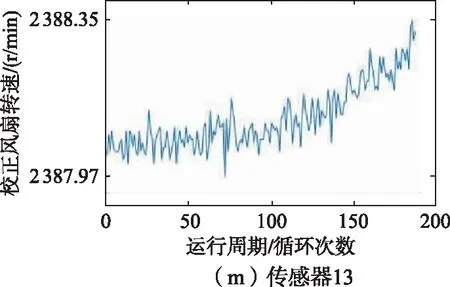
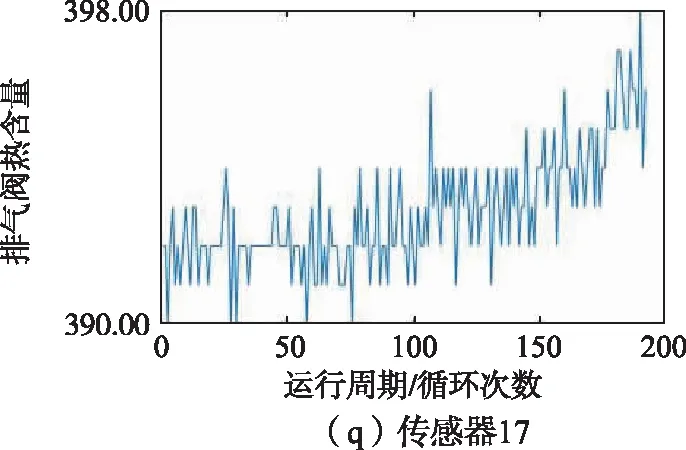
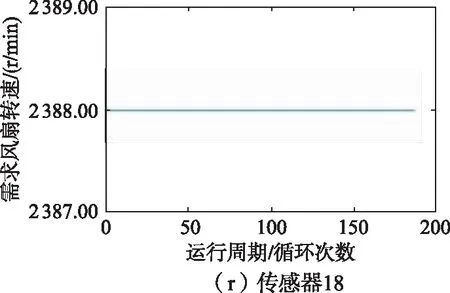
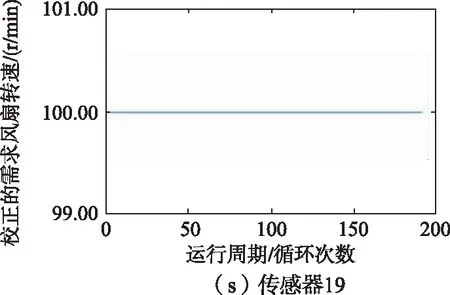
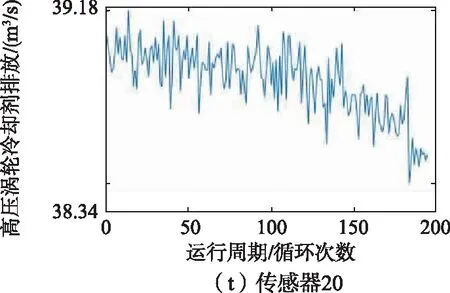
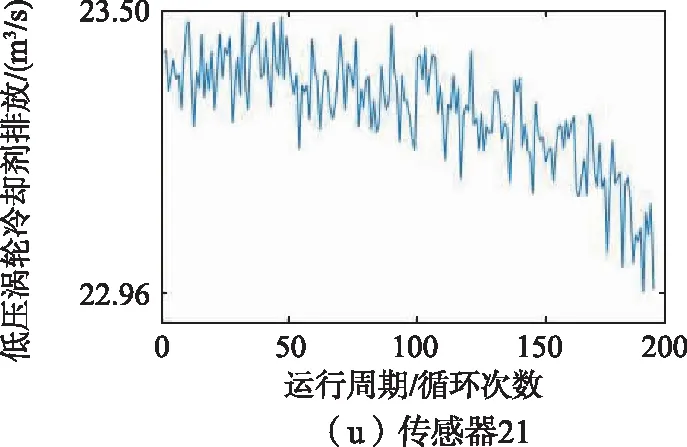
图6 1号发动机传感器监测数据变化趋势

利用Z-Score方法对特征参数进行标准化处理，计算式为：

(16)

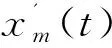
再利用分段线性函数给标准化后的特征参数贴上标签，分段点设置为130[23]。当发动机的剩余寿命大于等于130时，标签值为130，当剩余寿命小于130时，标签值依次递减1。

3.4 构造健康指标

根据1.1节中所提方法，求解得到训练集的融合系数为{W*}={0.300 4，0.205 5，0.792 3，-0.401 2，0.200 5，-0.148 5，0.794 3，-0.608 6，-0.024 5，0.223 1，0.519 1，0.485 0，-0.239 2，-0.414 5}，利用求解得到的融合系数，将处理好的训练集和测试集数据进行加权融合构造一维复合健康指标。训练集中1号发动机构造的一维复合健康指标如图7所示。

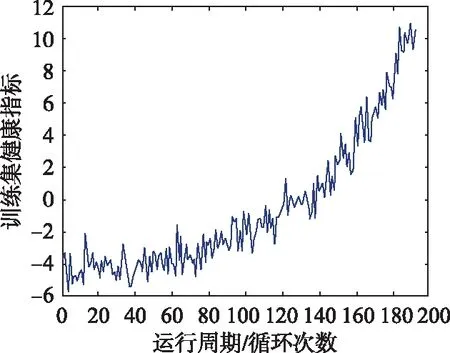
图7 1号发动机一维复合健康指标

本文选用Spearman相关系数来评估一维复合健康指标的优劣，对比了LSTM、t-SNE、1D-CNN和加权融合的方法(见表2)，结果证明利用加强融合方法构造的健康指标能更好地提取发动机的深层退化特征。

表2 健康指标对比

3.5 GRU预测模型的主要参数

参数见表3。

表3 GRU网络主要参数

3.6 实验结果及分析

图8给出的是模型预测误差(预测寿命-真实寿命)的分布情况，从图8中可以看出，预测误差在(-10，0]的发动机数量是最多的,超前预测的发动机数量和滞后预测的发动机数量近似相等。

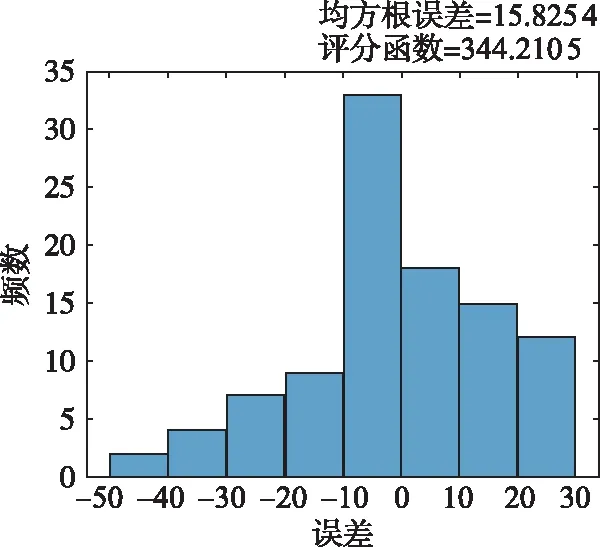
图8 误差分布直方图

图9中，随机展示了8号、49号、12号和100号测试集发动机剩余寿命的点估计和区间估计。从图9中可以看出，在发动机的整个退化过程中，不论是真实的退化过程还是模型预测的退化过程都在90%的置信区间。

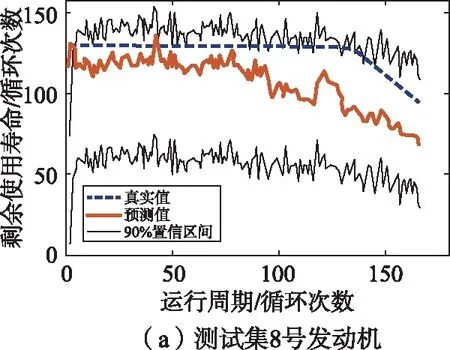
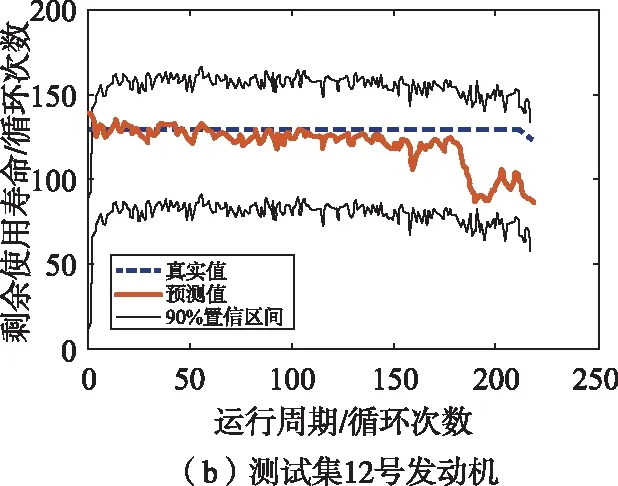
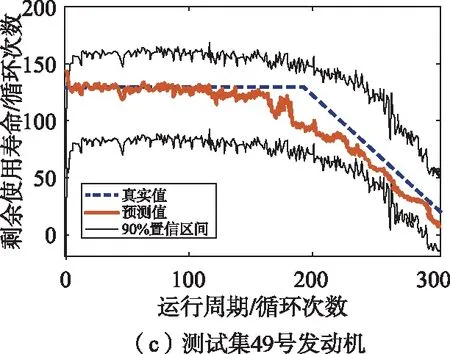
图9 测试集中的单个发动机剩余寿命预测结果

图10为100个测试集发动机的剩余寿命预测结果，为便于观察，按照图10中发动机真实剩余寿命的大小进行升序排序，可得如图11所示的预测结果。

图10 测试集发动机剩余寿命预测结果

从图11中，可以更加直观地看到，本文所提方法获得的预测结果与发动机的真实剩余使用寿命比较贴近，且测试集中100个发动机的真实剩余寿命和预测剩余寿命都在90%的置信区间。

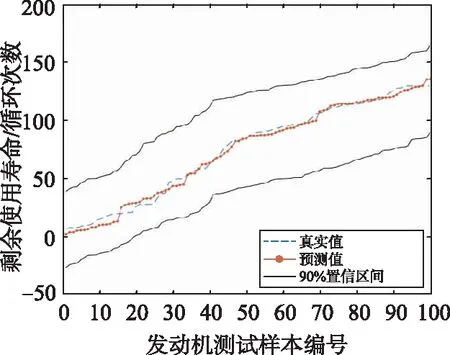
图11 测试集发动机剩余寿命预测结果排序

为了证明本文所提方法的性能，进行如下对比，结果见表4。

表4 对比结果

从表4中可以看出，与传统机器学习方法、单一深度学习网络、混合深度学习网络和其他深度学习与数理统计的组合方法对比，本文所提方法预测效果较好；与LSTM网络对比，两者预测效果近似，但GRU网络的运行时长缩短了124 s，有较高的运行效率。此外，若不使用加权融合的方法构造一维复合健康指标，而是选择直接将预处理好的14维传感器特征参数放入GRU模型中进行剩余寿命预测，这样做预测效果非但没有本文所提方法好，而且会因为数据维度多导致训练时长增加。