性能受限下的高超声速飞行器抗饱和控制

2023-01-07温林枝阴良魁

燕山大学学报 2022年6期

王芳，温林枝，阴良魁

(1.燕山大学理学院，河北秦皇岛 066004；2.中国科学院科技创新发展中心，北京 100190)

0 引言

高超声速飞行器是飞行速度超过5倍声速的有翼或无翼飞行器。随着科学与军事领域的发展，高超声速飞行器的跟踪控制研究已成为航空航天领域研究的热点问题之一。飞行环境复杂多变，导致高超声速飞行器具有强不确定性、强耦合性、强非线性和快时变等特性[1-2]。这些复杂特性导致高超声速飞行器控制的研究面临诸多难题。目前，基于高超声速飞行器纵向模型的控制方法主要有自适应反步控制[3]、滑模控制[4]和模糊控制[5]等方法，然而现有的控制方法仍然存在一些不足。因此，高超声速飞行器的控制研究是十分有意义的。

目前，针对高超声速飞行器受到的不确定问题，基于自适应技术的控制策略被提出[6-8]。文献[9]针对参数不确定，基于输入输出线性化理论，设计了模糊逻辑系统处理不确定问题。但这种方法处理不确定问题时一般需要比较复杂的计算过程，并且需要满足输入输出线性化的条件。此外，跟踪微分器也被用于处理高超声速飞行器的不确定问题[10]，然而这种跟踪微分器是二阶微分方程，且设计过程较复杂。上述方法虽然获得了良好的稳态跟踪性能，但没有考虑误差约束或状态约束等性能受限问题。事实上，实际系统对于性能约束有更高的要求。因此，设计性能受限下的控制策略可以确保系统满足预先设定的暂态性能和稳态性能要求。

目前实现暂态性能约束的主要控制方法有三类：预定性能函数(prescribed performance function,PPF)、障碍Lyapunov函数(barrier Lyapunov function,BLF)和状态变换函数。基于PPF的控制方法的主要思想是构造预定性能函数，将误差约束问题转化为无误差约束问题。文献[11]针对速度子系统设计了指数型性能函数。文献[12]针对不确定和未知干扰影响下的高超声速飞行器，设计性能函数和输出误差变换，确保输出误差满足预定性能要求。文献[13]采用误差变换函数解决了未知初始误差问题。此外，基于BLF的控制方法的主要思想是构造关于误差信号的BLF，然后根据BLF关于时间的导数设计控制器。文献[14]设计了BLF处理非线性系统的输出误差约束问题。对数型障碍Lyapunov函数[15-16]被广泛应用于解决非线性系统的性能约束问题。文献[17]利用对数障碍Lyapunov函数解决了高超声速飞行器的状态受限问题，并设计了基于固定时间干扰观测器的预定性能反步控制策略。文献[18]设计正切障碍Lyapunov函数(tangent barrier Lyapunov function,TBLF) 解决了非线性系统输出跟踪误差的性能约束问题。文献[19]提出了改进的TBLF，但输出误差约束的边界是对称的。文献[20]为了处理输出误差约束问题，提出了非对称TBLF，可以解决非对称的输出误差约束。状态变换函数方法的思想是构造与状态相关的非线性函数，将状态约束问题转化为状态无约束问题。无论是PPF方法还是BLF方法，改进方向都是设计新的函数，以确保约束效果更精确更灵活。因此，采用BLF方法实现对高超声速飞行器输出误差和所有状态误差的非对称约束是本文研究的重点之一。

此外，输入饱和是非线性系统的特性之一。如果输入饱和没有得到有效的处理，系统的控制性能会被迫减弱，甚至会产生系统不稳定现象[21]。由于高超声速飞行器的飞行环境复杂，未知气流会引发致动器饱和。所以在高超声速飞行器控制器设计中，输入饱和是不容忽视的问题。目前，通过在控制器设计的初始阶段考虑执行器幅值约束的方法可以用来解决执行器饱和问题[22-24]。然而，该方法保证了系统在执行器饱和影响下的稳定性，却牺牲了闭环系统的全局性能。辅助系统有效处理了输入饱和问题[25-26]。文献[27]利用高阶跟踪微分器，基于辅助误差构造了抗饱和自适应神经控制器，消除了执行器饱和的影响。但文献[27]在高度子系统中设计的辅助系统是三阶系统，这无疑会加大计算的复杂度。文献[28]在文献[27]的基础上，进一步改进辅助系统，所设计的辅助系统是有界的，且在有限时间内可以收敛到零。针对弹性吸气式高超声速飞行器的执行器饱和问题，文献[29]提出了抗饱和固定时间补偿器。此外，文献[30]结合双曲正切函数和辅助系统设计了抗饱和控制器，解决了高超声速飞行器输入饱和问题。文献[31]针对输入饱和问题，引入非线性增益函数提高了系统对输入饱和的抑制能力。文献[32]基于辅助系统设计了自适应容错控制器，解决了输入饱和问题。输入饱和以及性能约束是高超声速飞行器控制研究中不容忽视的两个问题。因此，针对不确定、性能约束和输入饱和综合影响下的高超声速飞行器控制器设计是本文的研究重点。

基于上述分析，本文的主要创新如下：

1) 基于非对称正切障碍Lyapunov函数，分别为速度子系统和高度子系统设计自适应障碍控制器和自适应障碍反步控制器，确保系统在不确定和输入饱和影响下，仍能使速度和高度跟踪误差以及状态误差满足约束的要求。

2) 采用辅助系统处理输入饱和问题，当发生饱和现象时，补偿器可以产生辅助变量，保证系统的稳定性，快速摆脱饱和区域。当不发生饱和时，辅助变量自动收敛，不会影响系统的控制性能，有效解决了输入饱和问题。

3) 结合非对称正切障碍Lyapunov函数和辅助系统设计自适应律，在性能约束和输入饱和情形下，有效解决系统中的不确定问题。

1 高超声速飞行器模型

本文基于高超声速飞行器纵向模型，进行跟踪控制的研究。相比于高超声速飞行器横侧向平面和六自由度轨迹跟踪控制研究，纵向动力学的特性更为丰富，研究方法也更具有代表性。高超声速飞行器纵向动力学模型为[33-35]

(1)

其中，V、h、γ、α、Q分别为速度、高度、航迹角、攻角和俯仰角速率，ηi为弹性变量(i=1,2,3)，Iyy、m、g分别为俯仰转动惯量、质量和重力加速度，T、D、L、Myy分别表示发动机推力、空气阻力、升力、俯仰力矩。力和力矩的近似值与文献[35]相同，由曲线拟合得到的气动力系数、力矩系数和广义力系数的表达式为

(2)

其中，

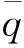
2 问题描述

本文的主要目的是为系统(1)设计控制器。首先为便于控制器设计，将纵向动力学模型式(1)改写为面向控制模型[36]，针对速度子系统和高度子系统分别设计辅助系统，解决输入饱和问题。其次，为解决误差约束问题，利用障碍Lyapunov函数确保输出误差和状态误差满足给定的性能要求。在高度子系统控制器设计中，利用滤波器避免了反步法存在的“计算爆炸”问题。

高超声速飞行器面向控制模型为

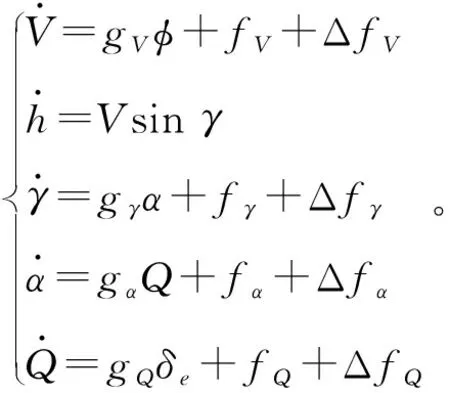
(3)

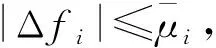
为满足预定性能对输出跟踪误差和状态误差的约束要求，本文利用非对称TBLF[20]

(4)

其中，ωi(t)=ωi0e-ζit+ωi∞，ωi0、ζi、ωi∞均为正常数，i=V,h,γ,α,Q。

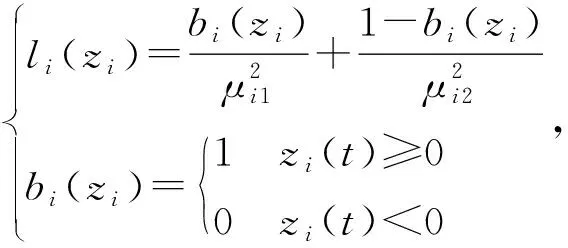
(5)

其中，μi1和μi2是正常数。

(6)

其中，ci1>0为待设计参数，

注1针对不确定问题，与文献[17]提出的非线性干扰观测器不同，本文在考虑预定性能和输入饱和的基础上，采用自适应方法对不确定的上界进行估计。所涉及的参数较少，计算更加简洁。

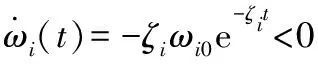
3 控制器设计

由面向控制模型式(3)可知，速度主要受燃料当量比的影响，而升降舵偏转对高度的贡献占主导地位。因此，式(3)可合理地分解为速度子系统和高度子系统。3.1节给出基于辅助系统的速度子系统抗饱和预定性能动态逆控制器设计过程；3.2节给出基于辅助系统的高度子系统抗饱和自适应反步控制器设计过程。

3.1 速度子系统控制器设计

在考虑控制输入φ饱和的情况下，通过设计带有辅助系统的控制器，有效补偿输入饱和。基于式(4)，针对速度子系统和辅助系统，设计关于速度跟踪误差的非对称TBLF，保证在飞行过程中速度跟踪误差不超过预设边界。

速度子系统动态方程为

(7)

考虑控制输入φ饱和

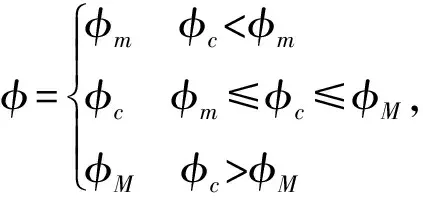
(8)

其中，φm、φM分别为φ的最小值和最大值。

为补偿控制输入饱和，设计辅助系统[25]

(9)

其中，Δφ=φ-φc，k0为正常数。

定义速度跟踪误差为

zV=V-Vd

(10)

其中，Vd为速度参考指令，对zV求导可得

(11)

设计如下Lyapunov函数

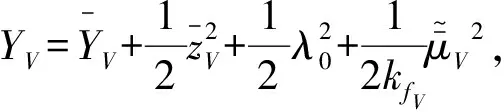
(12)

其中，kfV>0为常数。

由式(6)和式(11)可得YV关于时间的导数为

(13)

设计如下控制输入

(14)

其中，kV为正常数。

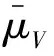
(15)

其中，kfV,σV>0为常数。

将式(14)和(15)代入式(13)，并利用杨氏不等式可得

(16)

注4与文献[21,25-26]相比，本文在考虑预定性能情况下处理输入饱和问题。对速度子系统和高度子系统分别设计辅助系统解决输入饱和问题。

3.2 高度子系统控制器设计

在考虑控制输入δe饱和的情况下，基于抗饱和辅助系统和非对称TBLF设计自适应反步控制器，保证在飞行过程中高度跟踪误差zh和状态误差zγ、zα、zQ不超过预设边界。

由于高超声速飞行器巡航段航迹角的变化较小，所以sinγ≈γ。高度子系统动态方程可以写为

(17)

其中，

考虑高度子系统控制输入δe饱和

(18)

其中，δem,δeM分别为δe的最小值和最大值。

为补偿控制输入饱和，设计辅助系统为

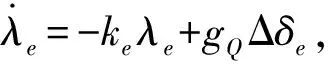
(19)

其中，Δδe=δe-δec,ke为正常数。

步骤1高度跟踪误差为

zh=h-hd

(20)

zh关于时间的导数为

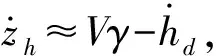
(21)

设计如下Lyapunov函数，保证高度跟踪误差始终保持在预定范围之内

(22)

根据式(6)和式(21)，对Yh求导可得

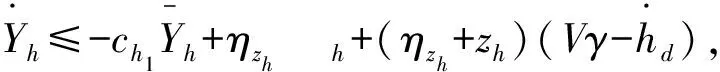
(23)

设计虚拟控制输入γc

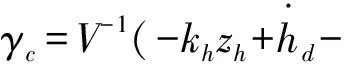
(24)

其中，kh为正常数。将式(24)代入式(23)得

(25)

为避免虚拟控制输入多次求导产生“计算爆炸”问题，设计一阶滤波器

(26)

其中，τγ为正常数，滤波器误差为yγ=γd-γc。

步骤2航迹角误差为

zγ=γ-γd，

(27)

zγ关于时间的导数为

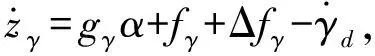
(28)

设计如下Lyapunov函数，保证航迹角误差始终保持在预定范围之内

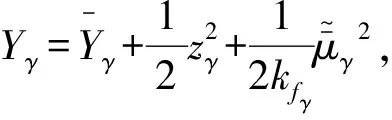
(29)

其中，kfγ为正常数。

由式(6)和式(28)可得Yγ关于时间的导数为

(30)

设计虚拟控制输入

(31)

其中，kγ为正常数。

设计如下自适应律

(32)

其中，σγ>0是正常数。

将式(31)和(32)代入式(30)，并利用杨氏不等式得

(33)

设计如下一阶滤波器

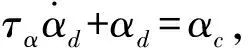
(34)

其中，τα为正常数，滤波器误差为yα=αd-αc。

步骤3攻角误差为

zα=α-αd

(35)

zα关于时间的导数为

(36)

设计如下Lyapunov函数，保证攻角误差始终保持在预定范围之内

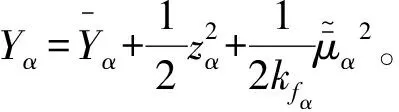
(37)

由式(6)和式(36)可得Yα关于时间的导数为

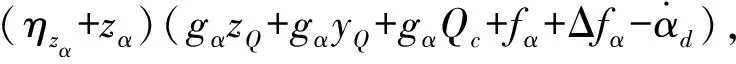
(38)

设计虚拟控制输入

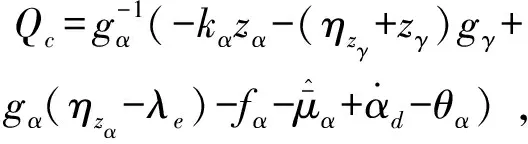
(39)

其中，kα为正常数。

设计如下自适应律

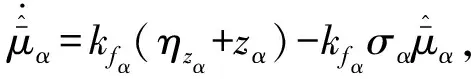
(40)

其中，σα>0是正常数。

将式(39)和(40)代入式(38)，利用杨氏不等式得

(41)

设计如下一阶滤波器

(42)

其中，τQ为正常数，滤波器误差为yQ=Qd-Qc。

步骤4俯仰角速率误差为

zQ=Q-Qd

(43)

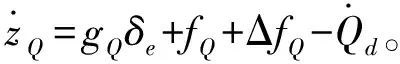
(44)

设计如下Lyapunov函数，保证俯仰角速率误差始终保持在预定范围之内

(45)

由式(6)和式(44)可得YQ关于时间的导数为

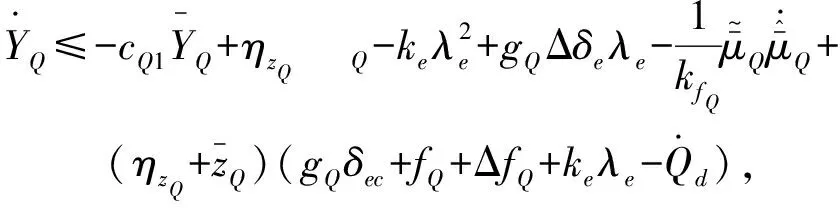
(46)

设计控制输入

(47)

其中，kQ为正常数。

(48)

其中，σQ>0是正常数。

将式(47)和(48)代入式(46)，并利用杨氏不等式得

(49)

4 稳定性分析

基于上述控制器的设计，通过Lyapunov稳定性理论分析其稳定性。

定理1考虑系统(1)，在假设1和假设2成立的条件下，设计控制输入式(14)和式(47)以及自适应律式(15)和式(48)。则系统输出跟踪误差zV,zh和状态误差zγ,zα,zQ满足预先设定的约束条件。

证明选取Lyapunov函数为

Y=YV+Yh+Yγ+Yα+YQ+Yy

(50)

由一阶滤波器(26)、(34)和(42)可得

(51)

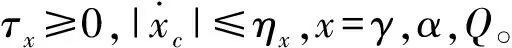
基于式(16)、(25)、(33)、(41)、(49)和(51)，式(50)关于时间的导数为

(52)

进一步可得

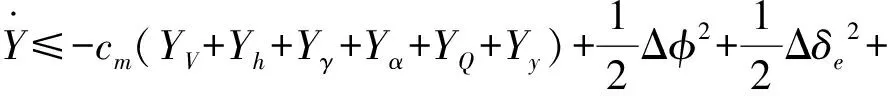
(53)

由(53)可得

Y≤Y(0)e-cmt+c0/cm

(54)

进一步可得输出速度跟踪误差zV、高度跟踪误差zh以及各状态误差zγ,zα,zQ有界

由式(4)和(5)可知

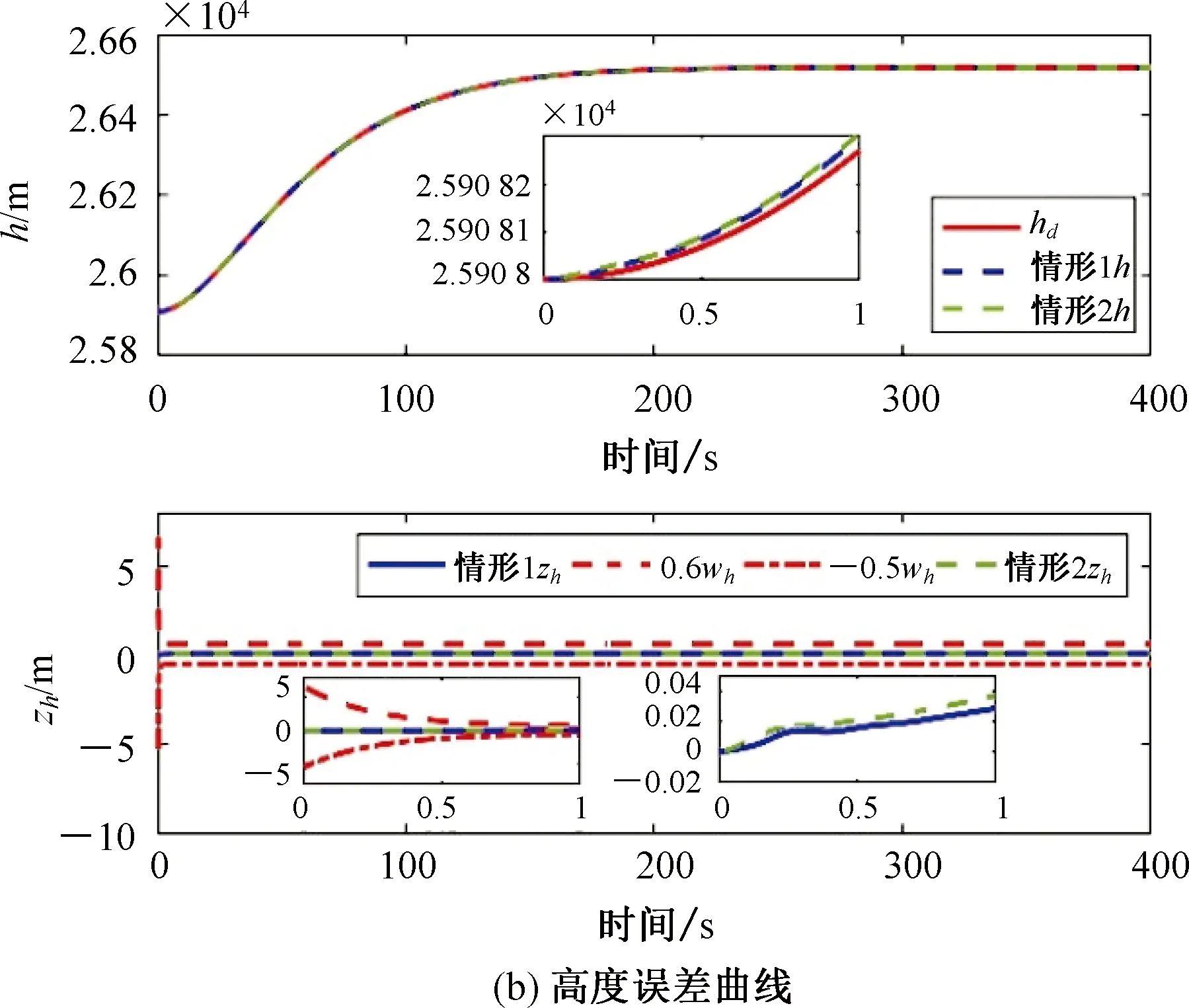
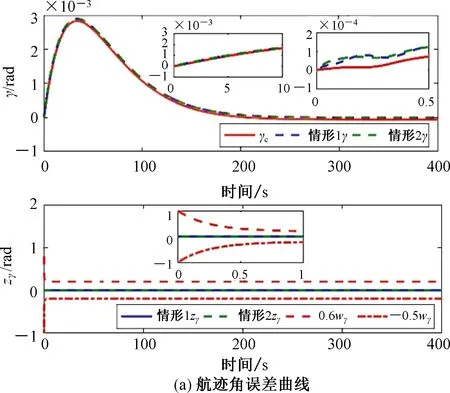
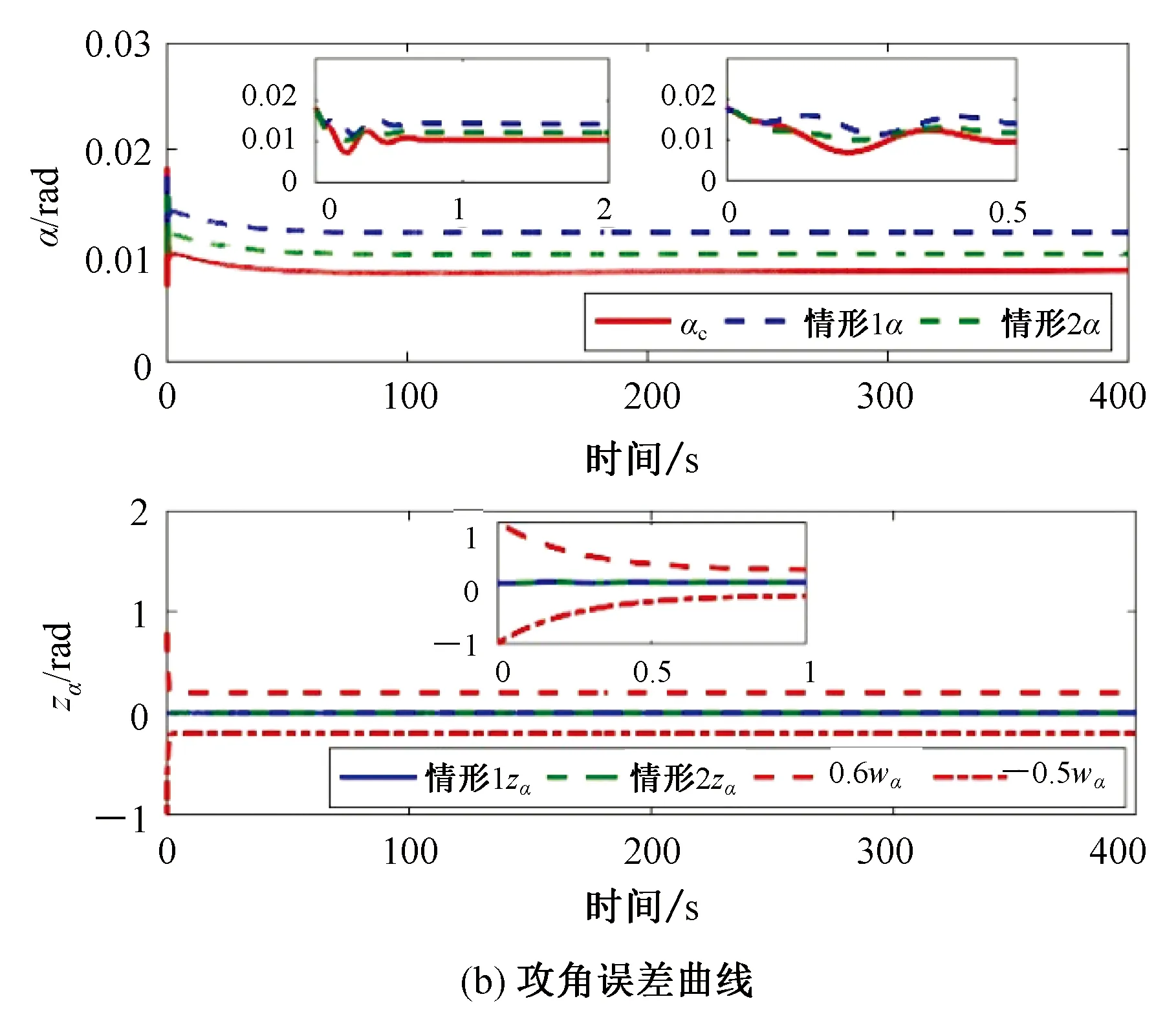
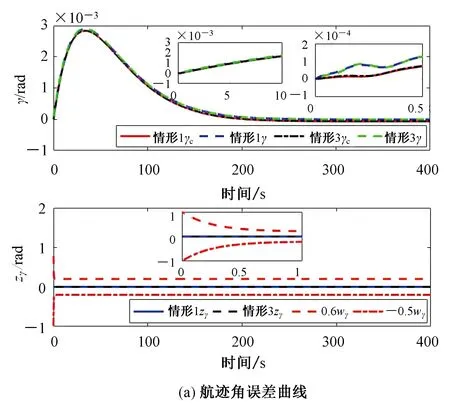
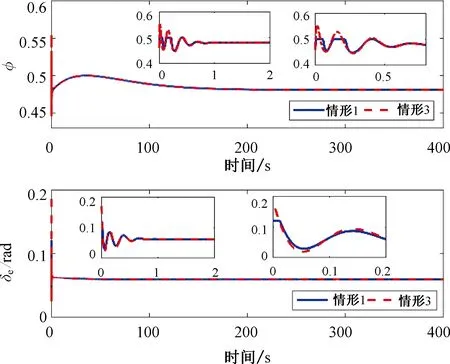
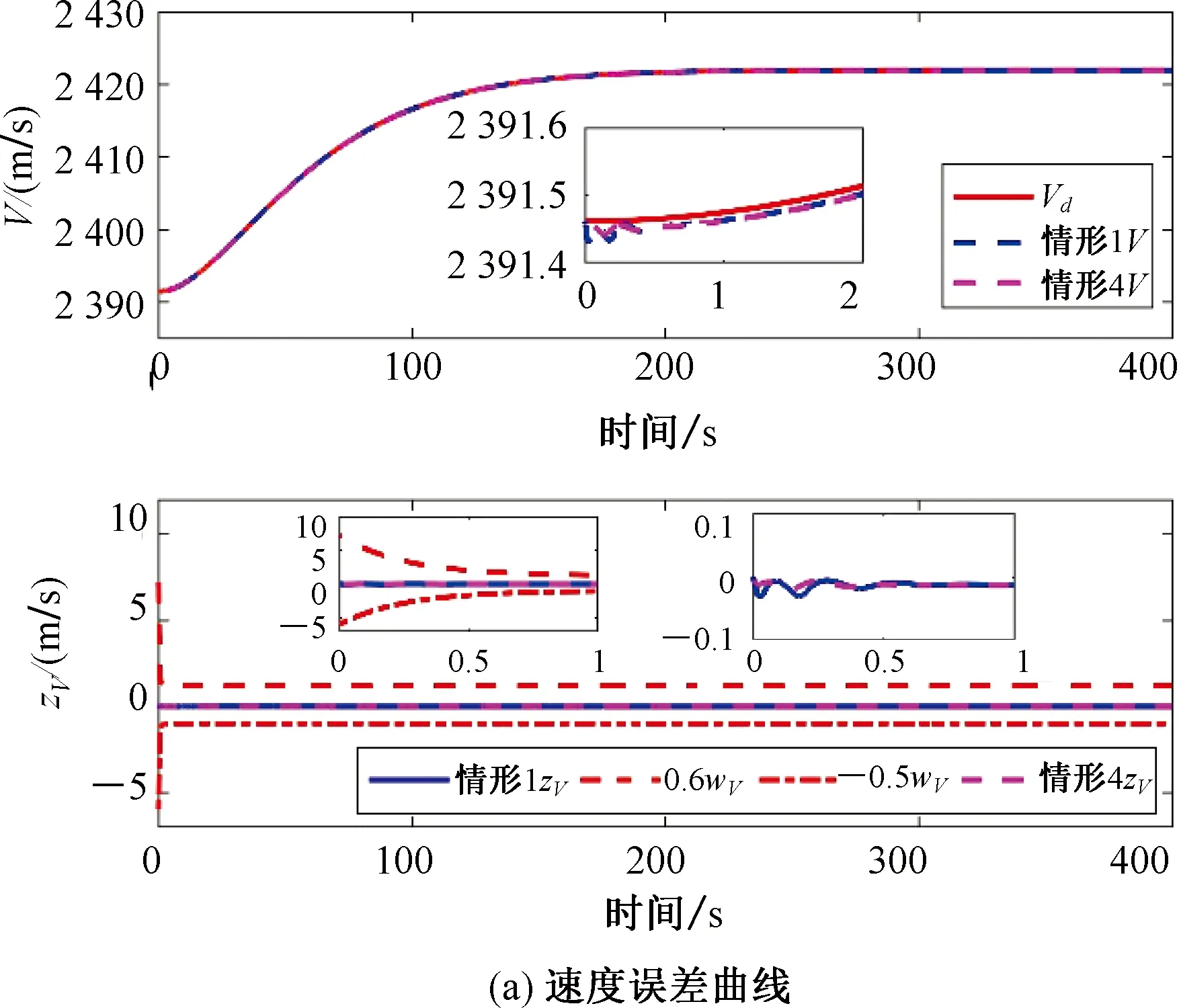
因此，所提控制策略能够保证系统跟踪误差及各状态误差是有界稳定的，且满足预先设定的性能要求-μi2ωi(t)

5 仿真分析

为了验证速度子系统和高度子系统自适应控制器的有效性，以高超声速飞行器的非线性纵向动力学模型(1)为仿真对象。仿真时参数的不确定性为+20%。飞行器速度和高度的阶跃信号分别为30.48 m/s和609.6 m。飞行器初始条件如表1所示。所设计控制器的参数如表2所示。控制输入饱和的最大最小值分别为φm=0.1,φM=0.5和δem=-0.12 rad,δeM=0.12 rad。

表1 状态初始值Tab.1 Initial flight condition

表2 控制器参数Tab.2 Controller parameters

为验证所提出的控制策略的有效性，针对如下四种情形进行对比仿真：

情形1考虑不确定、输入饱和与预定性能。

情形2只考虑输入饱和与预定性能。

情形3考虑不确定与预定性能。

情形4考虑不确定、输入饱和与预定性能。

利用如下对数型障碍Lyapunov函数[17]保证系统满足预定性能要求：

其中，ρV(t)=(ωi0-ωi∞)e-lVt+ωi∞,i=V,h,γ,α,Q,ωV0=7,ζV=4,ωV∞=1,ωh0=6,ζh=4,ωh∞=0.6,其余参数同表2。

图1～图3为情形1与情形2下的对比结果。通过图1(a)和(b)可以看出，两种情形下，速度曲线V和高度曲线h都能稳定跟踪其期望轨迹Vd和hd，并且速度跟踪误差zV和高度跟踪误差zh都在预先设定的范围内(-0.5ωV,0.6ωV),(-0.5ωh,0.6ωh)。由图2(a)～(c)可知两种情形下，航迹角γ、攻角α和俯仰角速率Q实现了对各自期望信号的稳定跟踪，且误差在预先设定的范围内(-0.5ωγ,0.6ωγ),(-0.5ωα,0.6ωα),(-0.5ωQ,0.6ωQ)。图3为控制输入φ和δe在情形1和情形2下的对比曲线。在所设计的预定性能控制策略下，燃油定量比φ和升降舵偏角δe均趋于稳定。

图1 情形1与情形2的输出误差曲线Fig.1 Error curve of output in case 1 and case 2

图2 情形1与情形2的状态误差曲线Fig.2 Error curve of states in case 1 and case 2

图3 情形1与情形2的控制输入曲线Fig.3 Curve of control input in case 1 and case 2

图4～图5为情形1与情形3的对比结果。通过图4可以看出，在两种情形下，速度V和高度h都能稳定跟踪其期望轨迹Vd和hd，并且速度跟踪误差zV和高度跟踪误差zh都在预先设定的范围内(-0.5ωV,0.6ωV),(-0.5ωh,0.6ωh)。由图5可知，在两种情形下，航迹角γ、攻角α和俯仰角速率Q实现了对各自期望信号的稳定跟踪，且误差在预先设定的范围内(-0.5ωγ,0.6ωγ),(-0.5ωα,0.6ωα),(-0.5ωQ,0.6ωQ)。

图4 情形1与情形3的输出误差曲线Fig.4 Error curve of output in case 1 and case 3

图5 情形1与情形3的状态误差曲线Fig.5 Error curve of states in case 1 and case 3

图6为控制输入φ和δe在情形1与情形3的对比曲线。在情形3下，燃油定量比φ和升降舵偏角δe分别在(0,0.2)s和(0,0.1)s内出现饱和现象。分别超出约束φ∈[0.2,0.5]和δe∈[-0.12,0.12]rad，并在0.7 s后趋于稳定。通过对比可以得出所设计的控制策略可以有效补偿控制输入饱和，并且比不考虑饱和的情形使系统具有更良好的稳定性。

图6 情形1与情形3的控制输入曲线Fig.6 Curve of control input in case 1 and case 3

图7为情形1与情形4的速度跟踪误差曲线和高度跟踪误差曲线。通过图7可知，在两种情形下，速度跟踪误差zV都在约束边界内且区别较小。此外，利用非对称TBLF时的高度跟踪误差zh在(0,2)s内小于利用对数型障碍Lyapunov函数时的高度跟踪误差。这表明非对称TBLF比一般的对数型障碍Lyapunov函数具有更强的约束性。并且非对称TBLF对误差的约束边界既可以是对称的又可以不对称的，这优于只能保证对称约束边界的对数型障碍Lyapunov函数。