基于超声解调信号多特征融合的轴承故障识别

姜浪朗，张敬超，江国乾，苏连成，李英伟,*

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

0 引言

轴承常用于旋转机械设备中，因为受各种恶劣坏境和长时间运转的影响，所以轴承也是旋转机械中最容易损坏的一个零部件。根据统计，超过1/3的机器损坏或失效都是由轴承引起的。轴承的运行状态对设备的生命周期、现场操作工人的安全等都有重要的影响[1]。因此，对工作中的轴承进行实时状态监测，发现早期故障而采取相应的针对性维护措施，对延长设备使用、保证工作环境安全和增加企业经济效益，均有现实意义和实际价值[2]。

当前，为获取轴承的状态信息，针对振动信号的特征提取和状态判断等处理措施[3]，国内外已经展开了大量的研究工作，并在电力、车辆、化工等行业取得较好的效果。在振动监测中，文献[4]系统说明了轴承故障类型和故障特点，且描述了故障预警与判断的方式，文献[5]引用振动信号卷积神经网络法来将数据分类，文献[6]以小波包变换处理振动信号，文献[7]以傅里叶变换和小波包变换相组合来识别轴承的状态信息，证明其结合后增强状态识别的精准度。但对于低速运转的设备，故障产生的信号频率较低，大多时候低频信号都会被过滤掉，导致部分故障信号被埋没，故对振动信号进行分析时效果不太精准，且在振动信号中获取故障早期特征较为困难。

实际上，轴承从轻微磨损到最后严重的损坏变形有具体的失效过程[8-9]。因为当轴承产生欠润滑、微磨破损等状态时，通常会自发产生一种高频信号。这种信号有别于低频振动(通常频率是20 Hz～20 kHz，此类范围人耳可以听到)，而高频信号为高频短波信号，其频率范围为20 kHz～100 kHz，它可有效避免工业现场大量低频噪声信号等的干扰(包括大部分环境噪声)，从而能够提供更敏感有效的状态信息，但20 kHz～100 kHz的高频信号数据量极大，对后期的采集、存储和信号处理都极为不便，故本次处理的信号为高频信号经过降频之后的超声解调信号，其频率范围在20 kHz以下。相较于振动信号，经过超声解调之后的信号具有更高的信噪比，对设备的润滑状态或早期磨损极为敏感，故超声解调信号更适用于传动设备的状态监测。

特征提取过程对于轴承状态的识别至关重要，且仅用一种或者一类的特征来判断会使结果受限，故本文提出一种基于经验模态分解与多类熵值相结合的轴承状态监测方法，此方法使用经验模态分解后的各分量与多类熵值结合来进行特征提取，并使用随机森林算法构建分类模型进行状态诊断，结果表明，相较于单一特征，多特征融合方法对轴承早期故障有更好的区分效果。

1 特征提取与状态诊断方法

1.1 EMD分解原理

经验模态分解(Empirical Mode Decomposition, EMD)，可将复杂的信号根据频率从高到低依次分解为若干本征模态函数(Intrinsic Mode Function, IMF)，可用来处理非周期性、非线性的信号[10]。此方法有两个约束条件：1)过零点数目以及局部的零值点在全部时间轴范围内要保持一致或仅差一个；2)在任何时间范围点内其上下包络线均值要等于0。EMD分解流程图如图1所示。

图1 EMD分解流程图Fig.1 EMD decomposition flow chart

1.2 随机森林算法

随机森林算法是Leo Breiman在2001年时提出的一种方法[11]，主要是对样本使用多棵决策树来训练并且预测的一种集成分类器，它的原理就是利用随机生成的决策树来给出最终的判断结果。随机森林的优点是：相较单棵决策树而言，随机森林可以使用多棵决策树来进行判断，所以并不依赖于一个决策树来判断最优特征，可使其每棵树的创建都有自己独立的样本集；因为单一的算法有其局限性，而它采用的集成算法可以使判断准确率大大提升；较快的训练速度可以使这种方法在处理大量数据集时效果更佳。

随机森林算法的主要处理过程如下：

1)从样本集中有放回的随机采样选出n个样本；

2)从所有特征中随机选择k种较为重要的特征，然后以这些特征为样本建立决策树；

3)重复以上两步m次，即生成m棵决策树，形成随机森林；

4)经过每棵树的决策及判断后，最终得出影响因子最大的前几名特征值用于状态判断。

1.3 多特征融合识别算法

本文提出了一种EMD分解与多类熵值结合的特征提取方法，实现超声解调信号的多尺度分解和故障特征的分频带划分，通过计算EMD分解后不同分量的多类能量熵，实现能量分布的量化描述，来提取到更优的特征值。再通过随机森林进行模型训练，利用混淆矩阵进行最终的准确率评估。具体步骤如下：

1) 通过实验轴承获取不同运行状态的超声解调信号。

2) 将各类不同轴承状态的原始信号使用七点三次平滑法进行预处理，使其得到更加平稳的信号便于下一步更好的特征效果提取，再将平滑后的数据进行均等化分帧的操作，将每种数据的类型分成5 512点为一帧，一类状态数据共有40 s，采样率为22 050 Hz，即一类状态数据共分160帧。

3) 通过EMD自适应分解来获取轴承不同状态超声解调信号各种尺度的IMF分量，一种状态会被分成12组左右的IMF分量，考虑后面几组能量值太小，因此将其舍去，选取能量值信息较高的前7层应用于下一步计算。

4) 对提取分解后的不同层IMF分量值计算样本熵[12-13]、排列熵[14]、小波熵[15]、近似熵[16]等多类熵值。

5) 将EMD提取后的前7层本征模态分量与多类熵值进行结合，通过优化后的特征向量用于随机森林构建分类模型，进行参数调优提升模型精确度，再利用混淆矩阵[17]进行精度评价，并进行特征择优获取影响因素较好的特征值。

多特征融合算法整体流程如图2所示。

图2 多特征融合算法整体流程Fig.2 Overall flow of multi-feature fusion algorithm

2 实验数据分析

2.1 实验数据的获取

本实验数据是在实验室的轴承上采集得到的，本次采集平台所使用的轴承转速为1 050 r/min，分别在轴承内部添加不同大小的磨粒，使其模拟出轴承的三类不同运行状态：正常状态、轻微磨损状态、严重损坏状态。在数据采集时，采样参数为采样率22 050 Hz、单通道、16位采样，单次采样时间持续10 s。再对不同状态的各4组数据进行组合分析，在基础分析时，提取每类样本单次点数为5 512。实验轴承数据采集流程如图3所示。

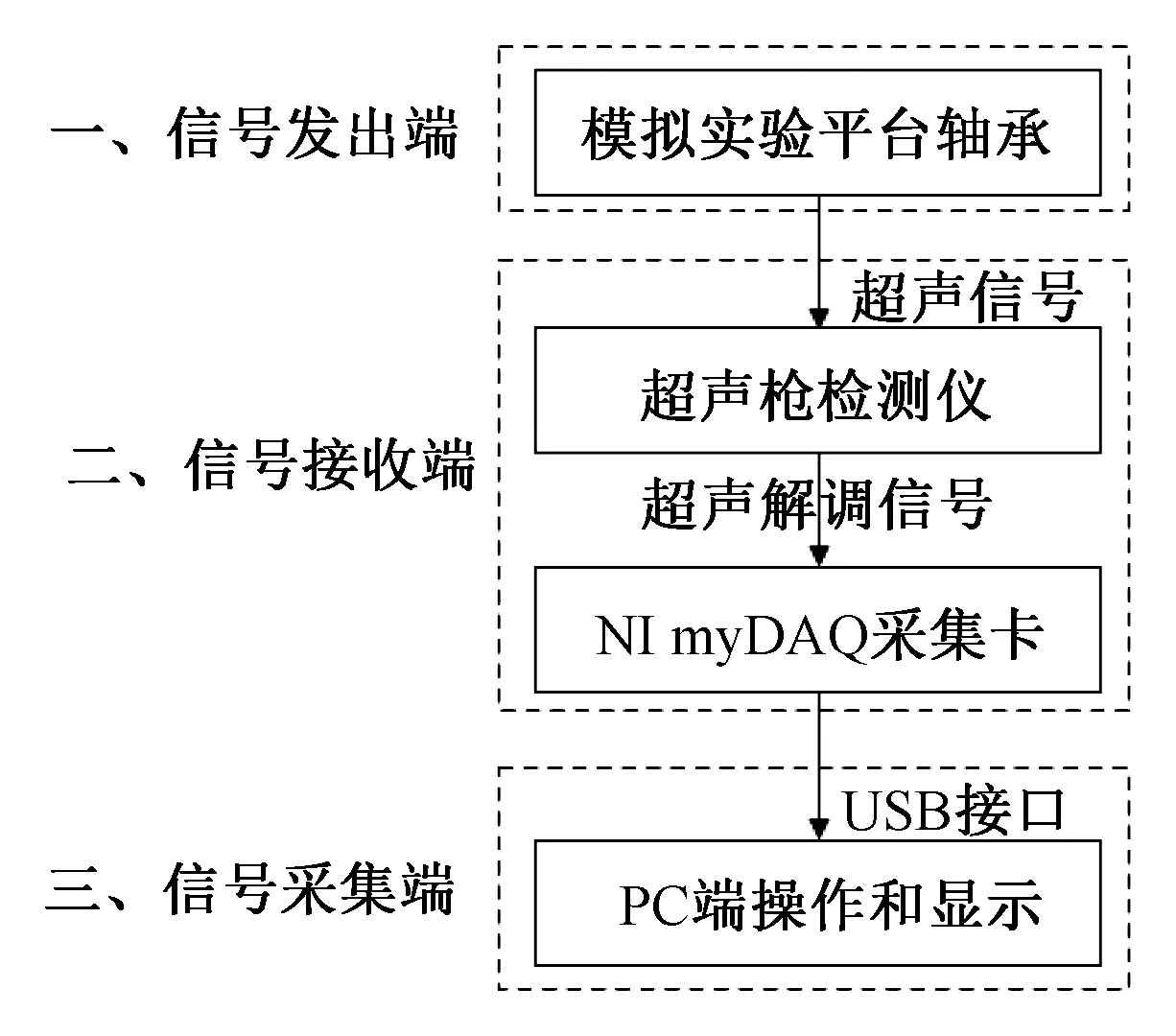
图3 实验轴承数据采集流程Fig.3 Experimental bearing data collection process

2.2 实验数据平滑预处理

在实验轴承上采集到的轴承超声解调数据往往会受到噪声的轻微干扰。常见的噪声信息有周期性的也有非周期性的，50 Hz工频干扰是周期性的常见来源，随机信号是非周期性噪声的重要因素。

为消除上述两类噪声干扰对数据分析带来的影响，以及提取数据更稳定的特征值，需要先对数据进行平滑预处理。常见的平滑处理算法有：样条插值函数平滑法、平均值计算平滑法以及五点三次平滑法[18]等。在这些方法中，样条插值函数方法虽较为灵活且有一定效果，但其计算方式繁琐，且对幅度平滑效果较差；平均值计算方法的滤波效果并不理想；五点三次方法有较好滤波效果，对幅度平滑效果较好，但需要多次计算。本文基于五点三次平滑算法改进成七点三次平滑算法，其有较为快速的计算方式，较好的滤波效果，且能保存较为稳定的数据信息。

t-s=-s,t-s+1=-s+1,…,t-1=-1,t0=0,
t1=1,…,tn-1=n-1,tn=n,

此时将得到的实验数据用m次多项式进行拟合，则拟合多项方程式为

Y(t)=a0+a1t+a2t2+…+amtm

(1)

接着，用最小二乘法推导(1)里的待定系数，令

(2)

为使φ(a0,a1,…,am)达到最小，让式(2)分别对ak(k=0,1,…,m)求导，令求导结果为零，可得

(3)

式(3)称为正规方程组。当n值为3(即7节点)，m值为3后，可计算出其正规方程组，可解出a0,a1,ai,ait，代入式(3)，令t值分别为0,1,-1,2,-2,3,-3,则可以解出a0,a1,a2,a3值为

(4)

(5)

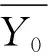
将轴承信号数据集经七点三次平滑算法进行去噪预处理，数据去噪效果对比如图4所示。由图4可以很明显地看出去噪的效果，因此本方法在数据预处理时是可行的。

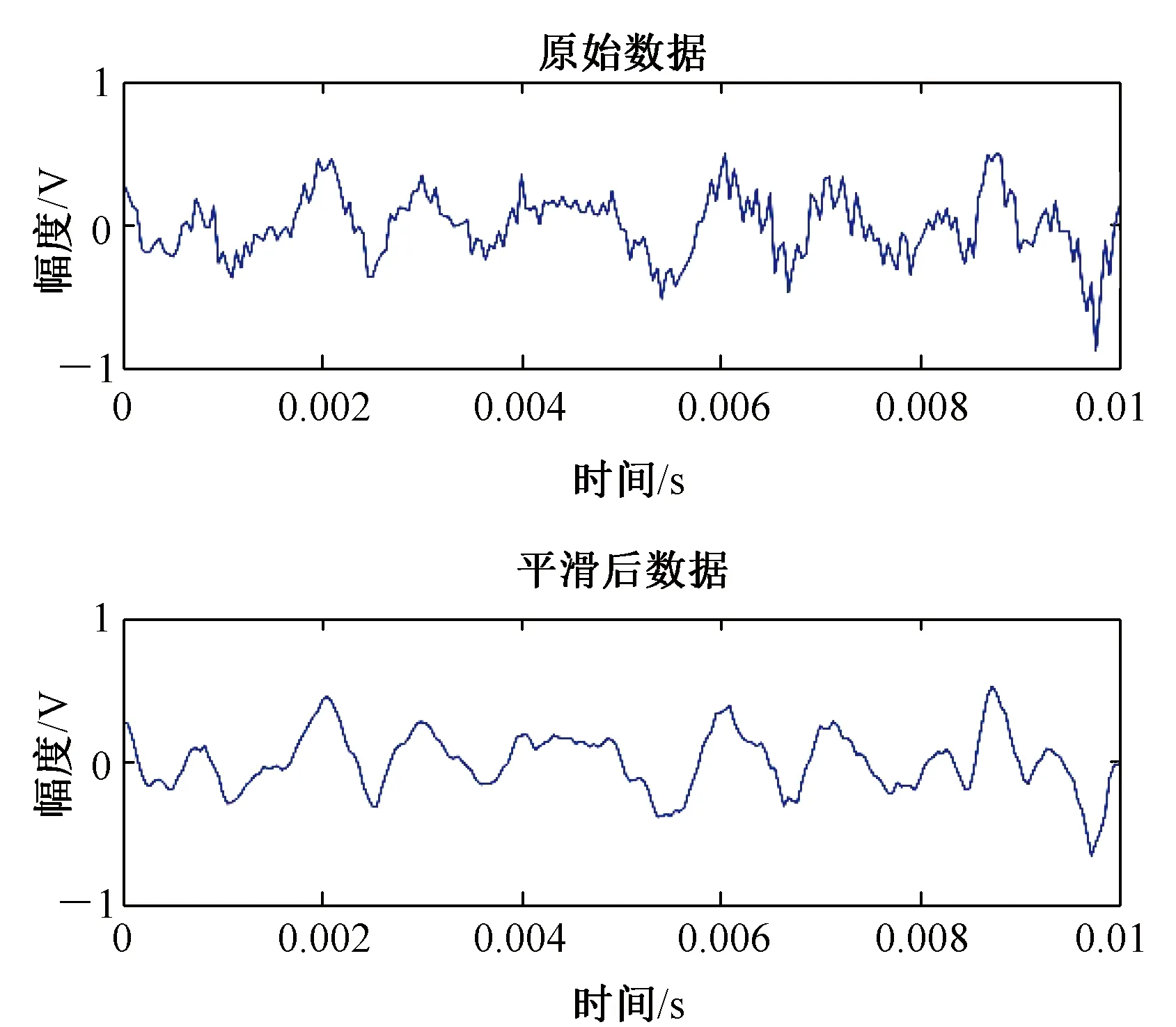
图4 数据去噪效果对比Fig.4 Comparison of data denoising effect

2.3 数据的时频域基础分析

首先，对预处理后的信号进行初步时频域分析对比，轴承三种状态的时频域信号如图5所示。

图5 轴承三种状态的时频域信号Fig.5 Time-frequency domain signals of bearing in three states

从图5可得出，轴承不同状态的超声解调信号幅值有所不同，正常时呈现近周期稳定波动；微损时有间断性波动，其幅值在0.5 V左右，当严重时呈现极大不规律性，最大值近1 V左右。正常状态和微损状态的频谱较为相似，但微损轴承会在0.5 kHz左右时产生较大的波动，三种状态均在0～3 kHz内出现主频成分，而严重故障状态的频谱频带较宽，且呈现一定的分布特性。故在实践中可通过信号幅值和频域初步判断轴承状态。

2.4 多类熵值融合的特征提取

根据2.3节的分析，可以从时域中看出微损轴承比正常轴承的幅值大且局部有较大波动，但是间歇性出现的波动也极可能是现场各类不确定噪声或采集数据时人为误差造成的，并且微损幅度出现的波动和频率存在不稳定的非周期性，故仅从时频域分析数据存在一定局限性，无法准确区分轴承运行时不同的状态类型，尤其是早期故障的产生，单纯靠人的经验值来判断是不科学的，这样容易发生误判或漏诊。因此，需要更深一步对信号进行EMD分解，实现超声解调信号的多尺度分解和故障特征的分频带划分，通过计算不同分量的多类能量熵值来深入判断。超声解调信号经过EMD分解后，提取前7层IMF分量值，不同频率分量蕴含轴承各类状态信息，三种状态轴承前7层分解信号图如图6所示。

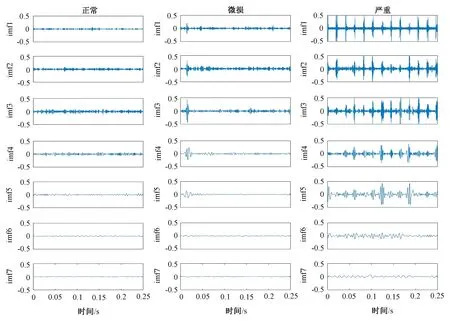
图6 三种状态下轴承前7层分解信号图Fig.6 Decomposition signal diagram of the first 7 layers of the bearing in the three states

由图6可以得出，三种不同状态的轴承通过EMD分解，从高频至低频自适应分解成不同的分量值，每层分量都蕴含着不同的特征信息，实现了轴承状态多频带的划分，因此可以通过每一层频率段提取更为精准的分类特征。

接下来，为进一步明确和细化不同轴承状态，采用EMD分解后提取各层的IMF分量来计算不同种类熵值，得到各类状态信号的不同特征，从而反映故障信号的非周期性特征并绘制折线图。同时，在进行分析时，考虑到相比较单组数据的局部波动性，本次实验每种状态选取10 s的数据，每种状态分成40段，每段5 512个点，将每段数据都进行EMD分解后，舍弃后面的分量较小的层数以及误差层，本次主要分析取前7层，提取出每一层的40段数据并计算其平均值，构建成新的7层IMF分量后计算其不同熵的能量值，计算后的7层分解样本熵、排列熵、小波熵、近似熵状态如图7～10所示。

图7 7层分解样本熵状态Fig.7 Sample entropy state of 7-layer decomposition

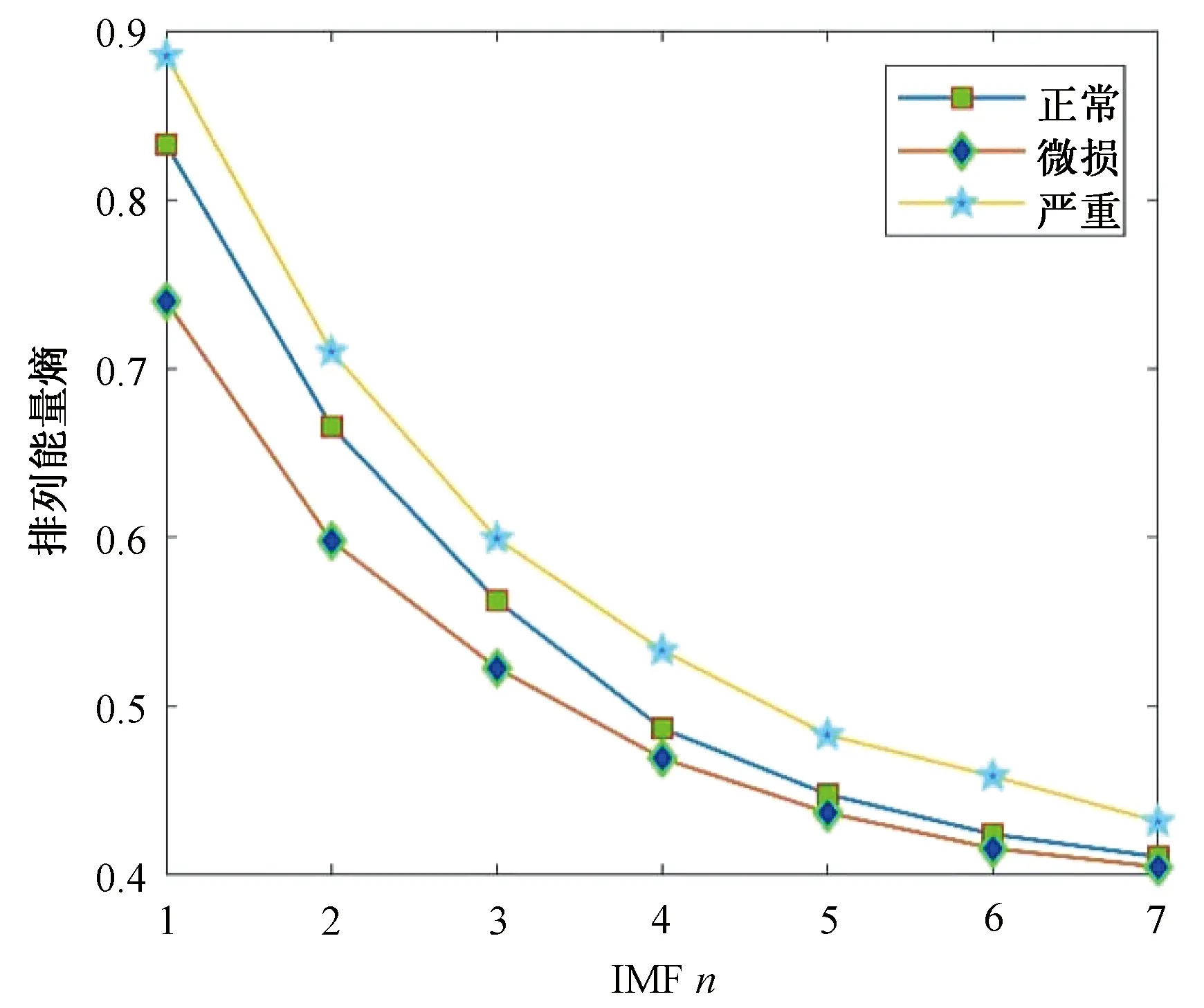
图8 7层分解排列熵状态Fig.8 Permutation entropy state of 7-layer decomposition

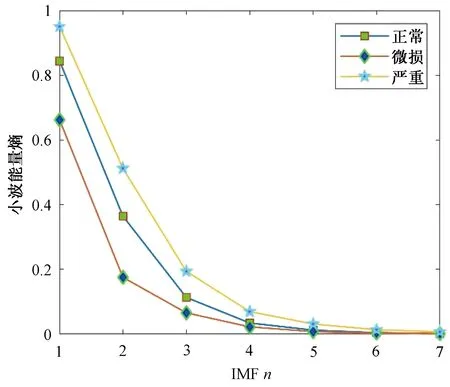
图9 7层分解小波熵状态Fig.9 Wavelet entropy state of 7-layer decomposition

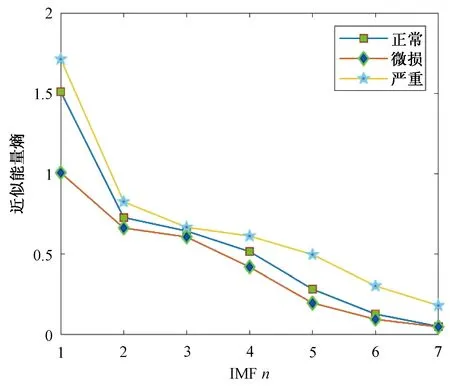
图10 7层分解近似熵状态Fig.10 Approximate entropy state of 7-layer decomposition

实验结果表明，经EMD分解后的不同熵值能量随着分解层数的增加都呈现降低趋势，对于不同状态的同一熵值的情况，在逐层分解时，严重故障状态较正常状态的熵值普遍较高，而微损状态较正常状态的熵值普遍较低，这就为判断早期故障提供了良好的保障。而且多类熵值的计算方式也较为简单，为后期的在线监测系统打下良好基础。

2.5 多特征融合的轴承故障识别

本次实验针对EMD分解后的1～7层分量与样本熵、排列熵、小波熵、近似熵进行结合，得到28维特征值，将其代入多特征随机森林构建分类模型。对选取的样本随机抽取等比例值进行训练，通过对随机森林参数不断择优，找到最佳参数的随机森林模型后，对测试集进行准确率判别，利用混淆矩阵进行精度评价，并对28维特征值进行择优，得出对状态评价影响较高的特征值。在模型训练时，令正常轴承状态标签为1，微损轴承状态标签为2，严重轴承状态标签为3，每种状态训练样本为112个，测试样本为48个。最终轴承状态识别准确率见表1。

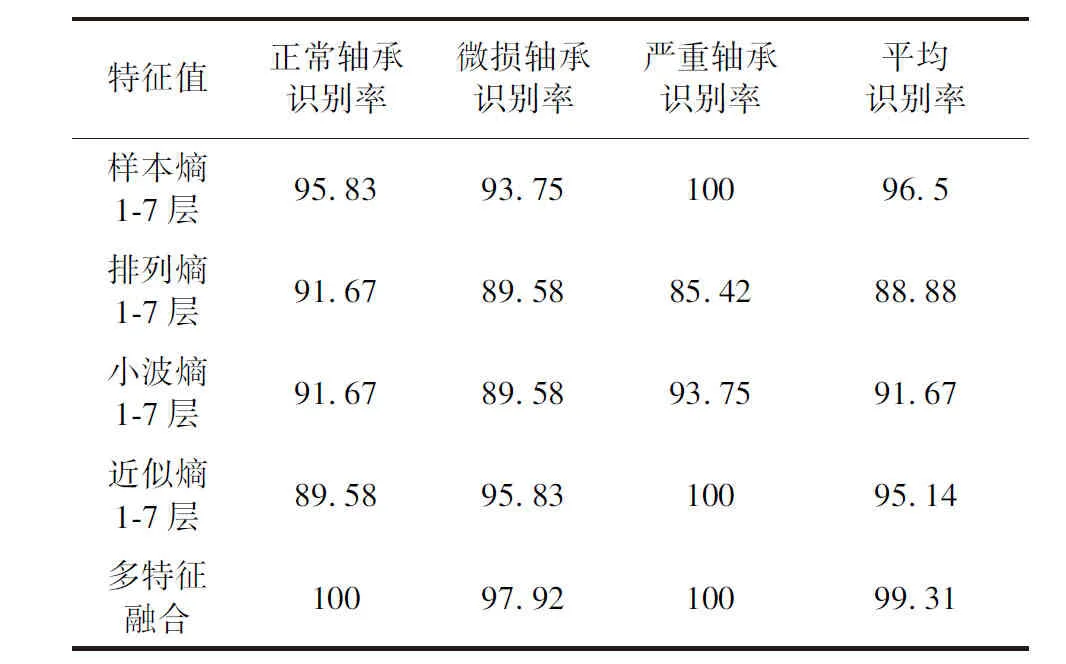
表1 轴承状态的识别准确率Tab.1 Accuracy of identification of bearing status %

数据分析时，考虑单次轴承状态数据的偶然性，本次针对不同时间段4次采集到的三种状态各10 s数据(即每种状态共40 s数据)进行分析，将其分成160组(每组5 512个点)进行EMD分解和多类熵值计算，最终得到480组数据。总数据中336组作为训练数据(占比70%)，144组作为测试数据(占比30%)。

从表1可以看出，超声解调信号在经过EMD分解与四类熵值相结合后对正常轴承、微损轴承、严重轴承三种特征状态均有良好的区分效果。而且，当对四类熵值进行特征融合后，其三种状态的准确率都有一定程度的提高，对于三种状态的平均识别率提高到99.31%，尤其对于微损轴承的监测准确率提高到97.92%，这对于区分轴承的早期故障有较好的效果。这也充分说明了利用多特征融合的故障识别方法提高轴承状态分类准确率的合理性。

最后，考虑分解后各分量的四类熵值曲线在第1～7层有着相似的变化规律，且通过经验无法有效判断哪类特征的评价效果最佳，因此针对此28维特征，代入随机森林获取不同特征对准确率的影响比例，28维特征在状态判别中的重要程度占比见表2。

表2 28维特征在状态判别中的重要程度占比Tab.2 Percentage of importance of 28-dimensional features in state discriminations %

由表2可知，多维特征值相融合后，各类特征熵值在7层分解中，近似熵对其三种状态准确率的判别效果最好，占比29.11%，第1层近似熵对轴承三种状态判断重要度最佳，达14.74%。同时随着分解层数的增加，对其判别重要性皆有一定程度的降低，结果表明通过这28维特征进行融合，对判断轴承的早期故障起到了良好的帮助效果。因此，多特征融合的方法可以提高轴承不同的状态识别准确率。

3 结论

本文基于轴承的超声解调信号，提出了一种经验模态分解后的本征模态分量与多类熵值结合的特征提取方法，并进行了仿真实验。实验结果表明，超声解调信号监测轴承早期故障有较高的识别准确率，其时频域在某种程度上可以有效反映轴承状态类别；对于各类状态识别，经过多特征融合后，相对于单一特征准确率更高；经EMD分解后第1层近似熵对其状态的区分效果最佳，可有效判断轴承早期故障，且各类熵值概念简单，计算也较便捷，因此为后期有效研究在线监测功能提供保障，可及时对现场故障类型得出精准判断，且可快速深入挖掘不同状态下的早期征兆，为有效地提供现场决策奠定科学基础。但由于数据量有限，因此信号特征和故障类别的物理机理还需要进一步研究和探索。